A brain？computer interface (BCI) is a non-muscular communication system that people can use to directly communicate their intentions from their brains to the environment [1,2]. The BCI system attaches a function to brain signals, thereby creating a new communication channel between the brain and external devices. This communication method is partially focused on the brain signal features extracted by the BCI system for device control and provides mutual interaction between the user and the system. Using different sensors and brain signals, many studies over the past two decades have evaluated the possibility that BCI systems could provide new augmentative technology without muscle control [3-8]. BCI systems have measured specific features of brain activity and translated them into device control commands. For example, an arbitrary limb movement changes the brain activity, such as electroencephalography (EEG), in the related cortex. In fact, even preparing to move and imaging a movement changes the so-called sensory rhythms. We can record α rhythm activity from sensorimotor areas, also called μ rhythm activity.

The decrease of oscillatory activity in a specific frequency band is called event-related desynchronization (ERD). Correspondingly, the increase of oscillatory activity in a specific frequency band is called event-related synchronization (ERS). The ERD/ERS patterns can be volitionally produced by motor imagery, which is the process of imagining the movement of a limb without actual movement [9]. In general, EEGs are recorded over primary sensorimotor cortical areas that often display 8？12 Hz (μ rhythm) and 18？26 Hz (β rhythm) activity. Several researchers have shown that people can learn to control the amplitude of μ/β rhythms in the absence of actual movement or sensation. Because μ/β rhythm changes are associated with normal motor/sensory function, they could be good signal features for BCI-based communication. Movement or preparation for movement, but typically not specific aspects of a movement such as its direction [10], are typically accompanied by a decrease in μ and β activity over the sensorimotor cortex, particularly contralateral to the movement. Furthermore, the changes in μ/β rhythms also occur with motor imagery. Because people can change these rhythms without engaging in actual movements, these rhythms could serve as the basis for a BCI system. To improve classification accuracy, in this study, a stochastic analysis-based method is employed for optimal feature selection and a linear regression classifier is applied.

This paper is organized as follows. In Section 2, we briefly describe related works for discriminant power feature selection, such as Laplacian spatial filter and principal component analysis (PCA). We explain the discriminant power feature selection method and motor imagery pattern classification method in Section 3. A motor imagery EEG classification experiment is introduced and the results are discussed in Section 4. Finally, in Section 5, we conclude this paper and suggest future works for improving our work.

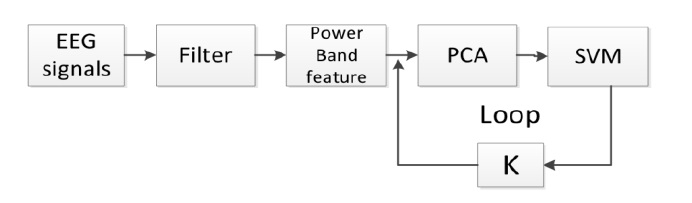
General EEG signal analysis in BCI systems consists of three major parts: preprocessing, feature extraction, and classification of the EEG mental tasks. In this study, the proposed method focuses on the feature extraction step. The initial procedure in feature extraction employs a spatial filter. The purpose of using a spatial filter is to reduce the effect of spatial blurring from the raw signals. Spatial blurring is an effect of the distance between the sensor and the signal sources in the brain and is caused by the inhomogeneities of the tissues between the brain areas. Several spatial filtering approaches have attempted to increase system fidelity. The most typical realization is a Laplacian filter, which consists of discretized approximations of the second-order spatial derivative of the two-dimensional Gaussian distribution on the scalp surface. A Laplacian filter attempts to invert the process that blurs the brain activities detected on the scalp. The approximations can be further simplified. For example, at each time point t, the weighted sum of the potential S_i of the four nearest or next-nearest electrodes are subtracted from the potential S_h at a center electrode for the small and large Laplacian, respectively.

Eq. (1) shows a description of the Laplacian filter. S_h and ？_h are the input and output of the EEG signal, respectively, corresponding to electrode h. S_i is the set of neighbor electrodes surrounding electrode h. Weight w_hi is a function of the distance between the electrode of interest h and its neighbor i, d_hi.

w_hi is the constant weight of the signal from electrode i of S_h, which could be calculated from Eq. (2), where d_hi is the Euclidean distance from electrode i to h. In practice, this filter is often implemented by simply subtracting the average of the four next-nearest neighbors (i.e., the weight for each neighbor is 0.25).

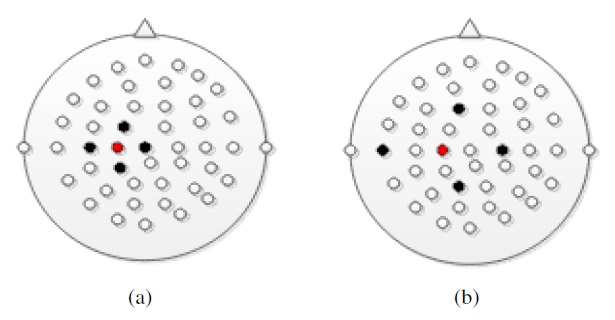
The main purpose of the spatial filter is to derive a more faithful representation of the sources within the brain and/or to remove the influence of the reference electrode from the signal. The influence is sensitive to the Laplacian mapping size as shown in Figure 1. In Figure 1 (a) and (b), the red and black dots indicate the location of the reference electrode and its spatial filter, respectively.

As described earlier, motor imagery has been shown to produce changes in the μ and β frequency band. EEG signals are filtered using a band pass filter, i.e., an finite impulse response (FIR) filter with a Hamming window for extracting the motor imageryrelated frequency bands (7？15 Hz and 18？22 Hz).

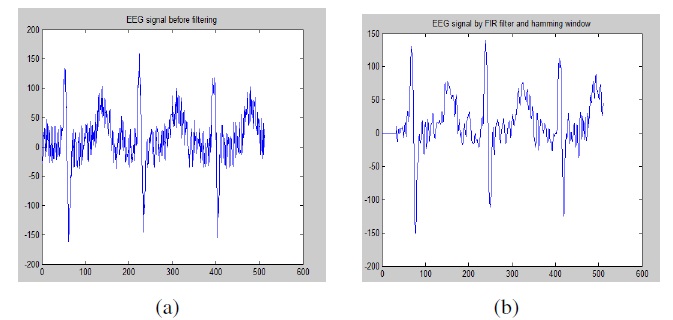
Figure 2 (a) shows raw EEG signals without the FIR filtering and Hamming window processing, while Figure 2 (b) shows the result of a filtered EEG signal by FIR filter.

The power bands are calculated from all electrodes of the extracted EEG with an epoch time of 1 second and a 0.5 second

delay from each epoch out of 4 second, during which human subjects start imagining a motor task (such as left/right hand or foot movement) and then finish it. We used 20% of the dataset as the testing set. The remaining 64% and 16% of the dataset were alternately used for training and validation.

Real-world data is often noisy because various signals from different perspectives are recorded and information is hidden in a few dimensions. PCA is a classical statistical method used to re-express the noisy data in a different framework. This linear transform has been widely used in data analysis and compression. PCA is based on the statistical representation of a random variable. Suppose that we have a random vector population,

where

and the population mean is denoted by

Mean subtraction from each data dimension is necessary for performing PCA to ensure that the first principal component describes the direction of maximum variance. If mean subtraction is not performed, the first principal component might instead correspond more or less to the mean of the data. A mean of zero is needed to find a basis that minimizes the mean square error (MSE) of the approximation of the data. The singular value decomposition (SVD) of

where the m × m matrix

is a matrix of the eigenvectors of the covariance matrix

matrix ∑ is an m × n rectangular diagonal matrix with nonnegative real numbers on the diagonal, and the n × n matrix

is a matrix of the eigenvectors of the covariance matrix

Under this condition, the principal component

of a dataset

can be defined as

With the first N ？ 1 components, the Nth component can be defined by subtracting the first N ？ 1 principal components from

as shown in Eq. (4):

We can achieve our goal of decorrelating the original dataset and reducing its dimension. Many methods exist for solving eigenvalues and corresponding eigenvectors, which is a nontrivial task. By ordering the eigenvectors in a descending order, we can create an ordered orthogonal basis with the first eigenvector (corresponding to the largest eigenvalue) having the direction of the largest variance of the data. In this way, we can find directions in which the dataset has the most significant amount among the multiple dimensions.

Our goal is to find a new matrix

which is a dimensionalityreduced random variable dataset, such that the covariance matrix

is a diagonal matrix, and each successive dimension in

is rank-ordered according to variance from the

Now, PCA allows us to find

It assumes an orthogonal matrix that acts as a transition matrix or function, as in

In this study, the motor imagery EEG signals are represented as

which were segmented from 1 second before the cue onset and 4 seconds after the cue onset of raw EEG signals for a total 5 seconds long time interval from 59 channels. The raw signals were sampled at 100 Hz, and they were spatially bandpassfiltered at 7？15 Hz and 18？22 Hz. We calculated a set of data that consists of a sample mean of

and a covariance matrix of

for each motor imagery state: {left/right hand, foot movement}. For PCA to work properly, we subtracted

from each data dimension in

This produced a dataset with a mean that is equal to zero.

Let

be a transition matrix that consists of eigenvectors of the covariance matrix as the row vectors. It is applied to reduce the dimensionality of

as shown in

Our goal is to find a matrix

The rows of

are the principal components of

Now, combining all the above information, we have

If

is orthogonally diagonalizable, it can be applied to the SVD such that

is a diagonal matrix and

is an orthogonal eigenvector that is diagonal to the symmetric matrix

Then, the ith column of

is the ith eigenvector of

Therefore, we can rewrite Eq. (5) as

In this case,

so that

By setting the principal components

equal to the eigenvectors

we can achieve dimensionality reduction.

The original vector

was projected on the coordinate axes defined by the orthogonal basis. It was then reconstructed by a linear combination of the orthogonal basis vectors. Instead of using all the eigenvectors of the covariance matrix, we may represent the data in terms of only a few basis vectors of the orthogonal basis. If we denote the matrix having K first eigenvectors as rows by

we can create a similar transformation. This means that we project the original data vector on the coordinate axes having dimension K and transform the vector by a linear combination of the basis vectors. This minimizes the MSE between the data and this representation with the given number of eigenvectors.

In this study, PCA was applied to reduce the dimensionality of the transformation matrix of the training set to

which is used to calculate the final feature using Eq. (8), where the transposed matrix of

has a dimension of k × N:

The output feature

is reduced to the k dimension (k ≤ N), which is determined by varying the number of k from 1 to N according to the arranged variance of the PCA in descending order of the training set to find the best model. The model that generates the best classification accuracy using a support vector machine (SVM) on the validation set is selected as the final model for the feature reduction method and applied to the testing set to test the proposed method.

The classification of the discriminant power feature is the most important step in analyzing motor imagery EEG signals. After we selected the optimal features as described in the previous section, we calculated the Euclidean distances between the motor imagery classes {left/right hand, foot movement} to apply them using a SVM.

In this study, the SVM algorithm is used by receiving input data during a training phase and shown good performance in classification phase. Thus, we built a classifier that could have been used to predict future data [11-13]. By using the SVM with dimensionality reduction, the system shows improved classification accuracy compared with previous approaches. To employ an SVM to classify the discriminant power feature of motor imagery EEGs, we must consider the following.

Given two-class training samples,

(x_i is the feature vector and m denotes the dimensionality of input space) and y_i ∈ {1, -1} denotes the class label of x_i. In the SVM training procedure, the optimal hyperplane has to be found, which can maximize the margin that separates the two-class samples. To minimize the problem, a convex quadratic program (QP) is commonly used.

We determined the Lagrange multipliers

that maximize the objective function, f(x):

where C is a positive constant specified by the user and K is a kernel function. In this study, we applied a Gaussian kernel function:

where σ is a constant specified by the user.

From Eq. (9), we can see that the size of the QP problem is equal to the number of training samples. SVMs are usually slow, especially for a large problem. Solving the above Lagrange multiplier, we can obtain the below decision function:

where b is a bias.

From Eq. (10), we know that 0 ≤ α_i^* ≤ C holds for i = 1, 2, . . . ,l. All the training samples are support vectors (SVs), and they correspond to α_i^* ？ 0. Let α_i^* ？ 0 for i = l_sv + 1, l_sv + 2, . . . , l. Thus, Eq. (12) could be rewritten as

In this study, we used the BCI competition III-dataset IVa in which five subjects (aa, al, av, aw, and ay) imagined a right hand and foot movement. We also used the BCI competition IV dataset I, which involved four subjects (a, b, f, and g); two of them imagined a right and left hand movement, and two others imagined a left hand movement and foot movement. BCI III contained 280 trials for each subject, and BCI IV contained 200 trials for each subject. All the datasets were normalized to 59 electrodes, and the epoch time was selected from 0？4 seconds, for which the stimuli was given to subjects at 0 second. The raw signals were segmented from 1 second before the cue onset (0 second) and 4 second after the cue onset, so in total, they

included 5 second long time intervals from 59 channels. As the result, the power feature of the original signal

can be regarded to have a dimension of [59 × 2 × 7].

Figure 3 illustrates the generalized process for discriminant feature selection with K dimensions and discrimination of the states of motor imagery EEGs. The original power features of

have a dimension of [59 × 2 × 7], so we have to find the dimensionality-reduced discriminant feature vector from them. K is the dimension of the discriminant feature vector for a new power orthogonal basis, so K is the dimension of the principal component of

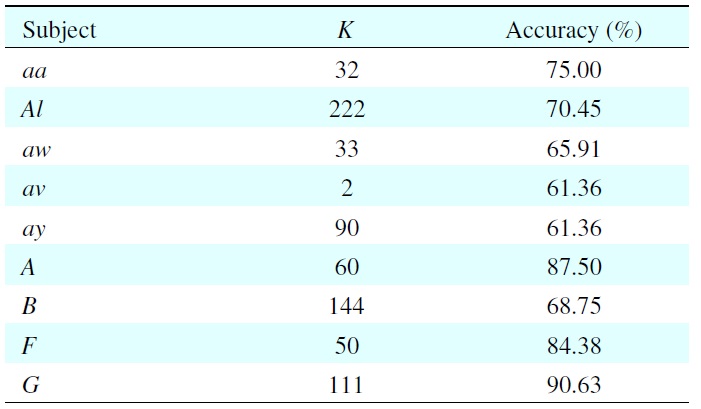
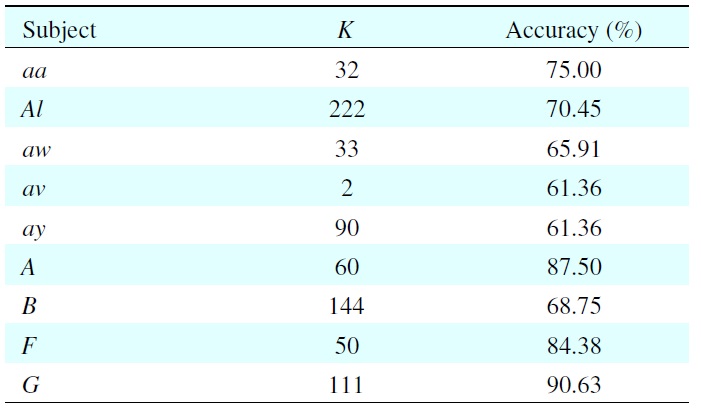
Table 1 shows the results of model selection of each subject with its best classification accuracy on the validation set. Because of individual differences, every subject has a different value of K. Thus, K is the number of components. In this case, we determine the accuracy rate of classification, p_acc, as follows:

For example, when subject aa has K = 32 based on the proposed discriminative feature extraction method, p_acc is 75%.

This means the 32nd dimension contains 75% of the total features. We can see that the EEGs are subject-dependent, and the value of K needed for each subject to obtain its best performance is naturally different for each subject. To compare the performance of our method with that of other approaches, we simulated state-of-art methods using the EEG feature extraction algorithm. First, we call type 1 the band power where all channels are the same, meaning all electrodes with average power have a 4s epoch. Type 2 is the method of extracting the band power feature based on the selected channels (C₃, C₄, C_z), which are related to motor imagery neuroscience studies.

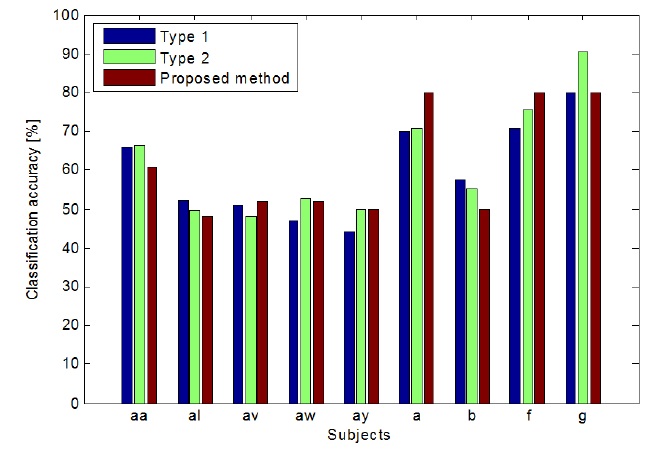
As shown in Figure 4, the proposed method outperformed the other methods. In case of type 1, it outperformed for subjects av, aw, ay, a, and f, and in the case of type 2, it outperformed for subjects al, ay, b, and g. The proposed method outperformed both the type 1 and type 2 methods.

To simplify the complexity of motor imagery EEG analysis in BCI systems, we proposed a discriminant feature selection method for motor imagery using an EEG-based BCI system. The proposed method is based on PCA and SVM. By applying PCA, we can successfully achieve our goal for discriminant feature selection, which is to decorrelate the original dataset of motor imagery EEGs and reduce its dimensionality while maintaining the discriminants. The selected features are in the form of a final feature vector set that we apply using a SVM as a classifier. By comparing the proposed method to previous methods, we found that the proposed method enhanced the availability of features up to 8% for each subject.

In the future, we will investigate other approaches for optimal feature selection without loss of performance. Although the proposed method improved the classification progress, the accuracy of the classification did not reach our goal. To improve the overall classification performance, we will study non-linear dynamical analysis approaches instead of stochastic analysis for brain signals.

No potential conflict of interest relevant to this article was reported.