Continuous efforts to put the Semantic Web vision into practice have led to two important insights: implementing a full-fledged machine understandable Web has largely failed, but focusing only on the ‘reasonable’ part already reveals a vast variety of valuable data [1]. This area of socalled linked open data (LOD) [2] has immediately spawned interesting efforts, like the DBpedia knowledge base (http://www.dbpedia.org/About) that currently describes more than 3.64 million things, out of which 1.83 million are classified in a consistent ontology. Moreover, the potential applications also promoted the development of innovative methods to make such data available to users in a structured way. Information retrieval (IR)-style or rule-based extraction frameworks, like ALICE [3], Xlog [4], or SOFIE [5], can already crawl the Web, and extract structured relationships from unstructured data with largely sufficient accuracy.
However, when it comes to retrieval of the now struc-tured information, the typical query paradigms also have to be adapted. This is not only because extracted knowledge is usually represented in some form of knowledge representation language (with resource description framework [RDF] triples as the most prominent example), but also due to the semantic loss of focus that results from ambiguities in the extraction process. For instance when querying for a person’s
While current retrieval paradigms, for example those in SOFIE’s retrieval engine NAGA [8] or Xlog’s DBLife [9], only focus on structured query language (SQL)-style retrieval (usually SPARQL over RDF) and keyword search with top-
In a nutshell, the problem is the intuitive interleaving of each individual user’s attribute value preferences, with the generally applicable preferences on attribute semantics, as specified in the query. Whereas skyline queries up to now only dealt with relaxing value preferences, the new additional relaxation in attribute semantics is owed to the linked open data. Let’s extend our example from above:
Example: A user might be interested in famous Nobel laureates in physics who were
To model this paradigm in databases (and schema malleability as such), each query attribute can be considered as a database column, holding not only tuples based on the strict relationships given by the query, but also tuples from semantic similar relationships. However, to prepare for later retrieval each such malleable attribute has to be associated with a second attribute measuring the semantic loss of focus for each tuple. This can be done by either automatically measuring semantic loss of focus by instance-based precision/recall tests, like shown in [10], testing the relationships’ semantic relatedness with externally available ontologies, like in [11], or simply denoting possible relationships, and allowing users to define a (partial) order over these relationships with respect to their queries.
In any case, the new associated attribute columns have to be considered by retrieval algorithms, but in contrast to the attribute value columns, have a slightly different quality. This is because relaxations on preferred
The contribution of this paper is threefold: we design an intuitive notion of skyline dominance with respect to malleability, in the form of semantically typed links in linked open data, and discuss its characteristics. We develop innovative algorithms to efficiently process skyline queries, even over large data repositories. And we extensively evaluate these algorithms with respect to runtime behavior and skyline manageability. In fact, our experiments show that in the general case, our algorithm can achieve significant performance improvements over the baseline. However, when slightly restricting general malleability, we can even show that performance can indeed be increased by several orders of magnitude, even rivaling the runtime behavior of classical skyline algorithms over strictly transitive preferences.
Please note that this paper is an extension of our work in [13]. Compared to [13], we heavily invest in generalized semantics for cases where non-malleable attributes show equivalent values. These semantics are discussed in Section IV-C and this new definition is also evaluated in Section V. This paper is structured as follows: after briefly surveying related work in Section II, we discuss the necessary foundations and theoretical characteristics of skylines over linked open data in Section III. Section IV then presents and evaluates skyline algorithms over several malleability attributes, whereas Section V deals with the special case of a single aggregated malleability attribute. We close with a short summary and outlook.
Due to its potential usefulness, linked open data has received a lot of attention, and even inspired a taskforce (http:// www.w3.org/wiki/SweoIG/TaskForces/CommunityProjects/ LinkingOpenData) of the World Wide Web Consortium (W3C). Current research is often focused on the area of business intelligence, but also for the collection of common knowledge. The basic idea is of using the Web to create typed links between data items from different sources. Once extracted, these links represent semantic relationships, which can in turn be exploited for querying. However, when querying (or reasoning over) such relationships, the exact nature of the relationship and its semantic correspondence to the query is often difficult. Therefore, apart from typical exact match queries (usually performed in SPARQL [http://www.w3.org/TR/rdfsparql- query/] over RDF triples), many approaches for ranking the best matching information have been designed.
The first notable approach to rank queries on extracted entity properties was Entity Search [14], proposing an elaborate ranking model that combines keywords and structured attributes. When it comes to also exploiting semantic relationships, NAGA [8] used a scoring model based on the principles of generative language models, from which measures such as confidence, informativeness, and compactness are derived, which are subsequently used to rank query results. Finally, [15] develops a general model for supporting approximate queries on graph-modeled data, with respect to both attribute values and semantic relationships, and derives a first top-
To our knowledge the only algorithm similar to skyline queries on linked open data is given by [17]. However, the developed algorithm has been designed for optimizing skyline queries over RDF data stored using a vertically partitioned schema model, and thus presents an efficient scheme to interleave the skyline operator with joins over multiple relational tables. Unfortunately, it does not offer any techniques with respect to personalization and the problem of semantic linkage, and thus is not really related to our work here. In brief, to our knowledge, our approach features the first skyline algorithm that respects semantic malleability.
III. THEORETICAL FOUNDATIONS OF MALLEABILITY-AWARE SKYLINES
In the following, we will briefly revisit the notion of Pareto skylines, as given by [18]. Assume a database relation
Assuming preferences
can be defined as:
Definition 1: Pareto dominance
The classical
Definition 2: Pareto skyline for some relation
Now we are ready to extend the semantics, by introducing the concept of
However, apart from the obvious scalability problems, the semantics are also unclear. Whereas attribute values, like dates, prices, or ratings, are usually crisp, and follow a certain preference order (users want the cheapest price for some product or the highest quality rating), labels for semantic relationships are usually fuzzy, and to some degree ambiguous, depending on their labels. Often
Definition 3:
A
It is easy to mix
Indeed, from an order-theoretical point of view it is easy to show that whenever
and
are given,
does not necessarily follow:
Lemma 1:
Proof: Transitivity for dominance regarding any product preference
and
can be constructed, for which holds:
but
Assume a product preference
and
such that
Now, assign values of
and
for attribute
Then, with respect to
holds because of
and
holds. However,
because of
but (
and
are incomparable with respect to
□
While the resulting preference orders are not transitive, at the same time domination relationships within the intransitive product order are sensible, since there can never exist any cyclic base preferences. However, this is only the case when strict partial-order preferences and
>
A. Implications for Algorithm Design
The danger of intransitivity of dominance relationships is that it may lead to
Example: When using non-transitive dominance with for instance a BNL algorithm, the result will vary
but
then a skyline computed by some BNL algorithm just contains
if the test for
is performed first, and thus
is immediately pruned from the database. Otherwise, if
is tested first, the resulting skyline contains
because
is removed prematurely, before
could also be removed by testing
and due to
incorrectly remains in the skyline set.
However, the idea of skylines is still sensible, since as we will prove in Lemma 2, cyclic preferences cannot occur, and thus a skyline based on the notion of containing all non-dominated objects can be computed. Since pruning may cause difficulties, the obvious way is by simply comparing all tuples in the database instance pairwise (with quadratic runtime). But, as we will see in the next section, far more efficient algorithms can be designed, and thus skylines over linked open data are indeed practical.
IV. MALLEABILITY-AWARE SKYLINES
Before delving into designing skyline algorithms capable of dealing with intransitivity, as described above, we have to formalize our concept of product orders also built from d-preferences in the form of a dominance criterion usable in skyline algorithms.
>
A. Malleability-Aware Skylines with Individual Attribute Malleability
Assuming preferences
can be defined as:
Definition 4: Malleability-aware dominance over individual attributes
In this definition, there is a malleability-aware dominance: 1) if all non-malleable attribute values of
show Pareto dominance over
and all malleable attributes of
are at least equivalent to those of
with respect to the
Lemma 2:
Proof: We have to show that the dominance relation of the product order does not induce cycles, more precisely, if
with
nor
is possible. Please note that
means
for all non-malleable attributes and
for all malleable attributes, i.e., no malleability is allowed for equivalence.
For 1 ≤
where the first
and therefore
and
impossible; 2) If there is no strict preference in the nonmalleable part, for all 1 ≤
is impossible. In the same way it is easy to also see that
is impossible.
□
Now, the respective malleability-aware skyline can be computed analogously to Definition 2, by:
Unfortunately, actually implementing such malleability- aware skyline computations algorithmically poses several challenges. Therefore, in the following we demonstrate how such algorithms can be designed. For the sake of cleaner notions and without loss of generality, we will assume that all our preferences are encoded in the database tuples by normalized scores in [0,1], where 1 represents the most preferable attribute values, and 0 the least preferable ones. Any database tuple
is given by
and the individual attributes can be separated into non-malleable data attributes
It is easy to see that this definition is equivalent to the Pareto dominance, as given by Definition 1, for the cases of
>
B. Computing Non-Transitive Skylines
As already indicated in Section III-A, modern Skyline algorithms have come to rely on the transitivity of dominance criteria. For the sake of improved performance, many tuple comparisons are avoided by pruning objects early, relying on transitivity for computational correctness, i.e., a tuple shown to be dominated can be fully excluded from further execution of the algorithm. However, without guaranteed transitivity, even basic algorithms like the well-known BNL algorithm [19] fail. Therefore, the need arises to develop new algorithms that are able to cope with these new requirements. In this section, we will therefore present a general purpose algorithm designed for use with any non-transitive dominance criteria, including dominance for malleability-aware skylines.
The naive solution to the given problem is relying on exhaustive pairwise comparison, i.e., each possible tuple pair has to be tested for dominance. However, this algorithm shows prohibitive practical performance, requiring 1/2(
Hence, we propose a novel algorithm, which is capable of dealing with any transitive or non-transitive preferences
Given is a database relation
[Table.10] Algorithm 1 Non-transitive skyline algorithm

Algorithm 1 Non-transitive skyline algorithm
The algorithm contains two loops, the outer one iterating
Furthermore, this algorithm can be efficiently implemented by representing the membership of a tuple in the different sets by simple flags attached to the tuples in
>
C. Expanding Semantics for the Case of Equivalent Data Attributes
In the following, we will introduce a more general definition of malleability-aware skyline semantics, addressing some restrictions of the semantics introduced in Definition 4. Especially, we focus on the case that all non-malleable attributes are equivalent, i.e.,
For the case of equivalent data values, in our initial definition, we demanded strict dominance with respect to malleable attributes, in order to establish a dominance relationship between the two tuples. This constraint does not capture the intended semantics of malleable skylines perfectly, as it allows for no vagueness in the case of equivalent data values. However, Definition 4 represents a pragmatic restriction for the sake of simplicity, and guarantees the absence of cycles without any additional effort. For many datasets, i.e., especially those that have large, or even continuous domains for the non-malleable data attributes, this restriction has a negligible impact, as tuples with equivalent data attributes rarely occur. However, for tuples with smaller attribute domains, tuples equivalent with respect to data attributes may happen frequently, and thus, often, our malleable skyline heuristic does not trigger.
Therefore, the definition presented in the following will expand on this case, also allowing soft-dominance when non-malleable attributes are equivalent, but resulting in a more complex and computation-heavy definition. The effectiveness of this modification is highly dependent on the current dataset, and especially shines in scenarios where data equivalences can frequently occur― e.g., e-commerce datasets where product facts are automatically extracted from the Web, resulting in varying extraction quality (malleable attributes), and often colliding data values (as there is a common consensus among most manufacturers with respect to which product properties make sense and which don’t).
Let
where the first
is defined analogously.
Then, similar to Definition 4, we can define general malleability-aware dominance between two tuples
as
Definition 5: Malleability-aware dominance over individual attributes
We will discuss the detailed semantics of this definition in the following:
Part (2) of Definition 5 is similar to Definition 4, and encodes the semantic that if all non-malleable attribute values of
show Pareto dominance over
and all malleable attributes of
are at least equivalent to those of
with respect to the
Also, the next two parts (3) and (4) also directly correspond to Definition 4. Please note that we changed the notation, in order to be consistent with the later components (5) and (6) of the definition, i.e., the expression
as used in Definition 4 is equivalent to
as used by (4) in Definition 5. Therefore, this part still means that if no soft
The extension of Definition 5 over Definition 4 is in (5) and (6): here, an additional alternative option for establishing dominance is provided for the case that the non-malleable attributes are equivalent. Therefore, this new definition is more general, and it will usually result in more dominance relationships than the previous Definition 4, i.e., the resulting skyline is either equal, or a strict subset of a respective skyline, in accordance with Definition 4.
The semantics of (5) and (6) are that for the case
it is also possible to use soft-dominance on malleable attributes, as long as certain restrictions hold: especially, (5) encodes that tiny value variations within malleable attributes smaller than
are considered as just being noise, and only larger variations of
can lead to a dominance relationship between
and
Unfortunately, this change breaks the guaranteed absence of cycles, one of the major features of the original Definition 4. Therefore, further restrictions are needed, in order make use of both soft-dominance for malleable attributes, and cycle-free dominance relations. These restriction are given by (6), i.e., by the additional constraint
This constraint describes that in order for
to dominate
needs to be better in its sum over of its malleable attributes. This enforces a compensation mechanism, i.e., in order to dominate; a tuple
has to show at least one malleable attribute for which it is significantly better than the respective attribute in
and all other malleable attribute values that are worse in
than in
(but still below the noise level) need to be compensated for by the entirety of the tuple. Therefore, for example, dominance between an overall inferior tuple (but with all inferior malleable attribute values being below the noise threshold) showing just few better values is disallowed, unless the better values are significantly better, also compensating for the shortcomings of the other attributes. This eliminates the source for cyclic dominance relationships, rendering this definition safe.
>
A. Evaluating General Malleability-Aware Skylines
In this section, we evaluate the effects of malleabilityaware dominance, respecting any number of malleable attributes on the properties of skylines. Furthermore, we will also measure the performance of respective skyline algorithms.
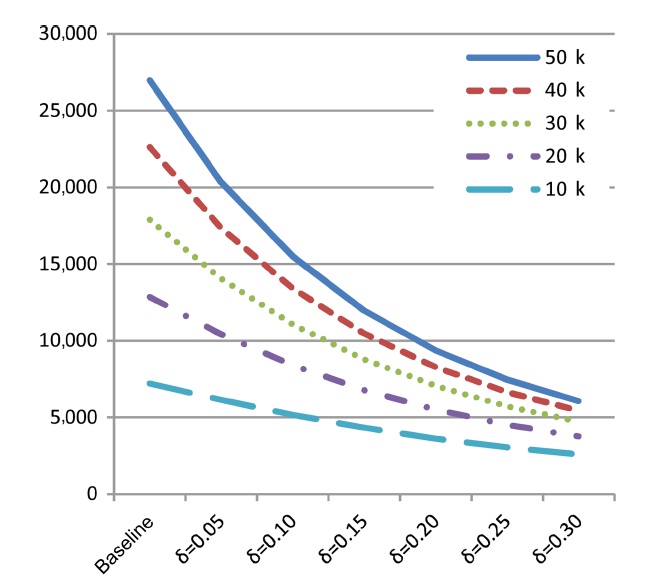
1) Skyline Size
For the first set of experiments, we examined the impact of malleability-aware dominance (represented by varying values
ensure comparability, the same random seed is used for each
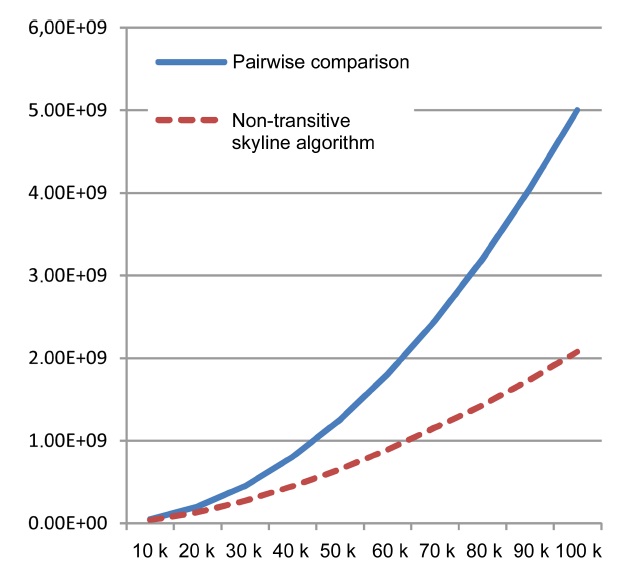
2) Performance of Algorithms
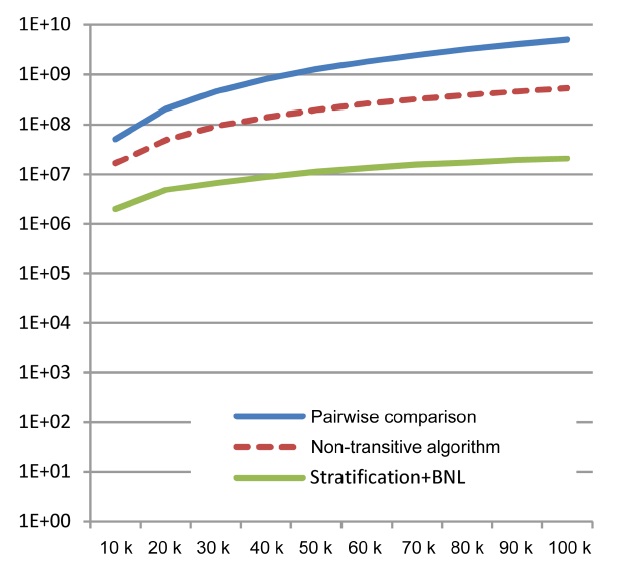
In the second set of experiments, we examined the performance of the naive baseline and our non-transitive skyline algorithm (measured in the required number of tests for dominance). Similar to the last experiment, we again relied on synthetic data with 12 independentattributes (6 malleable, 6 non-malleable), and incrementally increased the size
and just a single core.) Therefore, additional optimizations must be found for application domains with tighter time constraints.
>
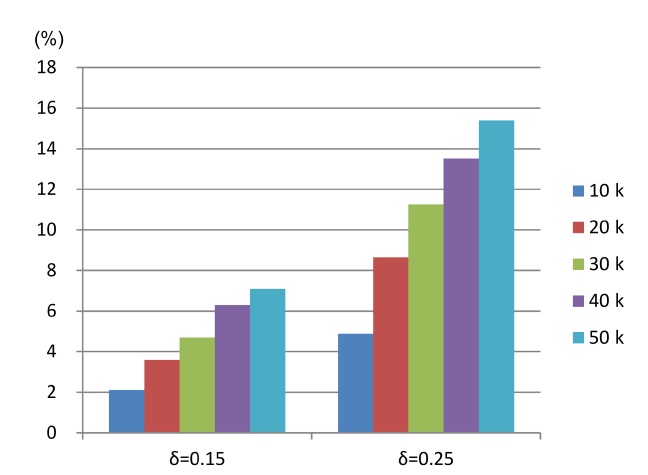
B. Effects of General Semantics for Equivalent Values
In this section, we briefly demonstrate the effect on the skyline size of the alternative Definition 5 for malleable skylines, given in Section IV-C, over the original Definition 4, given in Section IV-A. As this definition specifically extends Definition 4 with respect to equivalent (nonmalleable) data values, this experiment uses slightly different data sets, encouraging the occurrence of such tuples (i.e., showing equivalent non-malleable parts). This is achieved by generating discrete data values with 10 levels, e.g., possible values are 0.0, 0.1, …, 0.9. Furthermore, we only use 5 non-malleable attributes and 5 malleable ones, for a total of 10 attributes. Skylines computed using definition 5 are, as mentioned in Section IV-C, a subset of skylines computed with Definition 4, i.e., Definition 5 may result in additional domination relationships under certain conditions (simplified: when non-malleable attributes between two tuples are equivalent, and the malleable attributes are not strictly dominating, but most non-malleable attributes are roughly similar, with some attribute values being significantly better for one tuple).
In brief, in this experiment, we measure the
{0.15, 0.2}, and
>
C. Malleability-Aware Skylines with a Single Malleable Attribute
As demonstrated in the last section, the runtime of general non-transitive skyline algorithms with one malleable loss-of-focus attribute for each non-malleable data attribute can be quite high. Thus, for time-critical applications, we suggest reducing the number of malleable attributes to using just a single attribute. This single attribute then represents the overall loss-of-focus of a given database tuple with respect to the query, in an aggregated form. This reduction can be implemented by different methods: 1) by combining multiple malleable attributes by some combining function, or 2) by directly eliciting just a single attribute representing loss-of-focus, using one of the established frameworks for this task (e.g., [10] or [11]).
As an immediate effect, the number of dimensions to be respected during skyline computation is reduced drastically, leading to direct performance advantages, due to respectively reduced skyline sizes. However, there is a less obvious and significantly more crucial advantage resulting from this reduction, which allows us to build vastly more efficient skyline algorithms. The basic considerations leading to these algorithms are as follows:
When using established skyline algorithms, like BNL, the only problem which is encountered when dealing with malleability-aware dominance is that tuples are eliminated early that are required to dominate another non-skyline tuple, and due to non-transitivity, none of the remaining tuples can lead to the same dominance; thus an incorrect skyline is computed (e.g., see example in Section III-A). Therefore, we could use a more efficient standard algorithm, like BNL, if it could be made “safe”, i.e., if this situation can be prevented. In the general case with multiple malleable attributes, this is unfortunately not possible. But when using just one malleable attribute, the correctness of BNL depends only on the order in which the tuples are inserted into the window: for example, consider three tuples with preferences already encoded in scores
and
the bold score represents the single malleable attribute. When computing a malleability-aware skyline with
and the resulting skyline is just
But due to
the BNL algorithm could first test
removing
and resulting in the skyline
(because
cannot be dominated anymore). Obviously, the skyline result would be correct, if the tested order was
It is easy to see that this observation can be generalized, i.e., problems in BNL can only occur if tuples with a lower malleability score are removed before they have been tested for dominance against all tuples with a higher malleability score. Therefore, for the case that there is only one malleable attribute, we can use established algorithms like BNL, if all tuples are processed in descending order with respect to the malleability attribute (preventing the situation leading to incorrect skylines described above), i.e., the skyline algorithm is therefore
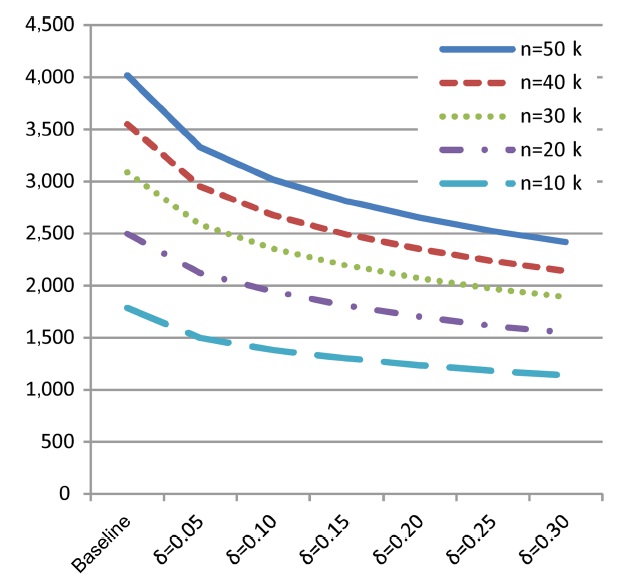
1) Skyline Size
Before dealing with performance issues, similar to the last section, we also measured the skyline sizes for varying
2) Performance of Algorithms
In this last set of experiments, we examined the performance of the naive baseline, our non-transitive skyline algorithm, and the stratified BNL algorithm as described above. Again, performance is measured by the required number of tests for dominance. We also relied on synthetic data with 7 independent-attributes (one malleable, 6 non-malleable), and incrementally increased the size
In this paper we discussed the case of query processing over LOD. Whereas traditional query processing algorithms are usually graph-based, and use exact matches on typed links between data items in SQL-like languages like SPARQL, the fuzzy nature of semantic links calls for approximate query processing algorithms. In particular, the exact labels of links cannot always be taken at face value, because information extraction techniques, the use of different concept ontologies, and slight variations in the links’ semantics introduce quite a bit of fuzziness, which algorithms have to deal with. Relying on techniques to estimate different labels’ loss of focus regarding each other, in this paper we presented the first skyline query algorithm that can efficiently deal with semantically typed links in linked open data. Modeling the semantic malleability of attributes by d-preferences, we proved that the resulting product order is indeed well defined, and can be used effectively as the basis for a sensible definition of malleability-aware skylines over linked open data.
Moreover, in our experiments we show that our innovative algorithms can efficiently evaluate such skylines, and when restricting the type of malleability, will even result in runtime improvements of several orders of magnitude against the baseline. Therefore, even interactive applications with tight response time requirements are possible. While we performed the algorithmic considerations here on synthetic data to test our algorithms in an unbiased environment, our future work will focus on the integration of our algorithmic framework into practical LOD sets. Our aim is to use potential bias in the data for a tighter integration of the attribute malleability, respective to each individual query. It seems that different query intentions might need different degrees of admissible malleability, to stay semantically meaningful.