A true random number generator (TRNG) is used for cryptography technology as a seed or nonce information. Therefore, a cryptography module should include a generator for cryptographic applications. Traditionally, an analog circuit is used for the generator, but it occupies a large area on the chip. Recently, research on a digital true random number generator has been introduced. The method uses the non-deterministic state in a digital circuit.

The non-deterministic state called metastability is a good source of randomness. For this reason, research on producing a digital random number generator by inducing metastability has been conducted [1-3]. By adjusting the programmable delay line, setup and hold time violations happen and the digital circuit generates random numbers.

Recently at the Workshop on Cryptographic Hardware and Embedded Systems 2011 (CHES 2011), a proportional integral (PI) controller-based TRNG was proposed [4]. The method induces a metastable state by using feedback information. The straightforward implementation of the design seems flawless but the random numbers are skewed and biased because the PI controller rarely forces the circuit into a metastable state. To eliminate deterministic values, a filtering system was introduced which removes signals which are replaced in outside of the metastable state by calculating the proportion of the output and determining the random number.

The method ensures high entropy by removing the deterministic state but its throughput decreases to half of the whole throughput because the non-deterministic state occupies half of the throughput. Therefore, we need to find the way to improve the original throughput.

In this paper, we propose high randomness with original throughput by using a novel always metastable state method. The method ensures the original throughput after conducting filtering to improve randomness.

The paper consists of four sections. In Section II, we introduce our main idea, a novel random number generator. In Section III, we evaluate the performance of the proposed method, and then in the last section we conclude the paper.

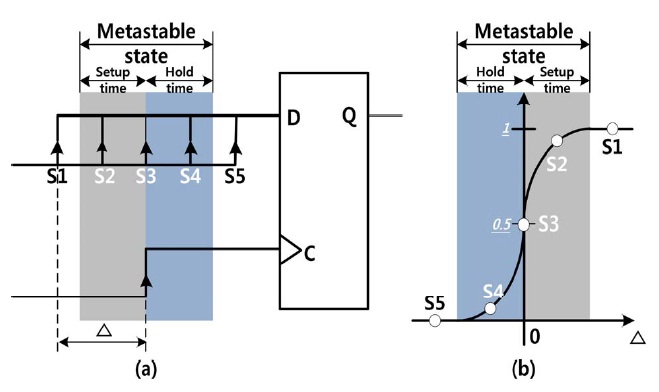
A random number generator produces random numbers based on high entropy sources including thermal sources, shot noise in circuits, nuclear decay, and metastability. In digital circuits, utilizing analog sources guarantees unpredictable random numbers. However, such a circuit occupies a huge chip area. Considering cost and effect, the metastability-based digital circuit is one of the finest solutions. Metastability is an uncertain and unpredictable state. In Fig. 1, the features of metastability are depicted. While in the signal transition period, the signal should be maintained for the setup and hold time. If the condition does not meet the requirement, the uncertain state occurs and the results are unpredictable. Therefore, inducing metastability generates random numbers.

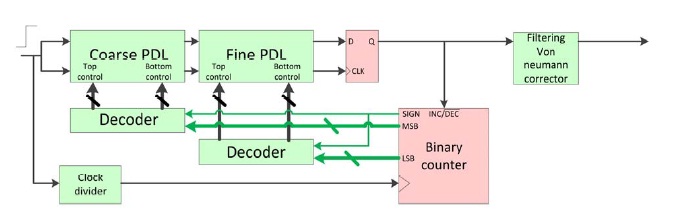
Traditionally, jittering of circuit has been used to generate metastability. Recently, a metastability-based TRNG was proposed by [4] in which the programmable delay line and feedback control logic is applied to a TRNG. The details information is are shown in Fig. 2.

The logic consists of three parts. The first part is the propositional dynamic logic (PDL), which controls the delay by altering the propagation line. Coarse PDL and fine PDL generate long and short delays, respectively. After generating random sequences, the output processes the filtering and von Neumann corrector to eliminate bias and skewed data. At that time, the output is sent to the binary counter, which controls the length of delay by imposing the signal to the PDL logic.

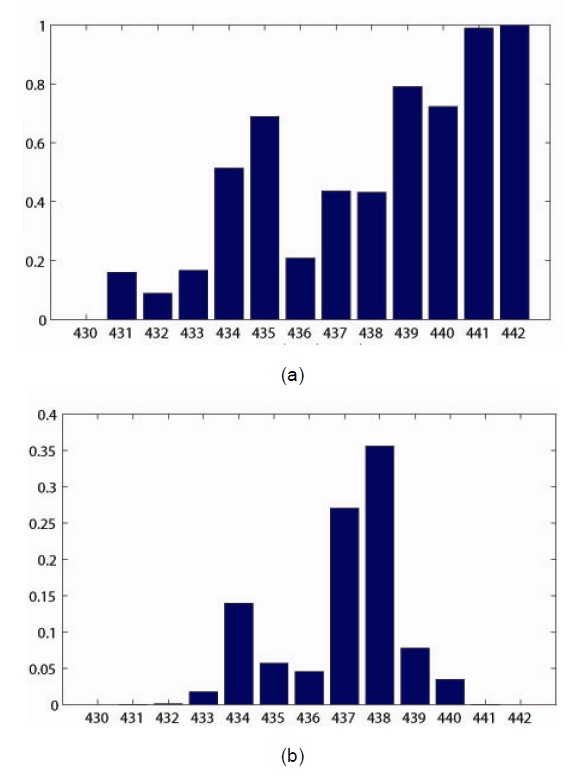
However, the method has a disadvantage from using the filtering system. After generating the output with PDL tuning, the results are skewed, so the information cannot be used for random numbers. To solve the problem, a previous paper used a filtering system that first analyzes the random number range and then outputs values in the random number range. Finally, it reduces the throughput to half of the original throughput. Fig. 3 provides more details: Fig. 3a describes the proportion of the output, one or zero. When the value shows a 50% one and zero output, that state is metastability. In Fig. 3b, the occurrence of counter “ 437” and “ 438” is the highest in the graph. This means metastability is generated at a high rate in the designed circuit. However, half of the values are outside the range of metastability. Therefore, a filtering system improves randomness by removing the deterministic state, but throughput decreases as well. In this paper, in order to preserve the high throughput, we present a novel method, the always metastable state method. The method does not output deterministic values and the original throughput is maintained.

In the filtering system, we implemented storage for the result of the metastable output. The space accumulates the values and outputs the values while the TRNG indicates a metastable state. The value is stored until the number of outputs reaches the maximum size of the storage. When the number exceeds the limitation, the last value is abandoned.

In case of a non-metastable state, the output is blocked and the value is replaced with a value from the storage indicating metastability. After outputting a random number, the value is rotated into the starting address of the storage. The feature can contribute to randomness by mixing the metastable storage by rotating the metastable value. It can also maintain a reference of metastable values.

As a result, even during the non-metastable state we can enjoy access to metastability values and also maintain the original throughput.

To determine the metastable state, the previous method collected outputs and calculated the proportion of zeros and ones and then sought the value from the metastable state that generated an equal number of outputs, one and zero, and had a high occurrence during random number generation.

However, our method uses a real-time evaluation system. Whenever the original output is inserted into the filtering system, we first accumulate the values in the queue storage. Then we analyze the proportion of ones and zeros. This is the basic randomness test in the National Institute of Standards and Technology (NIST) [5] and DIEHARD test suite [6]. The value which shows high randomness in the test is determined to be generated from a metastable state.

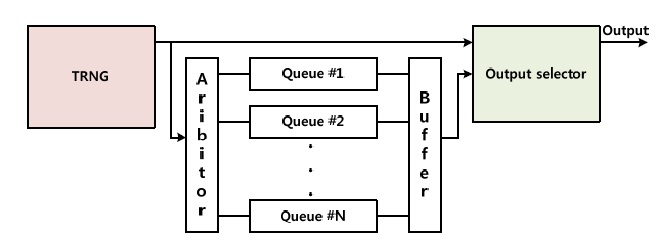
Fig. 4 shows the design of the whole design and filtering system. The filtering system is located after the TRNG module.

Fig. 5 shows the source code of the algorithm. The inputs are “ counter” which indicates a state counter, and “ value” which indicates an output value. After conducting an operation, a random value is generated. In step 1, the value is queued to storage at the address which is indicated by its state counter. In step 2 and 3, we checked the metastablity by calculating the proportion. To find metastability, the total value of the indicated queue is computed and the value is divided by the size of the queue. The result is reduced by 0.5 and then the value goes through an absolute operation. If the value is close to 0 that means it has high randomness. The HM operation finds the highest metastable state by searching through the all of the results of the randomness test. In step 4, the algorithm compares the counter with the highest metastable counter. If the counter indicates high metastablity, it will be used for output in step 5. Otherwise, the value from highest metastable storage will be outputted and then the storage will be rotated in step 7 and 8. Finally, in step 9, a random value is outputted.

Since the previous method includes outputs from a nonmetastable state, the original outputs from the previous design are skewed and biased. To solve this problem, the previous method in [4] filters out about 50% of the whole throughput. Even though the randomness increases, the throughput decreases. In the proposed method, we always output metastable values by using a novel filtering system. The filtering system does not reduce the throughput, because the stored value from metastability replace the deterministic value with a high entropy value. Through the technique, the throughput is maintained and randomness is also maintained. More detailed information is depicted in Table 1.

Our method does not show reduction of throughput even after filtering. However, the previous filtering method shows a high reduction of throughput by filtering out the deterministic values. In the experiments, we evaluate four scenarios. In the first one, no filtering method is conducted. In that case the TRNG achieves high throughput but does not generate random numbers. Secondly, we used just one metastable value. In that case, randomness is high but throughput is only 24% of all values generated. When we gather three metastable state values, it shows reasonable throughput but it is still just 63%. The final experiment is gathering three metastable values and two deterministic values. In that case, throughput is high but randomness is not shown. Therefore, the previous method has a trade-off between randomness and throughput. However, our method does not have that trade-off, so we can achieve throughput together with randomness.

This paper presents a novel approach to TRNG for high randomness with the original level of throughput. The method successfully generates output from a metastable state even under a deterministic state by using storage for accumulating random numbers from the metastable state. Therefore, the method does not influence the randomness and it even shows the original throughput. The technique is a filtering system, so it can be used for any traditional kind of metastable based TRNG as a post-processing method. This shows the high flexibility of the proposed method. The method is evaluated by using a software version, so our future work will involve implementing the method in hardware design with a small chip area while achieving high throughput as well.

In Fig. 6, when the TRNG outputs a value, the value goes to two paths, one for the output selector and one for the queue storage. If it is a value in the metastable state, the value is directly outputted by storing the value into the metastable queue. Otherwise, if the value is in a non-metastable state, the value is stored into a designated address and a value is outputted from the metastable queue.

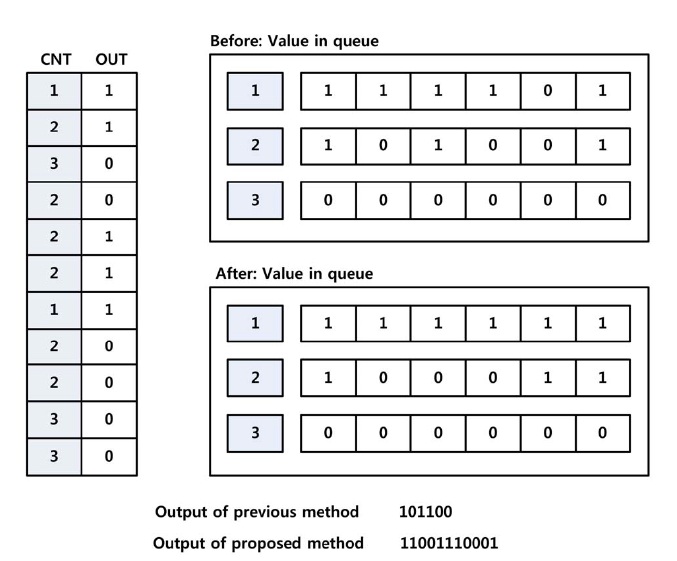
In Fig. 7, the left figure presents output values in order. The right two figures show before and after images of the storage value in each queue. Below, the result of output shows that the proposed method has twice as high a throughput as the previous method.