Over the last few decades, a considerable number of modern homing missile guidance laws have been proposed. Optimal control and sliding-mode control theories have been widely used to derive modern guidance laws with improved performance. Most optimal guidance laws (OGLs) have been derived from the linearized kinematic model based on the linear-quadratic optimal control theory to obtain feedbackform solutions. Closed-form OGL has been derived for missiles with time-varying velocity [1] and for internal dynamics with an uncertain time lag [2]. OGL and nonlinear estimation for interception of the decelerating target [3] and accelerating target [4] have been discussed for a highly maneuvering target with various scenarios. Optimal guidance with bias error in estimation of time-to-go [5] and OGLs subject to various final constraints have been studied in [6-7]. An optimal midcourse fixed-interval guidance law without velocity constraints has been developed for intercepting a target with a constant acceleration vector in [8]. An extensive literature review on guidance laws and OGLs have been performed in [9-10].
Although the optimal control system is accurate and economic in energy consumption, its behavior could be deteriorated by uncertainties such as parameter variations and external disturbances, the system performance criterion will be deviated from the desired values, and even the system may become unstable. In optimal guidance laws for moving targets, because of the guidance law’s dependence on the information of relative range, relative velocity, and even the target’s future acceleration, its implementation is difficult. The optimal control theory in missile guidance assumes that the maneuver strategy of the target in the future is entirely identified, so any small changes in the target’s acceleration produce undesired results.
On the other hand, sliding-mode control has been widely recognized as a powerful control strategy for nonlinear systems, such as missile guidance, due to its ability of making a control system very robust in the face of modeling imprecision. The main advantage of sliding-mode control is that the system’s response remains insensitive to model disturbances and uncertainties [11-12]. A sliding-mode control law has been developed for an air-to-air missile considering nonlinear engagement [13]. It has been proven that the performance of the feedback controller is robust to certain parameter variations in the model by assuming that the maximum target’s acceleration is known in advance. Reference [14] has designed an adaptive-sliding-mode guidance law for missiles equipped with thrust vector control using adaptive control and sliding-mode control to minimize the distance between the centre of the intercepting missile and that of the target missile asymptotically. In [15] a passive homing guidance law has been proposed for a stationary or a slowly moving target using the sliding mode control technique.
A typical sliding-mode controller (SMC) is conventionally designed for the worst cases in which system uncertainties and disturbances are considered. In such circumstances, stability and convergence are the main purpose of SMC. However, when the system nominal part is dominant, robustness is not the only concern in the control design and other performances should be also taken into consideration. An interesting question here is, while retaining the system stability of SMC, whether we can consider other performance indices, such as minimizing input energy, achieving faster tracking convergence, etc in the control design. The answer is Yes.
Integrating optimal control with the sliding-mode in missile guidance allows the interceptor to achieve optimal performance and compensate for inaccurate predictions of target maneuvers and unmodeled dynamics. The guidance law based on the integration of the sliding-mode and optimal control theories has been proposed for a homingmissile against a maneuverable target in [16] and for the fixed interval guidance law without velocity constraint in [17]. In [18] by integrating optimal and sliding-mode theories, a guidance law has been derived for the terminal velocity constraint as well as the terminal position constraint to achieve robustness against disturbances and terminal accuracy for fixed-interval propulsive maneuvers.
This work deals with integrating optimal guidance with the sliding-mode control theory for a surface-to-air missile in a 3-dimensional space to obtain a new guidance law with good dynamic performance, energy saving properties, terminal accuracy and robustness against disturbances such as the target’s maneuvers. The control method based on SDRE is one of the recently proposed nonlinear control methods [19]. The SDRE control technique reformulates a nonlinear dynamic equation into state-dependent coefficient (SDC) form and solves a Riccati equation as in the LQR control technique. The adoption of SDRE to control nonlinear systems has been increasing due to its promising real time performance and flexible design. Through extensive simulations, the SDRE method has demonstrated its effectiveness as a method for designing nonlinear controllers, observers, and filters [20-21].
To achieve optimal performance and reject the disturbances for the nonlinear system, a SDRE incorporated with the sliding-mode control technique in order to derive a missile guidance law is considered in this paper. This control strategy not only causes optimal performance to be achieved but also guarantees robustness. The simulation results verify the effectiveness and robustness of the proposed guidance law.
This paper is organized as follows: Section 2 presents the mathematical model of the guidance system. Section 3 formulates optimal problems incorporated with slidingmode control. The optimal control problem based on the SDRE method without regarding uncertainty is explained in Section 4. In Section 5, the optimal sliding-mode guidance (OSMG) is designed. A simulation example is given in Section 6 to confirm the guidance performance. Finally, conclusions are provided in Section 7.
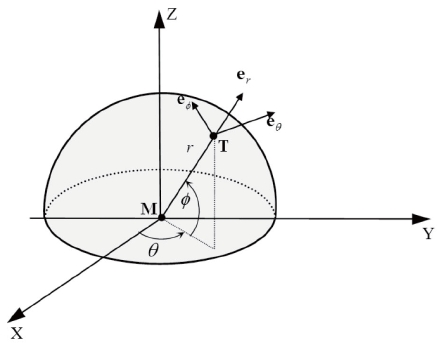
Figure 1 shows the three dimensional pursuit geometry within the spherical coordinates system (
The missile and target are assumed to be point masses in
order to easily analyze the missile guidance. Suppose (e
Differentiating both sides of the above equation yields the components of the relative acceleration as follows:
where
and
are tangential relative velocities, the kinematics (2) can be rewritten as the following standard nonlinear state space equations:
where the state vector x
Consider an uncertain affine nonlinear system described by
where x(
According to the mentioned assumptions, the system (4) can be rewritten as
Another assumption is regarded as follows where
In system (7), assume that u=u
where the weighting matrices Q(x)∈R
where u
4. Optimal Control Design Based On the SDRE Technique
Introduced by Cloutier [22] for the first time, the SDRE control method reformulates a nonlinear dynamic equation into SDC form and solves a Riccati equation as in the LQR control technique. It is completely similar to the LQR technique in terms of the compromise between the control inputs and state errors. Also, the SDRE control technique has good robustness properties like the LQR. In the current section, by using the SDRE method, a suboptimal control law is derived for the nonlinear system (7). Using direct parameterization of f(x)=A(x)x and g(x)=B(x), the nonlinear equation (7) can be transformed to the SDC form as follows:
Apparently, the choice of the matrix A(x) is not unique and this may lead to a suboptimal controller [22]. This method requires that the pair {A(x), B(x)} is point wise controllable. The optimization problem is to find the control u
where P(x) is unique, symmetric, positive-definite, and is computed from the solution of the state-dependent algebraic Riccati equation:
The SDRE solution to the infinite-time nonlinear regulator problem (7) and (8) is, therefore, a true generalization of the infinite-time time-invariant LQR problem, where all of the coefficient matrices are state-dependent. At each instant, the method treats the SDC matrices as being constant, and computes a control action by solving an LQ optimal control problem. Cloutier [22] has shown that this control law is locally stable and optimal with respect to the infinite time performance index. Moreover, he has given the conditions whereby the SDRE control law can be globally stable and globally optimal.
5. Optimal Sliding-Mode Control
5.1 Design of the Robust Optimal Sliding Surface
The integral sliding surface for the optimal sliding-mode method is defined as follows:
where G(x)∈R
?=G(x)[?(τ)-A(x)x(τ)+B(x)R(x)-1B(x)
?=G(x)[A(x)x(
?=G(x)B(x)[u(
If we apply ?=0 we can find the control input vector as follows:
u
Compared with the control input in the SDRE method (11), it can be easily seen that they are the same. Thus, by choosing the above mentioned switching surface, we achieve a control law that is not only robust but optimal also.
The SMC law is obtained such that it satisfies the reaching condition
provided that
where
where ?s?1 represents 1-norm. Because of ?s?<?s?1, we can get the fact that
5.2 Design of Switching Surface and Matrix
In this section, an optimal sliding-mode guidance law is designed for a missile in 3-dimensional space. The final and most important element remaining in our design is to choose two main parameters. These parameters are switching surface and the matrix G(x). The switching surface is defined as follows:
where
Then we have,
Matrix G(x) is not unique. To obtain G(x) from (24), the very important assumption of non-singularity of G(x)B(x) should be considered and then it is obtained as follows:
where
In this Section, a numerical simulation is presented to justify the use of our proposed method. Here, a sliding-mode guidance law with a switching surface like that considered for the optimal sliding-mode guidance design is also designed. Engagement performance and robustness of the proposed optimal sliding-mode guidance, sliding-mode guidance, and the well known APNG [23] laws against different types of targets and for some different scenarios are compared. The external disturbance in (3) is generated by the following types of different target maneuvers in order to test the robustness in this example.
ramp target
w=
sinusoidal target
w=sin(Ω
where
Case 1: Target is moving toward the missile (wr<0)
r=10km , θ=π/3 , ?=π/3 , vr= ?1000m/s , vθ=200m/s , v?=300m/s
Case 2: Target escapes from the missile (wr>0)
r=4km , θ=π/3 , ?=π/3 , vr= ?500m/s , vθ=200m/s , v?=300m/s
In OSMG law, weighting matrices Q and R are chosen as follows:
where
The fourth-order Runge?Kutta algorithm is used to obtain the numerical solution of the target and missile motion equation. The guidance command is given out by a microcomputer onboard the interceptor and the sampling period is assumed to be 5 ms. The following provides discussion on the simulations.
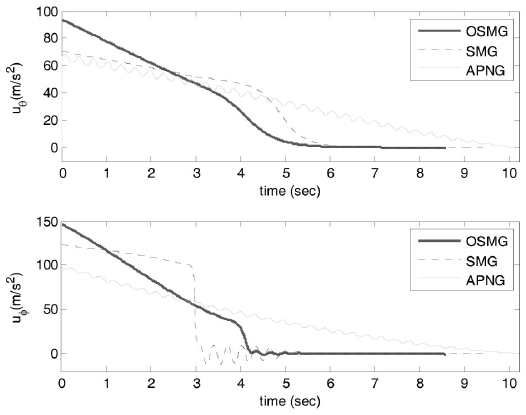
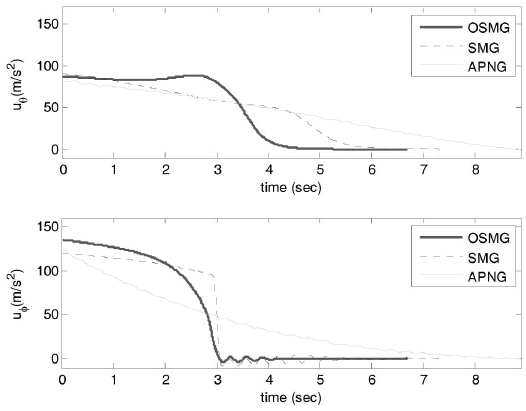
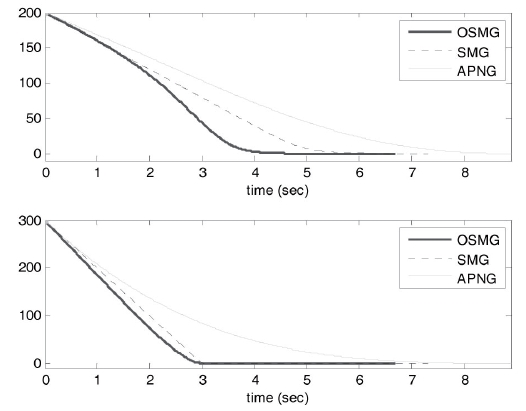
Comparisons of control inputs between OSMG, SMG and APNG laws for the sinusoidal target are discussed. Control commands for three guidance laws and for both cases 1 and 2 are shown, respectively, in Figs. 2 and 3. Figure 2 illustrates the simulation result with the initial condition of case 1, in which the target is moving toward the missile. Fig. 3 illustrates the simulation result with the initial condition of case 2, in which the target escapes from the missile.
For control inputs, fuel consumption which is an important specification is compared. For both cases 1 and 2 we see that the fuel consumptions in the OSMG design are
all much smaller than those of the APNG law. Compared with the SMG law, the OSMG law has slightly less fuel consumption. So, concerning fuel consumption, the OSMG law yields better results. This is due to the fact that the control energy consumption has been included in the designed performance index. On the other hand, control inputs in the OSMG law are smoother than that in the APNG law for both cases. This is because the APNG law is a function of instant target acceleration but OSMG is not. Also, because some coefficients in the SMG law are chosen such that it consumes less energy, it exhibits little chattering.
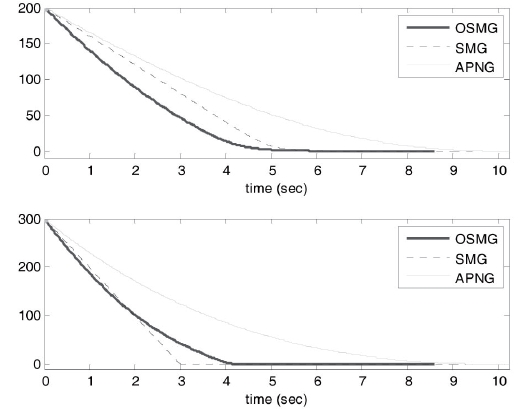
6.2 Tracking Errors, Final Time and Miss Distance
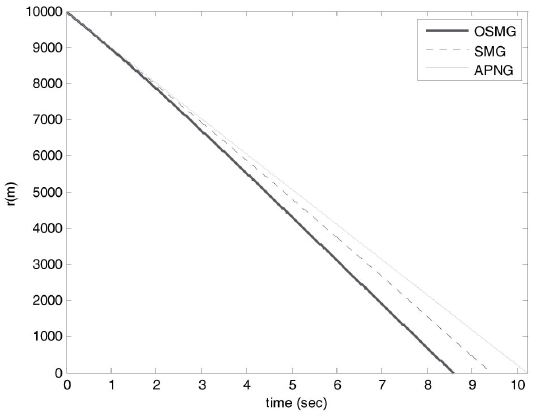
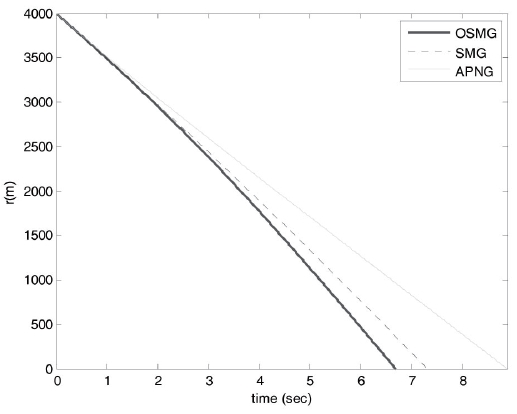
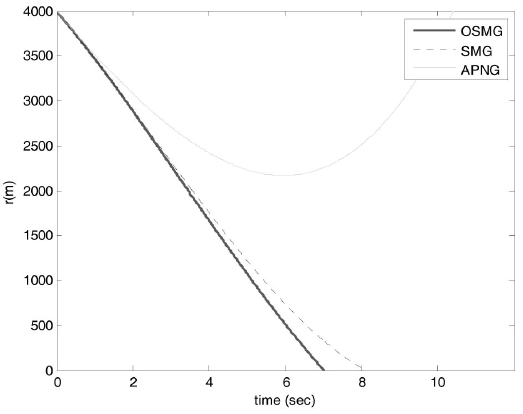
Our design purpose is to develop an effective guidance law to keep the pitch LOS angular rate, yaw LOS angular rate and relative distance as small as possible under uncertain target accelerations. From Figs. 4-7, it is obvious that the tangential relative velocities and relative distance for the optimal sliding-mode guidance design law all converge to zero faster than those of the other two laws for both cases.
The final time for the three guidance laws are 8.59s, 9.43s and 10.23s, respectively, in case 1 and 6.69s, 7.31s and 8.8s, respectively, in case 2. This finding reveals that the optimal proposed method possesses excellent target tracking ability, and it is possible to acquire smaller miss distances than those for the SMG and APNG. The miss distances in three guidance laws are 1.13m, 1.96m and 1.39m, respectively, in case 1 and 0.48m, 1.40m and 0.64m, respectively, in case 2.
As a result, OSMG not only causes a smaller final time and good tracking for the initial conditions in cases 1 and 2 (Figs. 4-7), it also generates smaller control efforts than those for SMG and APNG (Figs. 2 and 3).
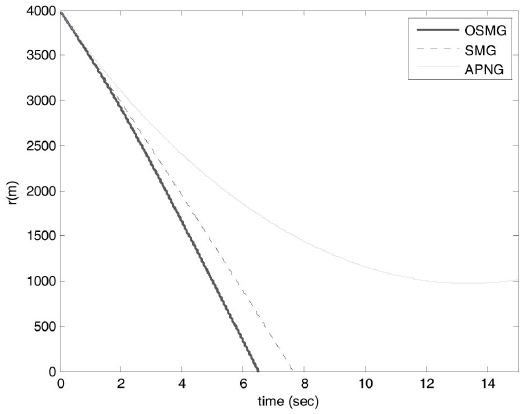
Robustness for the presented guidance law is investigated by three types of target maneuvers. In accordance with the definition of the performance robustness index, a robust guidance law should keep the engagement performance with less sensitivity to the external disturbances, i.e. the target acceleration commands. Although the successful
engagement in the APNG law is based on the assumption that information about the target acceleration profiles is exactly known, nevertheless for some target maneuvers it will become unstable. Simulation results in Fig. 8 and 9 have indicated it is difficult for the APNG to track the step and ramp target with the initial conditions of Case 2, but the proposed OSMG and SMG laws can still accomplish the missions. Consequently, the proposed guidance law is more robust to uncertain target accelerations than the traditional one in different initial conditions.
A new missile guidance law has been successfully developed against a highly maneuvering target by combining optimal and sliding-mode theories based on the state dependent Riccati equation to accomplish robustness against disturbances. The guidance command has been derived for 3-dimensional state space equations. The effectiveness of the presented sliding-mode part is proven by
the second method of Lyapunov. Robustness of the guidance law against disturbances was demonstrated by simulation results considering three different types of target maneuvers. By considering the different initial conditions for missile and target engagement, it has been shown that the final time and control fuel for the optimal sliding-mode guidance law is smaller than those for sliding-mode guidance and APNG laws. Furthermore, the presented guidance law is simple to implement in practical applications when compared to APNG.