Molecular weight distribution of polymers is closely related not only to the precursor’s tensile strength, impact strength, and folding strength but also to the liquidity, film forming ability, and spin ability in processing [1]. Therefore, it is important to control the molecular weight distribution of a poly(acrylonitrile) (PAN) precursor in order to enhance the properties of the carbon fiber. Especially, synthesis of a high molecular weight PAN is important to produce a high performance PAN precursor [2,3].

Because precipitation polymerization in solution maintains many advantages such as easy mixing and heat dissipation, easy controlling of the operation conditions, and easy overcoming of the shortcomings of the viscosity polymer system, it has become a very important polymerization method [4]. During the polymerization of AN into solution deionized water/ dimethyl sulfoxide (H₂O/DMSO), nano-sized solid particles were produced and coagulated, resulting in precipitation polymerization.

Wang et al. [5] studied how the weight ratio of solution(H₂O/DMSO) affected the viscosity- average molecular weight, conversion rate in polymerization, and morphological structure of the polymer. By studying the submicroscopic process of PAN’s negative ion precipitation polymerization, Zhang et al. [6] suggested a polymerization dynamic model and an equation, and proved that equations correctness via experiments. Li and Shan [7] studied how the weight ratio of solution (H₂O/DMSO) affected the thermal behaviors of the PAN polymer, and reported that the solution composition has a great influence on the molecular weight distribution and the structure of the products. However, there has been to date no report on any theoretical study of the molecular weight distribution (MWD) of liquid phase polymerization and solid phase polymerization in the precipitation polymerization of AN.

Therefore, the purpose of this study is the investigation of the MWD of polymers in liquid phase and the MWD of polymers in solid phase during the precipitation polymerization of AN. To attain our purposes, 1) theoretical reaction kinetics in liquid phase and solid phase were suggested to obtain the MWD, 2) the relationship between polymerization degree and solution concentration (H₂O/DMSO) was determined at different temperatures, and 3) interpretation of the reaction kinetics was carried out by changing the concentration of H₂O/DMSO in order to control the MWD of the precipitated PAN precursor.

In the process of AN precipitation polymerization, there are two factors: the liquid phase polymerization and the solid phase polymerization can be suggested as being important in the formation of the MWD of PAN.

Factor I is regarded as the liquid phase polymerization. In the precipitation polymerization of AN, the propagation radical (M？) can move in the DMSO solvent, resulting in a reaction that easily terminates and an average polymerization degree

that is very small. Nascent polymer chains can be obtained.

Factor II is regarded as the solid phase polymerization. In the precipitation polymerization of AN, the obtained polymer is not dissolved in the H₂O/DMSO mixture solution. Once it is generated, it becomes nascent particles and is suspended in the solution. At the core, the nascent particles aggregate with other particles until they become a larger particle in the precipitation polymerization. In this process, some propagation radicals will be everywhere among the nascent precipitation particles. These propagation radicals cannot easily be moved, and the chance to terminate the adjacent two propagation radicals drops. In this case, propagation radicals will have many more chances to continue to react and, finally, to form larger molecules.

According to statistics theory, we define the distribution function as N_xL = f_L ( x ) in liquid phase polymerization; in solid phase polymerization, the distribution function is defined as N_xS = f_s ( x ). If the consumption volumes of AN in the liquid phase and the solid phase are V_L and V_S, respectively, and f_L ( x ), f_S ( x ) are the molecular numbers for the liquid phase and the solid phase polymerization, respectively, N_x = V_L f_L ( x ) V_S f_S ( x ) can be obtained. Then, V_L/V_S = r is the contribution ratio of the liquid phase and solid phase polymerizations. r can be controlled in experiments.

Due to the free radical polymerization mechanism, elementary reactions in liquid phase polymerization can be obtained as follows:

where I is an initiator, M is a monomer, R？ is the free radical, M？ is the radical segment, and P_x and P_y are thepolymers.

Based on the above elementary reactions, the reaction kinetics equation of liquid phase polymerization can be established. Due to the existing double-base terminate reaction in the liquid phase polymerization, the steady-state condition can be used, and so:

where

is the liquid phase chain transfer constant, and [M_t？] is the total concentration of free radicals.

Deducing the recurrence formula:

Because of

ktL is larger than k_pL by 3~5 orders of magnitude, and [M] is larger than [M_t？] by 10 orders of magnitude. So:

where 2 fk_dL [ I ] + k_trL [M_t？][M] refers to the conduction speed of [M₁？]. Each [M₁？] will necessarily generate a polymer chain, and so the whole concentration [P_t] of polymer chains can be expressed as the following equation.

Therefore:

Elementary reactions in solid phase polymerization are as follows:

Considering that double-base termination between two active chains cannot occur easily in solid phase polymerization, the elementary reaction can be approximately ignored. So, the effective elementary reactions are:

Based on the above elementary reactions, the reaction kinetics equation of solid phase polymerization can be established, as follows:

The above reaction kinetics equations indicate that the steady-state hypothesis cannot be used here. Therefore, a series of nonhomogeneous linear equation need to be solved.

In order to deduce conveniently, variable substitutions are needed: dτ = [ M ]dt and τ = [ M ]t, substituting the subscript S for k.

On the other hand, considering that the monomer and initiator can come in and go out in the precipitation phase gap, approximate conditions, such that [ I ]/[ M ] still maintains similar values within a wide range of conversion rate, can be used. Therefore:

where A is constant. So:

Special solutions can be obtained as follows:

Given:

Therefore:

Thus continuous solutions can be obtained as follows:

So:

where, according to the parameters in Pan’s [8] book, monomer concentration and polymerization time of the polymerization system,

can be known, and so the simplified formula is available:

From the above, the total distribution function of the molecular weight can be obtained:

where

Due to the number distribution function, the integral distribution function of weight can be expressed as the following equation.

where Q is the MWD, which can be found through gel permeation chromatography (GPC). C_mL and C_mS can be obtained separately from Eqs. (26) and (27). When the solid phase polymerization accounts for 100%, r=0, the limit MWD of PAN can be obtained from Eq. (25) as Q=2.

The reaction kinetics theory of the macromolecule can be used to easily infer that: polymerization degree of AN in 100% water can be expressed as follows:

On the other hand, the following equation can be obtained from the solution polymerization of AN in DMSO.

If

S (H₂O/DMSO→∞) and

L(H₂O/DMSO→0) are known, the above two kinds of polymerization equations can be used separately to determine C_mS and C_mL. Different temperatures lead to different values. The value of r can be obtained when Q is known. Generally,

L and

are both calculated using the equation

where the weightaverage molecular weight is obtained under limited conditions.

AN (Beijing Chemical Reagents Co.) was used for polymerization. AN was freed from inhibitors by distillation at 76~78℃ before polymerization. DMSO and H₂O were used as polymerization solvents. α,α’ -azobisisobutyronitrile (AIBN) was used as an initiator. AIBN was purified by recrystallization. Dimethyl formamide (DMF) solution was used to measure the intrinsic viscosity of the polymer.

Polymerization progressed following the steps detailed in previous reports [9,10]. Basically, 0.1 L AN and 0.3 L solvent were mixed in a three-necked glass reactor. The solvent component was controlled by changing the volume ratio of H₂O (from 0.1 to 1.0 wt% to the amount of DMSO) and DMSO. One wt% AIBN was added as an initiator; it did not affect the volume ratio of the solvent. Polymerization was carried out by changing the reaction temperature from 50℃ to 65℃ for 2 h, at 30 rpm, and under a pure nitrogen atmosphere. During the polymerization, newly produced PAN nano particles were found to precipitate. After the polymerization finished, the precipitated PAN slurry was filtered and washed with acetone several times; it was then vacuum dried at 50℃ for one day until it was possible to obtain completely dry samples. Then, the intrinsic viscosity and MWD were investigated.

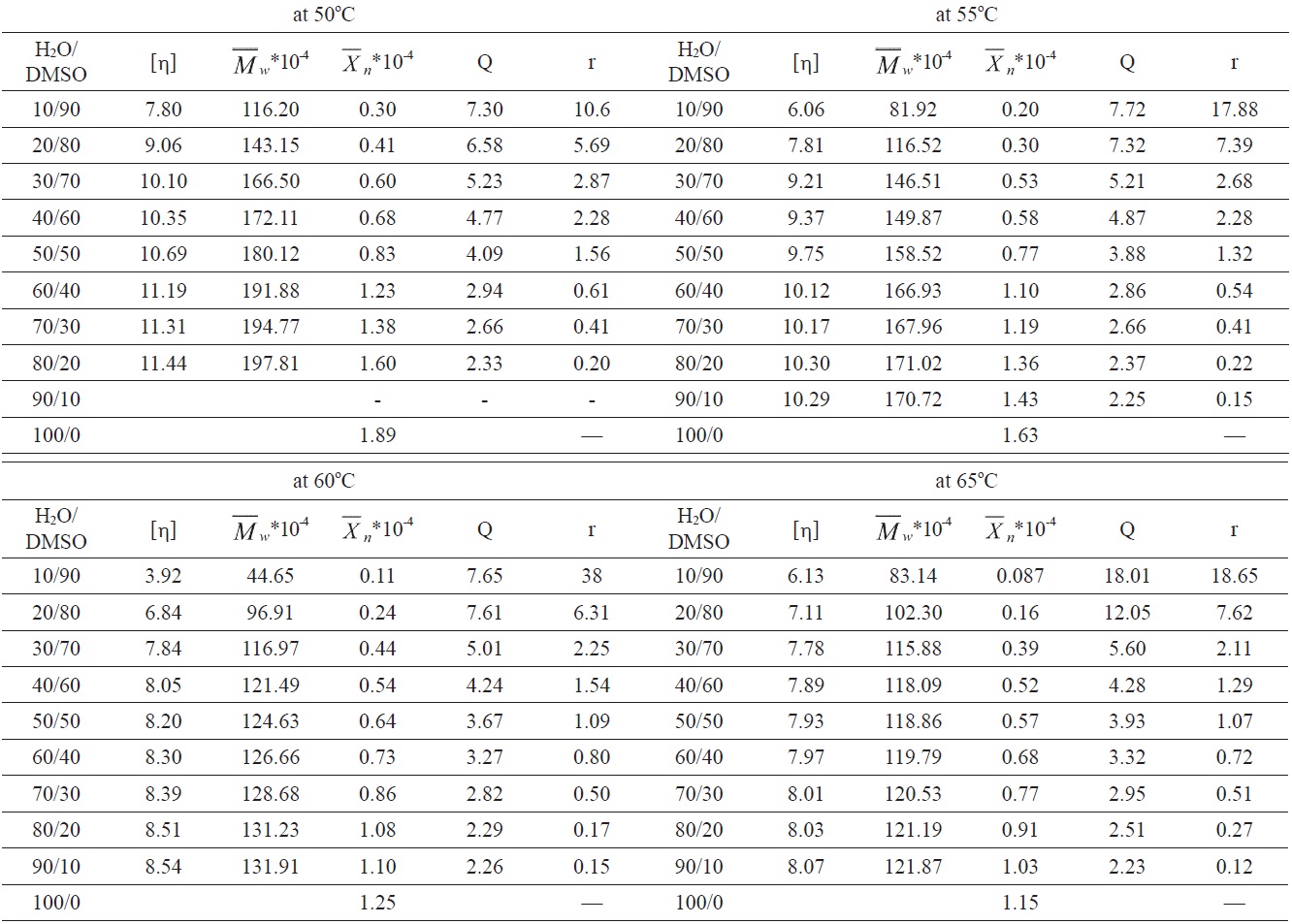
The intrinsic viscosity [η] of the obtained polymers was measured in DMF solution using an Ubbelohde viscometer in a water bath at a constant temperature of 25 ± 0.5℃, following Kashyap’s method [11]. The weight-average molecular weight

was calculated from the following equation [12]:

Then, GPC (self-made) was used, with DMF as the solvent, at a temperature of 25℃, to test and to obtain the MWD (Q).

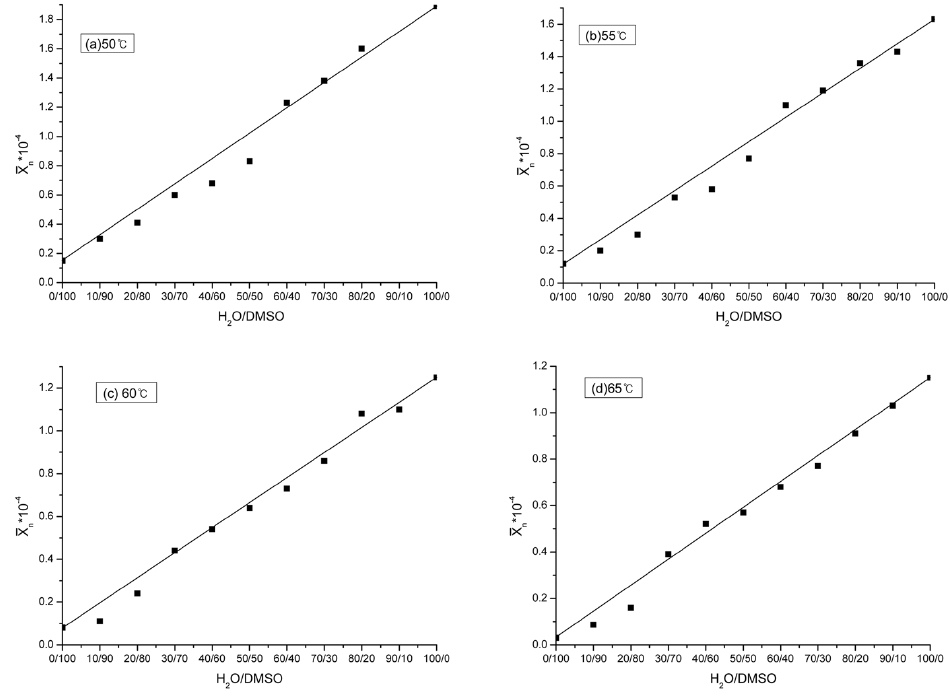
Fig. 1 shows relationships between the average polymerization degree of the PAN homopolymer and the H₂O/DMSO ratio at different reaction temperatures.

Ls could be obtained from the intercepts when H₂O/DMSO→0; these intercepts were 0.15 at 50℃, 0.12 at 55℃, 0.08 at 60℃, and 0.03 at 65℃; it was possible to obtain the value of C_mL s from Eq. (27). All the results showed that the average polymerization degree of the PAN homopolymer linearly increased with the increase of the H₂O/DMSO ratio due to the increase of solid phase polymerization. However, they decreased with the increase of solution temperature, because the termination rate of the chain increased with the increase of the solution temperature. Some researchers have reported similar results for the effects of H₂O/DMSO ratio and solution temperature [13,14]. The obtained molecular weights are listed in Table 1, as a function of H₂O/DMSO ratio. Q was measured, and r was calculated using Eq. (25). Q and r are also listed together.

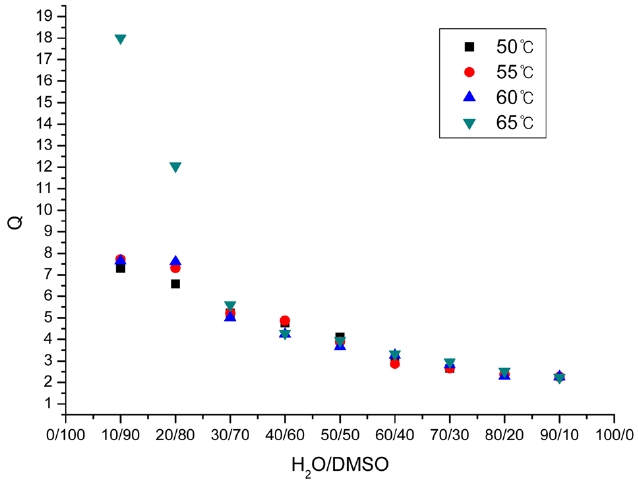
Fig. 2 shows the relationships between Q, r, and the H₂O/ DMSO ratio at different reaction temperatures. With the increase

of water content, r decreased and approached 0. The MWD also decreased and approached 2. This was because the solid phase polymerization increased with the increase of the H₂O/DMSO ratio, and the solid phase polymerization was believed to be similar to the bulk free radical polymerization, resulting in the MWD moving close to 2. These results coincided well with the theoretical equation derived from the mechanisms.

According to the kinetic mechanism, which says that the liquid phase polymerization and solid phase polymerization are different in the polymerization of acrylonitrile, the relation between the contribution ratio r and the MWD (Q), shown in Eq. (25), can be derived. In the precipitation polymerization, the contribution ratio r decreased and approached 0; the MWD also decreased and approached 2 with the increase of the H₂O/DMSO ratio due to the increased solid phase polymerization. The experimental data were found to coincide well with the theoretical equation derived from the mechanisms. The results have a certain guiding significance for the setting of process parameters in the precipitation polymerization of acrylonitrile and in the adjustment of the MWD of PAN.