Like archeology, which uncovers the history of the human species by studying its remnant artifacts, astronomers uncover the history of the Galaxy by studying the remnants of past generations of stars. White dwarfs are by far the most common end product of stellar evolution. At least 95 percent of all stars end this way (Koester 2002), essentially as inert carbon/oxygen cores of what used to be red giant stars, enveloped by thin atmospheres of hydrogen and helium that moderate the loss of thermal energy into space. The fact that this cooling process takes billions of years makes white dwarfs valuable tools for “cosmochronology” (see the excellent review of this topic by Fontaine et al. 2001).

White dwarfs have played important roles in rather diverse areas of astrophysics. Some of these include relativity theory, stellar evolution theory, Galactic structure and even cosmology.

The companion to the brightest star in the sky, Sirius B, provided one of the first empirical confirmations of Einstein’s theory of general relativity (an excellent historical account is given by Holberg 2007). After the masses of the two stars had been determined from the astrometric orbit, the Balmer lines in the spectrum of Sirius B were found to be red-shifted by an amount unrelated to its motion in space. This gravitational redshift, typically a few tens of km/sec, confirmed the extremely high densities of white dwarf stars and is now commonly used to measure their masses. In conjunction with parallaxes and luminosity measurements, white dwarf gravitational red-shifts provide a rigorous test of the theoretical mass-radius relation for electron-degenerate gas (Holberg et al. 2012).

The observed properties of white dwarfs are essential “boundary conditions” for stellar evolution theory. Any evolutionary model for main sequence stars below 8-10 M_⊙ that does not yield a remnant of mass, radius and composition in agreement with the rather limited ranges of these variables seen among white dwarfs in the solar neighborhood is simply unphysical. The distributions of white dwarfs in space and by mass are encoded records of the star formation (and death) rate throughout the history of the Galaxy, as well as the fraction of mass recycled into future generations of stars. These are important constraints on the metal enrichment history of the Galaxy. In addition, their cooling ages, radial velocities, space motions and atmospheric compositions are probes of the dynamics and abundance evolution of the thin and thick disk in the solar neighborhood.

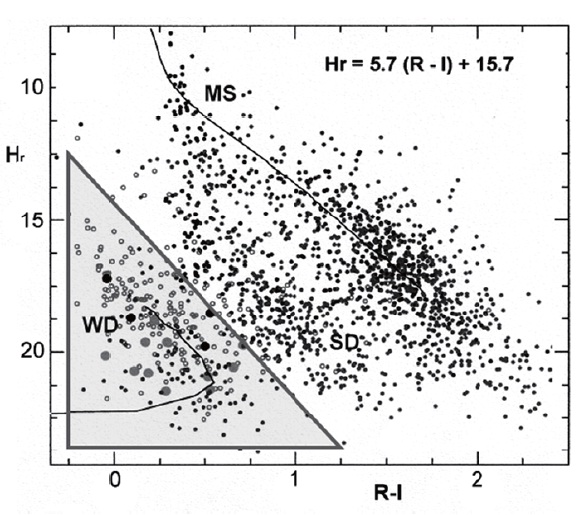
Most white dwarfs have been found by searching for faint nearby objects of high proper motion and appropriate

color. Luyten (1944) was perhaps the first to use a so-called “reduced proper motion diagram” to identify white dwarf candidates. In such a diagram, the ordinate is reduced proper motion H = m + 5 log μ +5, where m is an apparent magnitude in some specific band pass and μ is proper motion in arcsec yr^-1. The abscissa is any arbitrary color index. Lacking the latter, Luyten used crude “color classes” defined by direct visual comparison of each star’s image on two plates taken through different filters. Fig. 1 shows a reduced proper motion plot using the R-I color index: nearby faint, white, rapidly moving objects fall into the lower left corner (shaded triangle). Using this technique, Luyten (1941, 1949, 1964, 1974, 1979) found several thousand white dwarf candidates, many of which were later spectroscopically confirmed by observers such as Eggen & Greenstein (1965 et seq.) and Oswalt et al. (1988).

Because of their very high proper motion, white dwarfs in the Galaxy’s halo would be found at the bottom of Fig. 1. However, due to their low space density, they comprise at most a few percent of stars in the solar neighborhood (Chiba & Beers 2000). This extremely old population is expected to be rich in white dwarfs. In a study of new very faint white dwarfs identified in a new deep proper motion survey, Oppenheimer et al. (2001) found about 50 of very high proper motion, suggesting they were halo members. The space density implied by their sample appeared to be more than adequate to explain the entire dark matter content of the Galaxy. Eventually, the sample was shown to most likely be part of the extended tail of the thick disk population (Reid et al. 2001, Silvestri et al. 2002) and the revised space densities suggested that white dwarfs do not constitute more than a few percent of the dark matter content of the Galaxy.

Lacking thermonuclear sources of energy, white dwarfs slowly cool at a rate moderated by the composition of their thin hydrogen- or helium-rich atmospheres. In the same manner that a crime scene investigator uses a victim’s body temperature to set an approximate time of death, the cooler a white dwarf, the older it is. Because the cooling rate of a white dwarf slows down, cool white dwarfs are expected to be far more numerous than hot young white dwarfs. This effect is manifested by the white dwarf luminosity function, a plot of the space density of white dwarfs as a function of luminosity. A turn-down in the white dwarf luminosity function at the faint end was interpreted to be a direct consequence of the finite age of the Galaxy (Winget et al. 1987, Liebert et al. 1988).

White dwarf stars have directly contributed to the resolution of several important cosmological problems. In the 1990’s early results from the Hubble space telescope (HST) on the expansion of the Universe suggested a cosmic age of less than 10 Gyr. At the same time, new model fits for globular cluster color-magnitude diagrams derived from deep HST observations indicated ages up to 16 Gyr. Clearly these results were incompatible (see Lineweaver (1999) for an excellent summary). During the same period of time several groups were working on constructing a definitive white dwarf luminosity function (Oswalt et al. 1996, Leggett et al. 1998, Knox et al. 1999). All of these studies suggested a minimum age for the Galaxy’s disk component of at least 10 Gyr, implicating a problem with the Hubble age determination. Since then, incorporation of the effects of inflation and acceleration have increased the Hubble age to about 13.7 Gyr and improved models have brought the ages of the oldest globular clusters into line with that limit. However, the age derived from the white dwarf luminosity function has remained virtually unchanged, except for modest improvements in precision.

Because the amount of mass that can be accreted onto a white dwarf from close evolving companion is strictly limited by the Chandrasekhar relation, the luminosity of a supernova of type SN-Ia is also strictly constrained. Thus, such systems provide one of the most important “standard candles” for cosmological distance determinations and directly contributed to the discovery of the acceleration of the Universe and dark energy (Riess et al. 1998, Perlmutter et al. 1999).

White dwarfs may even be regarded as “exotic particle detectors.” The shape of the bright end of the white dwarf luminosity function is only sensitive to the averaged cooling rate of white dwarfs. Isern et al. (2008) proposed using this property to check for the possible existence of axions, one of the proposed constituents of the “missing mass” component of the Galaxy. Their models suggested that the axion mass is of the order of a few MeV and that the white dwarf luminosity function is sensitive enough to detect their existence.

In the course of their proper motion surveys Luyten (1964, 1974, 1979) and Giclas et al. (1971, 1978) drew special attention to over 500 fragile binaries with suspected white dwarf components. Low-resolution spectroscopic identifications by Oswalt et al. (1988, 1991, 1993) currently account for ~10% of the entries in the most recent Villanova Catalog of Spectroscopically Identified White Dwarfs (McCook & Sion 1999; entries marked with “b” for binary). Newer searches by Pokorny et al. (2003), Chaname & Gould (2004), Lepine & Shara (2005), and Smith et al. (2005) identified many new potential fragile binaries in the solar neighborhood. Chaname (2007) searched the SDSS for nearby fragile pairs in the halo. Zhao et al. (2012a) showed that the SDSS contains ultra wide pairs at distances well beyond the solar neighborhood (>1 kpc). Clearly there are many fragile binaries left to be found!

A sizable fraction of the white dwarfs closest to the Sun are in fragile binaries (Holberg et al. 2008). The observed properties of such nearby evolved pairs are minimally affected by interstellar reddening, space density variations, scale height, abundance gradients, etc. Also, the main sequence companions’ spectra provide benchmarks for ages, space motions, gravitational redshift masses, etc. which are often difficult or impossible to determine for single white dwarfs (Reid 1996, Silvestri et al. 2001, 2002, 2005).

White dwarfs in fragile binaries are most often accompanied by cool main sequence companions of spectral type F, G, K or M with mean separations of about 10³ a.u. (Greenstein 1986a, b). Each component of a given pair has evolved independently, unaffected by mass exchange or tidal coupling that complicate the evolution of closer pairs. Moreover, components of a fragile binary are coeval. Essentially, they may be regarded as an “open clusters with only two components,” but they are far more numerous than clusters and span a much broader and more continuous range in age and metallicity.

Age is arguably the most difficult to measure property of a star. Zhao et al. (2012a) showed that fragile binaries with two main sequence components have consistent chromospheric activity, which is a well known proxy for age (Mamajek & Hillenbrand 2008). Rotation rate is also well-known to correlate with age (Barnes 2007). However, the activity- and rotation-age relations currently rest on a handful of nearby clusters that span a very limited range of ages. Using pairs consisting of a lower main sequence star with a white dwarf companion from which a cooling age could be determined, Zhao et al. (2011) examined the activity-age relation. Chaname & Ramirez (2012) have begun to examine the rotation-age relation using fragile binaries containing a main sequence star with an evolved component (subgiant or giant) from which isochrone ages can be determined.

Post-MS mass loss leads to orbital expansion in fragile binaries (Fig. 2, adapted from Johnston et al. 2012). Their present separations reflect the amount of mass lost by the binary during post-main-sequence evolution. In modeling the observed distribution of apparent separations among evolved fragile binaries, Johnston et al. (2012) demonstrated the expected increase in orbital separation, as well as perturbations to the associated orbital parameters.

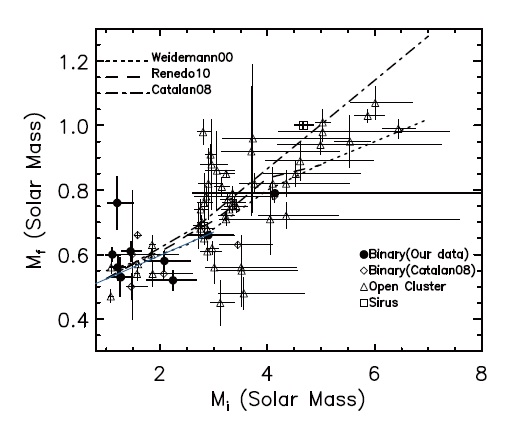
In general, the higher the mass of a white dwarf’s progenitor, the higher the mass of its remnant. This “initial-final mass relation” (IFMR) is a key constraint on stellar evolution theory. It characterizes the amount of material the vast majority of stars recycle to the interstellar medium. Accordingly, it is also essential to understanding the chemical enrichment and the star formation history of the

Galaxy, and by inference other galaxies.

Unfortunately, the observational verification of the IFMR has proven to be difficult; the observational data shows far more scatter than predicted by theory (Fig. 3). Most work on the IFMR has focused on nearby open clusters bright enough for the white dwarf cooling track to be observed and those tend to be much younger than the Sun. Because of this, the initial masses of the majority of white dwarfs in the empirical IFMR tend to be rather high. Recently, Zhao et al. (2012b) investigated the low-mass end of the IFMR using fragile binaries, which tend to be much older than nearby clusters. For the white dwarfs plotted in Fig. 3 as filled circles, the spectra of their main sequence companions were used to estimate the total age and original metallicity of each pair. Balmer line fits were used to obtain the cooling age of each white dwarf component. The difference provided an estimate for the main sequence lifetime of each white dwarf progenitor, from which its original mass was determined by interpolating among metallicity-dependent evolutionary models for the progenitor (Girardi et al. 2000).

The error bars shown in Fig. 3 cannot account for the entire scatter seen in the observed IFMR. A clue to the cause of this scatter may be seen in this figure. WD2253-08 (M_i = 1.20 M_⊙, M_f = 0.76 M_⊙) is an outlier. It has a main sequence companion with unusually low metallicity, [Fe/H] = -0.40. This prompted Zhao et al. (2012b) to investigate whether metallicity can account for some of the scatter seen in the IFMR.

Fig. 4 shows the fractional mass lost during post-MS evolution vs. metallicity for the white dwarfs in fragile binaries for which their original metallicity [Fe/H] could be obtained from their main sequence companions’ spectra. The five DA white dwarfs with hydrogen-rich atmosphere all have initial masses Mi < 2 M_⊙ for which metallicity-dependent post-main-sequence evolutionary models are available. Apparently, high metallicity progenitors lose up to twice as much mass as low metallicity stars as they become white dwarfs. Work is underway on models to determine whether the relation can be extended to the higher masses and/or helium-rich white dwarfs shown in this figure.

After having been virtually ignored for decades since the Luyten and Giclas proper motion surveys identified them, fragile binaries are at last being recognized for their potential to provide fresh approaches to difficult astrophysical problems. The oldest pairs, which often contain white dwarfs, provide a window on the deep history of the Galaxy. During the next decade, as huge surveys such as the panoramic survey telescope & rapid response system and the large synoptic survey telescope come on line, fragile binaries will be identified by the millions and the leverage they provide on the problems outlined above, as well as many others, will be fully realized.