The contemporary era is characterized by a high degree of involvement of computers harvesting data in various aspects of everyday life. From simply carrying a cell phone to traveling and from casual shopping to receiving medical aid, all these activities induce the collection of large volumes of information that also include private data. These independently stored data often need to be integrated.

Combining independently stored information could benefit a large number of domains, such as medical research and public safety. For instance, information integration could lead to the creation of a public safety early warning system. Consider, as an example, the recent H1N1 flu outbreak. Each time a person was found to be infected with the disease, attempts were made to spot his/her recent activities to prevent the spread of the epidemic by locating possible candidate patients. A typical example is the case of airline travelers. When a passenger is found to be infected with the H1N1 virus, a significant effort is made to locate people who traveled on the same flight.

An effort like this would be much more successful if an early warning monitoring system existed that would locate and inform possible patients by integrating data from an airline’s passenger list in our case, with the patient list in hospitals. When a traveler is found to be infected with the flu, the other passengers can be instantly alerted. Such a system however would require the preservation of privacy of both patients and travelers. In the case in which the hospital integrated travel and medical data, no information should be revealed to the hospital database administrator regarding names of passengers. Correspondingly, if the airline managed to merge this information, the medical record of the patients should not be fully exposed.

Technically speaking, what we have presented previously is a modified version of the classical record matching problem. In classical record linkage, separate dataholders maintain data corresponding to the same real world entities (people, cases, events,etc.) without necessarily maintaining common and unique linkage identifiers. Dealing with non-unique identification information is an important deficiency that needs to be addressed by all the record linkage algorithms. Additionally, in database fields, such as names, and addresses, typing or spelling errors that may accidentally occur make this task even more difficult. It is obvious that this is a task of increased complexity. As such, a technique called blocking has been introduced to improve performance[1]. Private record linkage features an additional major complication during data matching: all data stored within independent repositories contain sensitive individual information.

Therefore, any attempt towards data integration would lead to privacy breaches, ra_ising ethical and legal issues: certain legislation,such as the EU Data Privacy Directive [2], render each company responsible for maintaining the privacy of its stored data and any explicit leaking might lead the dataholder to face prosecution. It is evident that performing data linkage, while preserving privacy is an important problem that needs to be taken seriously into consideration.

To be more concise, the core of the private record linkage problem renders the ability of merging data from two or more databases in a way that the only additional information that each of the database owners gain, will only refer to entities already stored in his own database before integration.

In this paper, we propose a complete framework for addressing the problem of privacy preservation approximate record matching. We achieve this by enhancing Edit Distance based methods used for conventional approximate record matching with privacy-preservation characteristics and increasing matching performance by facilitating a secure blocking component based on phonetic codes. We prove our assertions that our approach offers the same accuracy with traditional edit distance algorithms, while it respects privacy and compare our results to a rival algorithm by extensive experimentation.

In the privacy preservation record linkage protocol we propose,we assume that all parties exhibit an Honest But Curious behavior (HBC). All parties are honest in the sense that they are all obliged to follow the protocol. They are curious, since they maintain every new knowledge acquired during the execution of the protocol. Our protocol satisfies these restrictions, since no new information is revealed, apart from integrating complementary information regarding known real world entities.

The contribution of this paper is multidimensional. First, we propose a complete framework towards secure approximate matching. Second, this framework consists of a secure blocking component and a secure matching component featuring an open architecture. Openness is a very important feature, since we do not provide a single monolithic technique, but a framework which allows the usage of a variety of techniques depending on their suitability in each case. Third, we propose a secure blocking component enhanced by three levels of privacy: phonetic encoding, encryption and random noise insertion in the form of fake phonetic codes. Fourth, we propose an approximate private matching algorithm by enhancing with security the widely used Levenshtein distance algorithm [3], while maintaining intact its matching accuracy. Fifth, we present an in-depth security analysis of our approach. Finally, we provide a set of extensive experiments that prove the correctness, security and high performance of our approach.

The remainder of this paper is organized as follows. Section II presents previous work related to ours. Section III provides necessary background knowledge. Section IV presents the proposed private matching framework. Section V contains the evaluation of our methodology in terms of complexity and privacy.Our approach is empirically assessed in Section VI. Finally,Section VII contains conclusions and future research directions.

Record matching (or linkage) is a rather old yet important area of research. As such, numerous methods have been proposed to address the problem. A detailed analysis of all major currently used methods can be found in [4]. Approximate string matching methods consider comparing strings to possible typographical errors. These methods fall into three major categories:token-based methods, distance-based methods and phoneticsbased methods.

Token-based methods calculate tokens of the strings to be matched and then count the number of common tokens. Ngrams based methods fall into this category [5]. Distance-based methods measure the differences between strings. Some of the most widely used methods are Levenshtein distance [3], the Jaro [6] and Jaro-Winkler metrics [7, 8]. Conversely, phoneticsbased methods make use of certain string transformations to take advantage of the way words sound for purging the effects of various typing and spelling errors. Typical examples of this class include Soundex [9], Metaphone [10], ONCA [11], and NYSIIS [12]. Based on all the aforementioned methods, a variety of systems, such as Tailor [13], Febrl [14] and WHIRL [15]has been developed to perform approximate record linkage.

Research directions were provided in [16] stating the needs and problems of this research field regarding privacy-preserving matching. State of the art in token-based privacy-preserving matching includes the work of Churches and Christen [17] who propose deidentifying the dice coefficient of n-grams using hashing. However, approaches relying on [17] suffer from very high complexity. Privacy preservation of distance-based methods,such as Edit Distance [18] and the Jaro-Winkler string metric[7] performed well only in cases of non-encrypted data, as indicated in [19]. Previous work in privacy-preserving phonetics-based matching required the existence of a trusted third party [20]. Moreover, as detailed in Trepetin’s survey [21],some attempts to address the problem of privacy-preserving record linkage fall short in providing a sound solution, either because they are very resource intensive [22, 23] or because they are unable to provide both matching accuracy and fault tolerance[24].

Approaches that are more recent include the one suggested by Inan et al. [25] that uses a hybrid scheme combining cryptographic methods with anonymization techniques creating value generalization hierarchies. Scanapiecco et al. [26] achieve privacy-preserving data matching using embedding spaces and schema matching based on a global schema. The privacy properties of k-anonymity on joins explored by Kantarcioglu et al.can by found in [27]. Guidelines to build a privacy-preserving matching system are detailed in [28] and a categorization of recent approaches in [29]. The latest work in this field is by Inan et al. [30] based on differential privacy.

Atallah et al. [31] proposed an approach that resembles our methodology, where the edit distance algorithm is modified to provide privacy to genome sequence comparisons. This approach was aimed towards sequence comparisons and has considerable communication cost. In contrast, our methodology has low communication cost, since it targets data stored in files or databases.

Bloom Filters [32] are an essential part of our architecture.They have been used in a variety of contexts, ranging from indexes for XPath queries [33] to summary caches [34]. Schnell et al. [35] proposed a method based on a combination of bigrams and Bloom filters regarding private record linkage. Each matching party creates a Bloom Filter where bigrams are stored.Then, one party manages to compare the filters by performing a logical AND on them and calculating similarity in terms of common bits, using the Jaccard coefficient.

In this section, we provide the necessary background required to present our methodology, along with a running example used throughout the rest of our paper. Specifically, we describe the phonetic algorithms and distance-based matching methods.Moreover, we present the operation of Bloom filters and their extension, counting Bloom filters used in our approach, and discuss guidelines for selecting the appropriate hash functions for our framework.

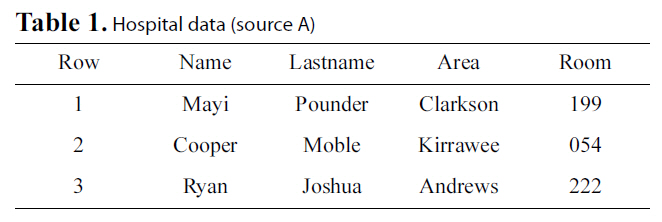
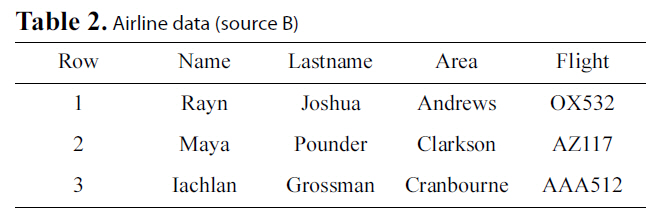
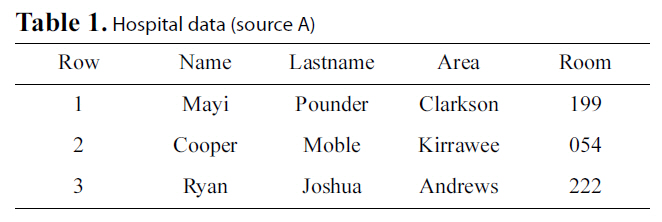
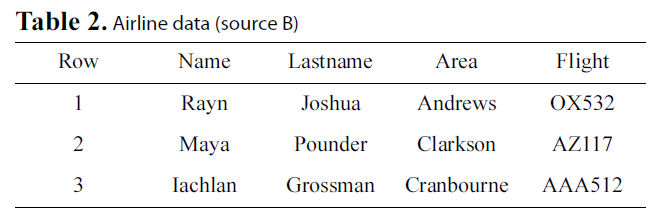
Let us go back to the example presented in the introduction,where we wish to integrate a hospital’s database with the database of an airline to locate possible H1N1 patients. We consider two parties, A that will represent the hospital database (Table 1)and B that will represent the airline database (Table 2). These two parties will also be referred to as sources.

Both databases hold sensitive information that can be used to uniquely identify individuals. For simplicity, we will assume that both databases have different schemas but share a common subset of attributes, i.e., Name, Lastname, and Area. These data will be referred to as private data, because they should not be revealed. These fields will be used for record linkage as well.Additionally, each of the two databases holds quasi-identifiers.These are data that are not self-descriptive of real world entities,but provide private information if combined with the private

[Table 1.] Hospital data (source A)

Hospital data (source A)

[Table 2.] Airline data (source B)

Airline data (source B)

data. Let us assume for the hospital that this is the Room field and for the airline the Flight field.

Our aim is to integrate these two databases in such a way that neither the hospital will be aware of all of the airline’s passengers,nor the airline will get any knowledge regarding the hospital’s patients. The only knowledge that will be gained by both parties will be over the airline passengers that have been hospitalized for the influenza virus. In the next section, we will illustrate the operation of approximate matching algorithms used in their original forms. Data from this example will be used to do this.

A phonetic algorithm is an algorithm to match words based on their pronunciation. Phonetic algorithms have been broadly used in the past for record matching performed on names. The main feature of the phonetic algorithms is their fault tolerance against typographical errors. For illustration purposes, we will use Soundex [9] in this paper. However, our methodology can be easily applied to other phonetic algorithms.

The operation of Soundex is quite straightforward: for each word to be encoded certain rules of grouping similar sounds are applied. The result is a four character hash that represents the pronunciation of the word. This hash consists of a capital letter followed by three digits. For example for the word “Cooper”, its Soundex code is C160.

Distance-based methods employ functions that map a pair of strings to a real number [36] Levenshtein distance [3] is the best known representative of distance functions. It measures the minimum number of operations required (insert, delete, replace)to transform one string to another. Here, two strings are said to match if their distance is less than d operations, d > 0. For example, consider the word “ryan” from Table 1, its distance from “rayn” of Table 2 will be 2, since two modifications (two replacements) are required to transform one word to another.

A Bloom Filter [32] is a method for representing a set A = α₁,α₂, . . . α_x of x elements (also called keys) to support membership queries. The idea is to allocate a vector v of y bits, initially all set to 0, and then choose z independent hash functions, h₁, h₂,. . . , h_z, each with range 1, . . . , y. For each element αi in A, the bits at positions h₁(a_i), h₂(a_i), . . . , h_z(a_i), in v are set to 1. (A particular bit might be set to 1 multiple times). Given a query for b,we check the bits at positions h₁(b), h₂(b), . . . , h_z(b). If any of them is 0, then certainly b is not in the set A. Otherwise, we conjecture that b is in the set although there is a certain probability that we are wrong. This is called a “false positive”.

A Bloom Filter extension is the Counting Filter proposed by Fan et al. [34]. In this construct, a counter is used consisting of three or more bits, instead of a single bit per position. Thus, the number of elements inserted in the filter may be explicitly computed.The operation of Bloom Filters is based on the hash function used to encode items to be inserted. This function should be both secure and provide a uniformly distributed hash. For this purpose, we selected the MD5 hashing algorithm [37] due to its broadly studied properties and as it is considered relatively fast.

In this section, we will put the pieces together and delve into our proposed protocol. We formally define the following notation to be more precise with our description. A and B are the two data sources used in our setup that will also be referred to as parties or dataholders. Each of them holds data within relations R_A(A₁, . . . , A_k) and R_B(B₁, . . . , B_l) respectively. We assume that even though the participating sites do not share a common schema, matching is still performed on a bare minimum of overlapping fields that exist in both sources A and B.

Thus, we will define two additional relation types. First, the Blocking Schemas that for A and B will respectively reflect relations R_A^BL( A₁^BL, . . . ,A_N^BL ) and R_B^BL(B₁^BL , . . . ,B_N^BL ). Each of these relations contains n fields with n ≤ min(k, l) that will be referred to as Blocking Fields or Blocking Keys. These fields are used in the Blocking Component of our framework.

Second, the Matching Schemas that for A and B are represented by R_A^M(A₁^M , . . . ,A_m^M ) and R₁^M(B₁^M , . . . ,B_m^M ), respectively.Each of these relations contains m fields with m ≤ min(k,l), which hence will be termed Matching Fields or Matching Keys. These fields are used in the Matching Component of our protocol. For either of the two parties, these datasets are related as follows: R^BL ⊆ R and R^M ⊆ R.

Considering the two data sources A and B, the privacy-preserving record linkage problem boils down to performing record matching between R_A and R_B with an additional constraint.At the end, source A will only know the subset of B’s data that match A’s data. Equivalently, B will only acquire the subset of A’s data that match its own data. Notice here that all the other parameters of the record linkage problem addressed remain as in the classical case. This means that our proposed methodology can equally well deal with non-unique identifiers,as well as data of low quality.

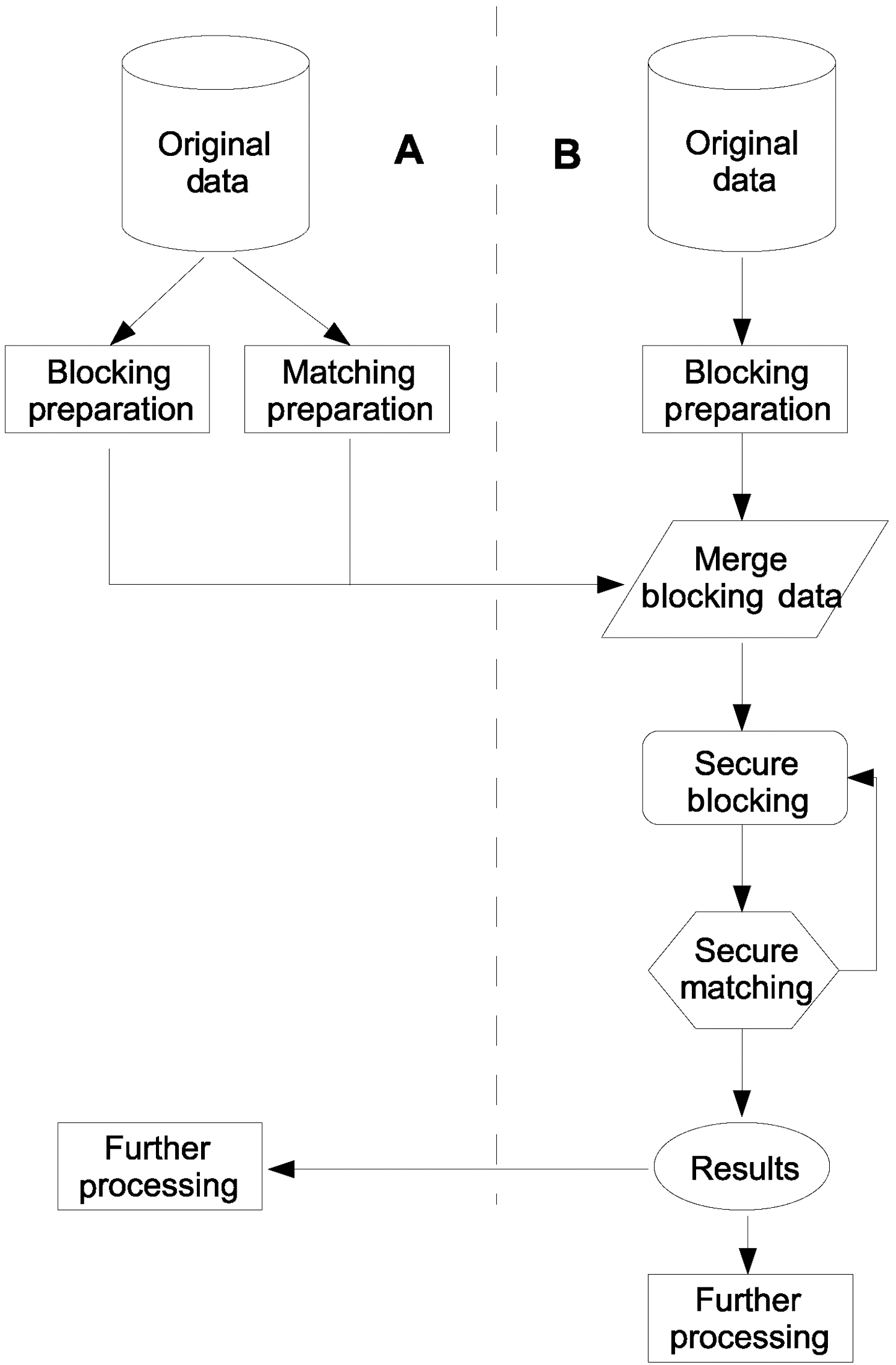
We will now provide a generic view of our protocol before we introduce the reader to the specific components of our solution,as illustrated in Fig. 1. First, the two matching parties A and B will prepare their data to be used in both Private Blocking and Private Matching components. Then A delivers its prepared data to B. B now merges his own blocking data with A’s. The secure blocking component is now initiated. After the completion of blocking, the private matching component begins its operation. The overall matching sequence of our framework consists of several blocking and matching passes. Therefore,after secure matching concludes, a new blocking pass begins.When the entire process is complete, B holds the matching results and delivers a copy back to A for further processing.

Our protocol consists of two components. First, the Private

[Fig. 1.] Protocol overview.

Blocking Component aims to reduce the candidate pairs between the records to be matched. This is achieved by converting each of the blocking keys to its phonetic code equivalent.

Phonetic codes are used as a first approximate matching indicator,since they feature some tolerance against typological errors. We inject a random number of records consisting of fake phonetic codes to increase fuzziness, i.e., combinations of phonetic codes not found within the ones created by the actual dataset. These codes are then encrypted using a secure hash function. Identical ciphers that represent phonetic codes, are grouped together. Each group indicates which records should be further examined in more detail for matching.

Detailed approximate private matching by means of the Private Matching Component is performed only between records grouped together by the Blocking Component. Consider the main matching phase, sensitive matching data will be hidden by Bloom Filters. Party A will use a Bloom Filter to replace sensitive data for each field used for matching. For each blocking field B will create candidate pairs. Afterwards, the candidate pairs will be examined for matching using relations R_A^M and R_B^M by Bloom Filter based Levenshtein distance algorithm, resulting in a partial set of matching rows. This set is added to the set of total matching rows. This procedure is executed for each of the blocking fields. For the resulting set B_match of matched rows, B will append its corresponding non-sensitive information to each Bloom Filter and deliver B_match back to A. Finally, A will merge these data with its own.

The aim of the Blocking Component is to make the entire matching procedure more time efficient by reducing the candidate record pairs, while simultaneously maintaining privacy. We employ three levels of security to achieve this: Phonetic encoding,random noise generation, implemented by fake code addition and secure hash encryption.

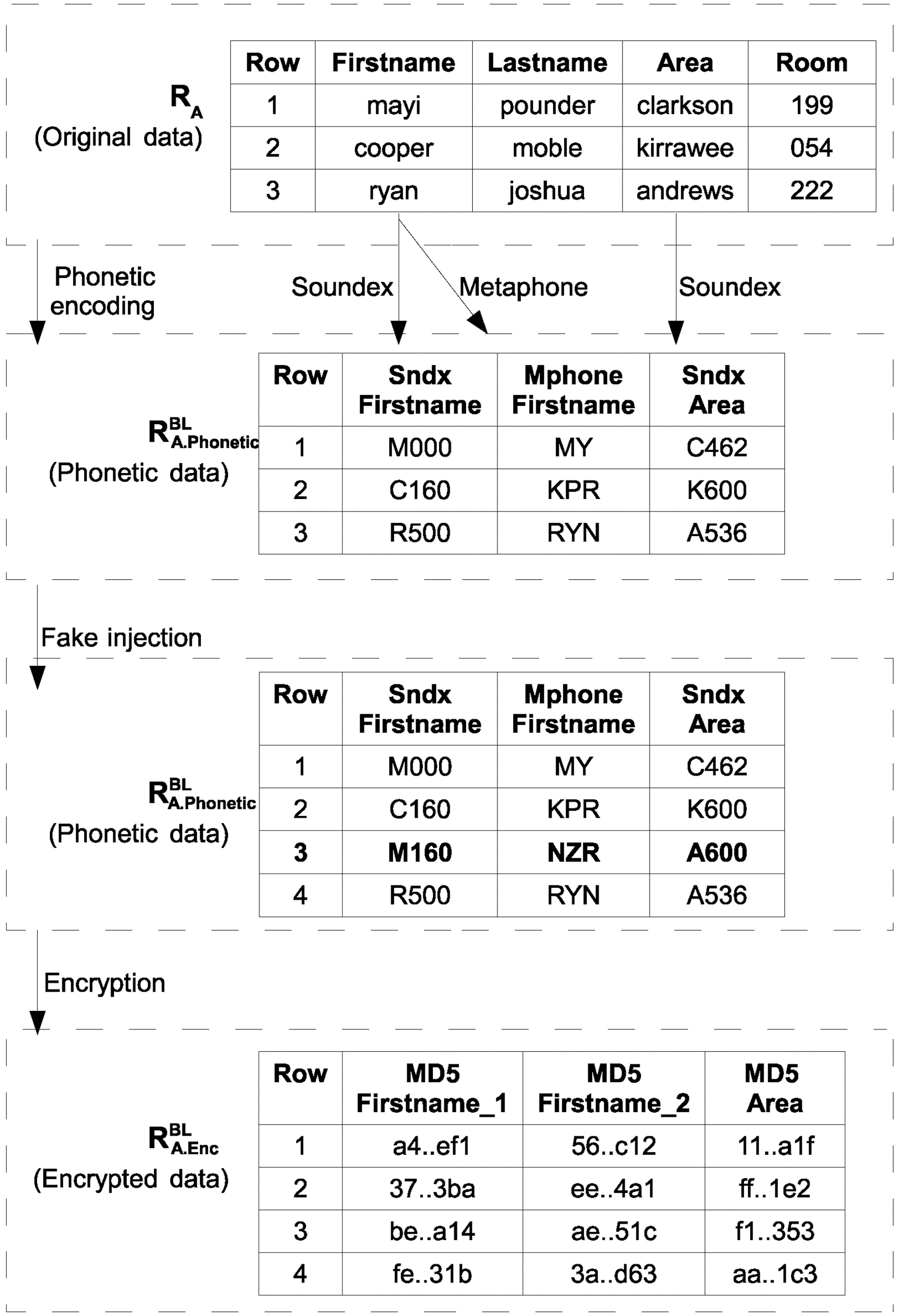
1) Preparation:The entire process can be outlined as follows.One or more phonetic codes are generated at the respective party for each of the fields in RABL and RBBL, resulting in the datasets RA.PhoneticBL and RB.PhoneticBL. Both parties proceed to the same encodings for the same fields. The two new datasets with the phonetic codes may consist of more fields than the initial datasets with the original text fields. This is due to the fact that each blocking key may be encoded with more than one phonetic algorithm.

We follow this process to take advantage of the fault tolerance that phonetic codes exhibit, rendering them appropriate for approximate matching. We use more than one phonetic algorithms for a specific field, since each phonetic algorithm performs better in a different context. Now, a number of fake records comprising phonetic codes are injected into the phonetically encoded datasets. The number and the data of the fakes differ for each of the matching parties. We employ this strategy to artificially increase fuzziness with the phonetics dataset. That is, this approach aims to increase the entropy of the phonetically encoded dataset and as a result, elevate its security.

[Fig. 2.] Blocking preparation at A.

Next, each field belonging to R_A.Phonetic^BL and R_B.Phonetic^BL is encrypted by the respective party using the same secure hash function, resulting in relations R_A.Enc^BL and R_B.Enc^BL respectively.These relations consist of the same number of fields with the relations holding the phonetic codes. Encryption is performed to both ensure confidentiality during transmission and that during the blocking phase the actual data will not be inferred from their phonetic equivalents, since a single blocking field may have many phonetic transformations featuring high entropy.

We will clarify our approach based on the example data in Tables 1 and 2. Fig. 2 illustrates the preparation for the private blocking step in party A. In our example, we will use fields(Name, Area) for blocking. For Name, we will use Soundex and Metaphone for phonetic encoding, while for Area we will only use Soundex.

First, all data within the blocking fields will be transformed to their phonetic equivalents. At this point, it is useful to point out the importance of using different phonetic algorithms over a single blocking field. Considering, the Name field in both of the datasets we can see that there is a misspelling regarding the name ‘ryan’. It is spelled correctly in the third row of Table 1,while there is a misspelling in the first row of Table 2. The phonetic encodings of these two versions using Metaphone are‘RYN’ and ‘RN’ while Soundex produces ‘R500’ for both versions.It is obvious that using a single phonetic algorithm, Metaphone in this case may lead to missing matches. Next, fakes are injected and finally, all phonetic codes are encrypted using a secure hash function. We selected MD5 for this example. The same operations take place at party B. The same set of fields is encoded using the same phonetic algorithms, fakes are injected and then all records are encrypted using the same secure hash function.

2) Private Blocking: After both parties complete this procedure,party A transmits the dataset consisting of relations RA.EncBL and RABL to party B. Now, for each of the blocking fields a multi pass approach is followed. As suggested in [38], datasets RA.EncBL and RB.EncBL are concatenated into a single dataset RBL. This dataset is sorted over the first blocking field that is scanned and sets consisting of identical ciphers are formed. Records within each resulting set are examined with each other within the Private Matching Component. The occurring matching records set is added to the total matching records set that is initially empty.This procedure is repeated for all blocking fields, so that after each pass on a different blocking key, new records are added to the total matching records set.

The Private Matching Component is responsible for offering elaborate and accurate approximate private matching. It utilizes a secure version of the Levenshtein Distance algorithm that we have developed to achieve this. To the best of our knowledge,distance based matching algorithms share some common characteristics to operate properly. First, the position of each character within a string has to be known. Second, the size of both of the matching strings has to be known to evaluate the various distance metrics. These two parameters play an important role in our implementation. Considering the example scenario presented previously in section 3, A and B will agree to merge their data using fields Name, Lastname and Area that will comprise the matching relations and .

1) Preparation: We have developed the following methodology to be able to use such characteristics. For each field AiM each of its characters is extracted. Each of the characters is appended with a number indicating its position within the string resulting in tokens, consisting of a letter and a number indicating the position of this character within the original string. Next,every token is encoded within a Counting Bloom Filter. We prefer a Counting Bloom Filter, to have exact knowledge of the number of elements inserted. This is achieved by summing the bits of the filter that are set. This number is equal to the string length of the original field AiM.

[301] Algorithm 1. Secure edit distance

Algorithm 1. Secure edit distance

To be clearer regarding this part of our approach, consider the first row of Table 1 where data from party A are stored.Applying our methodology to word ‘mayi’, we get four elements:{m1, a2, y3, i4}. Each of these elements will be inserted into the Counting Bloom Filter. After insertion, the sum of bits set by the filter will reflect the number of elements inserted,which in this example equals 4.

A separate filter is used for each field in each row of the matching dataset. After all fields are converted, the matching dataset is transformed to a dataset consisting of Counting Bloom Filters, one for each field of each row. This dataset,which will be referred to as ABloomM together with RA.EncBL, is transferred to party B. It is worth mentioning that this procedure is followed by party A, no matter which distance metric will be used for matching evaluation.

2) Private Matching: Each of the blocking passes occurring within the Private Blocking component results in sets of candidate matching records that according to our protocol will be compared using some distance metric. We will assume the Levenshtein Levenshtein distance metric, modified for our purposes, to better illustrate our approach. Algorithm 1 displays the modified version to be used with Bloom Filters. The changes to the original algorithm are very limited. Specifically, in line 1, a Counting Bloom Filter is used, instead of providing a second string as input. Next, lines 10 and 11 describe that to each character of the known string, its position within the string is appended, and this token is examined for membership against the filter, instead of comparing characters at specific positions as in the original algorithm.

An example will help clarify our approach. Let us consider the case that a blocking pass over the Name field has brought near records 1 from A and 2 from B, as illustrated in Tables 1 and 2. When applying Algorithm 1, s = ‘maya’ and b equals to the bloom filter holding elements {m1, a2, y3, i4}. Each character of s is extracted and its position is appended to it. Then, the resulting token is checked against the filter: ‘m1’, ‘a2’, ‘y3’ are found in the filter, while i4 is not. The result of the algorithm is that the Levenshtein distance equals 1.

In this section, we will provide detailed analysis regarding operations taking place at both the Blocking and the Matching Component. The evaluation is made in terms of efficiency and complexity and in terms of protocol security.

It could be argued that the blocking approach could be used as the main matching procedure, omitting the matching component.However, phonetic codes do not offer detailed matching,leading to increased number of mismatches, having simultaneously increased sensitivity to specific alterations. This renders them unsuitable for detailed matching evaluation.

The use of blocking is essential for the performance of the matching procedure, since it reduces the matching space. Sorting each field of R^BL; requires O(nlogn) and scanning O(n) operations,reducing the candidate pairs significantly. Comparing all by all matching fields would require O(n²) comparisons. The decreased complexity of our approach allows applying the blocking passes more than once with different blocking keys.

We will present an analysis focusing on two aspects, the information gained by each of the data holders and the information gained by a possible eavesdropper over the transmission channel, to evaluate the privacy offered to the integrated data by our protocol.

1) Privacy during Transmission: Private data belonging either to the matching or to the blocking datasets are encoded using a secure hash function. Therefore, if an eavesdropper gained the linkage file, the difficulty to infer information stored in the Bloom Filters is equivalent to the difficulty of breaking the secure hash function. Moreover, the attacker should be aware of the key used in the hash function. Therefore, the attacker should pose a brute force attack to identify the hashing key used and the type of matching algorithm used, since all data are broken into tokens depending on the agreed matching technique.

2) Privacy at the Dataholders: We have assumed that both of the data holders follow an Honest But Curious (HBC) behavior[39], trying to infer knowledge by any available information.We will evaluate the privacy of our approach using the metric of Information Gain. Information Gain is closely related to Entropy.The amount of information in a message is formally measured by the entropy of the message [40]. The entropy is a function of the probability distribution over the set of all possible messages.The entropy of a discrete random variable X is defined as:

Practically speaking, the measure of entropy provides a measure of a set’s predictability. Low entropy of X means low uncertainty and as a result, high predictability of X’s values.Similarly, the conditional entropy of a discrete random variable Y given the value of the discrete random variable X, H(Y'X) is defined as:

Empirically, the notion of conditional entropy aims at quantifying the amount of uncertainty in predicting the value of discrete random variable Y given X.

Information Gain between the discrete random variables Y, X is defined as

Information Gain is a metric to assess the difficulty of inferring the original text (Y), knowing its enciphered version (X), or that is, how the knowledge of X’s value can reduce the uncertainty of inferring Y. Lower Information Gain means that it is difficult to infer the original text from the cipher. In Section VI,we compare the incurred Information Gain in both the Blocking and the Matching Components to the performance of a rival private record matching algorithm.

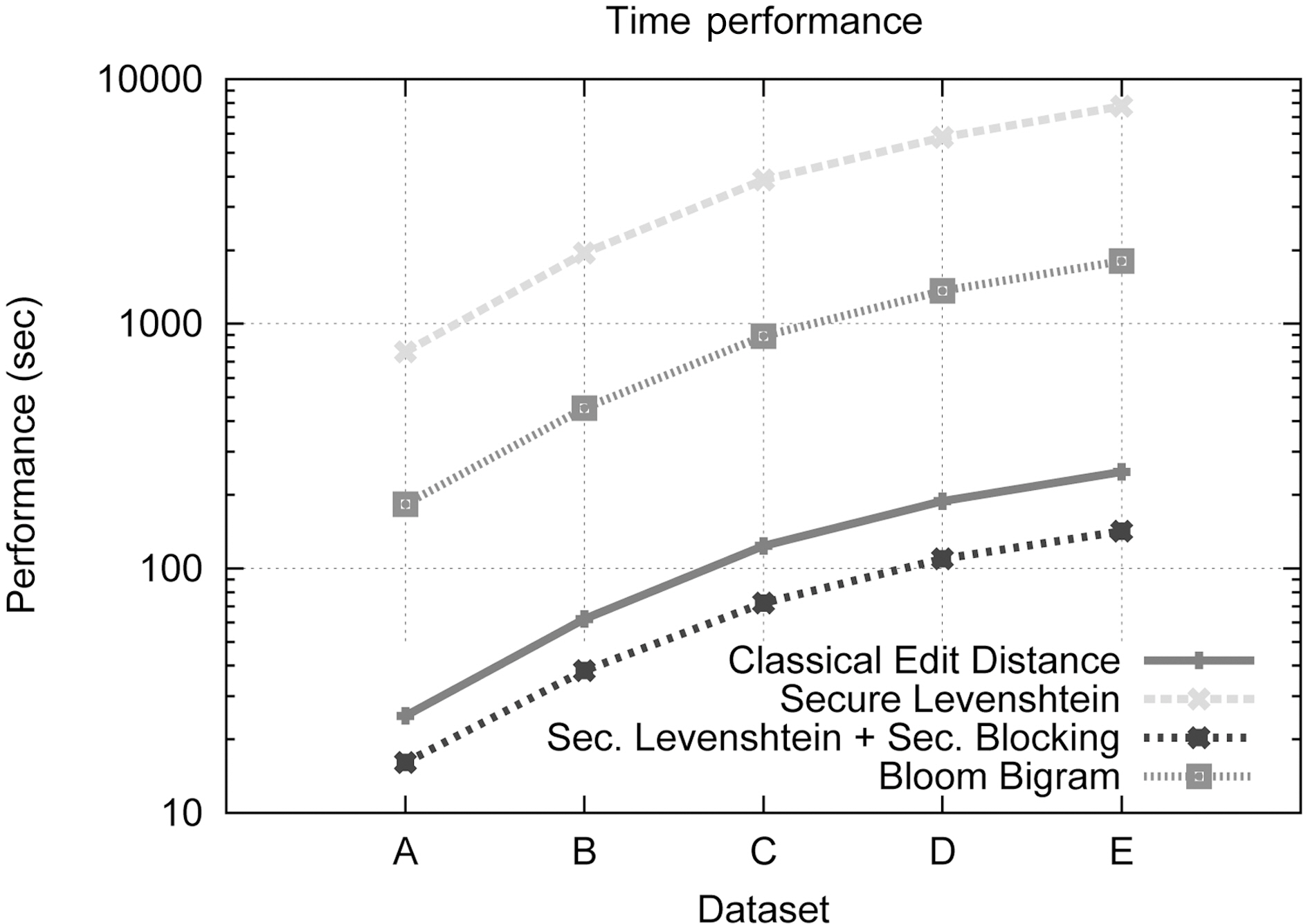
In this section, we provide experiments that prove the effectiveness,the security and the high performance of the proposed framework. We will evaluate the performance of our method in terms of time execution and matching accuracy and compare the results to the performance of the original Levenshtein Distance[3] method and the Bloom Bigram method introduced in [35].

In our experiments, we will evaluate four methodologies to compare them. First, we consider the original Levenshtein method for reference purposes only. The secure Levenshtein Distance method used in the Private Matching Component of our framework will be the second to evaluate. Of course, we will examine the behavior of the fully deployed framework we propose, consisting of the Private Blocking Component and the Private Matching Component. This is displayed in the graphs as ‘Sec.Levenshtein + Sec. Blocking’. Finally, we will use the Bloom Bigram algorithm as a rival to our framework comparing its security, performance and matching accuracy.

We have used in these experiments the bare minimum of the Blocking Component i.e., without injecting any phonetic codes to be fair. In this way, we will be able to assess the minimum security offered by the Blocking Component, without affecting matching accuracy. The fact that the injection of fake phonetic codes does not affect matching accuracy is indicated in [20].

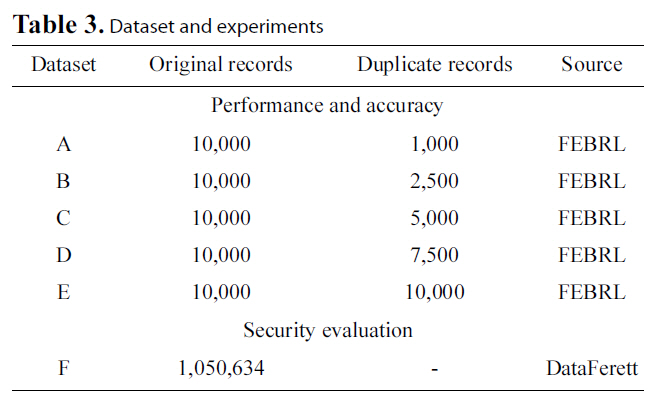
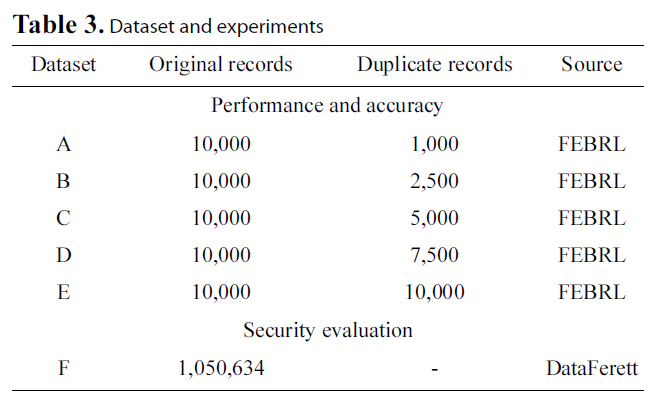
We employed two different data sources to conduct our experiments. We used synthetic data generated by the FEBRL[14] data generator for our performance and accuracy experiments and real world data deriving from the DataFerrett [41]utility for our security evaluation. We used FEBRL to take advantage of its ability to generate random datasets, but also due to its feature to create duplicates of these datasets with a variety of error types. The types of alterations created in duplicate datasets range from simple character deletions, replacements or insertions, to field transpositions and nickname transformations (e.g. “Vanessa”, “Nessi”).

Particularly, we created five different datasets (A-E), as illustrated in Table 3. All these datasets have identical schemas but hold different data. For the duplicates dataset, we required that errors will follow a uniform distribution, with up to 1 error per matching field. The database created by FEBRL has the following schema: Firstname, Lastname ,Street Number, Address 1,Address 2, Suburb, Postcode, State, Date of Birth, Age, Phone Number, and Socsecid. We will be using the set {Firstname,Lastname, Area, Address 1} as blocking fields and the set{Firstname, Lastname, Area} as matching fields. The reason for using DataFerrett was to be able to assess real world data distributions to extract safe conclusions regarding the security of our approach. Specifically, we used data derived from the Historical Census Data from IPUMS 1920 General Sample forming dataset F, as illustrated in Table 3. From the schema of this dataset, we used the following field set: Firstname, Lastname,and Address.

We used MD5 to construct all the methods requiring Bloom

[Table 3.] Dataset and experiments

Dataset and experiments

Filters. Each of the Filters consisted of 900 bits, and four different hash functions. An Intel Core2Duo T5550 was used featuring 2GBs of physical memory for all of the experiments. Data was stored in a MySQL 5 database. All algorithms were materialized in Java 6.

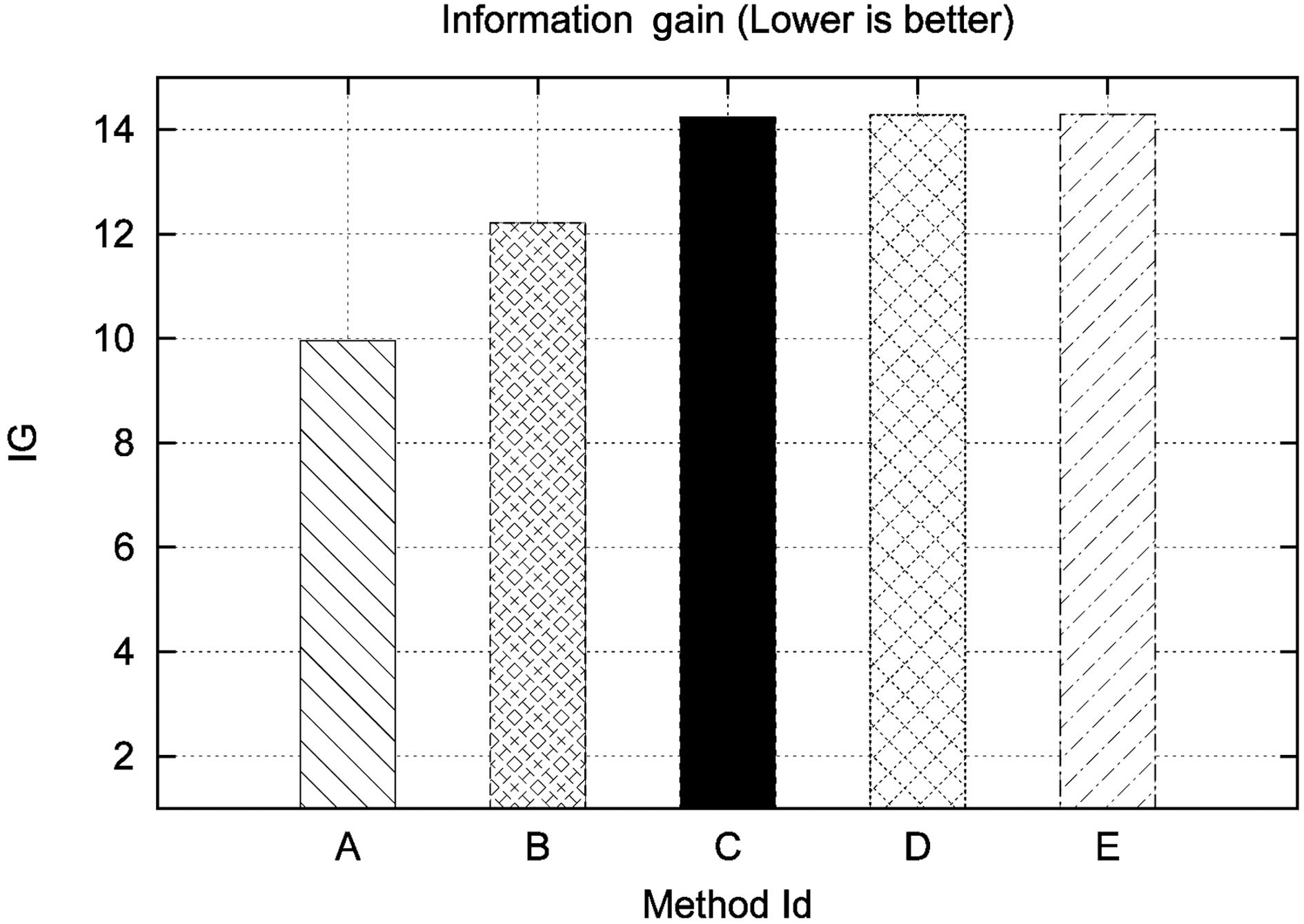
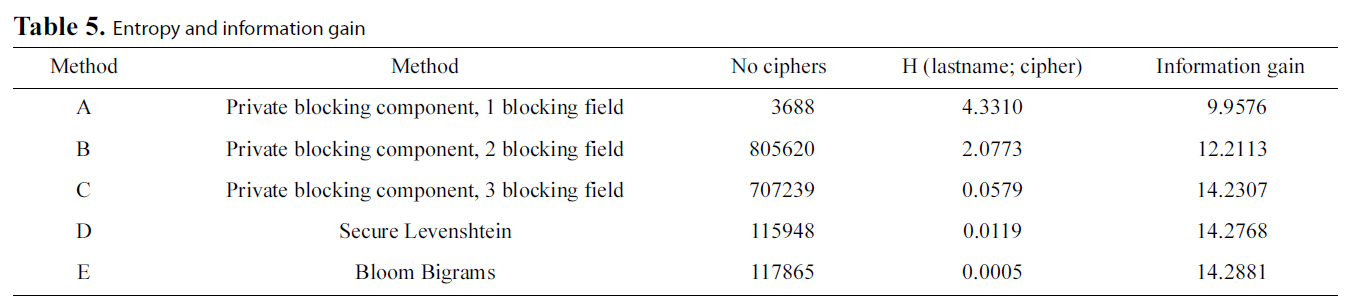
This set of experiments aims at evaluating the security offered by the privacy-preserving methods in our test bed. As such, the original Levenshtein Distance algorithm will not participate in this metric. Moreover, we will separately examine the Private Blocking component and the Private Matching component to be more detailed with our analysis. Specifically, regarding the Private Blocking component, we will present results ranging from one to three blocking keys. These are represented in Table 5 and in Fig. 3 in rows 1 to 3 having respectively Method Ids A to C.

The methodology followed for this set of experiments is as follows. We measure privacy in terms of Information Gain, as

[Fig. 3.] Information gain (IG) comparison.

[Table 4.] Sample query for entropy evaluation

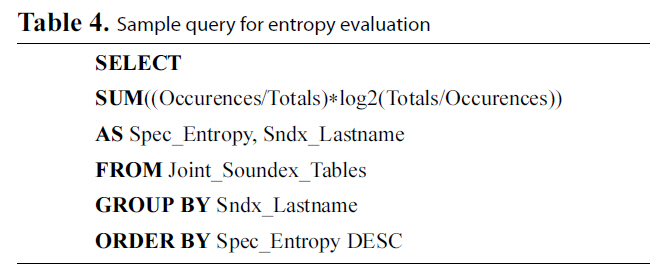
Sample query for entropy evaluation

[Table 5.] Entropy and information gain

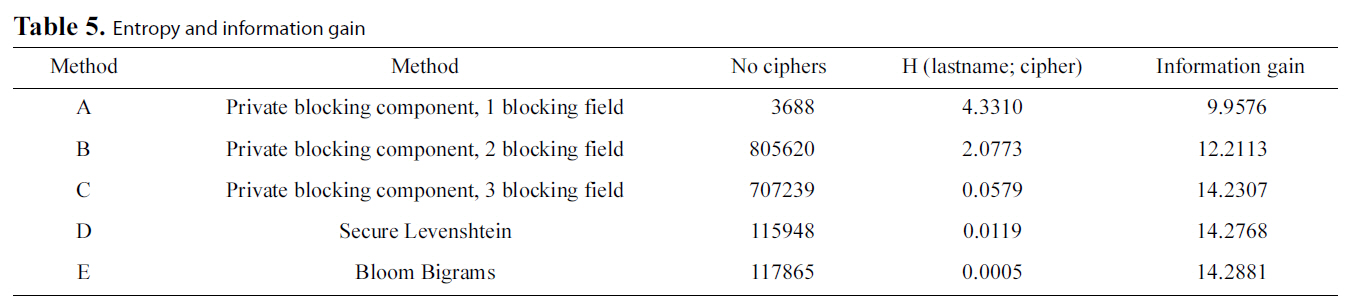
Entropy and information gain

explained previously. We used dataset F to perform our evaluation.Specifically, the resulting figures concern calculations over the ‘Lastname’ field of dataset F. We initially encrypted the ‘Lastname’ field of the dataset using each of the three methods following to evaluate the Information Gain metric for each case. We also used blocking sets {Lastname, Firstname} and{Lastname, Firstname, Address} for the Private Blocking component.All calculations necessary for our security analysis were performed using SQL queries, as in the one displayed in Table 4.

It has to be clarified that in the case of the Soundex method,the results refer to the plain text version of Soundex. This is due to the fact that during blocking, information is revealed in the form of phonetic codes. Party B retrieves phonetic codes, even for records that will not be matched by the Private Matching Component due to the nature of blocking itself. Therefore, it is important to calculate the impact posed to security by our approach.

The results of our experiments indicate, as expected, that the secure Levenshtein Distance approach (illustrated by D) is almost equally secure with Bloom Bigrams (illustrated by E),since, for the same dataset, the amount of information inferred in both cases is practically equal. This is due to the fact that both approaches use the same medium for encryption, i.e.,Bloom Filters.

However, the most interesting result regards the security performance of the Blocking Component. It is evident from Fig. 3 that in this case, statistically speaking, it is much more difficult to infer the original text from the Soundex code than both the Bloom Bigram and secure Levenshtein approaches, even in the case of using two blocking fields. Finally, using three blocking fields proves to be as secure as using the Bloom Bigram Field.

The reason for this is twofold. First, data undergoing the Soundex transformation suffer some information loss, due to the algorithm’s nature. Second, many strings may be mapped to the same Soundex code. Conversely, Bloom Filter based approaches result in a much greater number of ciphers of the original text. All these results are detailed in Table 5.

Additionally, someone might argue that if party B had a plaintext list with the original names, it would be able to infer information combining the plaintext with the phonetic code.However, this is not exactly the case. Observing the last column of Table 5, we can see that the information gain, even when using three blocking keys (which in our case is a candidate key for our schema) has lower information gain compared to Secure Levenshtein and Bloom Bigrams.

This result seems awkward at first sight but it is totally explicable considering the properties of phonetic encoding algorithms,since phonetic codes do not feature one to one mapping.

[Fig. 4.] Time performance comparison.

Consider the following case. Someone has a Soundex code and a plaintext that may produce this phonetic code. Even in this case, it is not 100% sure that the given phonetic code refers to the plaintext. For example, both “Smith” and “Sandy” share the same Soundex code, S530.

It is evident that using more blocking fields increases the probability of compromising privacy, but not significantly.Thus, even in the case of three blocking fields, the probability of breaking privacy is marginally lower compared to methods D and E.

This set of experiments aims at assessing the performance of our complete framework in terms of execution time and comparing it to both the classical Levenshtein Distance and Bloom Bigrams. We also employ the Private Matching component alone to illustrate the necessity of the blocking step. Fig. 4 compares,using a logarithmic scale, the performance of all the aforementioned methods. As can be seen, our private record linkage framework outperforms both classical Levenshtein and Bloom Bigrams, despite the overhead induced by the cryptographic algorithm used. This clarifies the benefit posed by the Blocking Component. It compensates for the encryption burden,and further improves execution performance.

The aim of this set of experiments is twofold. First, we wish to assess the correctness of the secure Levenshtein Distance algorithm we propose. Second, we aim to evaluate the matching accuracy of our private matching framework compared to the original Levenshtein Distance algorithm and Bloom Bigram approach.

We will examine the matching performance of the framework we propose from two aspects. The first regards the behavior of the algorithms for a given matching threshold. That is for distance based algorithms, Edit Distance of 3 and for Bloom Bigrams Dice Coefficient of 0.3 (Fig. 5).

At this point, we consider it necessary to state an interesting detail. Selecting a appropriate matching threshold for the Bigram

[Fig. 5.] Blocking keys time performance.

based approach was tricky, since the Dice Coefficient metric,as presented in [35], depends on the size of the Bloom Filter. As such, this method required some time to properly calibrate the threshold, given our Bloom Filter setup. Conversely,the method we propose is based on the widely used Levenshtein Distance metric that is much easier to calibrate. However, we will not delve into more detail, since this issue goes beyond the scope of this paper.

We employ the Precision, Recall, and F-Score metrics,widely used by the information retrieval community, to evaluate our results. Precision is defined as the number of relevant records retrieved by a search divided by the number of records retrieved by that search, and Recall is defined as the number of relevant records retrieved by a search divided by the number of existing relevant records (that should have been retrieved). FScore is the harmonic mean of precision recall and defined as

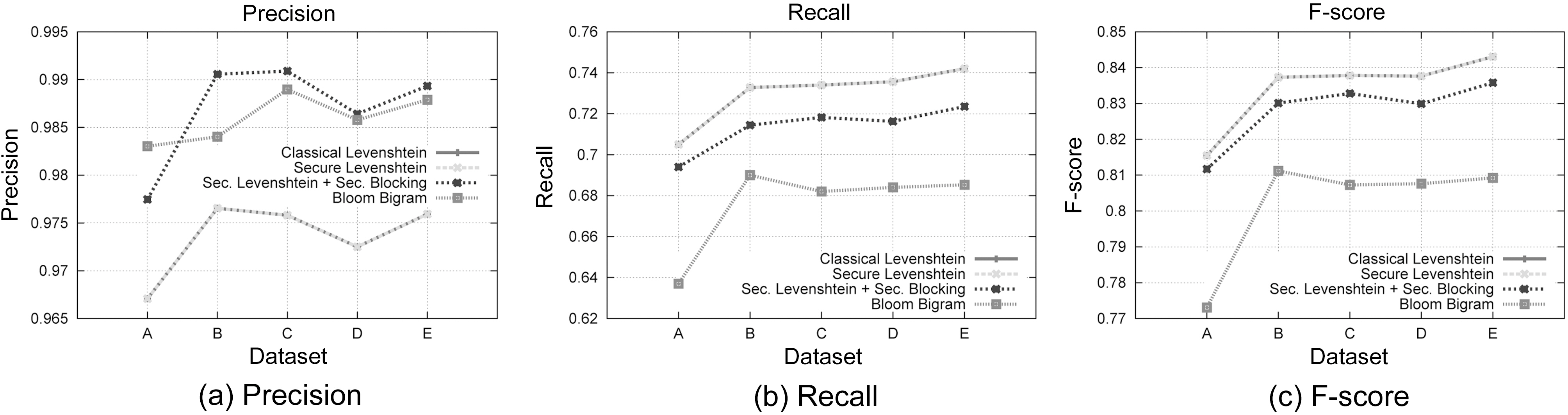
Regarding the first aspect of our results, we can assess that our private record linkage framework outperforms classical Levenshtein Distance in terms of Precision, as shown in Fig. 6a,while it features slightly lower Recall, as shown in Fig. 6b.Higher Precision occurs due to the Blocking Component, since only records with similar phonetic encoding are examined for matching. Conversely, lower Recall is a side effect of the sensitivity of Soundex to alterations of consonants in the blocking fields. Thus, a totally different Soundex code is generated, leading to lower chances of matching. The fact that our suggested method exhibits similar overall performance to the original version is illustrated by the F-Score metric in Fig. 6c. We also observe that the secure Levenshtein Distance algorithm we propose behaves identically to the original version, a fact that proves its correctness. Moreover, we deduce that the differences in Precision and Recall of our framework from the original Levenshtein Distance are due to the blocking approach we used.

It is evident that our method outperforms Bloom Bigrams in all of precision (Fig. 6a), Recall (Fig. 6b), and F-score (Fig. 6c)metrics. This is mainly due to the fact that our approach without blocking, features identical performance to the classical Levenshtein Distance algorithm, in terms of matching accuracy. Not

[Fig. 6.] Results for fixed thresholds.

[Fig. 7.] Precision recall Fscore vs. edit distance.

even the use of the Blocking Component degrades the matching performance. All these results lead us to the conclusion that our proposed method is superior to Bloom Bigrams approach in all cases.

Having established the superior security, accuracy and time performance of our private record linkage framework against its rival, it is now time to explore the details of its behavior. Therefore,in the next set of experiments we have not used the Bloom Bigrams method.

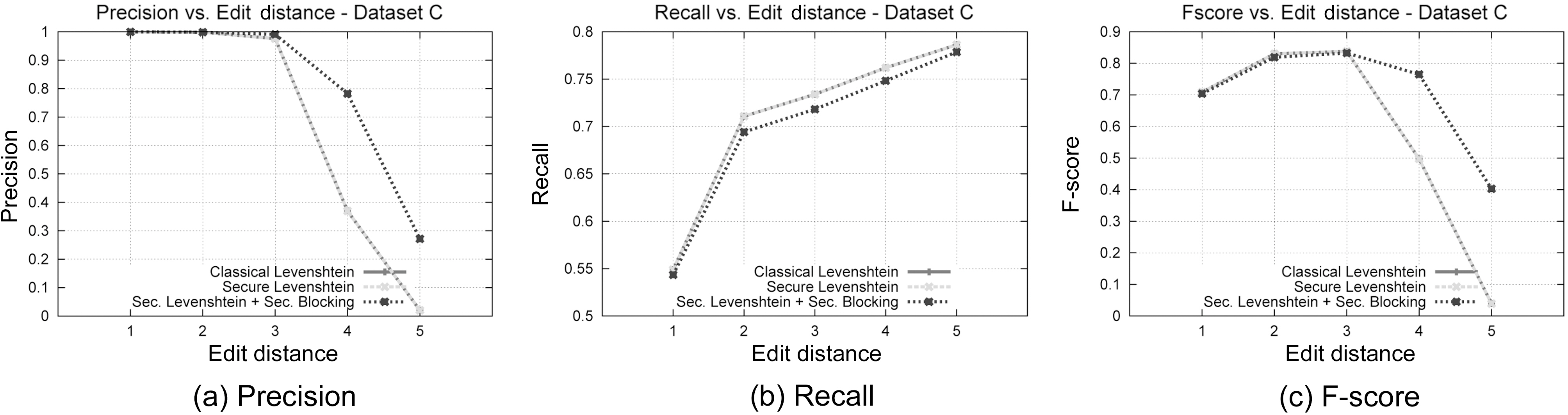
In this set of experiments, we will assess the matching accuracy of our performance, experimenting with a variety of Levenshtein Distance thresholds. We have chosen to use dataset C to reduce the space of possible combinations. Examining our results in terms of Edit Distance, we can see in Fig. 7b that again the proposed framework outperforms the original version of Levenshtein Distance, while it closely follows its Recall performance(Fig. 7b). The stability of the suggested method is more evident in Fig. 7c, where we can see that for lower values of Edit Distance, our method behaves similarly to the original Levenshtein algorithm, while for bigger values it significantly outperforms it. Again, this is due to the use of the Blocking Component, where the phonetic algorithm filters most of the unwanted candidate matches, leading to a reduced matching space. Moreover, this set of experiments assures once more the correctness of our approach, since the results between the classical Levenshtein Distance and the secure version we propose are again identical, irrespective of the edit distance. This leads us to the safe conclusion that this approach can be used instead of the classical Levenshtein Edit Distance algorithm, when privacy is required.

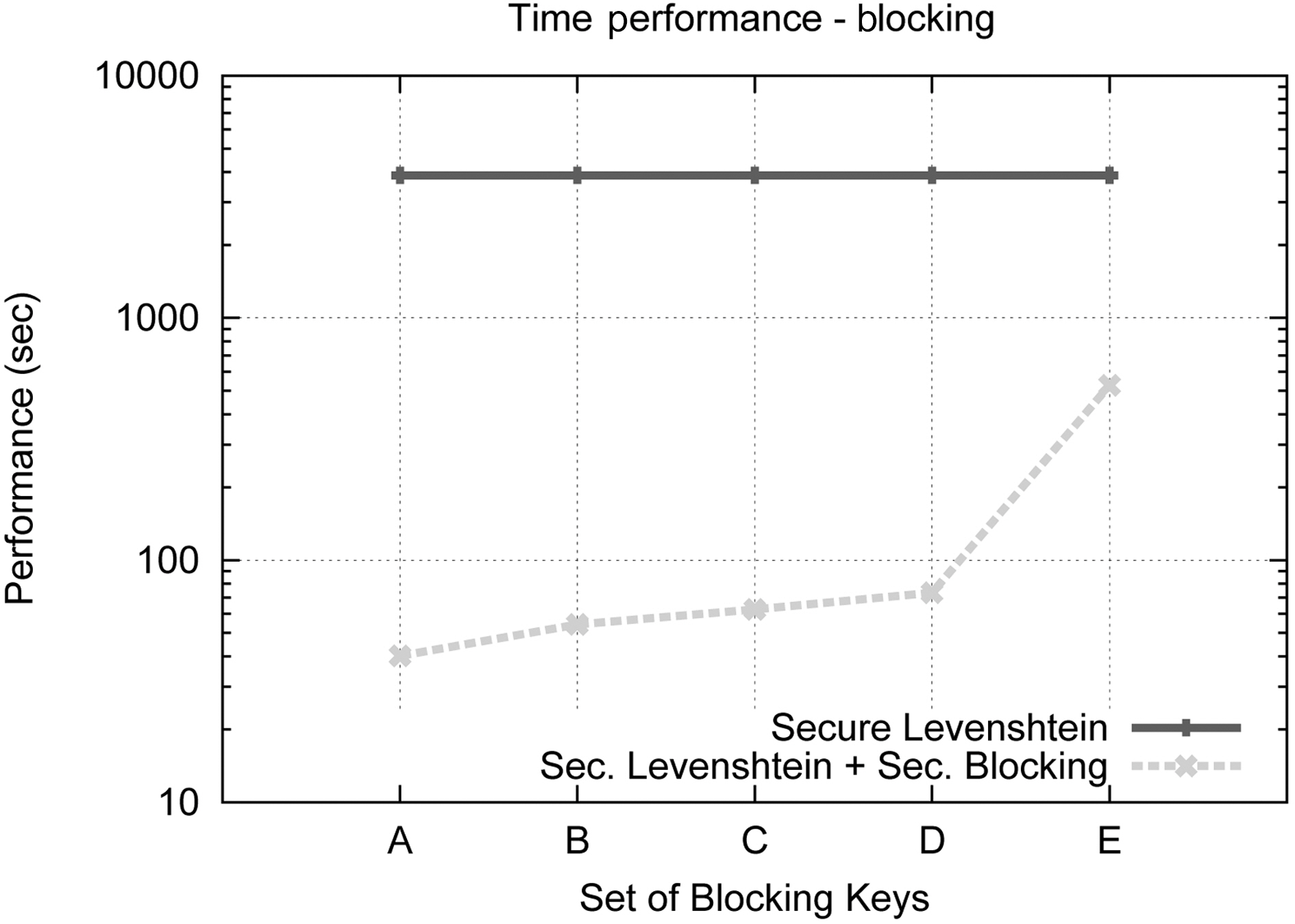
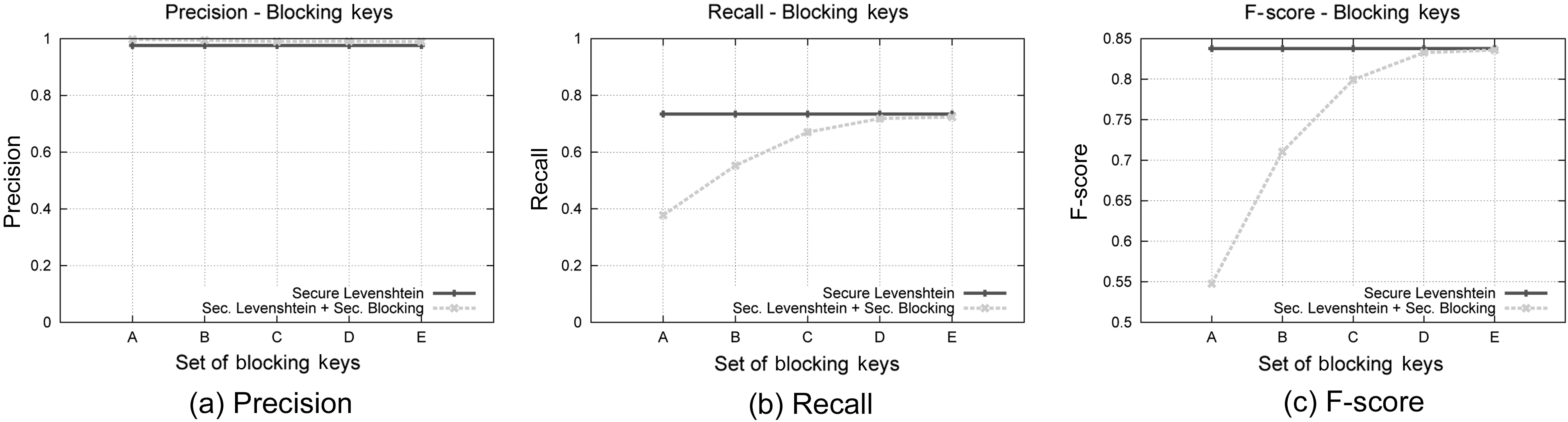
The Blocking Component is an essential part of our protocol,therefore we study separately how its behavior is affected by the blocking keys used. We have used five different sets of blocking keys, as they are listed in Table 6, for this set of experiments.Fig. 5 displays the results concerning the effect on execution time of the various key configurations, while Fig. 8 illustrate the results concerning Precision, Recall and F-Score, for each of the key combinations used. We used dataset C for this set of experiments and considered an edit distance equal to 3. The results are compared to the secure Levenshtein algorithm, which we proved earlier performs identically to its original version, in terms of matching accuracy. It is evident that increasing the number of blocking keys, the quality of results increases, while, as expected,the protocol needs more time to conclude execution. This property

[Table 6.] Blocking key sets used

Blocking key sets used

[Fig. 8.] Precision recall F-score vs. blocking keys.

allows the application of a variety of strategies during the matching procedure between matching accuracy and time efficiency.

In this paper, we presented a novel approach to perform approximate private matching based on the well-known Levenshtein Distance algorithm. Our experiments prove the correctness of our method; it outperforms the original algorithm in terms of execution time, while assuring privacy, and offers almost the same matching performance, which in some cases is superior to the original algorithm.

An important feature of our protocol is that we manage to offer privacy-preserving blocking. Specifically, the Private Blocking component offers the ability to tradeoff matching accuracy and speed, without sacrificing privacy. Depending on the application, we can calibrate the Private Blocking component accordingly.

Our future research directions focus on improving performance in terms of matching accuracy, to overcome the limitations posed by the phonetic algorithms and to explore ways of selecting the blocking keys, in such a way that low execution times are maintained, while matching performance is achieved.Moreover, we are interested in exploring ways to evenly distribute computational burden among matching parties. Finally, we would be interested to modify our protocol to involve more than two matching parties in the computational process.