Photonic crystals (PCs) [1, 2] have attracted increasing attention in the past decade, due to their unique properties and potential applications in wavelength-scale photonic integrated circuits (PICs) [3-5]. These structures are artificial dielectric or metallic periodic structures in which the refractive index modulation causes stop bands for waves within a certain frequency band. These crystals have many applications because of their ability to control wave propagation.The greatest motivation behind these investigations has been the promise that they hold for miniaturizing photonic circuits [6].
Local defects in PCs introduce defect modes within the photonic band gaps (PBGs) [4]. Thus, a point and a line defect can act as a micro-cavity and a waveguide, respectively.The resonant frequency of a defect mode is shifted by changing the size or the shape of the defect [7].
The diffraction limit is a basic principle in classical optics. The emission of light from a structure with a subwavelength feature size will spread into a wide angle range. This is an undesirable property in PICs, because it causes mismatch loss [8, 9]. There have been some methods to obtain beam shaping effects in PCWs [10-23]. One of the methods is to reduce the radii of the surface rods in a PCW in order to create non-radiative surface modes, and then adding a periodic modulated layer of the interface cylinders to support the leaky surface modes [10]. Another method is the reshaping of the surface rods to achieve non-radiative surface modes, and then, for changing the modes to radiative ones, a PC grating layer with a row of rods with the same shape PC rods but different lattice constant is added. In this beam shaping mechanism, the added layers help to induce the electromagnetic waves at the surface to radiate their energy into a beam just a few degrees wide [26]. A directional emitter can also be achieved by covering the termination of a PCW by a self-collimating PC, in which the interference of the multiple self-collimated beams excited by the waveguide reshape the output beam[27]. Also, in another scheme, a multimode (MM) PCW is terminated by a waveguide array. The output of the MMPCW,regarded as a secondary source, splits into two beams to be launched to the waveguide array. As a result,many split light beams can be generated in the waveguide array by coupling among the waveguides. Hence the interference of these light beams after passing through the system leads to the desired directional emission [32].
Adding a CROW to the end of the PCW can collimate the PCW output lightwave over a wide bandwidth range.These CROWs produce resonant modes, which radiate from the PC structure. These resonant modes and the lightwave emitted from the PCW can be regarded as radiating sources to interfere in free space. The total output field is determined by the vector addition of the fields radiated by the individual sources. To provide very directional patterns,it is required that the fields from the elements of the array interfere constructively in the desired direction and interfere destructively in the remaining areas. The interference produces a directional emitting beam. The mechanism providing a large operational bandwidth is due to the lower
In addition, researchers have introduced some structures for achieving off-axis directional beaming via engineering the PC surface layer [28, 29]. They have also presented some structures to split the output beam of PC into more than one beam in various desired directions, for which the output beam property such as angles, intensities and FWHMs are related to the engineering of the surface layer of the PCs [13, 30, 31]. These structures are very useful beam splitters in PICs to drive output lightwaves to be launched to photonic devices with more than one input or to several devices.
However, due to the impedance mismatch and reflection at the termination of PCWs, some of the reported directional emissions are inefficient and are based on intuition and trial and error without any genuine optimization. So, the researchers have tried to improve the efficiency of the PCW directional emission [14-35].
In many of the proposed methods, a surface layer is formed to excite the non-radiative surface modes, and then another layer is added to convert these modes to the radiative ones. The performance of the directional emission depends mainly on the coupling efficiency between PCW and the surface modes [15, 33]. Also, the coupling efficiency is sensitive to surface layer parameters such as radius,refractive index [13], and lattice period [35]. Further enhancement of the coupling efficiency is possible, if one can optimize the period of the surface cylinders, simultaneously with the other parameters.
Some optimization methods have been used for obtaining the optimized parameters of the termination structure of the PCWs to achieve the most improved directional emission.A PCW with grating-like surface, added for highly-efficient directional emission, has been optimized by the genetic algorithm (GA) method. The interference of the lightwaves emitted from the output of the waveguide and the modes of the grating-like surface is believed to affect the directional beaming of these structures [36].
One of the powerful algorithms that can be employed for optimization of the multidimensional problems of this kind, especially in the domain of computational electromagnetism,is the particle swarm optimization (PSO) method [37-47]. Recently, some different PC structures have been optimized by using the PSO algorithm to evaluate a fitness function [48, 49].
In this paper, we have used the PSO algorithm to optimize the parameters of a CROW in the output surface of the PCW structure [19] to get a powerful directional beam. The paper structure is as follows. In section II, the details of the structure and simulation space will be described. In section III, the PSO algorithm will be explained.In section IV, the beam shaping effects of the non-optimized,1D-PSO optimized and 7D-PSO optimized CROW will be demonstrated. Also, the FWHM and bandwidth of each structure will be derived. The paper will be concluded in section V.
II. DETAILS OF STRUCTURE AND SIMULATION SPACE
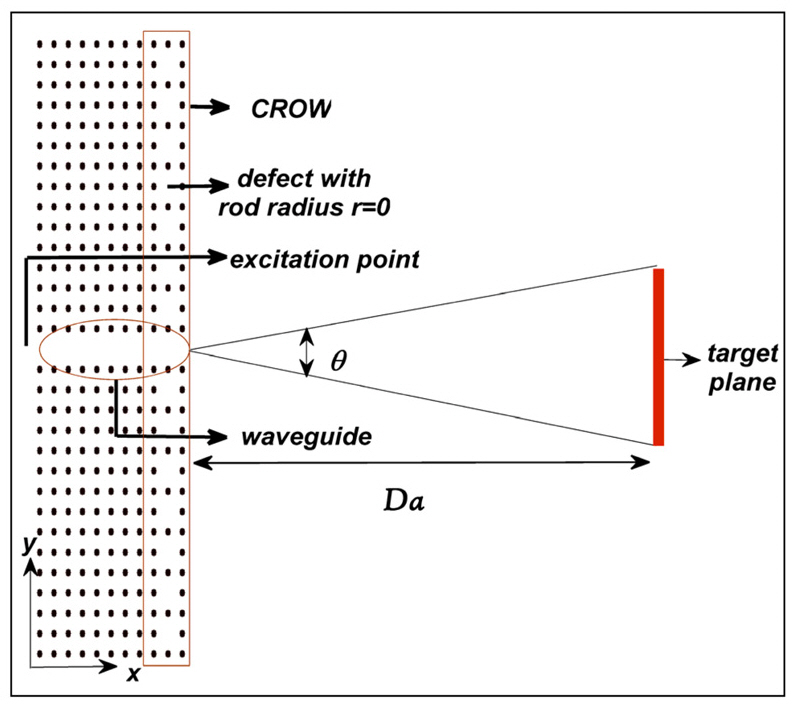
We have considered a PC structure with a square lattice of dielectric rods in air, as shown in FIG. 1. The relative dielectric constant of the rods is 11.56, corresponding to that of InGaAsP-InP semiconductor material at 1.55 ㎛ wavelength [19], and the rod cross-sectional diameter is chosen to be 0.36a, where a is the PC lattice constant. For TM polarization with the electric field Ez parallel to and magnetic field perpendicular to the rods' axis with components Hx and Hy, the PBG of the PC structure, derived by either broadband Gaussian pulse excitation or the plane wave expansion (PWE) method, is in the normalized frequency
range of 0.306-0.439, where
considered the spatial step in the FDTD method to be Δ
The incident lightwave signal is a modulated Gaussian:
where
In this paper, the FDTD software was prepared in C++and MATLAB and was executed on a Pentium IV quad core CPU computer with processing capacity of 2.84 GHz and 3.25 Gb of RAM.
III. AN OVERVIEW OF THE PARTICLE SWARM OPTIMIZATION METHOD
PSO is a stochastic evolutionary optimization method based on the movement and intelligence of swarms proposed first by Kennedy and Eberhart [37].
In this method, the population of potential solutions to the problem under consideration is used to probe the search space. Each particle adjusts its movement according to its own and its companions’ movement experiences.This process is continued until the best solution is achieved[46]. Both genetic algorithm (GA) and PSO are similar in the sense that both are population-based search methods and search for the optimal solution by updating generations.Unlike GA, PSO has no evolution operators such as crossover and mutation. Also, GA and PSO employ different strategies and computational efforts. PSO has been demonstrated to be superior to the genetic algorithm for certain difficult optimization problems [43]. Furthermore, compared to the genetic algorithm, PSO is easier to be implemented and has lower parameters to be controlled. Moreover,researchers have achieved improved and simplified models in the PSO algorithm, for example local PSO and Boolean PSO. However, specialists are trying to find more simplified models. PSO has already given some promising results in the domain of photonics in particular and electromagnetics in general [44-51].
In each PSO problem a “fitness function” is defined to guide the particles through the solution space to that position where the fitness function has its target value. Each particle is treated as a mass-less and volume-less point in a D-dimensional space. The
where
Some experimental results demonstrated that the global best model converges quickly on problem solutions but has a weakness for becoming trapped in local optima, while the local best model converges slowly on problem solutions but is able to “flow around” local optima, as the individuals explore different regions. The global best model is strongly recommended for the single-modal objective functions, while a variable neighborhood model is recommended for the multi-modal objective functions. For the local best model Eqs. (2) and (3) do not alter significantly. But the subscript g (global) is changed to l (local) [40].
When the solution space is discrete, Boolean PSO is preferred, and Eqs. (2) and (3) change by replacing additions and products with exclusive OR and AND operations,respectively. A full description of Boolean PSO and conventional PSO can be found in [44, 50].
IV. EFFECTS OF PHOTONIC CRYSTAL WAVEGUIDE SURFACE PARAMETERS ON OUTPUT POWER
We consider two PC waveguides with parameters described above, without and with CROW surface structure with defect rods diameter of
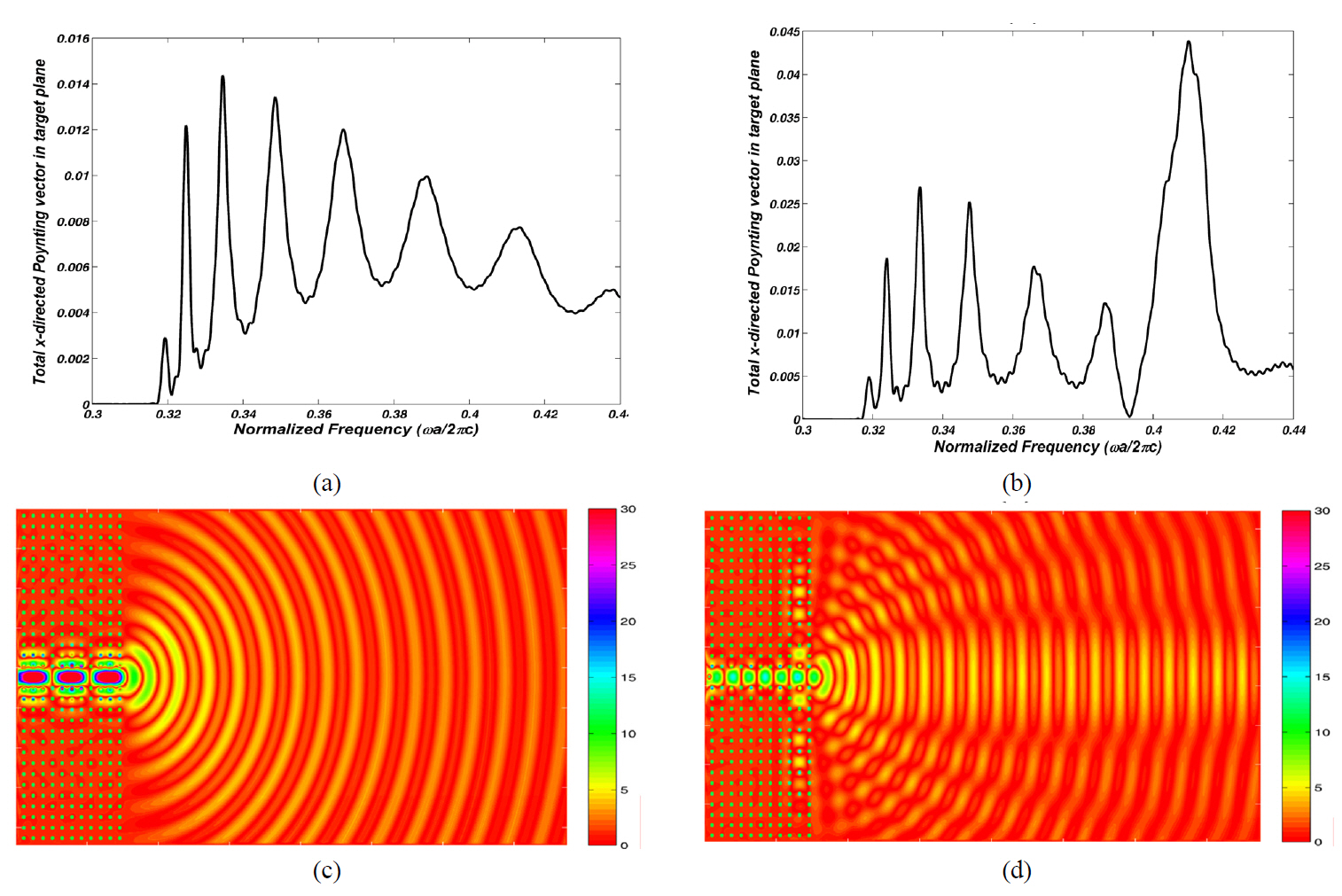
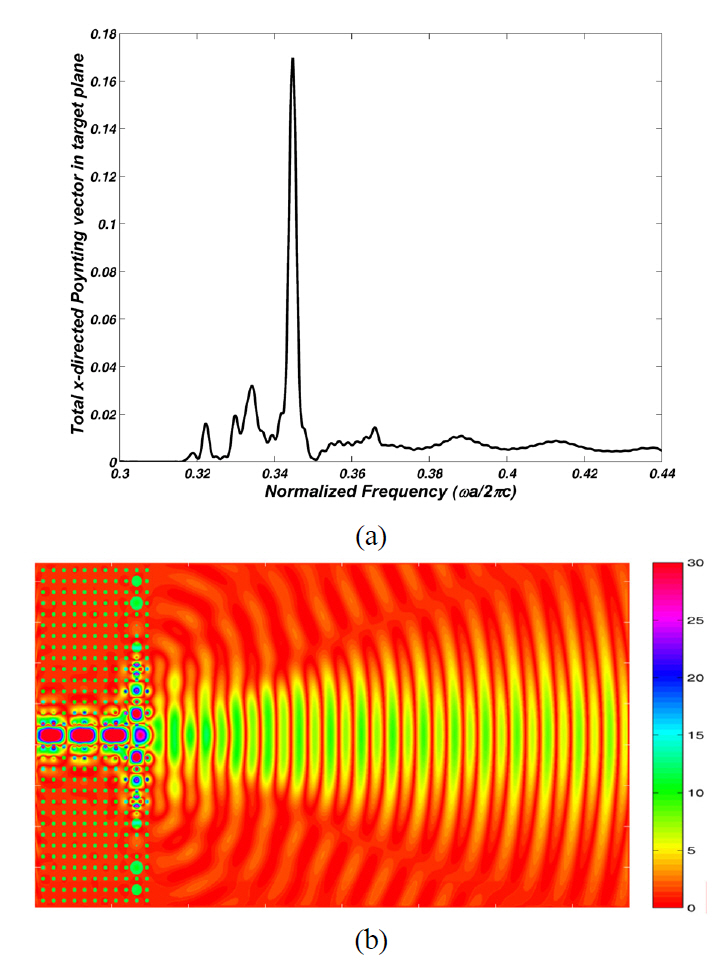
specified bandwidth. FIGs. 2c and 2d show the electric field distributions in normalized frequency of 0.334 and 0.410, for which the maximum power is received by the target plane from the PC waveguides without and with the CROW surface, respectively. As illustrated, the
4.1. Optimization of the Crow Cavity Rods with the Same Diameter
Further improvement of the directional emission of the PCW with CROW structures is possible by variations of the diameters of the defect rods. First, we assume the same defect rod diameter and try to optimize the diameter by a 1D-PSO algorithm. There is a one dimensional solution space that can be searched for the optimum solution by using the PSO algorithm. Since the purpose of the optimization process is to increase the PCW directional emission,we choose the fitness function as the power (x-directed Poynting vector) received by the target plane located at the distance 35a (
In this optimization process the same diameters of 0.21a have been derived for the defect rods. FIG. 3a shows the spectrum of the total x-directed Poynting vector received by the target plane of this optimized structure. As we can see the normalized frequency for which the maximum power is received by the target plane is shifted to 0.344.Since the frequencies have been normalized to the lattice constant a, manufacturers can choose suitable a value to shift the maximum power wavelength to a desired wavelength,say 1.55 ㎛. The maximum power received by the target plane is 2.79 times higher than that of the previous non-optimized structure.
In exchange for the greater power received by the target plane and more intensive beam, the normalized bandwidth of the beam shaping effect decreased from 0.014 to lower than its half amount, 0.0052 which can be deduced by comparing FIGs. 2b and 3a. FIG. 3b demonstrates the electric field distribution in normalized frequency of 0.344.The stronger beam focusing compared to that of the previous structure is obvious.
Optimization of other parameters of the defect rods,such as dielectric constant, was not executed because of the probability of obtaining impractical results.
In this 1D-PSO algorithm we have chosen 80 particles for global best algorithm with acceleration constants c1=c2=1.5, linearly descending inertial weight from 0.95 to 0.2,
The execution time for optimization was 148 hours with the computer described in section II.
4.2. Optimization of the Crow Cavity Rods with Different Diameter
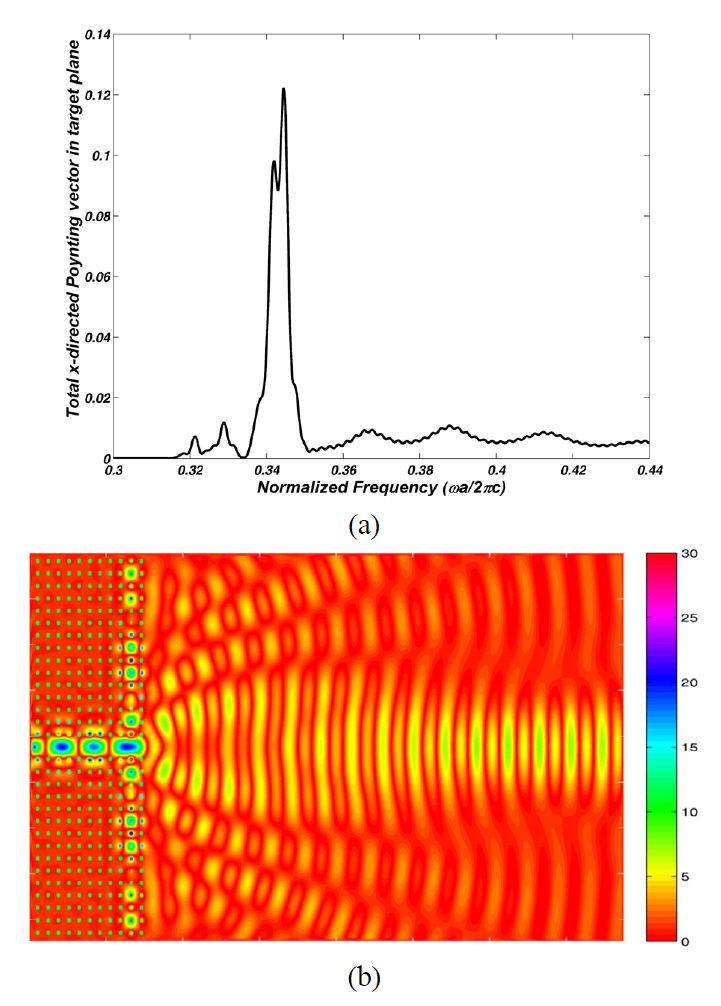
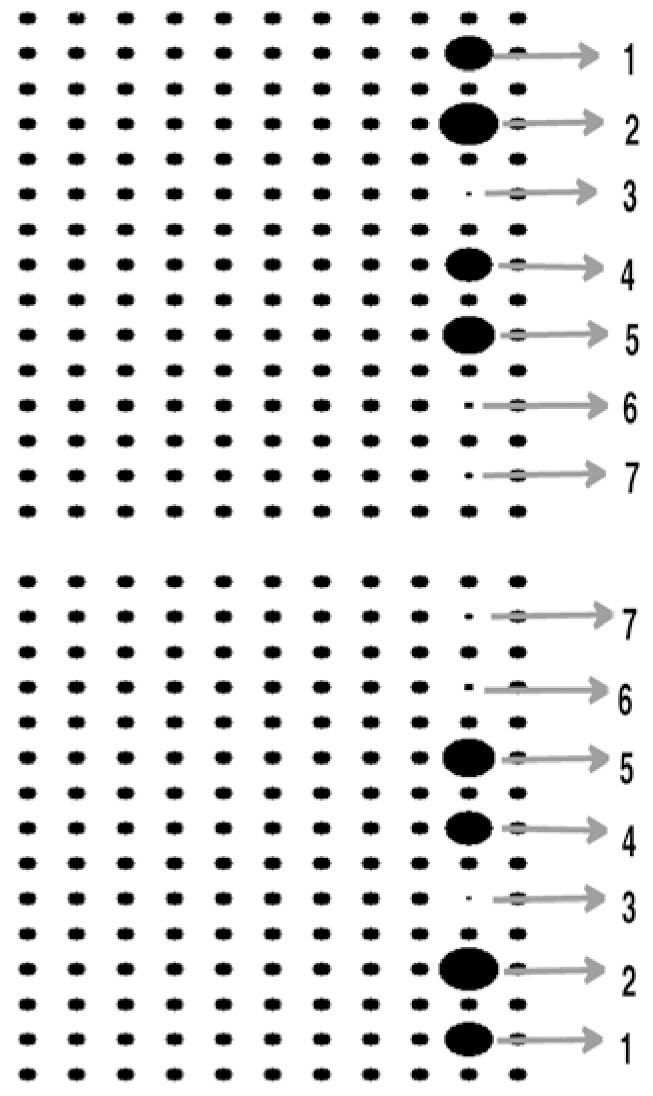
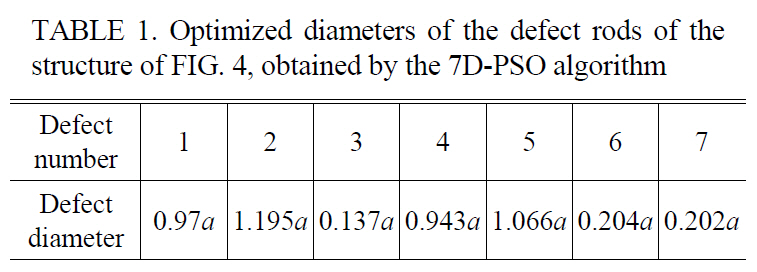
Optimization of the combination of the diameters of the CROW rods can cause better results in the beam focusing effect. Therefore, we have numbered the defect rods consecutively from the top of the waveguide, as shown in FIG. 4. Since this structure has seven resonators in both sides of the waveguide, due to the symmetry of the structure,we have seven defect rods to be optimized. So, we have a seven dimensional (7D) solution space that can be searched for the optimum solution by using a 7D-PSO algorithm.The fitness function is the same as that of the previous subsection. The optimization results for the diameters of the defect rods are given in TABLE 1. FIG. 5a depicts the spectrum of the total x-directed Poynting vector received by the target plane of this optimized structure. The maximum power has been received in the normalized frequency of 0.344. The electric field distribution in this frequency is shown in FIG. 5b. The 7D-PSO optimized structure has caused 3.875 and 1.389 times improvement in the received power by the target plane compared to the previous non-optimized and 1D-PSO optimized structure, respectively.
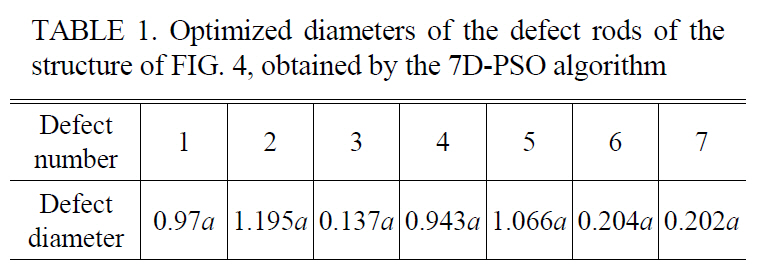
Optimized diameters of the defect rods of thestructure of FIG. 4, obtained by the 7D-PSO algorithm
The angle
Although global best model converges quickly on problem solutions, in this 7D-PSO algorithm, it was not appropriate because of trapping in local optima. So, we divided the solution space of the PSO to six different explore regions to use local algorithm of PSO. In each region we had 70 particles with acceleration constants of c1=c2=1.5, linearly descending inertial weight from 0.95 to 0.4,
In both 1D and 7D-PSO algorithms, the boundary values of the defect rods' diameters and the particles’ velocities have been assigned. The diameters of the defect rods must vary from 0 to 1.64a (2a-0.36a=1.64a) and the velocity of particles must be in the range of [-
The PSO with 25 iterations was sufficient for each of
the explored regions that were simultaneously optimized.The execution time for optimization of each region was about 430 hours with the computer described in section II.
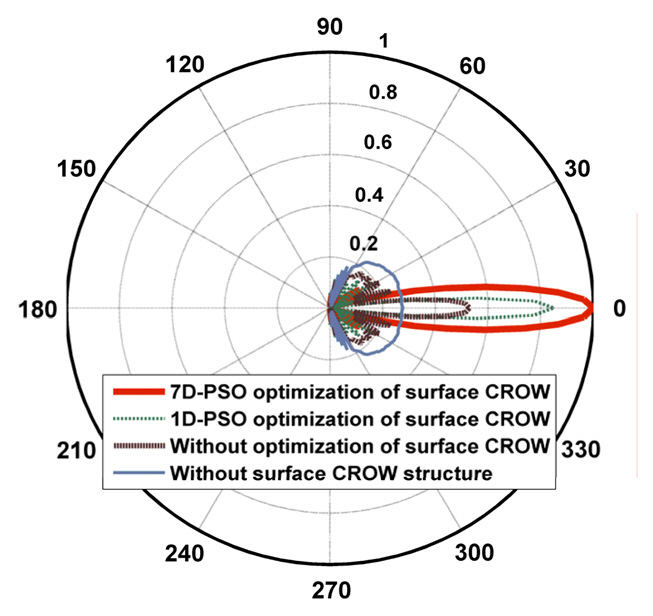
FIG. 6 shows the polar diagram of the normalized electric field pattern in the azimuthal plane at a distance of 35a from the output of PCW for the four analyzed and simulated structures. We can see the beam focusing improvement in each step of the above cases. In each step, the power at the angles out of the specific narrow angle in front of the PCW decreases and their power transfers to the main lobe lying in this specific angle. So, the main lobe becomes very intensive.
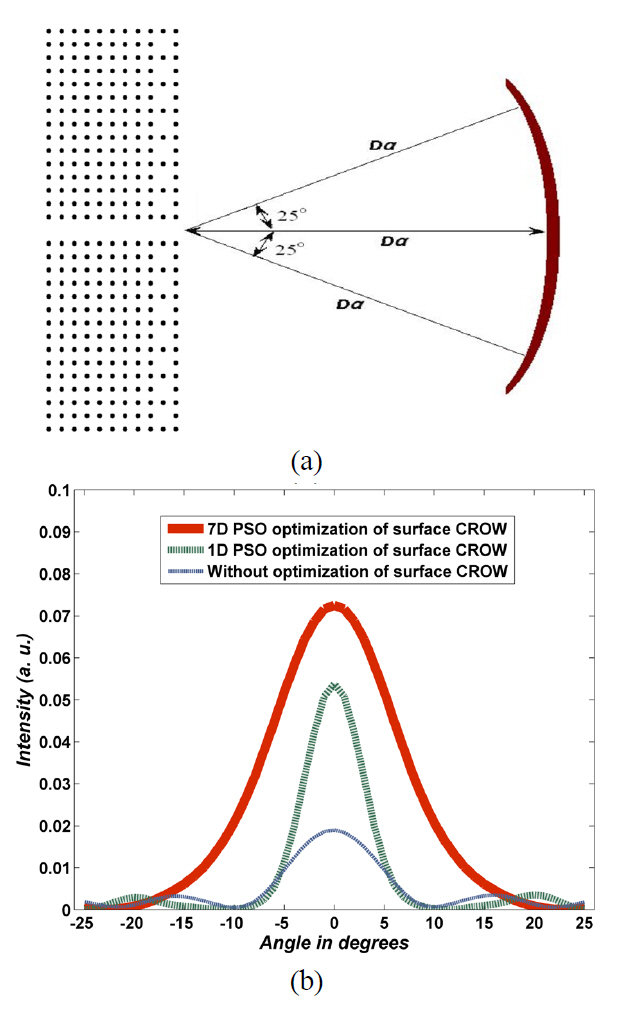
To compare the FWHM of output beams, we measure the Poynting vector in radius direction in cylindrical coordinate system, in the view angle range of -25° to +25°in free space shown in FIG. 7a, the results of which are illustrated in FIG. 7b. Each diagram in this figure has been plotted for the normalized frequency in which the maximum power is received by the target plane of FIG. 1 in each structure. The red (solid), green (dashed) and blue(dotted) lines describe the power pattern in the normalized frequencies of 0.344, 0.344 and 0.410 for 7D-PSO optimized,1D-PSO optimized and non-optimized CROW surface structure, respectively. The blue (dotted) diagram belongs to the structure without optimization which the defect rods diameter are
FWHM of 7°. This FWHM shows a decrement of 1.43 times compared to the non-optimized structure. The increased intensity and beam shaping effect is significant in this structure.In the 7D-PSO algorithm of the red (solid) diagram, all the minor lobes have been eliminated and the main lobe becomes very intensive, but the FWHM is increased to 14°; 1.4 and 2 times increments compared to the non-optimized and 1D-PSO optimized structures, respectively. Although the FWHM becomes higher than the previous cases, the power distribution is very significant in the main lobe and very low (approximately zero) in the angles out of the main lobe.
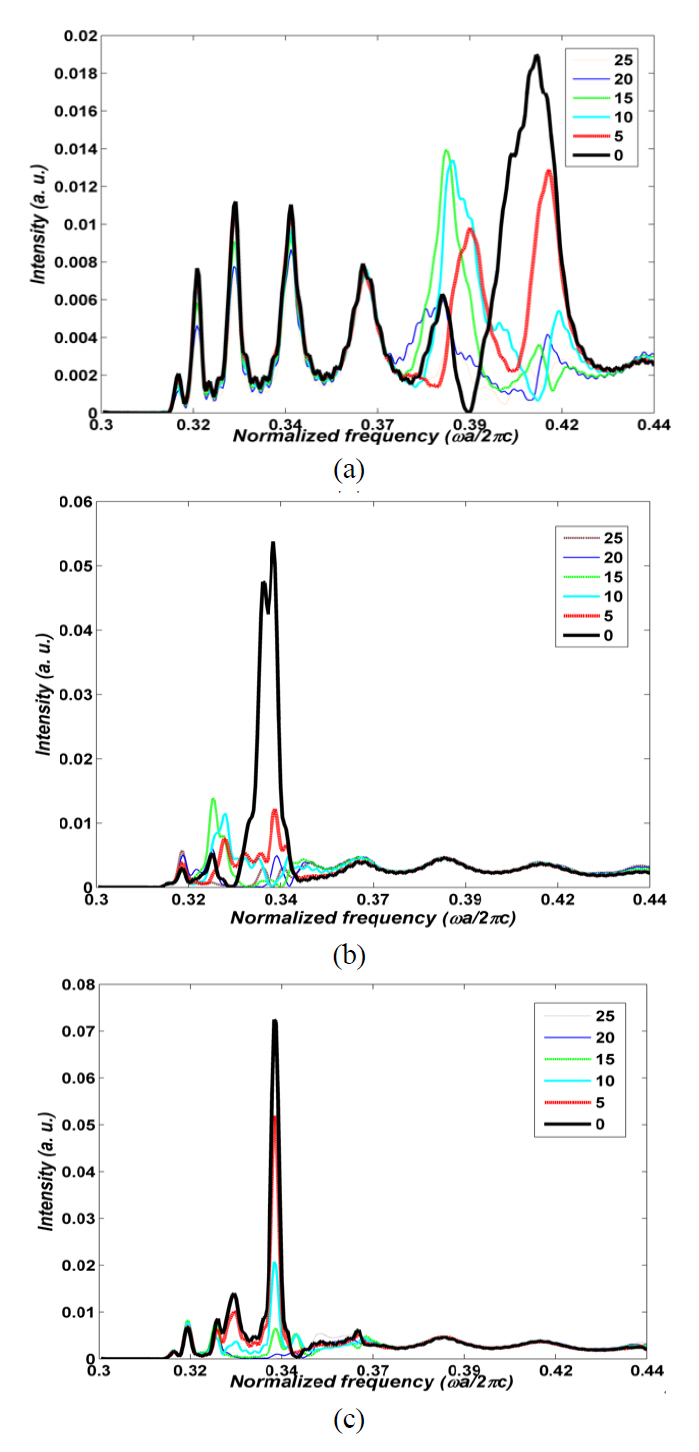
For more study of the intensity, FWHM and bandwidth
of beam shaping of the PCW output, we launch similar pulses to the non-optimized, 1D-PSO optimized and 7D-PSO optimized CROW surface structures. FIG. 8a-8c depict the spectra of
The ratio of the intensities at angles of 5° and 0° of non-optimized, 1D-PSO optimized and 7D-PSO optimized beams in their maximum power transfer frequency are 0.5,0.21 and 0.72, respectively, which confirms that the FWHM of 1D-PSO optimized and 7D-PSO optimized beams are the least and the most, respectively.
FIGs. 8a-8c also show the frequency bandwidth of the higher intensity of detector at 0° angle. These confirm the lower frequency bandwidth of the beam focusing for the more intensive output structure.
In this paper, we have designed two photonic crystal waveguide (PCW) structures with focused output beams in order to achieve more coupling between photonic devices and decrease the mismatch losses in PICs. We have used the particle swarm optimization (PSO) algorithm for PCW terminated by a CROW structure. We could focus some of the powers of the minor lobes to the main lobe by one dimensional (1D) optimization of the same resonator rods diameter. In this optimized structure the intensity calculated by the fitness function of the PSO increases and the FWHM of the main lobe decreases. But there were some undesirable minor lobes that should be eliminated.So, we used 7D-PSO algorithm to optimize the various diameters of the seven resonator's rods. The power of minor lobes became very low and most of the powers were focused to the main lobe. So, the main lobe radiated power became more intensive. But the FWHM of the main lobe increased compared to the non-optimized and 1Doptimized structure. We have also shown that the higher directivity and intensity causes the lower bandwidth, because the directionality and intensity heavily depend on the resonators in the optimized structure. The method can be extended for simulation and optimization of the photonic crystal power splitters and multi/demultiplexers.