The gross primary production (GPP) of forests may function as a terrestrial carbon sink against climate change (Suwa et al. 2006, Canadell et al. 2007, Luyssaert et al. 2008, Saigusa et al. 2008, Lewis et al. 2009). GPP is also a fundamental energy and material source that occurs in forest ecosystems as the result of litter input (Kurokawa and Nakashizuka 2008, Litton and Giardina 2008), and the activity of ectomycorrhiza (Druebert et al. 2009). Recent "ecological scaling" theories have outlined simple relationships predicting ecosystem carbon gain from single leaf photosynthesis (Sellers et al. 1992, Koyama and Kikuzawa 2009, 2010). However, these models are useful for the spatial integration of canopy photosynthesis. To estimate GPP, temporal integration over growing seasons is required (Thornley 2002). In service of this objective, numerical calculations (e.g. Hikosaka 2003) have been applied. However, a simple model for time-integration over the growing period has yet to be developed.
Leaf demography and longevity has been studied extensively in association with whole-plant carbon economy (Chabot and Hicks 1982, Ackerly and Bazzaz 1995, Franklin and Agren 2002, Oikawa et al. 2004, 2008, Reich et al. 2004, Hikosaka 2005, Koyama and Kikuzawa 2008, 2009, Mediavilla and Escudero 2009, Suarez 2010). Mathematical models predicted that higher photosynthetic rates in leaves would result in higher leaf turnover rates, accompanied by reduced leaf longevity (Kikuzawa 1991, Ackerly 1999, Hikosaka 2003). In support of this notion, a negative correlation was observed to exist between leaf lifespan and the instantaneous light-saturated leaf photosynthetic rate (Chabot and Hicks 1982, Koike 1988, Reich et al. 1991, 1997, Wright et al. 2004, Vincent 2006, Ishida et al. 2008, Nagano et al. 2009). Hence, it has been suggested that this lifespan-carbon gain relation can be employed in the development of a quantitative model of ecosystem productivity (Saura-Mas et al. 2009). However, to the best of our knowledge, no study has yet successfully estimated GPP via this relationship.
Kikuzawa and Lechowicz (2006) recently proposed a scheme that predicts GPP over the growing period, using a simple model. In essence, they demonstrated that if the leaf lifespan is a function of the daily carbon gain of that leaf, then the leaf lifetime carbon gain can be viewed as an inverse function of the leaf lifespan. In this paper, we applied this method to estimate the GPP of a temperate deciduous forest composed of Japanese beech (
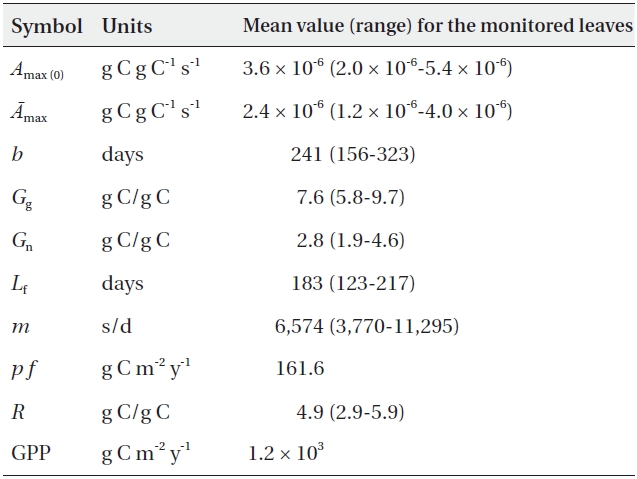
Our model is based on the model described by Kikuzawa and Lechowicz (2006), with some slight modifications. The relevant symbols are listed in Table 1. The two principal assumptions here are as follows: 1) leaf lifespan is determined so as to maximize whole-plant carbon gain, in concert with the numerical model of Kikuzawa (1991) (for a more elaborate version of this model, see Takada et al. 2006). This model was also supported by the empirical data (Kikuzawa and Ackerly 1999). 2) Stand leaf biomass is constant for closed steady-state canopies (Tadaki 1986, 1991). GPP (g C m-2 y-1) is the sum of leaf photosynthesis of all the leaves within a stand:
[Table 1.] List of the parameters

List of the parameters
Functional leaf longevity (
The product of functional leaf longevity (
By substituting Eq. 3 and Eq. 4 into Eq. 2, GPP can be rewritten as:
The product of
>
Measurement of photosynthesis
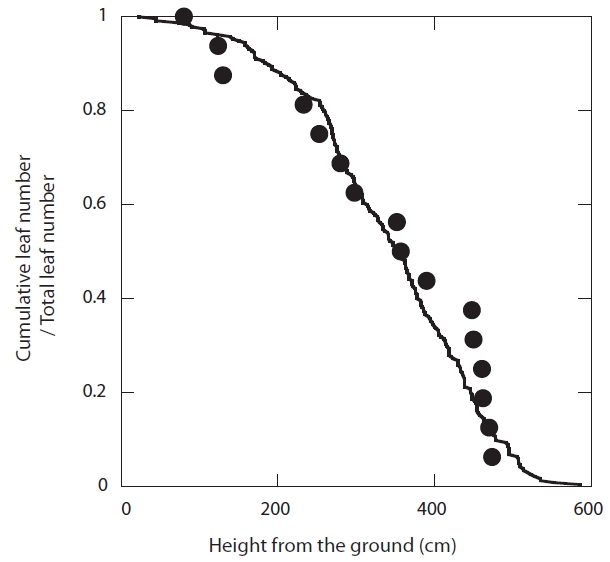
In 2007, a scaffolding tower that reached the canopy was constructed. A total of 16 leaves were selected from four trees from the entire position of the canopy (0.8-4.7 m from the ground). Sample leaves were selected from different heights, so as to represent the entire leaf population (Fig. 1). Photosynthesis measurements were repeated for the same leaves 6-13 times, from May to November of 2007. The number of measurements was smaller for the leaves that fell earlier. The photosynthetic rate of each leaf was measured using a portable infrared gas analyzer (LI-6400; LI-COR, Lincoln, NE, USA). Photosynthetic photon flux density (PPFD) 1,500 μmol m-2 s-1 was supplied until the equilibration of the leaf with an LED light source (LI-6400-02B; LI-COR) within the chamber. The equilibration required 10-20 minutes for the upper-canopy leaves, and 20-30 minutes for the lower-canopy leaves. CO2 concentrations inside the chamber were controlled at 350 ppm. We did not control the air temperature inside the chamber, which ranged from 22-30℃. Measurements were conducted from 8 to 11 a.m. each day. After each measurement, PPFD was changed to zero, and after equilibration (10-20 minutes), the dark respiration rate was measured. The gross light-saturated photosynthetic rate of the leaves on each day is acquired as the sum of the light-saturated net photosynthetic rate and the dark respiration rate.
For each of the monitored leaves, we sampled three adjacent leaves on the same horizontal branch in the summer. The areas of those leaves were determined via the analysis of digitally-scanned images with Adobe Photoshop Elements (Adobe Systems Inc., San Jose, CA, USA). The leaf samples were then oven-dried at 70℃ to a constant weight and weighed. The mean leaf mass per area of each of those three leaves was used as surrogate values for each of the monitored leaves. Using them, area-based photosynthetic- and respiration rates for each leaf were converted into mass-based values. Those leaf masses and the leaf litter were converted as follows: 1 g dry leaf = 0.5 g C (Yamasaki and Kikuzawa 2003), in order to obtain the carbon-based values.
Sample leaves for the photosynthesis measurements were monitored from leaf emergence until fall at 7-23-day intervals in 2007. Functional leaf longevity (
>
Data analysis for photosynthesis
The lifetime maximum instantaneous light-saturated net photosynthetic rate is used as the
The results were summarized in Table 2.
[Table 2.] The estimated parameters in 2007
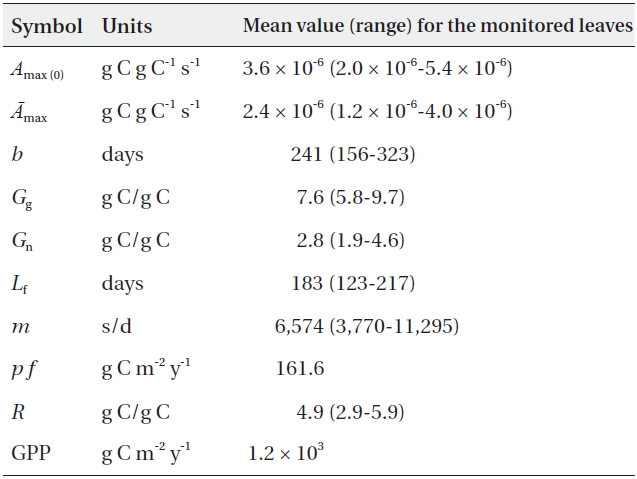
The estimated parameters in 2007
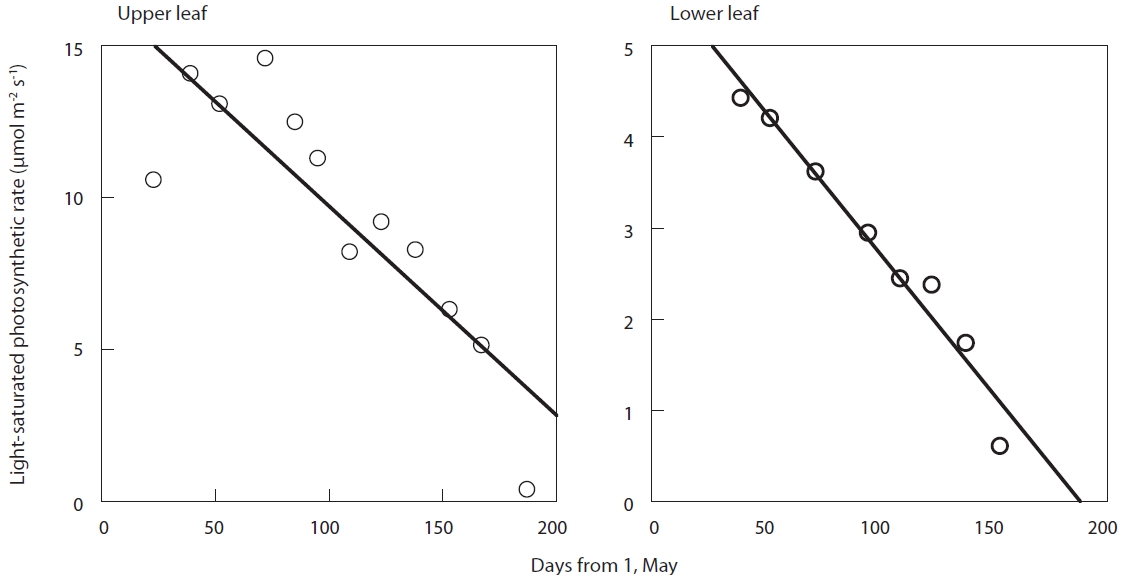
The light-saturated net photosynthetic rate of each leaf reduced in an almost linear fashion after full expansion (Fig. 2). The slope of the linear regression of light-saturated photosynthetic rate with time was found to be significant for all the leaves (
The estimated GPP of the forest (1.2 × 103 g C m-2 y-1) was within the GPP range of beech forests in central Japan (0.57 × 103-1.56 × 103 g C m-2 y-1, assuming that 1 g dry matter = 0.44 g C) previously reported by Kakubari (1991), which employs the conventional allometric method. This was also similar to the GPP range for a 30-year old European beech forest (1,000-1,300 g C m-2 y-1), which was estimated via eddy flux measurements (Granier et al. 2000). To the best of our knowledge, this is the first application of the leaf lifespan theory to the calculation of GPP. Although our method may be less accurate than the present eddy flux measurements, our theoretical approach produced a value proximate to the actual one.
The principal assumption of this model is that leaf longevity is determined so as to maximize whole-plant carbon gains in concert with the numerical model developed by Kikuzawa (1991). Many previous reports conducted in the tropics have corroborated the carbon-economy model (e.g. Reich et al. 1991, 1999, 2004, Vincent 2006). However, leaf longevity should be susceptible to the effects of strong seasonality in temperate regions (Reich et al. 2004, Vincent 2006, Koyama and Kikuzawa 2008). Nonetheless, two lines of evidence appear to suggest that leaf longevity in temperate regions functions as an indicator of the carbon budget of a plant. Firstly, temperate species were included in the worldwide leaf economic spectrum (Reich et al. 1997, 1999, Ackerly and Reich 1999, Wright et al. 2004, He et al. 2009). If the effect of seasonality is predominant, species in the temperate region should be outliers within those spectra; however, this is not the case. Secondly, variations in leaf longevity in temperate regions have also been predicted by carbon economy models (Hikosaka 2005, Oikawa et al. 2006, 2008). Even within the same temperate forest, deciduous and evergreen leaf habits coexist in microclimates, with deciduous trees tending to be found in more productive environments (Monk 1966, Chabot and Hicks 1982, Kikuzawa 1984, Koyama and Kikuzawa 2008). Leaf longevity in temperate regions should, assumedly, reflect the carbon economy of plants. Hence, the method presented herein should be globally applicable, based on the generality of the leaf economic spectra.