Satellite images are used for many applications such as reconnaissance and geographic information systems. Therefore, design and operation requirements of satellite systems have become more severe, and greater system reliability during operation is required. Satellite attitude control systems, including sensors and actuators, are critical subsystems, and any fault can result in serious problems. Therefore, various attitude estimation algorithms using multiple sensors are being actively studied for potential applications in satellite fault-tolerant systems (Ali et al., 2005; Edelmayer et al., 2007; Karlgaard et al., 2008; Kerr, 1987; Xu, 2009).

Satellites use various attitude sensors including gyroscopes, sun sensors, star sensors, and magnetometers. There are several satellite attitude estimation algorithms including Kalman filter, extended Kalman filter (EKF), unscented Kalman filter (UKF), and particle filters (Crassidis et al., 2007). EKF has been widely used to estimate the states of satellite systems. However, the nonlinearities of a satellite system are approximated by first-order Taylor series expansions that can provide poor estimates when the system has severe nonlinearities (Karlgaard et al., 2008). Recently, studies on UKF have been performed to capture the posterior mean and covariance to the third order. It is now known that the UKF can provide better results than the EKF (Ali et al., 2005).

For a multi-sensor system, there are two different filter schemes for the measured sensor data process: the centralized Kalman filter (CKF) and the decentralized Kalman filter (DKF) (Kim et al., 2003). In the CKF, all measured sensor data are processed at the center site, and therefore information loss can be minimized. However, this approach causes severe computational problems when the filter is overloaded with data, and the CKF could provide unreliable results. In the DKF, the local estimators of each sensor can generate global optimal or suboptimal state estimates according to the data fusion criterion. This scheme has advantages in the sense that (i) much more data can be treated because of the parallel structure, and (ii) a fault can be easily detected and isolated due to the decentralized scheme.

In this study, a decentralized Kalman filter scheme in federated configuration was adopted for satellite attitude estimation. A federated UKF can be effectively employed to detect and isolate a sensor fault (Ali et al., 2005; Edelmayer et al., 2007). Using a fault detection and isolation (FDI) algorithm, accurate attitude information can be provided despite the sensor fault, and therefore the satellite can perform its mission continuously. Generally, two FDI algorithms are used to detect and identify faults: (i) monitoring the measurement residual, and (ii) using a sensitivity factor (Ilyas et al., 2008). We used a sensitivity factor to detect and identify sensor faults. To verify the performance of the proposed algorithm, numerical simulations were performed for a satellite with a gyroscope and a star tracker as the attitude sensor. The numerical simulation shows that the proposed federated UKF with FDI algorithm detected and isolated the sensor faults effectively, and therefore provided accurate and robust attitude estimation results when the attitude sensor had a fault.

This paper is organized as follows. In Section 2, attitude kinematics and sensor modeling are described. The attitude estimation algorithms using UKF and federated UKF, and the FDI algorithm, are derived in Section 3. Numerical simulation and analysis to verify the proposed algorithm are shown in Section 4. Finally, conclusions are presented in Section 5.

In this study, a quaternion was used to describe the attitude dynamics of a satellite. A primary advantage of the quaternion is redundancy and a nonsingular attitude description (Schaub et al., 2003). The quaternion is a fourdimensional vector defined as

where

where e^{^} is the unit Euler axis and (특수문자) is the rotation angle. The quaternion satisfies the constraint q^T q=q₁²+q₂²+q₃²+q₄² = 1. The direction cosine matrix can be written in terms of the quaternion as

where I_3×3 is a 3×3 identity matrix and

Also, is the cross-product matrix defined by

The kinematic differential equation for the quaternion is given by

where ω is the three-dimensional (3-D) angular rate vector, and

The composition of the quaternion is defined by

The inverse quaternion is defined by

Note that q (특수문자) q^?1 = [0 0 0 1]^T, which is defined as the identity quaternion.

A gyroscope is a general sensor that measures the angular velocity of a satellite. The gyroscope system can be expressed mathematically by Frarrenkopf's model (Karlgaard et al., 2008). In this model, angular velocity is represented as the true angular velocity with an additive bias and Gaussian white-noise. The bias dynamics are considered to be driven by a Gaussian white-noise process. Also, in this model, it is assumed that the bias term can be regarded as the net effect of several systematic error sources such as scale factor errors, non-orthogonality, and misalignment. The gyroscope model is represented as

where ω is the measured angular velocity, ω is the true angular velocity, β is the drift, and η_v and η_u are independent zero-mean Gaussian white-noise processes with

where E[ ] denotes expectation and δ(t-τ) is the Dirac delta function.

It is known that the rate information from gyroscope measurements should be integrated to estimate the satellite attitude, and this measurement causes the estimates to drift from the true value. For this reason, it is necessary to use additional sensors, such as a star tracker, for drift error compensation. A star tracker is an optical device in an attitude control system that has the capability to recognize a star pattern and provide the attitude of a spacecraft (Jayaraman et al., 2006). The output of a star tracker is an estimated quaternion that relates the orientation of the body to the inertial frame. Quaternion estimates are assumed to be unbiased, but they have added random measurement noise. A star tracker model can be represented as (Karlgaard et al., 2008)

where q_s is a star tracker output vector that is a continuously measured quaternion vector, q is the quaternion representing the true orientation, and δ q_s is an independent zero-mean Gaussian white-noise process of the measurement noise quaternion vector with

For an n-state nonlinear system, the UKF algorithm can be summarized as follows (Simon, 2006):

where x_k is the state vector, y_k is the observation vector, w_k is the state noise process vector, and v_k is the measurement noise vector. It is assumed that the noise vectors are uncorrelated white Gaussian processes. The UKF was initialized as follows:

First, a time update was performed to propagate the state estimate and covariance from one measurement time to the next. To propagate from time step (k-1) to k, a set of sigma points was chosen using the current best guesses of the mean and covariance as follows:

For the state propagation step, the a priori state x^{^}_k^- and error covariance P_k^? were estimated using the propagated sigma point vectors as follows:

Thus, the measurement update was performed and is briefly summarized as follows. First, we selected the sigma points with appropriate changes using the current best guess of the mean and covariance. Thus,

The predicted observation vector y^{^}_k and its predicted measurement and cross-covariance between x^{^}_k^- and y_k were obtained as

Finally, the measurement update of the state estimate was performed using the normal Kalman filter equations as follows:

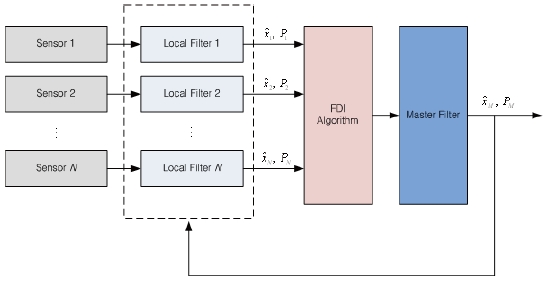
Federated filtering consists of two parts: local filters and the master filter. The local filters are parallel processed and independent of each other, and their estimated results are fused in the master filter. In each local filter, a local estimate is obtained using the measurements of local sensors. The master filter uses the estimates of the local filters to update the global state estimate in a fusion process, and this result is used for the initialization of local filters. This scheme has several features, one of which is the capability of fault detection and isolation of the local sensor during the process. The master filter is not affected by a local sensor failure (Ali et al., 2005; Edelmayer et al., 2007). The structure of the federated filter is shown in Fig. 1, and the filtering algorithm in each local filter is a UKF, as described in the previous section.

The master filter is processed at the same rate as the local filter. If all local estimates are uncorrelated, the global estimate from the master filter is given by

where x^{^}_i and P_i are the local estimate and the covariance of the i-th local filter, and P_M^-1 is called the information matrix. Note that the global estimate is the sum of the local estimates and a linear-weighted combination with weighting matrices P_i^{-1(i=1,2,...,N)} and P_M^-1.

A federated UKF can provide accurate and robust state estimation values without interrupting the mission because the FDI algorithm is employed in a fault-tolerant configuration. Fault detection usually requires continuous careful monitoring of the measured output data. In a normal case, the output data follow known patterns of evolution with limited random disturbance and measurement noise. However, the measured output data change their nominal evolution pattern when sensor failures occur. General fault detection algorithms are based on considering these differences between the evolution patterns and the measured output data (Ilyas et al., 2008). In this study, the sensitivity factor was used for the FDI as follows:

When S_i is smaller than a threshold value, then the i-th sensor is considered to be working well, x^{^}_M and therefore its output can be used to calculate the global estimates and P_M. However, if S_i is larger than a threshold value, then the i-th sensor could be having some problems. In this case, global estimates should be obtained without using the output of the i-th sensor. The threshold value can be selected based on a Chi-square distribution and optimized in the experiment for the particular application.

In this section, we describe numerical simulations used to verify the performance of the proposed attitude estimation algorithm based on the federated UKF. For the satellite attitude estimation, two types of attitude sensors were used: a gyroscope and a star tracker. The integrated system can provide accurate estimates for a satellite system with sensor uncertainties such as sensor drift, scale factor errors, and shutting off the power. Two simulation cases were considered: (i) no sensor fault, and (ii) a star tracker with a fault.

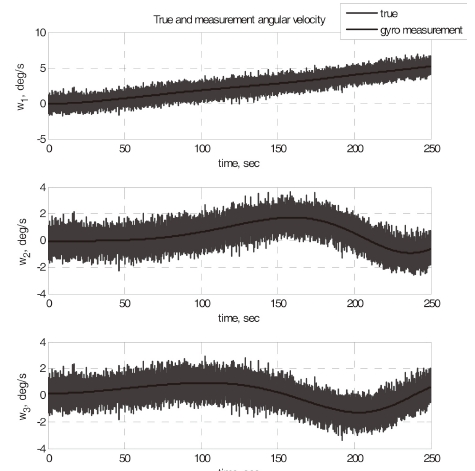
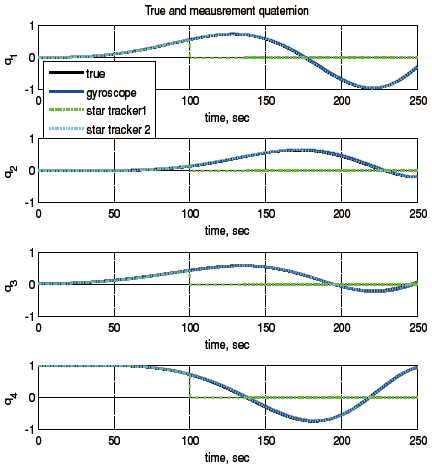
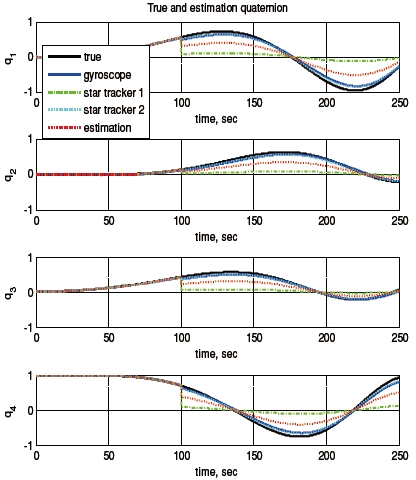
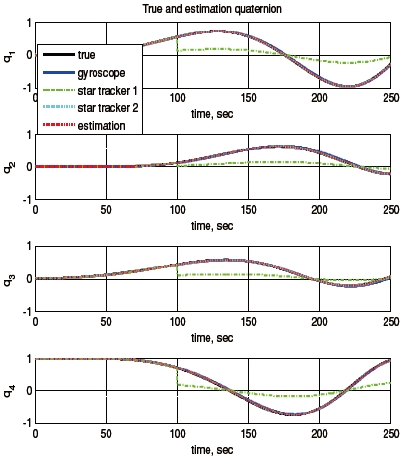
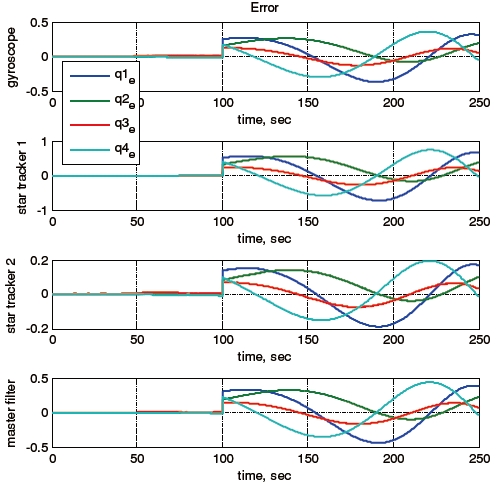
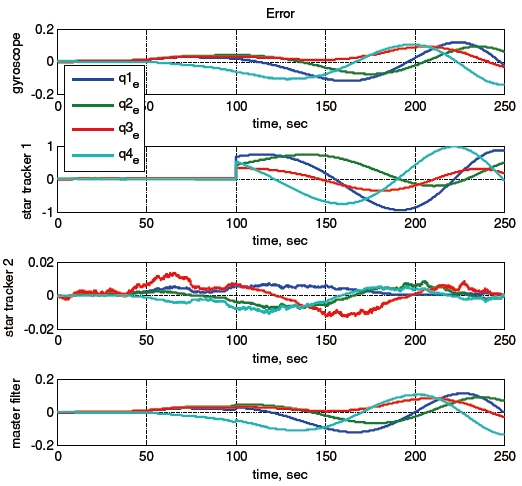
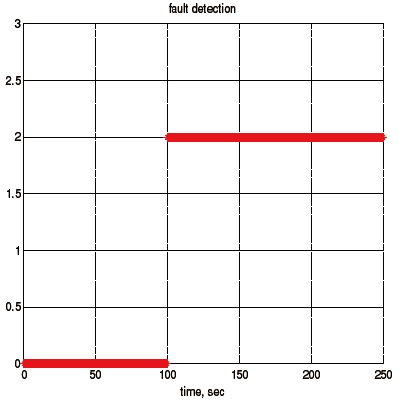
Consider a sensor failure of star tracker A. Figure 2 shows the measured angular velocity history, and Fig. 3 shows the quaternion history when star tracker A has a problem at 100 seconds. Figures 4 and 5 illustrate the local estimates and global estimate without and with the FDI algorithm, respectively. Figures 6 and 7 show the attitude error histories without and with FDI algorithm, respectively, and Fig. 8 shows the fault detection using the FDI algorithm. In this simulation, the fault detection logic was modeled as summarized in Table 1.

The results show that the errors of the global estimate without the FDI algorithm increased after the occurrence of the star tracker failure. This is because the global estimate was calculated using not only healthy sensor measurements, but also the faulty measurement. However, even though one of the star trackers had a fault, the errors of the global estimate remained small when the FDI algorithm was used. Figure 8 also shows that the star tracker failure was detected and isolated immediately after the sensor failure occurred at 100 seconds, which led to many smaller errors of the global estimate compared to the results without the FDI algorithm.

Table 2 summarizes the performance of the proposed algorithm. As shown in Table 2, the performance of the federated UKF with FDI algorithm significantly improved in case 2. We note that the total error of the global estimate using the federated UKF with the FDI algorithm was much smaller than the result without the FDI algorithm. Thus, we conclude that the proposed federated UKF with the FDI algorithm provided an accurate and robust global estimate for satellite attitude estimation even though the attitude sensor had a fault.

In this study, a federated UKF with an FDI algorithm was proposed for satellite attitude determination. The UKF gives accurate estimates for nonlinear systems, and the federated UKF makes the system robust and stable. Since the FDI algorithm can help to detect and isolate sensor failure immediately, the global estimate is not affected by a faulty local estimate. Therefore, the error of the global estimate using the federated UKF and FDI algorithm is smaller than that using only the federated UKF. Numerical simulation results show that the proposed algorithm has efficient and accurate performance for satellite attitude determination when attitude sensors have a fault. The proposed algorithm can be applied to satellite systems, ground mobile robots, and aerial robot systems.