As the digital information network develops rapidly, there has been strong need for information security because personal information is in danger of leakage due to the lack of security provisions. However, most cryptosystems using electronic digital processing have a problem of information cracking. For the purpose of solving this problem, various kinds of optical encryption systems more complicated and rigid against information cracking than electronic digital encryption have been proposed recently.[1-6] In each case the optically encrypted information has complex values, and thus holographic recording may be required. This requirement makes it difficult to store and transmit the encrypted information over a digital network. However, optical encryption and decryption to record and reconstruct the complex values can be easily performed using a phaseshifting digital holographic technique. A phase-shifting digital holographic technique that uses a charge-coupled device(CCD) camera for direct recording of a hologram has an advantage of real time digital information processing without using holographic recording media, and can record the full complex information.[7-18] Phase-shifting digital holography to reconstruct the amplitude and the phase of light is more accurate than off-axis holographic techniques which record digital holograms. The optical encryption and decryption with this phase-shifting digital holographic technique has been well achieved for binary bit data, but is not good for a gray-level optical image. Recently, we proposed an optical encryption of gray-level image using on-axis and 2-f digital holography with 2-step phase-shifting method, in which a gray-level image is changed into binary data by ASCII encoding.[14]

In this paper, we propose a technique for an opticalcryptosystem of 256 gray-level optical image by using aquadrature phase shift keying(QPSK) digital modulationmethod and 2-step phase-shifting digital holography. Thebasic idea is that we are able to calculate the QPSKmodulated phase values from two encrypted digital holograms.A gray-level optical image is digitized into 8-bits binary

data by ASCII encoding. The 8-bits binary code correspondingto one gray-level value is expressed by four pairof quadrature phase values in a block having 2×2 pixelsby QPSK modulation. The converted QPSK phase valuesand a security key code are displayed on a phase-typeSLM(Spatial Light Modulator). The encrypted digital hologramsare obtained by interference between an object beamwhich has the QPSK modulated phase codes and areference beam which has the security key code, and then256 gray-level quantized digital holograms are acquired bythe CCD. These encrypted digital holograms can be storedby computer and transmitted over a digital network. TheQPSK phase values are reconstructed from the encodeddigital holograms by the same security key, and theoriginal gray-level optical image is decrypted by ASCIIdecoding. In section 2, the optical encryption system ofthe gray-level optical image using QPSK modulation and2-step phase-shifting digital holography is described. Insection 3, we describe computer simulations and results ofthe encryption and decryption. Finally, conclusions arebriefly summarized in section 4.

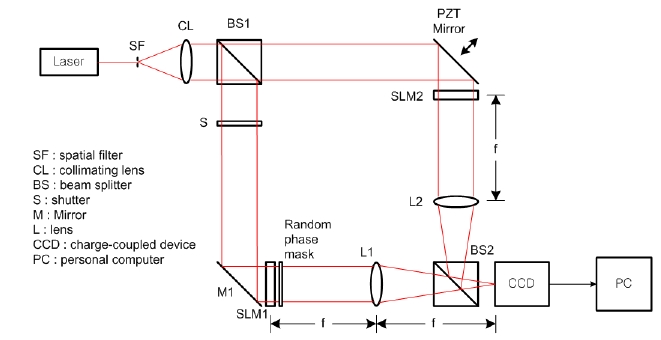
Fig. 1 shows the optical setup for encryption with phaseshifting digital holography, which is based on Mach-Zehnder type interferometer architecture. Beam splitter BS1 divides collimated light into two plane waves, the reference and the object beams. With shutter S open and after reflecting in a mirror M1, the object beam illuminates the phase-type SLM(SLM1) which then displays QPSK phases to be encrypted. The output beam from SLM1 is multiplied by a random phase mask, resulting in Fourier transform on CCD by lens L1. The random phase mask widens the dynamic range of the Fourier transform in the spatial frequency domain. The reference beam after being reflected by PZT mirror illuminates the phase-type SLM(SLM 2), where another random phase pattern with a security keycode information is displayed, and is Fourier transformedon CCD by lens L2. This concept is analogous to a doublerandomphase encoding method.[4] However, since theproposed encryption system uses phase masks at thespatial plane instead of placing the phase mask at thespatial frequency plane, it has advantages of requiring lessprecise alignment and a simpler setup. Also, the codeinformation of the random phase mask pattern used in theobject beam can be used simultaneously as the samerandom phase pattern of the security key code in thereference beam when making a digital interference hologram.But if we use a new random phase pattern of the securitykey code different from the random phase mask pattern inthe object beam, the proposed cryptosystem has a higherlevel of security with two security keys and is morecomplicated.

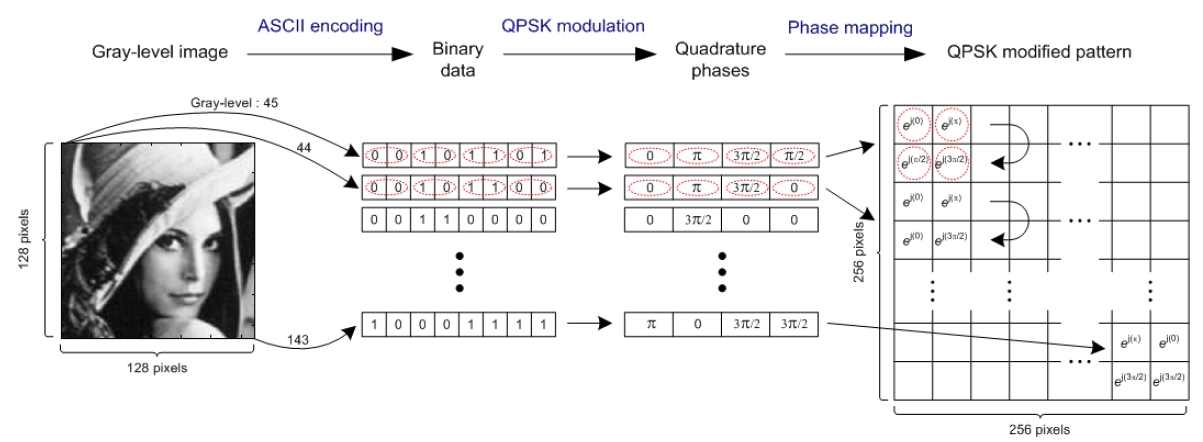
Let f(x, y) be a gray-level optical image function to be encrypted. The 256 gray-level optical image is digitized into 8-bits binary bit data by ASCII encoding method. This 8-bits binary code corresponding to one gray-level value is converted into four pairs of quadrature phase values in a block having 2×2 pixels by binding each two bits from MSB(most significant bit) of 8-bits data and modulating it to QPSK phase values. Fig. 2 shows the converting procedure.

Put s(x, y) be quadrature phase function after encoding f(x, y) into ASCII codes and QPSK digital modulation. In order to display QPSK phase values on the phase-type SLM1, this QPSK phase function have to be represented as

where x and y are transversal coordinates at the spatialplane.

Let k(x, y) with individual values equal to 0 or 1, be a binary bit code that can represent a security key. This security key is changed to a binary phase angle θ(x, y)=π {1-k(x, y)}, which is converted again into a phase pattern function b(x, y) in order to be displayed on the phase-type SLM2.

If the binary bit code is random, b(x, y) is also randomphase pattern. The multiplication of the QPSK phasefunction with the security key phase pattern function isrepresented as

Fourier transform of o(x, y) is expressed as

where α and β are transversal coordinates at the spatialfrequency plane.

The random phase pattern with unit amplitude can bedisplayed on the phase-type SLM2 and is expressed as

where unit amplitude is implemented optically by a plane wave in the reference beam. The Fourier transform of r(x, y) is expressed as

The digital holographic intensity pattern recorded byCCD camera at the spatial frequency plane is given by

with the reference beam and the object beam given by Eqs. (4) and (6), where Δφ = φ_O-φ_R is the phase difference between the object and the reference beams. The precise phase information can not be acquired by intensity information of Eq. (7) alone. In this paper, we use the phase-shifting digital holography. This technique provides the exact reconstruction of the phase difference between the object and the reference beams and amplitudes of these two beams. Two intensity patterns in the form of a digital hologram are achieved by 2-step phase-shifting holography with the reference beam phase shifted by φ_i = 0 and π/2 for i =1, 2, respectively. The phase shift with phase step of π/2 is obtained by properly moving the PZT controlled mirror. Another phase shifting technique, instead of moving the mirror, is to use a phase-type SLM, which is electronically controlled to allow phase shift π/2 in the reference beam. By rewriting Eq. (7), the phase-shifting digital hologram is expressed as

This 2-step phase-shifting digital holography has themerit of a reduced number of holograms compared tomulti-step phase-shifting holography. From Eq. (8), 2-stepphase-shifting digital holograms are obtained by

These two digital holograms are encrypted data, whichare stored in a computer and transmitted through thedigital communication network.

After receiving the digital holograms and manipulating them, the exact retrieval of the original gray-level optical image has to be done with the same security key. With Eq. (9), let 'O(α, β)'²+'R(α, β)'² meaning the DC-term is A(α, β ) and

meaning the AC-term is B(α, β ), then Eq. (9) is rewritten by

After the DC-term A(α, β ) is removed in Eq. (10), modified holographic intensities are expressed as

From Eq. (11), the phase difference of the object beamand reference beam is calculated as follows.

The DC-term removal is effective for calculating the phasedifference easily. Using Eqs. (12) and (13), the magnitudeof the AC-term is calculated as follows.

From Eqs. (13) and (14), the complex hologram withencryption information is expressed as

In order to get the complex distribution O(α, β ) and decrypt the original 256 gray-level image, we need the complex distribution R(α, β ) of the key code phase pattern. Note that it is possible to get R(α, β ) with knowledge of the phase pattern because the phase pattern is made by the known binary key code. To reconstruct O(α, β ), we also need the intensity distribution 'R(α, β )' of the key code phase pattern. The intensity pattern recorded by the CCD camera gives 'R(α, β )' ² by removing the object beam inMach-Zehnder interferometer shown in fig. 1, which isdone by closing shutter S. Using the complex hologramand the security key code information, the reconstructedcomplex distribution is obtained by

By using an inverse Fourier transformation, the information of the object beam is reconstructed and the reconstructed data represents the function o(x, y), which is the multiplication of the original QPSK phase function and the original security key phase pattern function.

This reconstructed information expressed as Eq. (17) isprocessed again using the same security key for the purposeof acquiring the original QPSK modulated phasefunction as follows.

where ^* means complex conjugate. Therefore, the original 256 gray-level optical image of f(x, y) can be decrypted by ASCII decoding from Eq. (18).

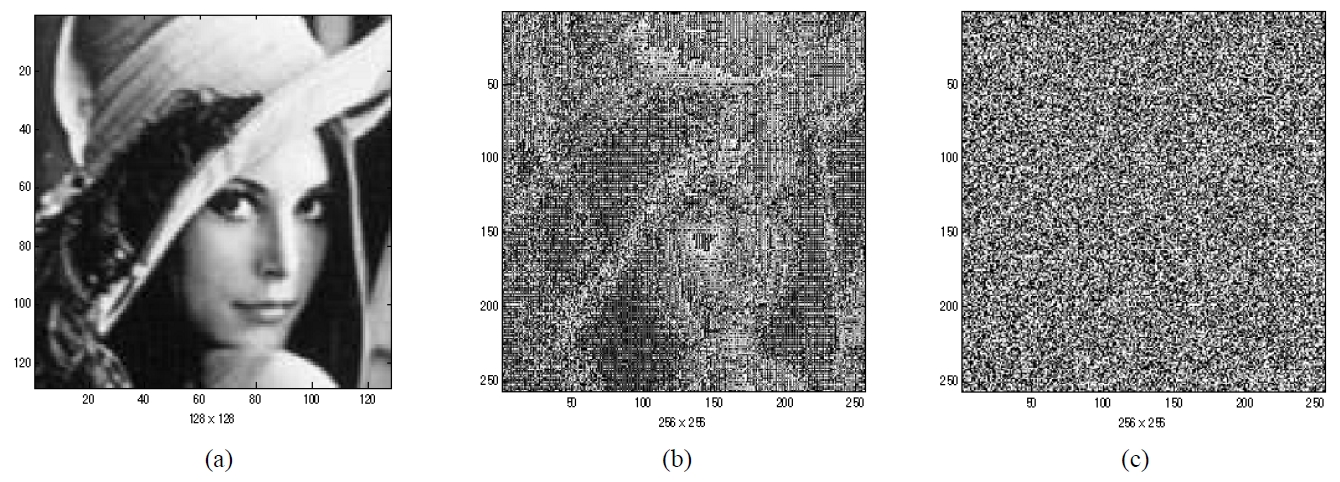
We show the performance of the proposed cryptosystem by using computer simulations. The Lena image 128×128 pixels in size with 256 gray levels shown in Fig. 3 (a) is used as the optical image to be encrypted. Fig. 3 (b) represents the converted phase values of the QPSK modulated function. We use an ASCII encoding technique for changing the 256 gray-level Lena image into binary bit data. The 8-bits binary data corresponding to one gray-level value is mapped to four pairs of quadrature phase values and is arranged in a block having 2×2 pixels in a clockwise sequence by QPSK modulation, and the converted data expands to 256×256 pixels in size. Fig. 2 shows the proposed encoding and QPSK digital modulation technique. Fig. 3 (c) shows a random generated security key code for encryption and decryption and has also 256×256 pixels in

size, where white areas have value of 1 and black area is0 numerically. The security key code pattern was generatedfrom a random generator in MATLAB Program.

Fig. 4 shows two encrypted digital holograms using phase-shifting digital holography. Each hologram is quantized with 256 gray levels. From the complex hologram calculated by the encrypted phase and amplitude, reconstruction and decryption of the encrypted phase information are carried out successfully by the same encrypting security key.

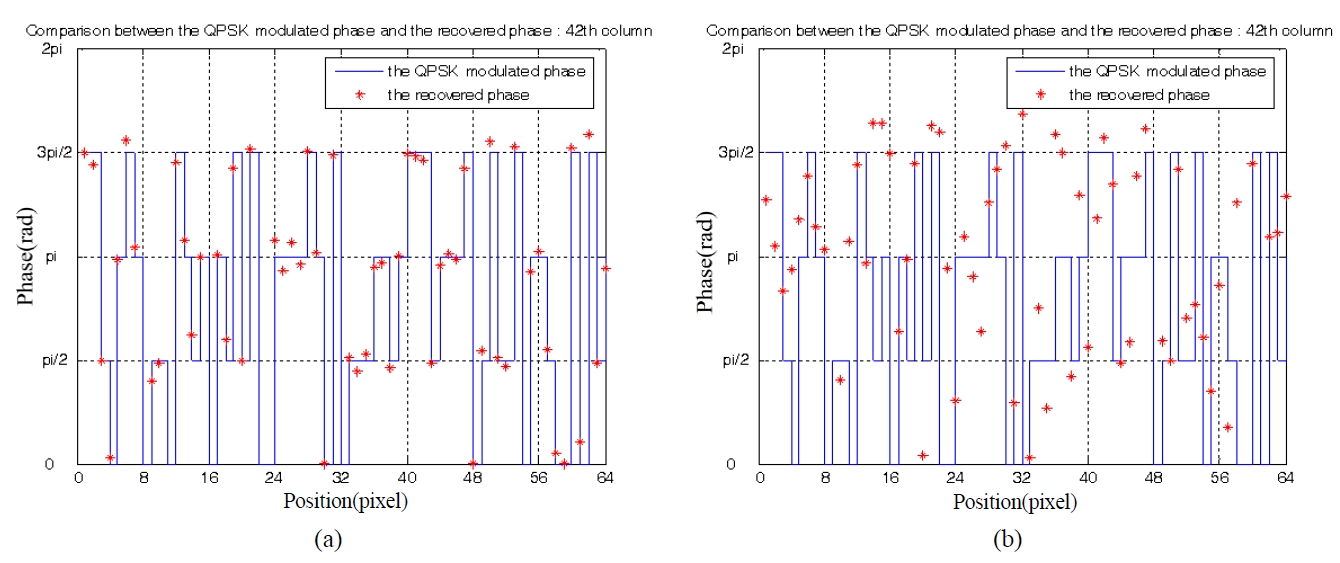
Fig. 5 shows the phase difference between the encrypted phases generated from a gray-level image by QPSK digital modulation and the recovered phase values by the proposed cryptosystem. Fig. 5 (a) shows an approximate value of the recovered phase when the correct security key is used, and the exact original quadrature phase value can be reconstructed from the recovered phase value by proper estimation and decision method. Fig. 5 (b) shows an approximate value of the recovered phase when the incorrect security key is used, and some recovered phases are far from the original quadrature phase values.

Fig. 6 shows results of reconstruction and decryption. Fig. 6 (a) is the reconstructed phase values of the image when the correct security key is used, where the exact original quadrature phase values can be obtained from the recovered phase values by proper estimation and decision algorithms. We notice DC-term removal is essential to reconstruct the original phase data for 2-step phase-shifting digital holography. If the incorrect key is used for reconstruction, the original phase values will not be

reconstructed and these phase data will not be decodedinto the original Lena image.

IV. CONCLUSION

We propose a new optical cryptosystem of gray-level optical image using QPSK digital modulation method and digital holographic technique with 2-step phase-shifting method. A gray-level optical image is digitized into 8-bits binary bit data by ASCII encoding method and these binary bit data are expressed by four pairs of quadrature phase values in a block having 2×2 pixels by QPSK digital modulation. After ASCII encoding and QPSK modulation, the size of data to be encrypted expands to two times more than the original size of the gray-level optical image. The modified information data with corresponding phase values is displayed on a phase-type spatial light modulator and is encrypted with a security key by using optical digital holography. The security key is expressed with random binary phase. Two-step phase-shifting is implemented by controlling the PZT mirror with phase steps of 0 or π/2. The proposed system is based on Mach-Zehnder type phaseshifting digital holography, which has advantages of compactness, easy configuration of the optical system, and security improvement. The digital hologram in this method is a Fourier transform hologram and is recorded on a CCD camera with 256 gray-level quantized intensities. For encryption, we use a random phase pattern to enlarge the dynamic range of the Fourier transform hologram in the spatial frequency plane. The random phase that is masking the QPSK modulated phase data with image information and the random phase pattern displayed on the phase-type SLM with the security key code are statistically independent. DC-term removal of the phase-shift digital hologram is performed, which is essential to reconstruct the original phase data in 2-step phase-shifting digital holography. The method using 2-step phase-shifting digital holography is more efficient than the multi-step phase-shifting method because 2-step phase-shifting method produces less data to be transmitted than the multi-step method does. The simulation result demonstrates that the proposed technique is good for encryption and decryption of gray-level optical images and can be used for cryptosystems and security applications systems.