Feedback control systems consist of plants to be controlled and controllers stabilizing closed loop systems. The plants generally are described by mathematical models, which are called the nominal models without plant uncertainty. The plant uncertainty results from mathematical error between the nominal models and real models or corrupted feedback signals. Therefore, in real world, the plant uncertainty should be considered and if a controller in the presence of the plant uncertainty stabilizes a closed loop system and meets design specifications of the closed loop systems then the controller is called a robust controller. Thus, the robust controller should meet robust stability and robust performance. In our previous work, P2/LTR was proposed to satisfy time domain design specifications. However, because the proposed method was only for a nominal plant, the robustness was not considered. In this paper, robust control is proposed to meet both robust stability and robust performance in the presence of plant uncertainty. The plant uncertainty is mathematically designed so as to carefully describe the model uncertainty, and as for the model uncertainty plant input multiplicative uncertainty is used. Firstly, a nominal model is designed for nominal control, secondly a model with uncertainty and a performance bound are designed, and finally a robust controller is designed to satisfy both robust stability and robust performance. In this paper, it was verified that a parameter ρ determines robustness in P2/LTR framework.
수학적 공칭 모델 (nominal model)과 실제 모델과의 차이인 모델 불확실성 (model uncertainty)은 필연적이므로, 실제 제어 시스템은 이러한 불확실성이 존재하는 상황에서도 안정도와 성능이 보장되어야 한다. 그러므로 이를 각각 안정도 강인성(robust stability)와 성능 강인성 (robust performance)라고 정의하며 실제 제어 시스템에서 중요하게 고려되고 있는 하나의 성능 지표이다[1].
산업 현장에서 사용되고 있는 여러 제어 시스템 중에 모터 제어 시스템은 가장 널리 사용되고 있다[2,3]. 그러므로 모터는 전체 시스템의 핵심부품이고 그 모터의 움직임을 적절히 조절하는 것이 전체 시스템의 성능을 올리는 핵심 기술이다. 모터 움직임을 방해하는 요소 중 하나는 진동이며, 그 진동을 줄여주는 것이 전체 시스템 성능을 올릴 수 있는 중요한 하나의 방법이다. 진동은 크게 두 가지로 나뉘는데, 외부에서 들어오는 진동과 내부에서 발생하는 진동으로 구분된다. 일반적으로 외부에서 인가되는 진동은 전통적으로 외란 관측기(disturbance observer)를 이용하여 제거된다[4]. 이러한 전통적인 방법인 주파수 영역에서 설계하는 방법과 다르게 상태 공간에서 외란 관측기가 설계되는 방법이 제시되었다. 그중에서, 병렬 구조를 이용하여 기존의 상태변수를 이용할 수 있는 장점을 갖는 방법[5], 정상상태 (steady state)에서 현재 상태 추정기 (current state estimator)와 실제 플랜트 출력과의 차이를 등가 외란 (equivalent disturbance)으로 생각하고 그 외란을 제거하는 방식[6], 외란 제거기의 안정화를 위한 Q 필터를 최적화 방법으로 설계하여 준최적 외란 관측기를 설계하는 방법[7], 그리고, 최적 외란 관측기를 설계하는 방법[8] 등이 제안되었다.
모터 내부에서 인가되는 진동은 제어기 설계 당시에 감쇄비 (damping ratio)를 줄여서 내부에서 발생되는 진동 자체를 억제한다. 일반적인 방법 중 하나는 그 감쇄비를 충분히 반영한 극점 배치법[9]이 널리 사용된다. 그러나 극점 배치법은 모델 불확실성에 대한 안정도 강인성을 보장하지 못한다. 그러한 안정도 강인성을 보장하는 하나의 방법으로 LQG/LTR (linear quadratic gaussian / loop transfer recovery)이 제안되었다[10]. LQG/LTR은 오래전에 개발된 방법론이지만 현재까지도 사용되어, DC-AC 변환기[11]와 레이저 유도무기 시스템[12] 등에도 사용되고 있다. 그러나 일반적으로 LQG/LTR은 주파수 영역에서 설계 방법론이기 때문에, 시간 영역에서 진동 모드 억제를 위한 제동 제어 (damping control)를 할 수가 없었다. 이 문제점을 해결하기 위하여 최근에 P2/LTR (pole placement / loop transfer recovery)가 개발되어 LQG/LTR의 시간 영역에서의 설계 제약을 해결하였다[13].
이 논문은 기존의 연구를 확장하여 안정도 강인성뿐만 아니라 성능 강인성까지도 만족할 수 있는 강인 제어 방법을 제시한다. 여기서, 모델 불확실성을 수학적으로 명확하게 표현하기 위하여 플랜트 입력 곱셈형 불확실성 (plant input multiplicative uncertainty)을 추가하였고, 성능 강인성을 측정하기 위해 플랜트 출력 민감도 함수를 성능 영역(performance bound)를 정의한 후, 안정도 강인성과 성능 강인성을 모두 보인다.
논문의 구성은 다음과 같다. 제 2장에서는 공칭 모델의 대한 플랜트 모델링을 보이고, 제 3장에서는 불확실성 모델과 성능 영역을 설계한다. 제 4장에서는 강인 제어기 설계 방법을 보이며, 마지막 장에서는 결론을 기술한다.
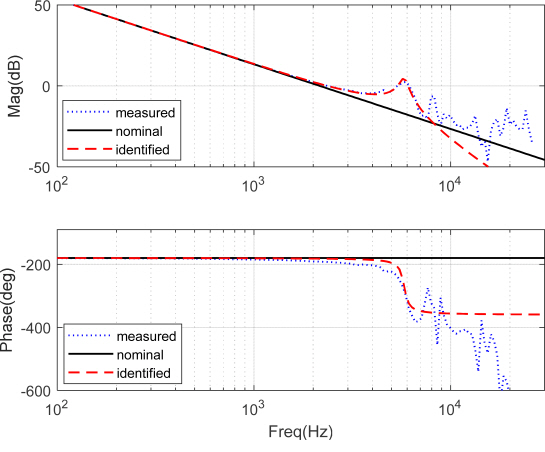
플랜트의 동적 특정은 동적 신호 측정기(dynamic signal analyzer)와 레이저 도플러 진동계(laser doppler vibrometer)를 이용하여 측정되고, 그 측정된 데이터로부터 수학적인 모델을 유도한다.
그리고 측정된 응답특성을 이용하여 다음과 같은 모델을 유도하였다.
여기서,
여기서,
이 장에서는 안정도 강인성을 위한 불확실성을 고려한 모델과 성능 강인성을 위한 성능 제한 영역을 설계한다.
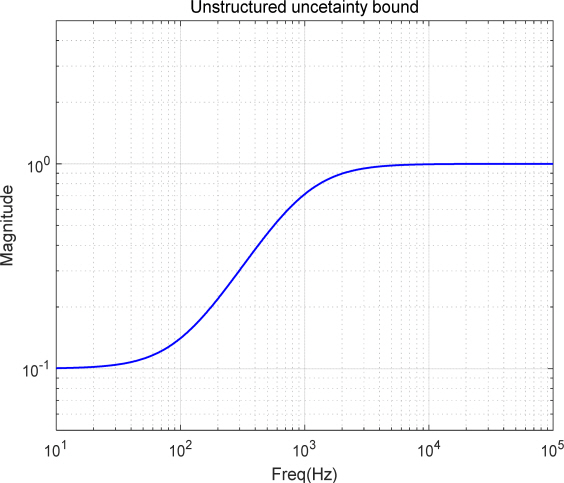
이제, 이 논문에서 주장하고자 하는 강인 제어를 위하여 플랜트의 불확실성을 모델링한다. 일반적으로 모델 불확실성은 저주파 영역에서는 작고 고주파 영역에서는 점차 커지며 이러한 특성이 잘 표현되도록 모델 불확실성을 추가한다. 모델 불확실성을 추가하는 방법은 여러 가지가 있는데, 플랜트 입력 곱셈형 (plant input multiplicative uncertainty), 플랜트 출력 곱셈형 (plant output multiplicative), 덧셈형 (additive uncertainty), 그리고 되먹임 (feedback uncertainty) 등이 있다. 이 논문에서는 플랜트의 불확실성을 명확하게 보여주는 곱셈형 불확실성을 사용하며 그중에서 플랜트 입력 곱셈형을 사용한다. 실제 SISO (single input single output) 시스템에서는 플랜트 입력 곱셈형을 사용하든 플랜트 출력 곱셈형을 사용하든 동일한 불확실 모델을 얻는다.
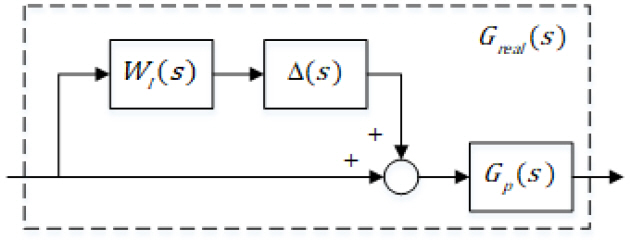
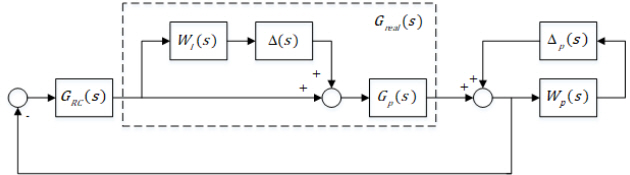
아래는 플랜트의 불확실성을 포함하는 실제 플랜트를 모델링한 것이다. 플랜트 혹은 모델의 불확실성은 크게 두 가지의 형태로 표현될 수 있는데, 하나는 파라미터 불확실성을 나타내는 구조적 불확실성 (structural uncertainty)와 주파수 영역에서의 불확실성을 하나의 큰 덩어리(lump)로 해석하는 비구조적 불확실성 (unstructural uncertainty)으로 나타내질 수 있다[1]. 또한, 비구조적 불확실성은 덧셈형 불확실성 (additive uncertainty), 입력 곱셈형 불확실성 (input multiplicative uncertainty), 출력 곱셈형 불확실성 (output multiplicative uncertainty), 입력 되먹임 불확실성 (input feedback uncertainty), 출력 되먹임 불확실성 (output feedback uncertainty) 등으로 표현된다. 이 논문에서는 <그림 2>와 같이 불확실성의 이득을 명확히 표현할 수 있는 입력 곱셈형 불확실성을 사용한다. 실제로, 단일 입력 단일 출력 (single input single output) 시스템에서는 입력 곱셈형 불확실성과 출력 곱셈형 불확실성은 수학적으로 동일하다[14].
그러므로, <그림 2>에서 불확실성이 포함된 실제 모델은 식 (3)와 같이 표현된다.
여기서,
위 모델 불확실성을 전달함수로 표현하면 다음과 같다.
여기서,
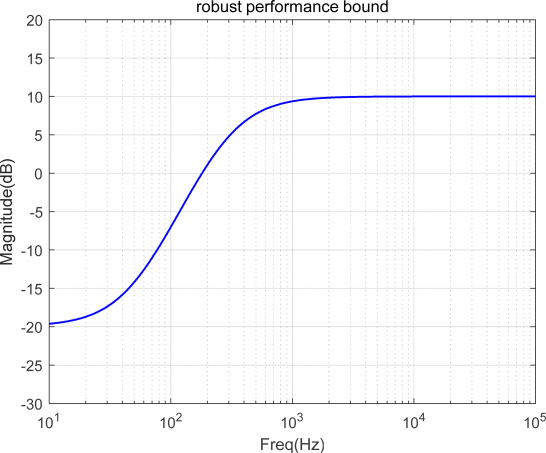
성능 지표는 여러 가지가 있으면, 그 중에서도 h 외란 감소 특성을 잘 표현한 민감도 (sensitivity) 함수의 특성이 대표적이다. 민감도 함수의 특성은 최대치 (peak)와 차단 주파수 (crossover frequency)로 표현되며, 이를 <그림 4>에 표현하였다.
그리고 이것을 수식으로 표현하면 식 (5)와 같다[1].
여기서
이 장에서 설계된 식 (4)와 (5)는 다음 장에서 안정도 강인성, 성능 강인성을 만족하는 제어기 설계에 사용된다.
이 장에서는 첫째 공칭 모델에 대한 제어기를 설계한 후, 두 번째 모델 불확실성이 존재할 때 강인 제어기를 설계한다. 그리고, 설계된 두 제어기를 비교하여 강인 제어기 설계 시 고려해야 할 점을 논한다.
공칭 모델에 대한 제어기 설계는 기존의 논문[13]에 나와 있으므로 여기서는 간략히 축약하여 서술한다.
제안하는 P2/LTR 방법에서는 목표 전달 함수를 먼저 설계한 후, 루프 전달 회복을 통하여 폐루프 시스템이 원하는 특성을 갖도록 한다. 이를 위하여 식 (6)과 같은 상태 추정기를 사용한다.
여기서
플랜트 입력에서 정의된 목표 전달함수
그리고 이 계수들을 만족하는 목표 폐루프 시스템의 극점
즉, 2차 시스템의 경우 우리가 원하는 시간 영역 응답특성을 갖는 폐루프 시스템은 식 (8)을 통하여 얻을 수 있고, 이를 우리가 얻고자 하는 목표 전달 함수로 설정하는 것이다. 식 (8)을 이용하여 얻는 목표 전달함수는 다음과 같다.
루프 전달회복을 위한 추정기 이득
여기서, Q= G 1 G 1 T =B B T 는 프로세스 잡음 공분산 행렬이고, R= ρ −1 G 2 G 2 T = ρ −1 은 측정 잡음 공분산 행렬이다. 상태 추정기 식 (6)으로부터 제어기 전달함수
이를 주파수 영역에서 변환하면 다음과 같다.
그리고, 개루프 전달함수는
정리하면, 공칭 모델에 대한 제어기 설계는, 우선 원하는 감쇠 계수
안정도 강인성과 성능 강인성을 동시에 만족하는 강인 제어기는 모델 불확실성이 존재하는 모든
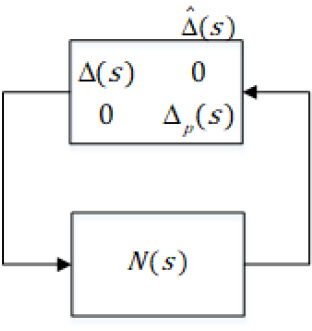
<그림 5>에서, ∆(
즉, Δ ^ (s) ∞ ≤1 이므로 아래와 같은 새로운 N Δ ^ 을 구성할 수 있으며,
식 (16)을 만족하는 제어기는 안정도 강인성과 성능 강인성 두 가지를 모두 만족한다 [1].
식 (16)을 전 주파수 영역에서 응답특성을 나타내기 위해선 μ Δ ^ (N) 의 구조화된 특이값(structured singular value)으로 나타내었다.
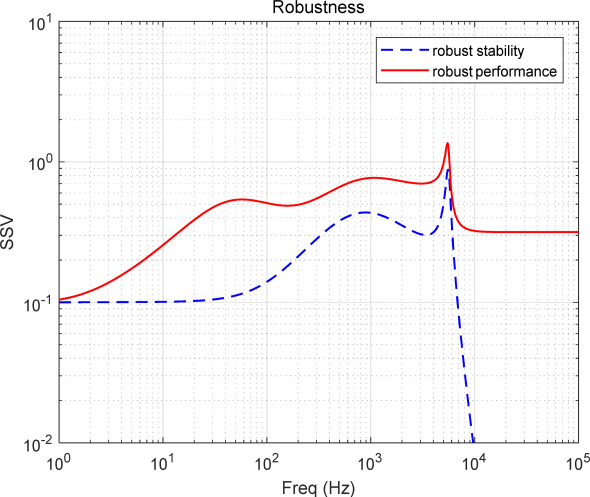
<그림 7>은 강인 제어기인
<그림 7>을 보면, 안정도 강인성은 모두 1보다 작기 때문에 공칭 모델에서 설계된 제어기
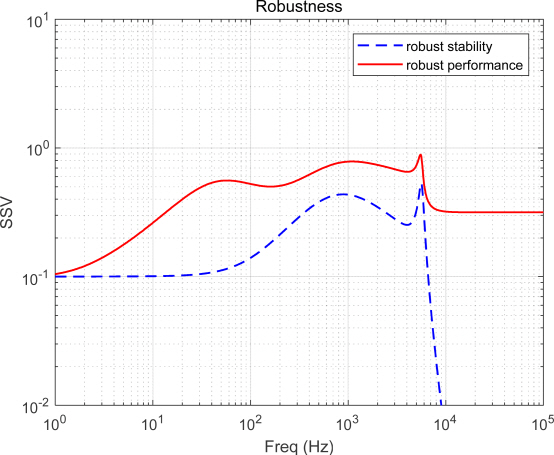
<그림 8>은
그러므로, 이 논문은 P2/LTR 구조에서 설계 파라미터인
기존에 제안하였던 P2/LTR 제어기를 확장하여, 강인 P2/LTR 제어기 설계 방법을 제안하였다. 강인 제어기의 충분 조건인 안정도 강인성과 성능 강인성을 보장하기 위한 프레임 워크를 보였고, P2/LTR 구조에서 두 가지 성능을 동시에 만족하는 설계 파라미터