Optical Design of an Image-space Telecentric Two-mirror System for Wide-field Line Imaging

Lee
Jong-Ung; Kim
Youngsoo; Kim
Seo Hyun; Kim
Yeonsoo; Kim
Hyunsook

doi:10.3807/COPP.2017.1.4.344

OA학술지
Current Optics and Photonics

Optical Design of an Image-space Telecentric Two-mirror System for Wide-field Line Imaging

DOI : 10.3807/COPP.2017.1.4.344
Author: Lee Jong-Ung, Kim Youngsoo, Kim Seo Hyun, Kim Yeonsoo, Kim Hyunsook
Publish: Current Optics and Photonics Volume 1, Issue4, p344~350, 25 Aug 2017

ABSTRACT

We present a new design approach and an example design for an image-space telecentric two-mirror system that has a fast f-number and a wide-field line image. The initial design of the telecentric mirror system is a conventional axially symmetric system, consisting of a flat primary mirror with fourth-order aspheric deformation and an oblate ellipsoidal secondary mirror to correct spherical aberration, coma, and field curvature. Even though in the optimized design the primary mirror is tilted, to avoid ray obstruction by the secondary mirror, the image-space telecentric two-mirror system shows quite good imaging performance, for a line imager.

KEYWORD

Two-mirror system , Image-space telecentricity , Flat field aplanat , Wide field mirror system , Hyperspectral imaging

본문

Collapse all

I. INTRODUCTION

The most useful characteristic of a mirror system is that the system does not have any chromatic variation. In the conventional axially symmetric configuration, a mirror system has a central obstruction and field-of-view restriction due to the vignetting effect. Hence, such a mirror system is mostly used for narrow-field objectives, such as astronomical telescopes and satellite cameras. Off-axial construction of a mirror system, however, can overcome the intrinsic problems of the conventional configuration, and could be used for wide-field applications [1].

In this study we present a new design approach for an image-space telecentric two-mirror system, corrected for spherical aberration, coma, and field curvature. We are interested in the two-mirror system as a possible candidate for a line-imaging objective of a hyperspectral imaging system [2]. Since an object-space telecentric spectrometer is used for the hyperspectral imaging system, image-space telecentricity is necessary for the two-mirror system.

Various two-mirror systems with corrected third-order aberrations have been known for a long time [3-6]. Because of image-space telecentricity, the conventional design approach for a two-mirror system can give an aplanatic design only, but is insufficient for designing a wide-field objective. From the analytic expressions of residual aberrations of the aplanatic design, we found that the primary mirror should be flat, to obtain a flat-field aplanatic design satisfying image-space telecentricity, but the conic constant of the primary mirror cannot be used to correct third-order aberrations in that case. We overcome this problem using the fourth-order aspheric deformation instead of the conic constant.

II. APLANATIC TWO-MIRROR SYSTEM

A conic surface with axial symmetry about the optical axis (z-axis) is defined by

where h is the incident height of a ray, r is the radius of curvature, and κ is the conic constant of the surface. The third-order aberrations of an optical surface are affected by the fourth-order term of h. The Maclaurin expansion of Eq. (1) yields

In modern optical design, the general aspheric surface is widely used to correct optical aberrations. Let us define a general aspheric surface that has fourth-order deformation on the sphere as follows:

In this case, the fourth-order deformation A can be expressed as

For a flat surface (c = 0) the conic constant does not give any effect on the surface, but A in Eq. (3) can be used to correct third-order aberrations.

A two-mirror system has five design parameters: two curvature radii (r₁, r₂), two conic constants (κ₁, κ₂), and the axial distance d between the two mirrors. Figure 1 shows a two-mirror system and its marginal ray. In Fig. 1(a), (h₁, h₂) are incident heights of the marginal ray, (u₀, u₁, u₂) are paraxial angles after reflection of the ray, and (n₀, n₁, n₂) are refractive indices of the medium after reflection. We adopt the sign convention of W. T. Welford [7, 8], by which the refractive indices are given as n₀ = 1, n₁ = −1, and n₂ = 1. If the incident heights (h₁, h₂) and the paraxial angles (u₀, u₁, u₂) are known, the curvature radii (r₁, r₂) and the axial distance d₁ are given by:

In Fig. 1, let us define the ratio of incident heights of the marginal ray as a₁, and the transverse magnifications of the surfaces (m₁, m₂), as the following:

Then the curvature radii and axial distance can be expressed as

In Eqs. (11)-(13), (m₁, m₂, a₁) determine the configuration of a two-mirror system, and (h₁, u₂) are scale factors corresponding to the aperture size and effective focal length of the system.

[FIG. 1.] Optical layout of a two-mirror system.

The third-order aberrations of a two-mirror system can be categorized by two parts: The main ones are the contributions of spherical surfaces, and the orders are the contributions of aspheric deformations. If the primary mirror is the aperture stop of the two-mirror system, then the spherical aberration S_I, coma S_II, astigmatism S_III and Petzval field curvature S_IV can be expressed as follows:

In Eqs. (14)-(17), H is Lagrange’s invariant, (s₁, s₂, s₃, s₄) are the contributions of spherical surfaces to the third-order aberrations, and (s_1c, s_2c, s_3c, s_4c) are the contributions of the conic constants (κ₁, κ₂).

Practically, we are interested in field curvature rather than Petzval field curvature. The third-order term of field curvature S_FC is

In Eqs. (14) and (15), S_I and S_II are linear functions of κ₁ and κ₂. The conic constants correcting S_I and S_II are given as follows;

The aplanatic design of a two-mirror system based on Eqs. (19) and (20) is the well known Ritchey-Chrétien (R-C) system [3]. The residual astigmatism S_III,R and the residual field curvature S_FC,R of the R-C system are

If we take a suitable combination of (m₁, m₂, a₁), one or two kinds of residual aberrations of the R-C system can be corrected additionally [3, 6].

III. ABERRATION CORRECTION OF A TELECENTRIC SYSTEM

3.1. Stop Position and Telecentric Condition

In this study, the two-mirror system we are designing requires image-space telecentricity. The aperture stop of a mirror system should be located where the stop does not interfere with incoming and outgoing beams. According to Fig. 2 there are five possible stop positions in a two-mirror system. To satisfy image-space telecentricity, the stop position should be the first focal point of the system, so positions ④ and ⑤ cannot be candidates. If we choose position ①, the sizes of the primary mirror M1 and secondary mirror M2 become large, which is undesirable. If we choose position ③, the tilting angles of M1 and M2 should be large enough to avoid ray obstructions by the stop. Hence, we choose position ②, the aperture stop at M1. In this case we do not need extra mechanical structure for the aperture stop, and the diameter of M1 can be minimized.

[FIG. 2.] Possible positions of the aperture stop in a two-mirror system.

Since M1 is taken as the aperture stop, the vertex of M1 should be the first focal point of M2, to satisfy image-space telecentricity. The separation between mirrors d₁ should be

where k₂ is the power of refraction of M2. In this case the total power of refraction K_T of the image-space telecentric two-mirror system is given by

From Eq. (24), the power of refraction of M1, k₁, does not affect K_T. k₁ only affects the back focal length (BFL) of the system. Eq. (23) can be rewritten as

which is the telecentric condition where the aperture stop is located at the primary mirror.

3.2. Aberration Correction for an Object at Infinity

If the object is located at infinity (u₀ = 0) and M1 has power of refraction u₁ ≠ 0, then the magnification m₁ is zero. In this case, from Eq. (21) the residual astigmatism of an R-C system is given by

By applying the telecentric condition of Eq. (25) to Eq. (26), we obtain the residual astigmatism of the image-space telecentric system as

If the two-mirror system has a specified power, the magnification m₂ cannot be infinite. Therefore, if the primary mirror has refracting power, the residual astigmatism of the image-space telecentric system cannot be corrected.

Let us consider the residual field curvature. If m₁ equals zero, the residual field curvature is

By applying the telecentric condition to Eq. (28), the residual field curvature of the telecentric system is given by

If the two-mirror system has a specified refracting power and M1 has refracting power, the magnification m₂ cannot be zero. Therefore, if the primary mirror is not flat, the residual astigmatism and field curvature of the image-space telecentric system cannot be corrected.

Let us consider an image-space telecentric two-mirror system having a flat primary mirror. In this case the magnification m₁ is 1, and the residual astigmatism of the RC system is

By applying the telecentric condition to Eq. (30), the residual astigmatism of the telecentric system is given by

This means that the residual astigmatism cannot be corrected.

Let us now consider the residual field curvature. Applying the telecentric condition to Eq. (22), the residual field curvature of the telecentric system is given by

If m₁ is equal to 1, from Eq. (32) the residual field curvature is

If the object is located at infinity and the primary mirror is flat (m₁ = 1), then m₂ is zero. The residual field curvature of the image-space telecentric system can be corrected.

As discussed, we can correct the residual field curvature of an image-space telecentric system by taking m₁ = 1 and m₂ = 0. However, the conic constants κ₁, κ₂, cannot be evaluated by Eqs. (19) and (20) in this case, and besides, for a flat surface the conic constant cannot be defined. Hence the fourth-order deformation term A must be used to correct the third-order aberrations.

Let us define the primary mirror M1 using Eq. (3), a general aspheric with fourth-order term A₁. Then κ₁ in Eq. (19) can be replaced by

By applying the telecentric condition to Eq. (34) and setting m₁ = 1 and m₂ = 0, A₁ correcting spherical aberration and coma is given by

Let us also consider κ₂ in Eq. (20). By the telecentric condition, (a₁−1) can be replaced with −m₂, and κ₂ can be expressed as

For the case of m₁ = 1, m₂ = 0, and a₁ = 1, the conic constant κ₂ is

M2 is an oblate ellipsoid. Using Eqs. (35) and (37), we can get an image-space telecentric two-mirror system corrected for spherical aberration, coma, and field curvature.

IV. OPTICAL DESIGN AND ABERRATION ANALYSIS

In the previous section, a two-mirror system having a flat M1 with fourth-order aspheric deformation, and an oblate ellipsoidal M2, can be corrected for three kinds of third-order aberration: spherical aberration, coma, and field curvature. Table 1(a) is an example design of an image-space telecentric two-mirror system with an axially symmetric configuration. Let us call this the initial design. Since M2 blocks all of the beams incident upon M1, the initial design is just a sample to show the results of the previous discussion. The initial design is a fast and wide-field mirror system with effective focal length of 100 mm, f-number of 2.0, and field angle of 6°. The third-order aberrations of the initial design are listed in Table 1(b). Spherical aberration, coma, and field curvature are corrected as expected. Figure 3 shows finite ray aberrations of the initial design. We can see a good correction of the third-order spherical aberration, and good balance between tangential and sagittal field curvature.

[TABLE 1.] Initial design of the telecentric two-mirror system (axially symmetric configuration)

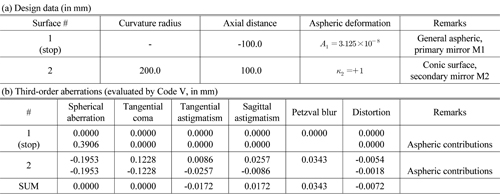
Initial design of the telecentric two-mirror system (axially symmetric configuration)

[FIG. 3.] Finite ray aberrations of the initial design.

Figure 4 shows the optical layouts of the decentered design (a) and the optimized design (b). The decentered design is an off-axial modification of the initial design, to avoid ray obstruction. M1 of the decentered design has a tilt angle of 16.5°. The line image along the horizontal direction (x-axis) can be accessed through the rectangular hole in M2. The optimized design is an improved version of the decentered design. The prescription for the optimized design is listed in Table 2. M1 in the optimized design is changed to a very weakly concave mirror. The fourth-order aspheric deformation A₁ and conic constant κ₂ are changed slightly.

[FIG. 4.] Optical layouts of the telecentric two-mirror designs: (a) decentered design; (b) optimized design.

[TABLE 2.] Optimized design of the telecentric two-mirror system (decentered and optimized for line image along the x-axis, in mm)

Optimized design of the telecentric two-mirror system (decentered and optimized for line image along the x-axis, in mm)

Spot sizes for the initial design (a), the decentered design (b), and the optimized design (c) are listed in Table 3. Figure 5 shows spot diagrams for the three designs. The residual wavefront aberrations of the three designs are listed in Table 4. The bold entries in Table 4 indicate the dominant residual aberrations. The spot diagrams shown in Fig. 5(a) and Zernike coefficients listed in Table 4(a) show that the primary astigmatism (Z4) is the dominant aberration of the initial design. From Fig. 5(b) and Table 3(b), quite large astigmatisms (Z4, Z6, and Z12) were introduced in the decentered system because of M1’s tilt. With optimization, the imaging performance of the optimized design improved, but the residual astigmatisms are the limiting factors. If we were to use anamorphic surfaces, then the residual aberrations might be corrected, but we use only axially symmetric surfaces, for easy fabrication and assembly.

[TABLE 3.] RMS spot size of the initial design, the decentered design, and the optimized design, for the best focus (in μm)

RMS spot size of the initial design, the decentered design, and the optimized design, for the best focus (in μm)

[FIG. 5.] Spot diagrams for the telecentric two-mirror designs: (a) initial design; (b) decentered design; (c) optimized design.

[TABLE 4.] Dominant wavefront aberrations of the two-mirror designs (in units of λ @ 632.8 nm)

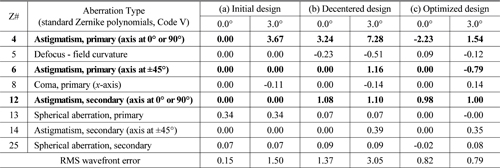
Dominant wavefront aberrations of the two-mirror designs (in units of λ @ 632.8 nm)

V. CONCLUSION

In this paper, we present a new design approach and example design for a two-mirror system with the aperture stop lying on the primary mirror M1, and which satisfies image-space telecentricity. From the analytic expressions for residual aberrations of the Ritchey-Chrétien system, we show that the residual astigmatism cannot be corrected if the object is at infinity, but the residual field curvature can be corrected by using a flat primary mirror M1. Since the conic constant cannot be defined for a flat M1, for correction we use the fourth-order aspheric deformation A₁ instead of the conic constant.

As an example, an optimized design for a two-mirror system that satisfies image-space telecentricity is presented. Since the initial design corrected for spherical aberration, coma, and field curvature has an axially symmetric configuration, the rays incident to the primary mirror M1 are obscured by the secondary mirror. Hence a tilted M1 is used for redesigning the two-mirror system to avoid ray obscuration. The optimized system is designed for a fast and wide-field line imaging objective of f-2.0 and 6° field of view. The effective focal length of the system is 100 mm. Even though the design uses only two axially symmetric mirrors (for easy fabrication and alignment), it shows quiet good performance, for a line imager. The RMS spot sizes of the optimized design are smaller than 22 μm.

참고문헌

1. Lebedeva G. I., Garbul A. A. 1994 Prospective aerospace reflective objectives [J. Opt. Technol.] Vol.61 P.610-614
2. Kim S. H., Kong H. J., Lee J. U., Lee J. H., Lee J. H. 2014 Design and construction of an Offner spectrometer based on geometrical analysis of ring fields [Rev. Sci. Instrum.] Vol.85 P.083108-083108-7
3. Wetherell W. B., Rimmer M. P. 1972 General analysis of aplanatic Cassegrain, Gregorian, and Schwarzschild telescopes [Appl. Opt.] Vol.11 P.2817-2832
4. Wyman C. L., Korsch D. 1974 Aplanatic two-mirror telescopes: a systematic study. 1: Cassegrainian configuration [Appl. Opt.] Vol.13 P.2064-2066
5. Wyman C. L., Korsch D. 1974 Systematic study of aplanatic two-mirror telescopes. 2: the Gregorian configuration [Appl. Opt.] Vol.13 P.2402-2404
6. Wyman C. L., Korsch D. 1975 Aplanatic two-mirror telescopes; a systematic study. 3: Schwarzschild-Couder configuration [Appl. Opt.] Vol.14 P.992-995
7. Welford W. T. 1986 Aberrations of optical system
8. Lee J. U., Yu S. M. 2009 Analytic design procedure of three-mirror telescope corrected for spherical aberration, coma, astigmatism, and Petzval field curvature [J. Opt. Soc. Korea] Vol.13 P.184-192

이미지 / 테이블

[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ FIG. 1. ] Optical layout of a two-mirror system.
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ FIG. 2. ] Possible positions of the aperture stop in a two-mirror system.
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ TABLE 1. ] Initial design of the telecentric two-mirror system (axially symmetric configuration)
[ FIG. 3. ] Finite ray aberrations of the initial design.
[ FIG. 4. ] Optical layouts of the telecentric two-mirror designs: (a) decentered design; (b) optimized design.
[ TABLE 2. ] Optimized design of the telecentric two-mirror system (decentered and optimized for line image along the x-axis, in mm)
[ TABLE 3. ] RMS spot size of the initial design, the decentered design, and the optimized design, for the best focus (in μm)
[ FIG. 5. ] Spot diagrams for the telecentric two-mirror designs: (a) initial design; (b) decentered design; (c) optimized design.
[ TABLE 4. ] Dominant wavefront aberrations of the two-mirror designs (in units of λ @ 632.8 nm)