



We present a graphical method for determining a pair of optical materials and powers to design an achromatic and athermal lens system with corrected Petzval curvature. To graphically obtain the solutions, a three-dimensional (3D) glass chart is proposed. Even if a particular material combination is unavailable, we can select an element suitable for a specific lens and continuously change the element powers of an equivalent single lens for aberrations correction. Thus, we can iteratively identify the materials and powers on a 3D glass chart. By designing a fisheye lens using this method, an achromatic and athermal system with flat Petzval curvature is obtained, over the specified waveband and temperature ranges.
When considering the design of an optical system that is capable of steady performance in various environmental conditions, the proper selection of materials and element power distribution is crucial. Such care is necessary since all optical systems generally suffer from chromatic and thermal defocuses, due to wide changes in wavelength and temperature.
For the visible and infrared wavebands, many graphical methods used to reduce such defocuses have been reported [1-7]. Although these methods provide achromatic and athermal solutions, they do not treat the refractive index of the material, which directly affects the field curvature. In particular, since a wide-angle system such as a fisheye lens has a large field curvature compared to normal or telephoto systems, the Petzval curvature of such a system should be reduced to some extent.
This study suggests a new graphical method to correct the Petzval curvature, in addition to the color and thermal aberrations, by introducing a three-dimensional glass chart to select an appropriate material and power combination. The chart consists of the inverse refractive index, the chromatic power, and the thermal power, which are the parameters that most significantly affect the Petzval curvature, color aberration, and thermal defocus, respectively.
In order to locate a system on this glass chart, an optical system with an arbitrary number of elements is reduced to a simpler doublet system that uses an equivalent single lens [7]. Thus, an optical system can be recomposed as a doublet of the specific lens and an equivalent single lens. First, by finding the proper element and material as a specific lens, and then by redistributing the element’s powers of an equivalent single lens, we can identify a pair of element’s material and power that satisfy the achromatic, athermal, and flat Petzval curvature conditions reasonably well.
Using this method to design a fisheye lens, we have found a good solution that has small color aberration and thermal defocus, along with a very slight Petzval sum. The Petzval sum and color aberration are reduced to −0.00064 mm−1 and −0.4 μm between the C- and F-lines, respectively. Moreover, the thermal defocus under a temperature change from −40°C to +80°C is found to be less than the depth of focus.
II. ZERO PETZVAL SUM, ACHROMATIC AND ATHERMAL CONDITIONS
As outlined above, the selection of the material and power distribution used for a lens element are very important in the design of optical systems, since these parameters significantly affect the aberrations. Among them, the Petzval curvature, chromatic aberration, and thermal aberration are representative aberrations that depend on the material’s properties and the power of a lens element. In an optical system composed of
where
The axial color aberration can be expressed as the difference between the back focal lengths of both wavelength extremes. Therefore, for the system to be achromatic, the system must satisfy Eq. (3) [4, 8-10]. The thermal aberration, as given by Eq. (4), is obtained by differentiating the total power
An equivalent single lens is used to effectively simplify the optical system with an arbitrary number of elements into a doublet system. That is, an optical system with
In this doublet system, which has total power
For a doublet system to be considered athermal, each element must have the power given in the following Eq. (13), which is obtained by solving Eqs. (9) and (12):
Inserting Eq. (13) into Eqs. (10) and (11) results in expressions for the zero Petzval sum and achromatic condition in a doublet system, which simultaneously satisfy the athermal condition:
III. AN ITERATIVE DESIGN METHOD BASED ON A THREE-DIMENSIONAL GLASS CHART
In order to graphically obtain a pair of materials satisfying Eqs. (14) and (15) for the doublet system, we plot two glass charts as shown in Fig. 1. In the first glass chart, the vertical axis corresponds to the thermal power
Many graphical methods which simultaneously correct the color and thermal aberrations exist [1-7]. However, although these methods provide achromatic and athermal solutions, they do not consider the correction of the field curvature, which is an extremely important aberration in a wide-angle system. To solve this problem, this study suggests a new graphical method to obtain an achromatic and athermal system with flat Petzval curvature by introducing a three-dimensional glass chart. This is one of the key points of this study.
Thus, to graphically obtain a pair of materials which satisfy Eqs. (14) and (15) simultaneously, we plot the three-dimensional glass chart composed of the
If this system is mounted in a housing material with a CTE of
The housing coordinate
As illustrated in Fig. 2(a), if any two elements,
On the other hand, although the coordinates of elements
Since the available optical and housing materials are limited, the proper material selection for the specific
First, the specific lens
Next, moving
Thus, by iterative application of this design approach, a multilens system with many elements can be achromatized, passively athermalized, and corrected for Petzval curvature.
As a design example using this proposed method, the redesign of an F/2 fisheye lens operating in the visible range from −40°C to +80°C is presented, as shown in Fig. 3. The initial fisheye lens is taken from an existing U.S. Patent [11], and redesigned to have nearly diffraction-limited performance, while keeping the first-orders intact. Tables 1 and 2 list the specifications and optical properties of the elements used in the initial fisheye lens. In Table 2, the labels G and P denote glass and plastic materials. In Fig. 3, the elements marked
[TABLE 1.] Specifications of the initial fisheye lens
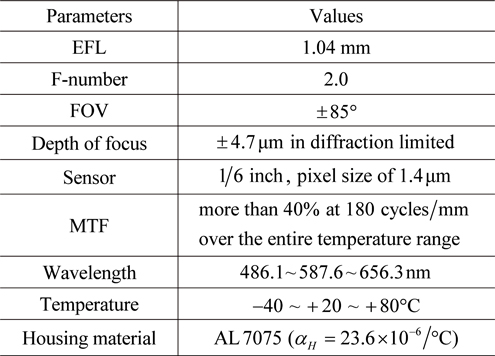
Specifications of the initial fisheye lens
[TABLE 2.] Optical properties of the initial fisheye lens elements
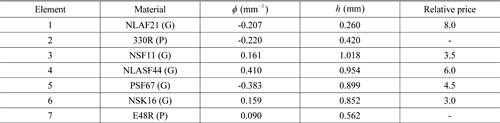
Optical properties of the initial fisheye lens elements
In this system, the color aberration between the C- and F-lines is evaluated to be +8.0 μm. Additionally, the Petzval sum is still quite large at a value of +0.0232 mm−1. Among the available housing materials, AL7075 with a CTE of
The thermal properties of this system are shown in Fig. 4. As seen in Fig. 4(a), the effective focal length of this system is thermally unstable from −40°C to +80°C. The label HML that appears in the figure corresponds to the housing material length (i.e., the length of the housing), while the label EFL corresponds to the effective focal length. The thermal defocus, which is expressed as Δ = HML − EFL, ranges from −10.8 μm to +11.4 μm at the two extremal temperatures, which is greater than the depth of focus. This large thermal defocus leads to an unstable modulation transfer functions (MTFs) at frequencies greater than 100 cycles/mm, as shown in Figs. 4(b)-4(d).
A number of doublet systems can be created from the elements of the initial optical system. In Table 3, the first column lists the seven possible choices of the specific
From the small values of Δ
In a wide-angle lens, the front lens
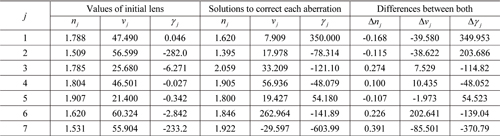
Optical material properties of the j-th element and solutions to correct three aberrations in the initial fisheye lens (γ is measured in units of ×10?6/°C)
In the two glass charts of Fig. 6, the current glass NLAF21(788.475) used for
By replacing the glass used in the first lens with NF2, the Petzval curvature is corrected, and subsequently, moving
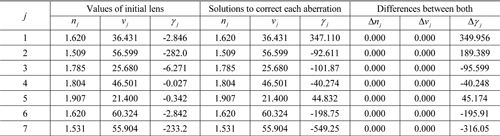
Optical material properties of the j-th element and solutions to correct three aberrations in a temporary fisheye lens (γ is measured in units of ×10?6/°C)
Since the thermal aberration has not yet been corrected, each Δ
Here, while is moved to
In order to have an athermalized system, the CTE of a housing is required to be
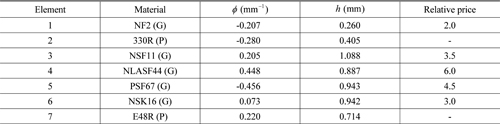
Optical properties of the elements in the achromatic and athermal fisheye lens with corrected Petzval curvature
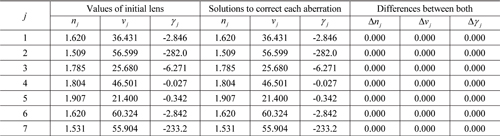
Optical material properties of the j-th element and solutions to correct three aberrations in the final fisheye lens (γ is measured in units of ×10?6/°C)
From the new approach demonstrated in this example, we see how the three-dimensional glass chart may be utilized efficiently in order to yield achromatic and athermal solutions that have corrected Petzval curvature. This new design concept is a key aspect of this study.
When the redesigned lens elements are housed in an AL7075 material, the thermal defocus (Δ= HML − EFL) from −40°C to +80°C is significantly reduced to less than 3.7 μm, as illustrated in Fig. 9(a). We note that with this design the sign of ΔEFL is the same as that of ΔHML, which effectively reduces the thermal defocus across the entire temperature range. Thus, the thermal defocus due to a change in temperature is less than the depth of focus of ±4.7 μm. In addition, the color aberration between the C- and F-lines is reduced from +8.0 μm to −0.4 μm, which is much less than the depth of focus. Moreover, the Petzval sum also undergoes a significant reduction, decreasing from +0.0232 mm−1 to −0.00064 mm−1. Here, since the initial fisheye lens was approximated as a thin lens system, and the three aberrations were subsequently corrected by changing the glass and redistributing the element powers, the final redesigned lens has a slight, but non-zero aberration.
Figure 9 shows the modulation transfer functions (MTFs) at various temperatures. In comparison to those shown in Fig. 4, the MTFs of a fisheye lens corrected for three aberrations are much more stable than those of the initial lens over the specified waveband and temperature ranges. In addition, the MTFs at the maximum frequency of 180 cycles/mm are greater than 40% for all fields. Even though it is an extremely wide-angle system, our redesigned system reduces the distortion of the initial lens from −10% to −8%, when evaluated using the equi-angle mapping (
In order to correct the three aberrations that are most significantly affected by the material properties and the element power distribution in an optical system, this study suggests a new graphical design method based on a three-dimensional glass chart to iteratively obtain the optimal material and power combinations. In summary, in order to correct the Petzval curvature in an achromatic and athermal lens, a two-dimensional glass chart is expanded into a three-dimensional glass chart by the introduction of the inverse refractive index axis. In comparison to previous glass charts, the iterative design method that results from the use of this expanded chart graphically provides the desired materials and element powers to simultaneously correct the three basic aberrations.
Although a particular material combination may not exist, the proposed method effectively provides athermal and achromatic solutions with corrected Petzval curvature. By utilizing this method to design a fisheye lens, we have obtained an optical system that has a flat Petzval curvature, small color aberration and thermal defocus. The proposed iterative design method outlined here is expected to serve as a useful way to find optical system solutions with a three-dimensional glass chart.







































