



Most of the studies on the hydraulic characteristics of wave-current interaction have used 2-D hydraulic experiments or 2-D numerical simulations. However, it is difficult to understand the wave-current interaction found in actual estuaries using these. Therefore, a numerical water tank was constructed in this study to perform simulations involving a 3-D river mouth. The result showed a change in the water surface at the river mouth from the wave-current interaction. With an increase in the ratio (Vc/Ci) between the river current and wave celerity, the wave height and mean water level of the river increased at the wave and current meeting point. A higher Vc/Ci caused a stronger wave-current interaction and increased the turbulence kinetic energy. Thus, the wave height attenuation became larger by the wave-current interaction with a higher Vc/Ci. In addition, it was possible to understand the flow characteristics in the vicinity of the river mouth as a result of the wave-current interaction using the mean flow and mean time-averaged velocity at the mid-cross section of river.
하구지역은 물리적 성질이 서로 다른 파랑과 흐름, 해수와 담수가 충돌하는 매우 역동적인 곳이다. 이 지역의 수리역학적 관계는 상당히 복잡하며, 이 수리특성을 해석하기 위해서는 파랑과 흐름의 상호작용 기구를 이해하여야 한다. 이에 과거부터 파랑-흐름 상호작용에 관한 기초적인 연구들이 많이 수행되었다.
초기에는 포텐셜 이론에 근거한 연구들이 주로 수행되었으며, 파랑-흐름 공존장에서 진행파의 파고가 서서히 상승하다가 임계점에 이르러 쇄파가 발생하게 된다. 이로 인해 파랑에너지가 감쇠되는 것으로 보고되고 있다(Zhao and Faltinsen, 1988; Baddour and Song, 1990; Isaasson and Cheung, 1993; Lin and Hsiao, 1994). 그러나 몇몇 수리실험에서 파랑-흐름 상호작용에 의한 파고가 점진적으로 감소하는 상반되는 현상이 나타나고 있다(Iwasaki and Sato, 1971; Sakai and Saeki, 1984; Umeyama, 2005; Komatsu, 2005; Lee, 2012). 또한 근래에는 강비선형의 Navier-Stoke(N-S) 방정식 모델의 수치계산에서도 파랑-흐름 상호작용에 의한 파고감쇠 현상이 나타나고 있다(Mizutani et al., 2002; Lee et al., 2011; Lee et al., 2012a). 다른 한편에서는 파랑-흐름 공존장의 유동구조를 해석하기 위하여 수치모델들(Olabarrieta et al., 2010; Teles et al., 2013; Son and Lynett, 2014)이 개발되었으며, 기존의 수리실험결과와 비교하여 높은 일치도를 나타내었다. 하지만 이 연구들은 파랑-흐름 공존장의 유동구조만을 분석하고 있을 뿐, 파랑변형에 대해서는 심도 깊은 논의가 없다.
국내에서는 파랑-흐름 상호작용에 관한 연구가 거의 수행되고 있지 않다가, 최근에 Lee and Hur(2014)이 무반사로 파랑과 흐름을 생성할 수 있을 뿐만 아니라, 파랑-흐름 공존장에서 지형변동까지 해석할 수 있는 수치모델을 개발하였다. 그리고 Lee and Hur(2016)는 이 수치모델을 적용하여 파랑-흐름 상호작용에 의한 파고감쇠 현상과 난류강도 특성을 분석하여, 그 연관관계를 면밀히 고찰하였다. 그러나 실제 파랑과 흐름이 공존하는 하구지역의 파랑변형을 Lee and Hur(2016)의 2차원적인 검토로 이해하기에는 부족한 점이 너무나 많다.
하구지역의 수리특성을 해석하기 위한 소수의 실험적 연구들이 진행되었다. 대표적으로 Smith et al.(1998)는 하구지역에서 파랑-흐름 상호작용에 의한 파랑변형특성을 조사하였다. Lee et al.(2012b)는 경사입사파랑과 하천흐름과의 상호작용에 의한 파고분포, 저층흐름 특성을 조사하였다. Lee(2012)는 하구에서 하천수로로 유입되는 파랑의 변형특성을 난류운동에너지와 연관하여 조사・분석하였다. 그리고 수치적인 연구들은 대부분 수심 적분의 평면모델(Shi et al., 2001; de Brye et al., 2010)이거나,
본 연구에서는 하구지역에서 파랑-흐름 공존장의 3차원적 수리특성을 수치적으로 분석하기 위하여 파랑-흐름 상호작용에 의한 파고 감쇠기구 분석에 적용된 HYMO-WASS-3D(Lee and Hur, 2014)를 이용한다. 그리고 3차원 하구지형을 고려한 수치시뮬레이션을 통하여 시간파형, 파고분포, 난류운동에너지, 단면/평면적 유속분포를 고찰하여 파랑-흐름 상호작용에 의한 3차원 흐름구조를 파악한다.
본 연구에서는 파랑과 흐름이 공존하는 하구지역의 수리특성을 이해하기 위하여 파랑-흐름 상호작용에 의한 파고감쇠 현상모의에 적용된 HYMO-WASS-3D(Lee and Hur, 2014)를 이용한다. 이 수치모델은 PBM(Porous body model)과 VOF(Volume of fluid)법 기반의 3차원 N-S solver로써 파랑과 흐름을 무반사로 생성할 수 있을 뿐만 아니라, 파랑-흐름 비선형 상호간섭을 직접 해석할 수 있다. 그리고 아격자(Sub-grid) 크기의 난류를 고려하기 위하여 Germano et al.(1991)과 Lilly(1992)가 제안한 동적 와동점성모델을 이용하고, 자유수면의 표면장력은 CSF(Continuum surface force)모델(Brackbill et al., 1992)로부터 추정된다.
기초방정식은 3차원 비압축성・점성유체에서 파랑과 흐름을 무반사로 발생시킬 수 있는 소스항이 포함된 연속방정식 (1)과 투과성 구조물 내부의 유체저항을 고려한 수정된 N-S 운동량 방정식 (2)로 구성되어 있다.
여기서
나머지 상세한 수치해석방법에 대해서는 Lee and Hur(2014, 2016)를 참조하기 바란다.
본 연구에 적용하는 HYMO-WASS-3D는 Lee and Hur(2014)에 의해 개발되었으며, 파랑-흐름 상호작용에서 파랑변형특성(파고 감쇠 현상)에 관한 Iwasaki and Sato(1971)의 수리모형실험결과를 매우 잘 재현하였다. 그리고 Umeyama(2005)가 실험에서 나타낸 파랑-흐름 순방향, 역방향 상호작용에 따른 평균유속의 연직분포들과도 높은 일치도를 나타낸다. 게다가 파랑-흐름 순방향 및 역방향 공존장에서 해저파이프라인 저면의 세굴현상까지도 Kim et al.(2008)의 실험결과를 잘 나타내고 있다. 따라서 HYMO-WASS-3D는 파랑-흐름 상호작용에 관하여 충분히 타당성과 유효성이 입증된 것으로 판단된다. 검증에 대한 상세한 사항들은 Lee and Hur(2014)를 참조하기 바란다.
파랑과 하천유속 변화에 따른 하구 주변의 3차원 동수학적특성을 파악하기 위하여 Fig. 1과 같은 3차원 수치수조를 구성한다. 무반사로 파랑과 흐름을 만들어 낼 수 있는 무반사 생성시스템을 적용하고 있으며, 이 시스템은 입사파랑과 흐름을 일정하게 생성할 수 있는 원천, 서서히 에너지를 흡수하는 부가감쇠 영역, 수치수조 밖으로 에너지를 완전 방사할 수 있는 개경계 조건(Open boundary)으로 구성된다. 수심(
본 수치모의 입사조건은 Table 1과 같으며, 총 36가지 조건이다. 외해로부터 3가지의 파고(
[Table 1] Incident conditions of wave and current used for numerical simulations
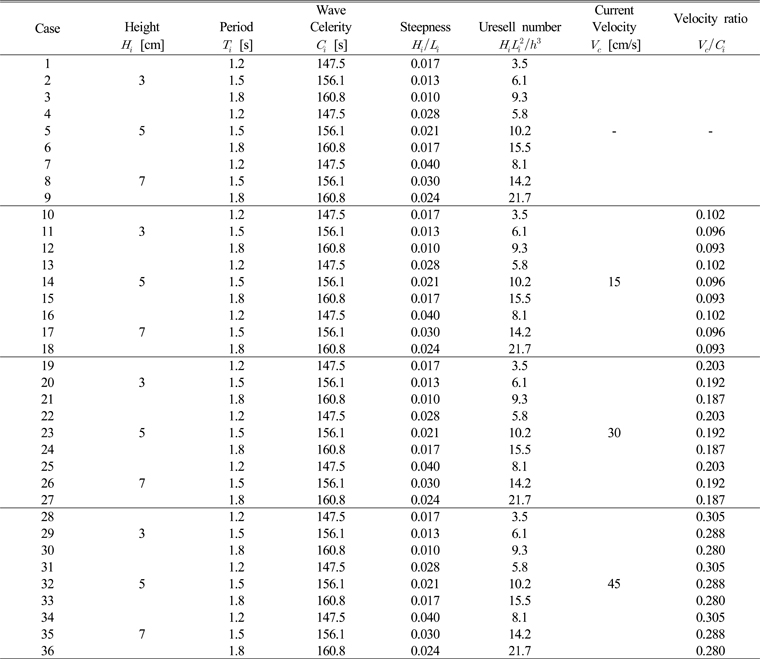
Incident conditions of wave and current used for numerical simulations
3.1.1 수면형 분포
Fig. 2는 하구 주변의 수면형을
Fig. 2로부터 하천흐름이 존재하는 (b)의 경우가 그렇지 않은 (a)의 경우에 비해 하구 전면에서 높은 수위분포를 보인다. 특히 파봉이 하구로 유입될 때에 흐름과의 상호작용에 의해 파봉의 높이가 상승하는 현상이 발생한다. 이 현상은 3차원 하구지형을 적용한 Lee(2012)의 수리모형실험과 Lee and Hur(2016)의 2차원적 해석결과에서 나타낸 것과 같이 파랑과 흐름이 만나는 지점에서 파고가 상승하는 현상으로 이해된다. Fig. 2는 대표적인 계산결과만을 비교하여 나타낸 것이며, 입사파랑 및 하천흐름 조건에 따라 다양한 형태의 파동장 및 유동장이 발생한다. 이에 대한 심도 깊은 논의는 후술하는 파고분포, 흐름분포 그리고 난류분포에서 면밀하게 고찰하기로 한다.
Fig. 3은 하천유속과 입사파속과의 비(
Fig. 3으로부터
Fig. 4는 하천 중앙단면(
Fig. 4로부터 Fig. 3에서 확인한 것과 같이
한편 단면 2차원적인 수리실험(Lee, 2012)과 수치실험(Lee and Hur, 2016)에서 측정되었던 파랑-흐름 공존장에서의 파랑반사는 뚜렷하게 나타나지 않는다. 이것은 3차원적 하구지형과 투과성 해빈을 고려하였을 때에는 파랑과 흐름의 에너지가 분산되기 때문에 단면 2차원적인 조건과 차이를 나타내는 것으로 판단된다.
Fig. 5는 하구 주변에서 파랑-흐름 상호작용에 따른 평균 난류 운동에너지()의 3차원 분포를 나타낸 것이다. 여기서 는 식 (4)와 같이 정상상태에서 10주기 평균한 것으로 난류운동에너지는 Christensen(2006)이 제안한 식 (5)와 식 (6)을 적용하여 계산한다. Fig. 5에서 (a)는 Case 5로 하천으로부터 흐름이 유입되지않는
여기서
Fig. 5로부터 모든 경우에서 유체활동이 매우 활발한 포말대(Swash zone)에서 상대적으로 강한 가 발생함을 알 수 있다. 여기에 파랑-흐름 상호작용에 따른 단면 2차원적 난류구조를 분석한 수리실험(Umeyama, 2005) 및 수치실험(Lee and Hur, 2016)에서와 같이 수면부근의 평균 난류운동에너지가 크게 나타날 뿐만 아니라,
3.3.1 하천유속의 영향
Fig. 6은 하천유속과 파속과의 비(
여기서
Fig. 6 (a)로부터 하천흐름이 없는 경우에 해빈에 의한 파랑반사의 영향으로 부분중복파동장의 유속분포가 형성되는 것을 알 수 있다. 그러나 하천흐름이 존재하는 (b)와 (c)에서는 흐름의 영향으로 부분중복파동장에 의한 유속분포가 발생하지 않을 뿐만 아니라,
Fig. 7은
Fig. 7로부터 모든 수치실험결과에서 정수면 부근에서는 외해에서 하천으로 유입되는 유속이 나타난다. 그리고 정수면의 아래층에서는 하천에서 외해로 빠져나가는 유속이 형성되며, 하천유속이 클수록 빠져나가는 유속도 증가하는 것을 확인할 수 있다. Fig. 7 (a)와 같이 파랑만 유입될 경우 모래해빈의 경사에 의한 천수효과로 인해 정수면 위에서도 유속벡터가 나타난다. 이 유속벡터는 하천유속이 증가할수록 파랑-흐름 상호작용에 의한 파고의 상승효과가 더해져 하천입구로부터 멀리 떨어진 영역까지 확장되는 것을 알 수 있다. 게다가 해빈의 경사면 상에 생성된 순환류는
3.3.2 입사주기의 영향
Fig. 8은 입사주기(
Fig. 8로부터
Fig. 9는
Fig. 9로부터 외해에서 하천으로 향하는 정수면 부근의 유속이
3.3.3 입사파고의 영향
Fig. 10과 Fig. 11은
Fig. 10으로부터
Fig. 11로부터
이로써 기존의 단면 2차원 수리/수치실험에서 논의할 수 없었던 파랑-흐름 상호작용에 의한 3차원 수리특성을 이해할 수 있었다. 특히 파랑과 흐름이 공존하는 하구지역에서 파랑과 흐름 조건에 따른 3차원 흐름특성을 고찰할 수 있었다.
본 연구에서는 하구지역에서 파랑-흐름 상호작용에 의한 3차원 흐름특성을 분석하기 위하여 수치모형실험을 수행하였다. 수치실험에는 파랑-흐름 상호작용에 의한 파고감쇠 기구분석을 수행한 3-D N-S solver(Lee and Hur, 2016)를 이용하였다. 수치실험에서는 실제와 유사한 3차원 하구모형을 고려하였으며, 하천유속, 입사파고, 입사주기에 따른 흐름특성을 고찰하였다. 이로부터 얻어진 주요한 수치해석결과를 기술하면 다음과 같다.
(1) 파랑-흐름 상호작용에 대한 기존의 단면 2차원적인 수리 및 수치실험에서 확인할 수 없었던 하구 주변의 3차원적 수면형 및 파고분포를 확인할 수 있었다.
(2) 파랑-흐름 상호작용에 의한 3차원적 난류구조 및 난류운동에너지를 이해할 수 있으며,
(3) 파랑-흐름 공존장에서 정수면 부근에서는 외해에서 하천으로 유입되는 유속, 정수면의 아래층에서는 하천에서 외해로 빠져나가는 유속이 발달하였다.
(4) 파랑-흐름 상호작용에서 파속 또는 파랑작용에 의한 수립자 속도가 커질수록 하천에서 외해로 빠져나가는 흐름유속이 작아지는 경향을 나타낸다. 그리고 하천유속이 커질수록 하천 수로에서는 하천으로 유입되는 유속이 약해지는 것을 알 수 있었다.
이로써 파랑과 흐름이 공존하는 하구 주변의 전반적인 수리특성을 파악할 수 있었다. 향후에는 하구지형을 고려한 3차원 실험 또는 현장관측과 비교・검증을 통해 수치모델을 수정 및 보완해 나갈 예정이다. 나아가 실험실 조건에서 벗어나 실제 하구를 대상으로 파랑-흐름 상호작용과 하구밀도류를 함께 모의한다면, 하구지역의 수리특성을 수치적으로 분석하는 데 크게 기여할 것으로 판단된다.




















