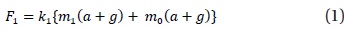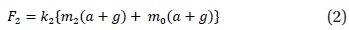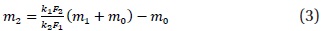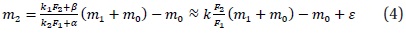In this study, a new idea for developing a space scale for measuring mass in a microgravity environment was proposed by using the inertial force properties of an object to measure its mass. The space scale detected the momentum change of the specimen and reference masses by using a load-cell sensor as the force transducer based on Newton’s laws of motion. In addition, the space scale calculated the specimen mass by comparing the inertial forces of the specimen and reference masses in the same acceleration field. By using this concept, a space scale with a capacity of 3 kg based on the law of momentum conservation was implemented and demonstrated under microgravity conditions onboard International Space Station (ISS) with an accuracy of ±1 g. By the performance analysis on the space scale, it was verified that an instrument with a compact size could be implemented and be quickly measured with a reasonable accuracy under microgravity conditions.
A space scale is a measuring instrument for determining the mass of live specimens made of solid, semi-solid, and liquid materials (in containers) with a mass of less than 3 kg in a space environment (especially in microgravity environments (or ‘zero-gravity’)) on board the International Space Station (ISS). The life science studying a long-term human stay in space and the material science studying industrial applications are important research fields on the ISS. For these research fields, basic instruments for measuring mass such as space scale are required, especially accurate and compact instruments to be handled by astronauts because general balances based on the gravity effect on ground do not work in the microgravity environment.
Several studies on the mass measurement under the microgravity conditions are reported: a vibration type using a characteristic frequency and an inertial force type using centrifuging (Rivetti et al. 1999) and the law of the momentum conservation (Fujii 2006). By using the vibration method, the characteristic frequency according to the object mass is measured with a high accuracy. However, the change in the frequency is influenced not only by the mass, but also by the volume, density, material quality, vibration field that is not constant according to the location, and method of installing the specimens. By using the inertial force type (Rivetti et al. 1999), the specimen mass is measured by using centrifugal force experienced by the mass caused by rotating the specimen. This centrifuge system can obtain a constant acceleration field through long specimen rotation. However, it is not easy to estimate the center of mass used in numerical expressions because the center of gravity varies according to the volume, density, and shape of the specimen (Fujii 2006). Long measurement duration also can be stressful for living specimens such as lab rats. By using an inertial system using the law of conservation of momentum (Fujii 2006), the specimen mass is estimated by measuring the inertial force by means of acceleration. It is possible to quickly measure the force with high accuracy based on Newton’s law of motion,
In this paper, the proposed and implemented instrument is a low-capacity inertial balance (between 0 g and 3 kg) based on the inertial system. It is a compact, reliable, and simple system which can provide fast measurements with a reasonable accuracy. As for the last two applications, the systems require a stable motion and a uniform acceleration to estimate the mass. This system compares the inertial forces between the specimen and a reference object on the same acceleration plate simultaneously, hence the acceleration term is eliminated in the calculation algorithm. The performance test was conducted in the microgravity environment onboard the ISS as part of the scientific experiments of the Korean astronaut program in April 2008.
2. SPACE SCALE DESIGN AND IMPLEMENTATION
2.1 Conceptual Measurement Scheme
In the measurement scheme of the space scale and the conceptual method demonstrated in Fig. 1, the method of the law of momentum conservation (Fujii 2006) is used by applying mechanical acceleration to some specimens. However, this method is simpler and easier than the former method using the law of momentum conservation because the mass is calculated by measuring the inertial force of the reference object (known value) and the specimen (unknown value). First, two load-cells, which are sensors for the load and the force transducer, are mounted onto the same acceleration plate that moves up and down by using a DC motor. Then the specimen and the reference object are placed on each load-cell. The load-cells, the specimen, and the reference object are in the same inertial system; hence, they are under the same acceleration conditions. When the objects undergo accelerated motion, the specimen and the reference object measured by the load-cells, based on the Newton’s laws of motion, in terms of the inertial forces by the equations given below.
In expressions (1) and (2),
In expression (3), the reference mass
2.2 Space Scale Implementation
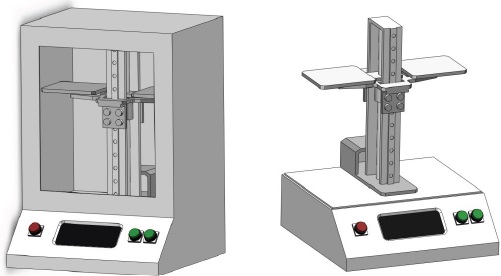
The concept, design, and hardware development of the space scale is demonstrated in this subsection. Figs. 2 and 3 show the 3D design of the space scale and the real space scale hardware for the outer and the inner views, respectively. The main specifications of the space scale are indicated in Table 1. The longer the length of motion is, the more data we can obtain. However, because there are some constraints on the mass and volume of the apparatus for the experiments conducted on the ISS, the range of motion is chosen as approximately 15 cm, which is the minimum length required to obtain sufficient acceleration.
[Table 1.] Specifications of the space scale

Specifications of the space scale
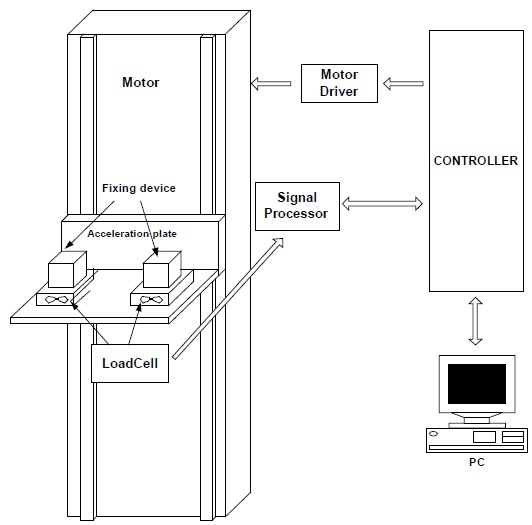
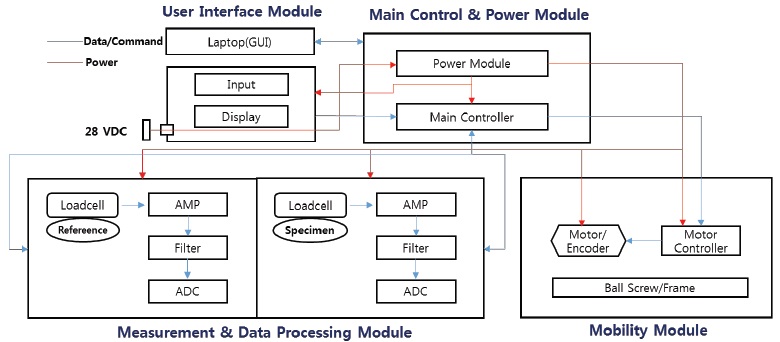
The space scale mainly comprises the mobility module for the accelerated motion, measurement and data processing modules for measuring the inertial forces and processing the analog data, main control and power module for controlling the system and the communication electrically, and user interface module for operating the system, as shown in the block diagram of Fig. 4.
As mentioned before, the specimen and the reference object are mounted onto each load cell plate. The mobility module has the DC motor as the motion source, ball screw to change the rotational motion of the motor into linear motion, and motor controller including an encoder that controls a velocity of the motor. The mobility module generates an inertial force by driving the DC motor and accelerates the specimen and the reference object to 0.4 G (gravity, 1 G = 9.8 m/s2). The load cell and acceleration plates are interfaced with the ball screw and motor and move approximately 15 cm up and down along the ball screw for 0.4 sec. Hence, the specimen and the reference object mounted onto the plates are in the inertial system under the same acceleration conditions.
The measurement and data processing module comprises two load cell sensors and a signal-processing component for the data measured by the load cells. A highly sensitive load cell as the transducer for the conversion of force into an electrical signal measures the resistance change from the force and the load by using an embedded Wheatstone bridge circuit and generates an analog signal in proportion to the momentum change of the specimen and the reference masses. In this study, a commercial single point load cell was manufactured only for the space scale and the accuracy of the load cell was improved in a measurement range of 3 kg, not considering the space and microgravity conditions.
To transfer the corresponding signals to the main control module, which calculates the specimen mass , the analog signals of the specimen and of the reference object are amplified, filtered, and converted into digital signals by each signal processor (amplifier, filter, Analog to Digital Converter (ADC)), as shown in Fig. 4.
The main control & power module manages and controls all functions of the space scale, such as motor control, signal processor control, data storage, and calculation of the mass, by using the space scale algorithm. The power distribution unit with a regulator and a DC-to-DC converter supplies the necessary electrical power to all devices in the space scale. The space scale is operated by the user interface module having all application software by Graphical User Interface (GUI) in a laptop.
2.3 Preliminary Test and Calibration of Space Scale
As mentioned above, the main control module monitors the present motor state and controls the input acceleration motion of the motor. In the profile of the motor motion, the motor linearly accelerates for approximately 0.2 sec and achieves an acceleration of greater than 0.4 G (approximately 4 m/s2).
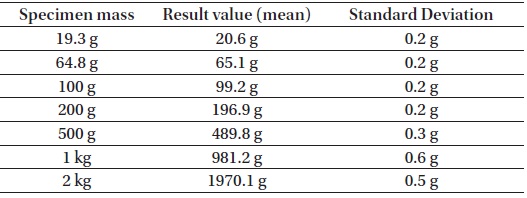
By using the proposed profile of the motor motion, preliminary tests were conducted in the space scale. A solid metal object of 100 g mass is used as the reference object and solid objects with a mass of 19 g ~ 2 kg are used as the specimens. From the result of several tests demonstrated in Table 2, it was shown that this system had an error of 0.46%−6.7%, which is larger than expected, and the system of dispersion is more than the design requirements with a standard deviation of each measurement of 0.2 ~ 0.6 g.
To compensate these error terms we approximately expanded the original formula with the final term in expression (4).
[Table 2.] Preliminary test results
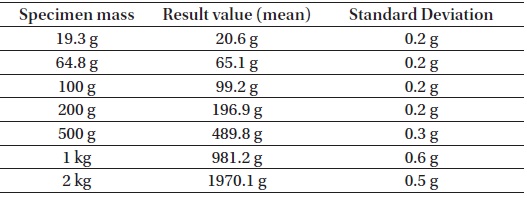
Preliminary test results
We applied the calibration function to the space scale, and the parameters
The calibration is conducted as follows. The minimum mass in the measurement range is used as the specimen, and the ratio of
3. GROUND & MICROGRAVITY EXPERIMENT
To demonstrate the performance and accuracy of the space scale, experimental tests were performed on the ground and in space. In the experiments, solid metallic objects were used as the specimens and the reference objects to verify the accuracy. In this section, all test results are applied to the calibration function.
3.1 Performance Test on Ground
The performance tests on the ground were performed in the vertical and horizontal states of the space scale, from which we could check the effects of gravity under different conditions, as shown in Fig. 5. Table 3 shows the test results for the experimental test conducted 20 times for each specimen on the ground. The accuracy of the space scale on the ground is approximately 0.05% for a specimen with a mass of 2 kg, and the repeatability is good, as seen in Table 3. There are not any effects due to the direction of gravity, as expected from the results for the vertical and horizontal states.
[Table 3.] Ground test results

Ground test results
3.2 Performance Test under the Microgravity Condition
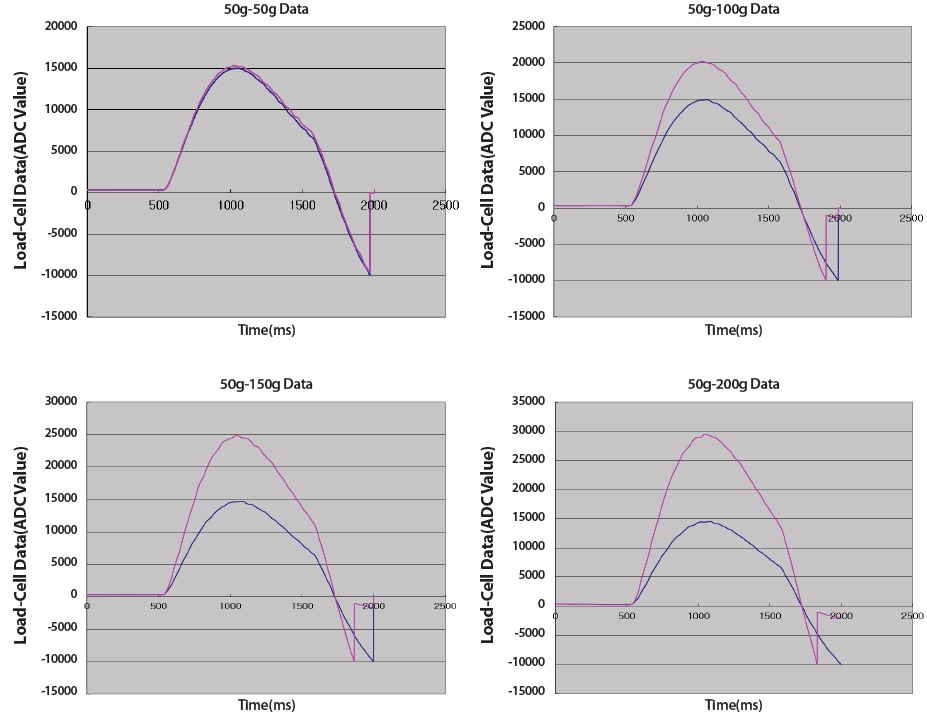
The performance tests on the ISS were conducted by Korean astronaut (Fig. 6). The space scale was tested by using solid metallic samples with masses of 50, 100, 150, and 200 g, respectively, and solid samples with masses of 19 g and 69 g. Fig. 7 shows the ADC value profile of the measurement data from the load cell for specimens with masses of 50 g−100 g. The data in the acceleration section (approximately 600−1,600 msec) are used for calculating the specimen mass.
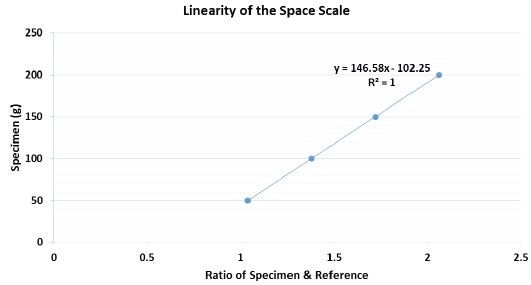
Fig. 8 shows that the measured data of the space scale had almost linear characteristics with the first order expression. The x-axis represents the ratio of the measured data
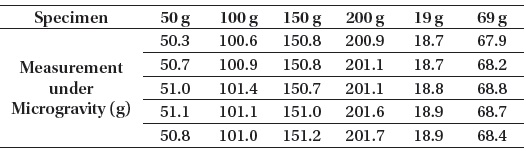
The test results are summarized in Table 4. As can be seen from the table, the accuracy is approximately ± 1 g and the repeatability of the system is good although the number of measurements is not much. Actually, the space scale was implemented for measuring the mass of objects with masses of 0 g ~ 3 kg, but solid specimens with masses of 0 g ~ 200 g were used because the space scale was initially made for monitoring small weights of lab rats (approximately 20 g ~ 100 g). Furthermore, in the experiments conducted on the ISS there were the weight limit for cargo to carry to the ISS and the time limit for astronauts to conduct these experiments. However, we verified our theory and, from the obtained results, we could see the possibility of the space scale as a viable space balance. .
[Table 4.] Microgravity experiment results (Kim et al. 2009).
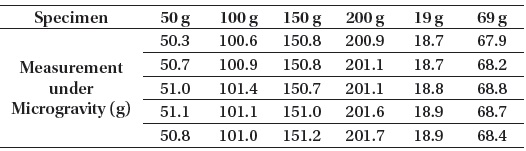
Microgravity experiment results (Kim et al. 2009).
This study focusses on a novel methodology for measuring mass under microgravity conditions and the implementation of the space scale. We proposed new methods to measure mass in microgravity conditions using the inertial properties of objects. Using the law of momentum conservation, we designed a space scale as a space balance by comparing the inertial forces between the reference object and the specimen. We implemented the space scale instrument using this new idea, and it was tested on the ground and onboard the ISS in the microgravity environment.
From the results of the performance tests for the space scale conducted on the ground and on the ISS, we found the space scale to be accurate and efficient. The space scale is accurate up to approximately 1 g based on the tests conducted on the ISS and error tolerance of 0.05% for a specimen of 2 kg mass in the tests conducted on the ground. Measurements can be made within 2 sec. Therefore, we could demonstrate that a fast, compact, and accurate instrument under the microgravity conditions on board the ISS was practical.