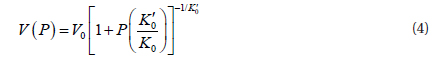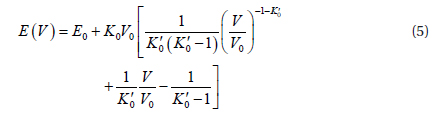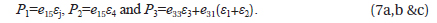Piezoelectric materials have a very important role in modern industries and are widely used as key materials in transducers, resonators, filters, and sensors. Discovered in 1880 by Pierre and Jacques Curie, piezoelectricity is a phenomenon whereby material becomes electrically polarized upon the application of stress. Complex insulating perovskite alloys are currently of great interest for use based on the exceptional piezoelectric properties. Examples include the Pb(Zr1−xTix)O3 (PZT) solid solutions that are currently used in piezoelectric transducers and actuators, and most recently, the class of PbMg1/3Nb2/3O3−PbTiO3 (PMN-PT) and PbZn1/3Nb2/3O3−PbTiO3 (PZN-PT) materials which, when synthesized in single-crystal form, exhibit remarkably large piezoelectric constants and maximum strain levels. These materials promise dramatic improvements in the resolution and range of ultrasonic and SONAR listening devices. Moreover, new piezoelectric materials with excellent piezoelectric response combined with high temperature operation capabilities are currently sought. A fundamental understanding of factors that influence the piezoelectric properties of materials are of high scientiflc and technological value, but remains difficult to forecast.
Since the 1970s, scientists have persisted with efforts to make theoretic effort forecasting feasible. Due to rapidly increasing calculation speed and memory capacity of supercomputer and establish of modern polarization theory, direct quantitative calculation of piezoelectric coefficient of some relatively simple piezoelectric systems and qualitative forecasting of piezoelectric coefficient of some ferroelectric system from first principles are now possible. Based on the Kohn-Sham formulation [1], the density-functional theory (DFT) [2] has been used to calculate large systems where
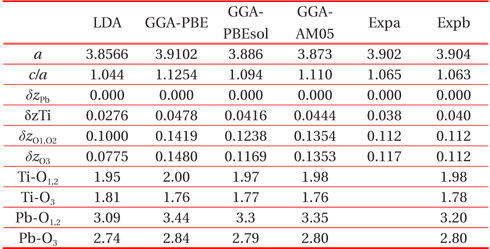
Most previous DFT studies have employed the local density approximation (LDA) and the generalized gradient approximation (GGA) functionals to explain the exchange-correlation energy. The gradient corrected Pedrew-Burke-Ernzerhof (PBE) [4] functional has been regarded as the standard GGA. For the lattice constant of solids, which is one of the most important factors in predicting mechanical and piezoelectric properties, LDA clearly underestimates the lattice constants whereas the GGA-PBE overestimates lattice constants to a similar degree. This discrepancy between the experiments and the predictions is intensified for the solids having d- and f-valence electrons, such as transition metals and their oxides. Recently, to improve the lattice constants of solids, new GGA functionals (PBE for solids, PBEsol [5] and AM05 [6]) have been suggested, and were shown to improve over PBE for various solids including transition metals.
In the present work, under the DFT, we investigate the physical properties of PbTiO3 (PT), which is one of the simplest ferroelectric oxide. Furthermore, because PT has a high Curie temperature, Tc = 766 K, it is considered one of the most important end-component of the promising single crystal piezoelectric perovskites, such as PZT, PMN-PT, PZN-PT, and PMN-PIN(PbIn1/2Nb1/2O3)-PT. By employing LDA, GGA-PBE, GGA-PBEsol, GGA-AM05, we calculate static dielectric matrix, stiffness matrix and ion-clamped piezoelectric tensor at zero temperature. By comparing the DFT predictions with the available experimental results, we suggest more reliable functionals for the further studies, i.e. for the predictions of physical properties of PMN-PT, PZN-PT, and PMN-PIN-PT, which are being actively studied for the real applications.
In the present spin-polarized DFT calculations, the well-established Vienna ab initio simulation package (VASP) [7,8] was used. We used augmented projected augmented wave (PAW) pseudopotentials, and included the 5
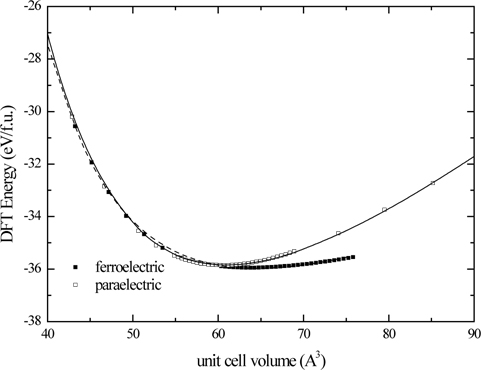
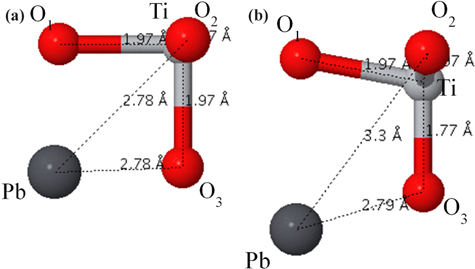
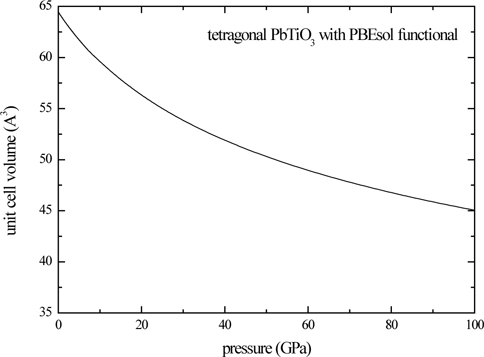
Energy-volume behaviors of the ferroelectric and paraelectric phases of PbTiO3 are shown in Fig. 1, where the PBEsol functional is used. Energetics of the system supports that lowest symmetry structure is the structure with the lowest energy. We can determine the minimum energy and the corresponding most stable structures given in Figs. 2(a) and 2(b). The cubic structure of PbTiO3 is completely described by the lattice constant
[Table 1.] Structural parameter of cubic paraelectric PbTiO3

Structural parameter of cubic paraelectric PbTiO3
The tetragonal structure of PbTiO3 is completely described by the lattice constant a, the ratio c/a, and by the displacement of ion their symmetric positions along the vertical z-direction (
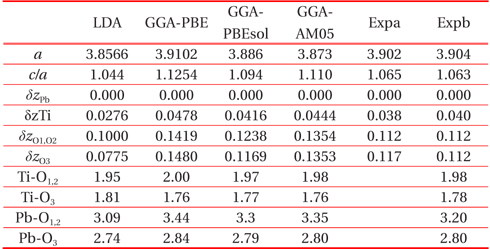
Structural parameters and bond lengths of tetragonal ferroelectric PbTiO3. The displacement of ion their symmetric positions along the vertical z-direction (δz) are given in terms of the lattice constant c.
Generally, at constant temperature, the bulk modulus is defined by:
Murnaghan [11] assumed that the bulk modulus is a linear function of pressure as
By integrating Eq. (1) with Eq. (2), we can get the following Murnaghan equation:
Also, we can also express the volume depending on the pressure:
Because in the present study we obtained the energy as a function of the volume, the following equation which connect the energy with volume is more useful:
The above equation is obtained by integrating Eq. (3) according to the relationship
Using the fully-relaxed structures, the piezoelectric tensor is determined by the density-functional perturbation theory (DFPT). In the present study, we calculated the piezoelectric tensor
The tetragonal phase PbTiO3 is polarized along the (001) axis. For a tetragonal lattice the three piezoelectric constants
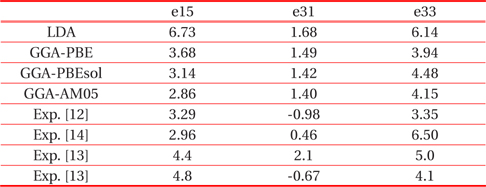
In Table 3 we summarized all the values calculated with the various functionals, also the available experimental data were given [12-14]. As shown in this table, the calculated results strongly depend on the choice of the exchange-correlation functional. Our
[Table 3.] Piezoelectric stress tensor elements (C/m2) of ferroelectric tetragonal PbTiO3.
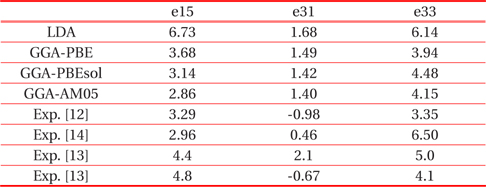
Piezoelectric stress tensor elements (C/m2) of ferroelectric tetragonal PbTiO3.
The pressure-dependency of the piezoelectric tensor is given in Table 4. Here, we calculate the piezoelectric constants for the structure optimized at fixed crystal volume, and estimate pressure by using Eq. (3). As shown in Table 4, the piezoelectric coefficient increases with pressure.

Predicted piezoelectric stress tensor elements (C/m2) of ferroelectric tetragonal PbTiO3. PBEsol functional is used for the exchange-correlation.
The structures of the PE and FE phases of PbTiO3 were investigated using the first principle quantum calculations. In the present study, under the density functional theory (DFT), various exchange-correlation functionals, such as LDA, GGA-PBE, GGA-PBEsol, GGA-AM05 were tested. All functionals predict the experimental results correctly to a certain degree, however the modified functionals for solid materials, i.e. GGA-PBEsol, GGA-AM05, yielded the structures and physical properties of PbTiO3 more reasonably than the conventional LDA and GGA-PBE functionals. In future studies, we will use GGA-PBEsol and GGA-AM05 functionals to investigate the structures and physical properties of the various piezoelectric materials such as PbMg1/3Nb2/3O3(PMN), PbMg1/3Nb2/3O3-PbTiO3 (PMN-PT) and PbIn1/2Nb 1/2O3- PbMg1/3Nb2/3O3-PbTiO3 (PIN-PMN-PT).