



Since the direct-gradient (DG) method uses the Shack-Hartmann wave front sensor (SH-WFS), based on the phase-conjugation principle, for atmospheric compensation in free-space optical (FSO) communication, it cannot effectively correct high-order aberrations. While the stochastic parallel gradient descent (SPGD) can compensate the distorted wave front, it requires more calculations, which is sometimes undesirable for an FSO system. A hybrid compensation (HC) method is proposed by properly using the DG method and SPGD algorithm to improve the performance of FSO communication. Simulations show that this method can well compensate wave-front aberrations and upgrade the coupling efficiency with few computations, preferable correction results, and rapid convergence rate.
Free-space optical (FSO) communication is an advanced technology to implement line-of-sight transmission of light signals. It transmits laser carrying signals through a free-space channel with high capacity, high bandwidth, and a flexible network [1]. FSO is one of the most promising alternative schemes for addressing the ‘last mile’ communication bottleneck in emerging broadband-access markets [2]. However, atmospheric disturbance can easily affect the laser beam. The refractive index of the atmosphere changes randomly because of variations in temperature, humidity, and wind speed in the atmosphere. This will lead to beam wandering, scattering, scintillation, and power fluctuations [3]. The phase and intensity of the laser are distorted, and the coupling efficiency decreases [4, 5]. Consequently the bit error rate (BER) of the communication system is degraded. This arouses the interest of researchers worldwide in studying phase correction, and effective methods are in high demand for FSO communication systems.
Adaptive optical (AO) systems have been successfully applied to FSO to compensate the distorted wave front [3-9]. Based on the phase-conjugation principle, traditionally there are two main branches. One in [6] is based on a wave-front sensor, such as the SH-WFS, to detect the local slope of the wave front and reconstruct the wave front in the Zernike or some other model. With a model, a deformable mirror (DM) can be controlled to construct a conjugated wave front, to offset the aberrations and obtain an approximately planar wave. In this method, the computational cost is very high for large numbers of subapertures in the sensor. Therefore the typically used sensors will fall short when high speed of detection and correction are needed, to implement fast adaptive optics in the FSO system. The other branch is the wave-front sensorless optimization method [3, 9], which aims to optimize the performance metrics of the received laser, such as Strehl ratio (SR), root mean square (RMS) and image sharpness functions, etc. The AO system searches for the suitable voltage to control the DM to optimize the performance metric. Many algorithms, such as simulated annealing (SA), hill climbing, and stochastic parallel gradient descent (SPGD) have been developed [5]. Among them, the SPGD algorithm is widely considered for its simple mechanism and rapid convergence, although hundreds of iterations are needed.
Recently, some new methods have been proposed. Reference [7] proposes a method to process Shack-Hartmann data by a focal-plane approach. This method is more favorable in noise propagation, compared to classical Shack-Hartmann, and senses more phase modes with fewer subapertures under a comparable computation burden. A phase-retrieval method is used instead of the wave-front-slope method to reconstruct the wave front in reference [8]. The method provides more accurate estimation of aberrations in nearly flat wave fronts. Interestingly, reference [10] proposes a combined approach involving SPGD and DM-model-based algorithms, to achieve similar correction results to those of SPGD with many fewer iterations. But in this method a SH-WFS is not effective, and both SPGD and DM-model-based algorithms need parameter settings that will increase the complexity of the method. In addition, a trust-region method has been proposed that is superior to both SA and SPGD algorithms, with respect to convergence rate for slowly changing wave-front aberrations, in reference [11].
Considering the rapidly changing atmospheric environment in an FSO system, we propose an HC scheme for wave-front corrections. This method combines the DG method [12] and SPGD algorithm to improve both the results of wave-front compensation and convergence rate.
This paper is organized as follows: In section II, the principles of the DG method and SPGD algorithm are briefly introduced and their deficiencies discussed, then we propose an HC scheme based on a suitable combination of the methods discussed above. In section III, computer simulations using MATLAB are carried out and the results are analyzed, to investigate the compensation capability of the HC scheme. Finally, we give our conclusion in section IV.
II. PROPOSED HYBRID COMPENSATION METHOD
The fundamental scheme of FSO communication is shown in Fig. 1. We adapt optical intensity modulation, and the data signals directly modulate the light source to generate optical signals. When the optical signals are transmitted to an atmospheric channel, they may suffer from atmospheric turbulence, and the receiver may receive optical signals with distorted wave fronts. Therefore, at the receiver we use an AO system to compensate for the aberrations of the distorted wave front. Then the optical signals with corrected wave fronts are coupled into the fiber and detected by the photodetector, to recover the original data signals.
As we know, a wave front distorted by atmospheric turbulence is commonly described by the Zernike polynomials [13], which are a set of polynomials defined on a unit circle. It is convenient to use polar coordinates, so that the polynomials are a product of angular functions and radial polynomials. The wave front is described as [14]
where (
To compensate a distorted wave front, the DG method is frequently used to detect and calculate a wave-front gradient matrix
where
For later use, we give a brief interpretation of Eq. (2). We suppose that the voltages applied to the actuators of the DM are linear, and let
where (
where (
On the other hand, the mean local gradient of the distorted wave front in the
where
Since this method directly calculates the optimal control voltage by the gradient of the wave front, without wave-front reconstruction, it can reduce the computational cost of the AO system. From Eq. (2) we can see that the influence function of DM is a key factor in compensation. To investigate the compensation capacity of the DM, we introduce the definition of compensation error as
where RMSo is the RMS value of the original distorted wave front, and RMSc is the RMS value of the corrected wave front. To test the general correction ability of the DM, the first 35 Zernike polynomials are taken as the targets for the correction, and all of their amplitudes are normalized. Here we consider a DM with 61 elements for the analysis. The compensation error of the 61-element DM for each Zernike order from 3 to 35 is shown in Fig. 2. From this figure, we can see that the compensation error increases with increasing Zernike order, which means the DG method is relatively incapable of correcting high-order aberrations.
For this reason, we introduce the SPGD algorithm for the sensorless wave-front compensation given in [3] to correct high-order aberrations. In this algorithm the object of optimization is a performance metric
where
and
For SPGD, given
Considering the effect of increasing convergence rate on the correction and the performance metric, we make use of the mature technologies of the DG and SPGD algorithms to propose an HC scheme based on a combination of the properties of these methods. For a distorted wave front, the DG method can compensate low-order aberrations without iteration, while the residual wave front consisting of a large proportion of high-order aberrations will be compensated by SPGD. In this way, the initial wave front corrected by SPGD is a less distorted wave front, with a smoother phase plane than the wave front of the inserted laser, which means much fewer iterations are needed to reach convergence. Moreover, our proposed HC scheme uses the SH-WFS to compensate the low-order aberrations, so that the accuracy requirement for the sensor is reduced, and we do not have to choose a SH-WFS with many subapertures. Large number of subapertures will divide the inserted laser power into many small parts, which causes difficulties in CCD detection. Furthermore, the computation pressure is relieved, since the size of
In this paper, we adapt a hybrid scheme by combining the mature schemes of the DG method and SPGD algorithm. The functional blocks are diagrammed in Fig. 3, in which the wave-front corrector is the DM shared by the Direct-Gradient Block and SPGD Block. The main process of this scheme is given as follows.
(1) When the light arrives, the Algorithm Selection Block identifies whether the inserted wave is the original, distorted wave or the residual wave, then selects the corresponding correction block. (2) If it is the original, distorted wave, the Direct-Gradient Block begins to detect the wave-front-gradient matrix G and calculates V of DM using Eq. (2). (3) The wave-front corrector generates a conjugated wave front to compensate the original wave front, and a residual wave is output. (4) The residual wave propagating back to the Algorithm Selection Block, is switched to the SPGD Block, and then iteratively corrected based on Eq. (8). With the SPGD algorithm, the wave front is iteratively corrected until the value of the performance metric J converges. (5) After correction, the optimized wave is coupled into the single-mode fiber and processed by the receiver. A diagram of this entire process is presented in Fig. 4.
For FSO, the coupling efficiency of the signals inserted into the fiber in the receiver has significant influence on system performance [15]. Thus in the SPGD block the performance metric
where
On the other hand, the BER of FSO communication links with on-off keying systems increases as RMS rises [17]. The relationship between RMS and SR is expressed as [16]
This means that the BER decreases with increasing SR. In other words, improvement of SR both increases coupling efficiency and reduces BER.
In the following section, by observing the SR of the system with our proposed compensation scheme, we present simulation results and analysis of wave-front compensation, to investigate the performance of our HC algorithm.
III. SIMULATION RESULTS AND ANALYSIS
In our simulations, for the Direct-Gradient Block we use the SH-WFS with an 8×8 subaperture array, in which the subapertures are not considered in every corner of the array shown in Fig. 5, to avoid detection difficulties in low light [6]. For the SPGD Block, the perturbations {
The distorted wave front that we introduce is the superposition of Zernike polynomials with coefficients
[TABLE 1.] Coefficients of Zernike polynomials

Coefficients of Zernike polynomials
Using this distorted-wave-front sample, we first simulate the DG method; after correction, the corresponding SR increases to 0.6958. The SRs of the iteratively corrected residual wave fronts are given in Fig. 7. From this figure, we can see that this method cannot further improve SR with increasing iterations, for high-order aberrations. Thus in our HC scheme the correction is carried out only once, to compensate the low-order aberrations with the DG algorithm and the high-order aberrations with the SPGD method.
Next we conduct the simulation of our HC scheme and compare its performance to that of the SPGD algorithm in correcting the original, distorted wave front. The improvements in SR for the HC and SPGD algorithms are presented in Fig. 8. We find that the HC scheme can converge much faster than the SPGD algorithm. In Fig. 8, when the SR is 0.8 the SPGD algorithm requires 144 iterations, but the HC scheme only needs 21. When the SR becomes 0.9, the number of iterations is about 370 by SPGD, while 110 by the HC scheme. Since the low-order aberrations have been corrected, the SR increases to 0.6958, so that further corrections implemented by the SPGD method need much fewer iterations.
Figure 9 shows the differences of the phase plane before and after correction. Figure 9(a) is the original, distorted wave front (SR=0.1668). It is obvious that it becomes flatter after correction by DG (SR=0.6958), as shown in Fig. 9(b), and it gets smooth after correction by the HC scheme (SR=0.9), as shown in Fig. 9(c). The range of the wave front narrows correspondingly.
Furthermore, we discuss the intensity characteristics of the laser beam to investigate the improvement of the coupling efficiency. The intensity
To verify the compensation effect of the HC scheme, besides the wave front discussed above, we introduce another seven wave fronts, simulated by Zernike polynomials with different maximum Zernike orders
From Fig. 11 we can see that the HC scheme is obviously superior to the SPGD algorithm, because it converges more rapidly than SPGD for every sample, especially for samples
Next we will perform a numerical analysis of the results. We define
[TABLE 2.] Correction results for different distorted wave fronts
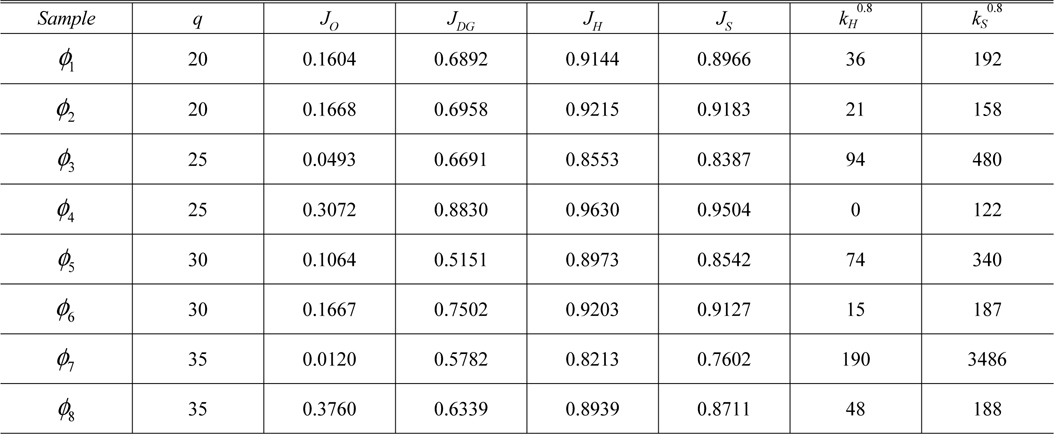
Correction results for different distorted wave fronts
To obtain convenient comparisons of correction results for different samples, we define the indice of the correction effect of the HC scheme as
For the samples enjoying better corrections by our HC scheme,
[TABLE 3.] Indices of correction effect and speed for the HC method

Indices of correction effect and speed for the HC method
As shown in Table 3, for samples of the same Zernike order, those with lower initial SR can realize higher
In summary, from simulations of different distorted wave fronts and the analysis of the results, we know that through a suitable combination of the DG method and the SPGD algorithm our HC scheme can achieve higher performance metrics than that of the DG method and convergent faster than the SPGD algorithm when low-order aberrations are compensated in advance by the DG method. After correction by the HC scheme, SR increases, so that the light intensity increases and more power is transmitted to the receiver, for higher coupling efficiency and improved communication quality.
In this paper we have proposed a hybrid-method HC scheme to compensate wave-front distortions resulting from the turbulent atmosphere in FSO communication. This scheme reduces the computational complexity of the compensation process and accelerates the convergence of the performance metric, to adapt to the real-time requirements of FSO communication. Based on the distorted wave fronts generated by Zernike polynomials, we compare the compensation performance of the SPGD algorithm, DG method, and our HC scheme by computer simulations. We find that with the SPGD-Block’s correction our HC scheme can achieve higher SR than the DG method, especially for wave fronts with higher Zernike orders. And the HC scheme can increase the correction speed of SPGD by increasing SR in the DG-Block, especially for severely distorted wave fronts, because high SR requires fewer iterations than low SR does. Our method can help an FSO system to improve coupling efficiency of the laser to the receiver and decrease BER.



























