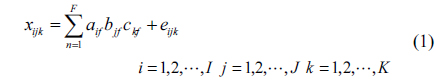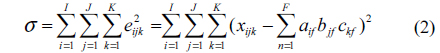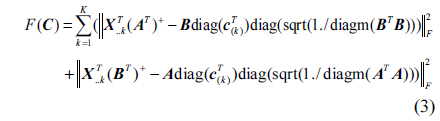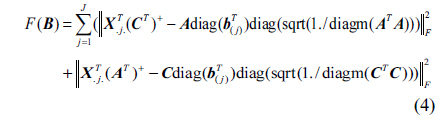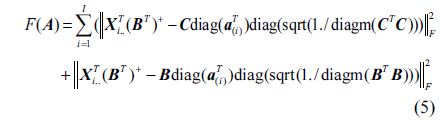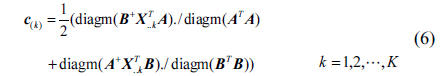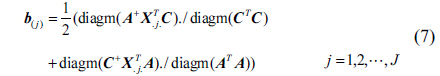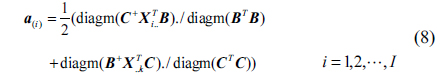Oil pollution seriously endangers the biological environment and human health. Due to the diversity of oils and the complexity of oil composition, it is of great significance to identify the oil contaminants. The 3-D fluorescence spectrum combined with a second order correction algorithm was adopted to measure an oil mixture with overlapped fluorescence spectra. The self-weighted alternating trilinear decomposition (SWATLD) is a kind of second order correction, which has developed rapidly in recent years. Micellar solutions of #0 diesel, #93 gasoline and ordinary kerosene in different concentrations were made up. The 3-D fluorescence spectra of the mixed oil solutions were measured by a FLS920 fluorescence spectrometer. The SWATLD algorithm was applied to decompose the spectrum data. The predict concentration and recovery rate obtained by the experiment show that the SWATLD algorithm has advantages of insensitivity to component number and high resolution for mixed oils.
Oil pollution seriously threatens the safety of human and ecological environment. Measuring oil pollutants has become an urgent problem [1]. Fluorescence detection has the advantages of good selectivity and high precision [2-5]. D. Patra applied three-dimensional fluorescence spectrometry to identify diesel with trace amounts of kerosene and gasoline, obtaining good result [6]. R. J. Kavanagh used synchronous fluorescence spectra to measure a variety of polycyclic aromatic hydrocarbons in water, and to successfully distinguish the type of polycyclic aromatic hydrocarbons [7]. Polycyclic aromatic hydrocarbons usually have stronger fluorescence properties [8-13], and the fluorescence spectra of oil pollutants are formed by the superposition of various aromatic hydrocarbon fluorescence spectra. It is relatively difficult to identify the type and determine the content of each component of oil mixture using chemical methods [14, 15]. The parallel factor (PARAFAC) analysis method is a kind of iterative three-dimensional matrix decomposition algorithm, which adopts the alternating least squares principle. It can quantitatively measure the specific components in the existence of interferents [16-18]. But only estimating the component number correctly can we get the accurate result [19, 20]. The self-weighted alternating trilinear decomposition (SWATLD) algorithm, which has been developed in recent years, is insensitive to component numbers, requires fewer iterations and has high stability [20-22]. Hu and Yin applied PARAFAC-alternative least squares (PARAFAC-ALSs) and SWATLD to measure Vancomycin and Cephalexin in human plasma, the experimental result showed that SWATLD algorithm had good effect on the determination of complex analysis of drugs in plasma [23]. Zhang and Wang determined Sulfonamides in synthetic samples and pharmaceutical tablets using SWATLD, showing that SWATLD algorithm can be easily performed and applied to solve second-order calibration problems quickly and accurately [24].
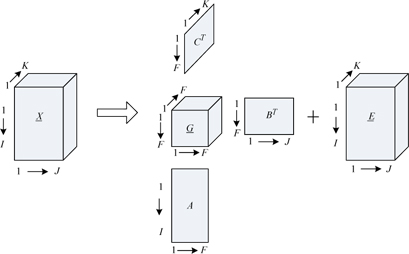
The PARAFAC model means a three-dimensional data matrix can be decomposed into three two-dimensional loading matrices
In Fig. 1, is a three-dimensional data matrix, with the sizes of
The PARAFAC model formula is expressed as:
The PARAFAC model has specific and actual chemical significance in three-dimensional fluorescence analysis. Scan the
The PARAFAC analysis algorithm takes advantage of the Alternating Least Square (ALS) method to decompose the three-dimensional matrix , aiming to minimize the sum of squared residuals [25]:
Where,
The PARAFAC algorithm has been widely used in the analysis of a three-dimensional fluorescence spectrum, while it is sensitive to component number, and the component number should be estimated accurately. Selecting the correct component number might get the good result. Therefore, a lot of improved PARAFAC algorithms are developed, among which, the SWATLD algorithm has the advantages of insensitivity to component number, fewer iterations, fast operation, good stability, etc.
The SWATLD algorithm is the improvement of the PARAFAC algorithm, and it optimizes the three objective functions which are close in internal relation but not completely equivalent. The functions are as follows:
Where, ||.|| represents the Frobenius matrix norm, ./ denotes array division.
After iterating the formula (3)~(5), we can obtain the following formula:
First, initialize
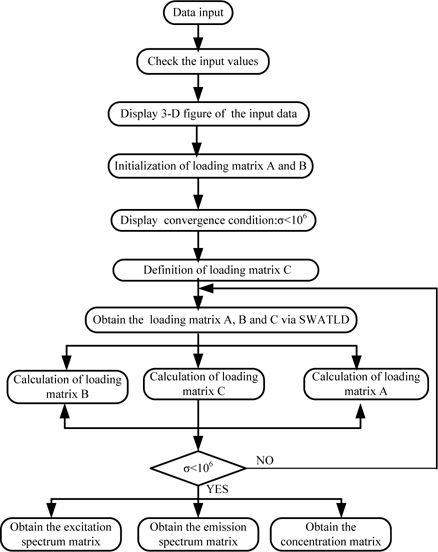
The process of the SWATLD algorithm is shown in Fig. 2.
III. EXPERIMENT AND DISCUSSION
3.1. Experiment Setting and Sample Preparation
The Edinburgh Instruments FLS920 full-function type fluorescence spectrometer is used as the fluorescence detector. The width between excitation and emission slit is 1.11 mm, spectral resolution 2 nm, integration time 0.1s, the excitation wavelength 250~400 nm, fluorescence emission wavelength 270~500 nm, each step length 5 nm. The starting emission wavelength lags the starting excitation wavelength 20 nm to avoid the interference of Rayleigh scattering. Measure the three-dimensional fluorescence spectrum of solutions twice and deduct the background spectrum of solvent to eliminate the effect of Raman scattering.
#97 gasoline and #0 diesel, and ordinary kerosene are the pollutants under test, sodium dodecyl sulfate (SDS) micellar solution is as the analysis of pure sample. The solubility of oil in the water is very low, which reduces the accuracy of the determination. As the solvent of oily substances, the SDS micellar solution can increase the fluorescence intensity of oil in the water, which is widely used in fluorometric analysis [26, 27].
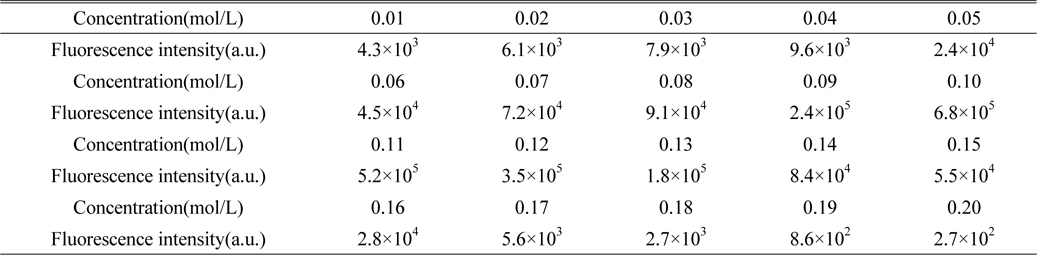
Firstly, prepare the SDS solution. Weigh the different quantities of SDS, and make 20 sets of SDS solution in deionized water, then add 0.05 g kerosene to each. Measure the fluorescence intensity of 20 sets of kerosene SDS solution, which is shown in Table 1. The results show that when the concentration of SDS is 0.1 mol/L, fluorescence intensity of the kerosene SDS solution is the largest, so we choose 0.1mol/L SDS solution as solvent.
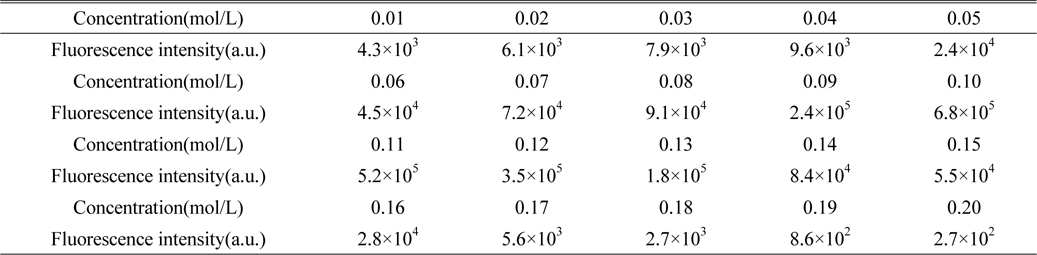
The concentration of SDS micellar solution and the fluorescence intensity of kerosene SDS micellar solution
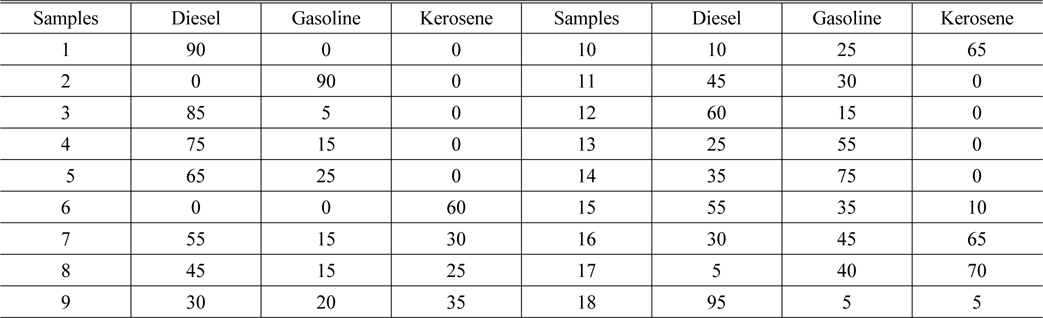
Prepare the 18 samples with different concentrations, and mark them. #1 ~ #10 are the calibration samples, and #11 ~ #18 are the prediction samples. The concentration in each sample is shown in Table 2.
[TABLE 2.] The oil concentration in each sample (mg/L)
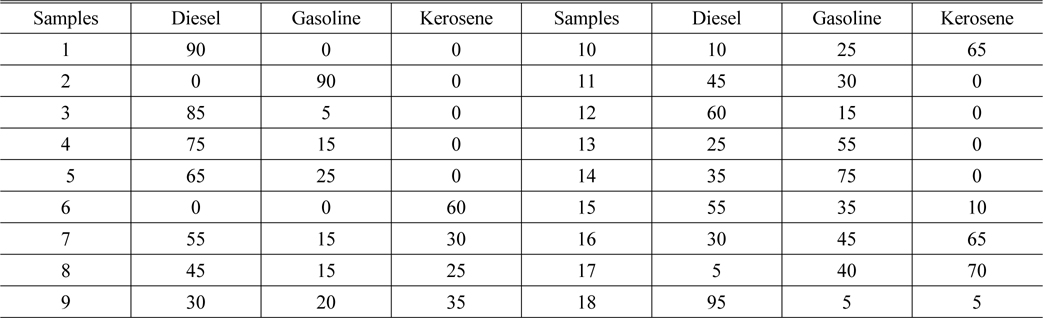
The oil concentration in each sample (mg/L)
3.2. Three-dimensional Fluorescence Spectra
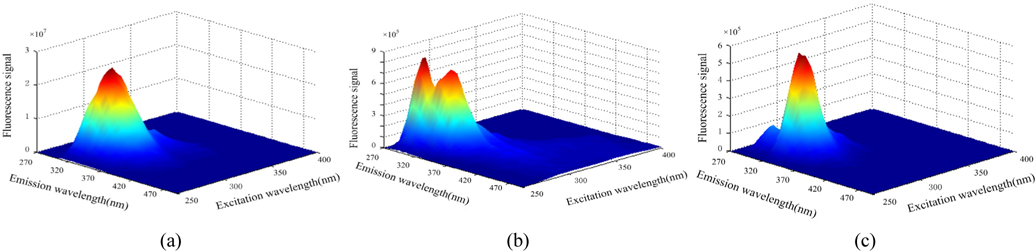
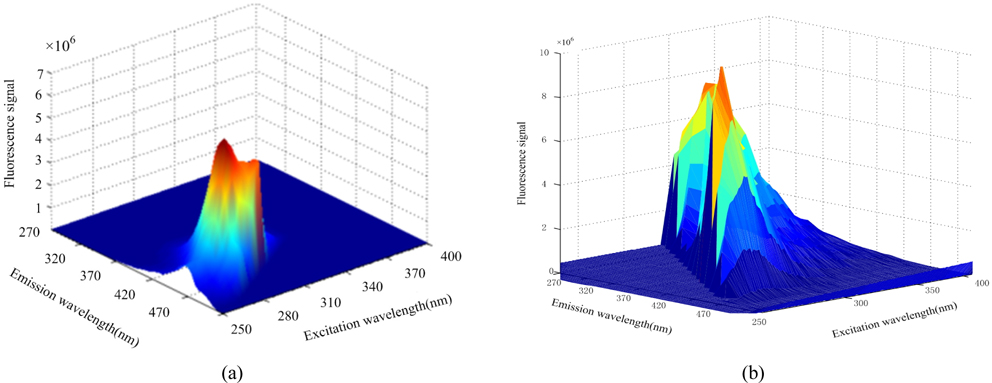
Figures 3(a), (b), (c) show the three-dimensional fluorescence spectra of diesel, gasoline and kerosene solutions respectively. Figure 5 shows the three-dimensional fluorescence spectra of two or three kinds of oil mixture solution. Although the fluorescence intensity of the oils are not identical, two or three kinds of mixed oil seriously overlap spectrally. It is difficult to separate the spectra and predict the concentration.
3.3. SWATLD to Mixed Solution of Diesel and Gasoline
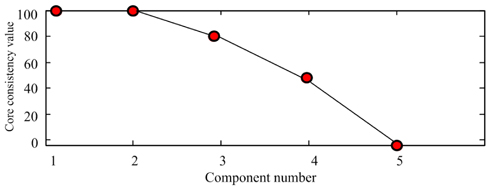
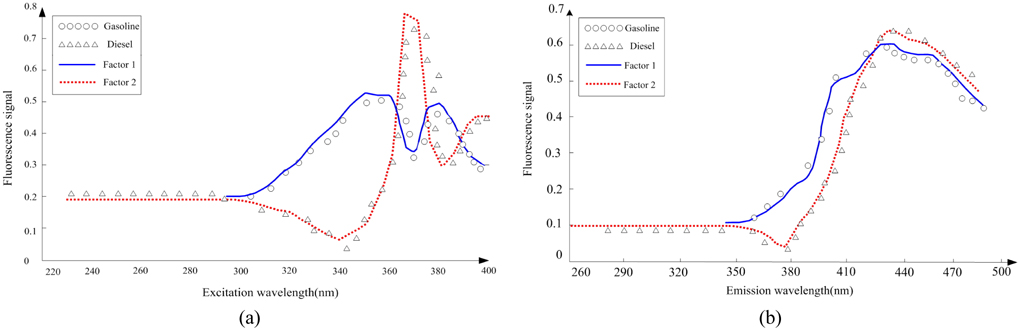
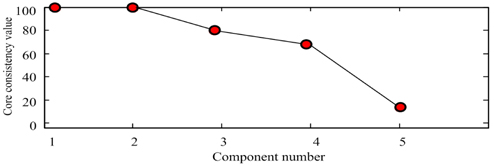
Scan the calibration samples #1 ~ #5 and prediction samples #11 ~ #14 to get the 3-dimensional data array , with the size of 9×37×21. Use the SWATLD algorithm to decompose . First, use the core consistent diagnosis method to estimate the component number. The core- consistency and the change of component number are shown in Fig. 5. When the component number is 1 or 2, the core-consistency is 100%. The component number increases, the core-consistency value reduces gradually, which deviates from the trilinear model, so choosing 2 as the component number is optimal. The excitation and emission spectra of the two omponents are shown in Fig. 6. The “OOOO” represents the actual spectrum of gasoline, and “ΔΔΔΔ” represents the actual spectrum of diesel. Component 1 and component 2 are obtained by the SWATLD algorithm. We can conclude that component 1 is gasoline , component 2 is diesel . The diesel and gasoline resolution spectra have high similarity and good repeatability to the actual spectra. The experimental result qualitatively shows that SWATLD has high resolution on the oil mixture.
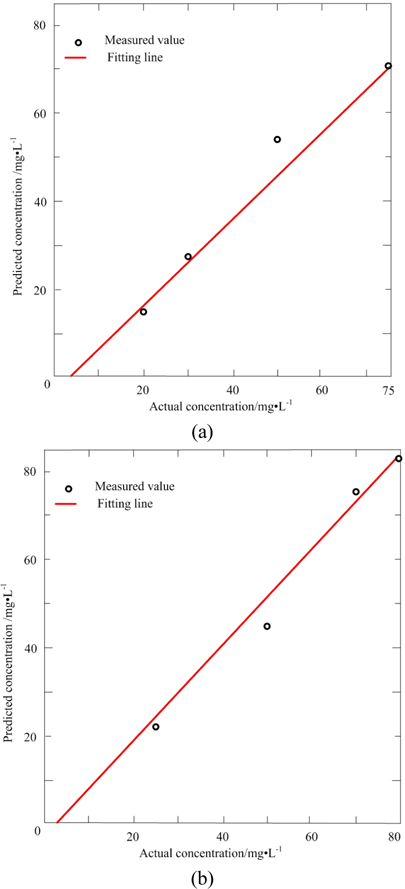
Table 3 lists the actual concentration of diesel and gasoline in the samples #11 ~ #14, the prediction concentration obtained by SWATLD and the recovery rate. Figure 7 shows the least square fitting lines between the actual concentration of the samples #11 ~ #14 and the prediction concentration obtained by SWATLD. The correlation coefficients are 0.9845(diesel), and 0.9926(gasoline). It quantitatively shows that SWATLD has high resolution on the oil mixture.
[TABLE 3.] The predicted concentration and recovery of diesel and gasoline obtained by SWATLD
The predicted concentration and recovery of diesel and gasoline obtained by SWATLD
3.4. SWATLD for Mixed Solution of Diesel, Gasoline and Kerosene
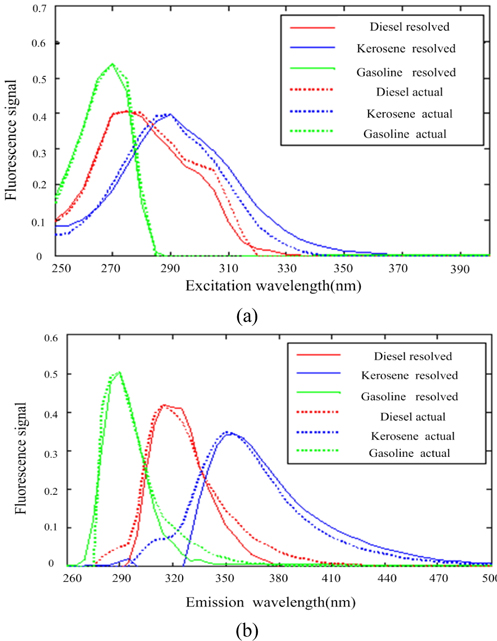
Scan the calibration samples #6 ~ #10 and prediction samples #15 ~ #18 to get the 3-dimensional data array , with the size of 9×37×21. Use the SWATLD algorithm to decompose . First, use the core consistent diagnosis method to estimate the number of components, as shown in Fig. 8. There is less difference in the core-consistency of 3 components and 4 components. As the SWATLD algorithm is not sensitive to component number, there is no need to estimate the component number accurately. We just need to make the component number greater than or equal to the actual component number to obtain the ideal results. Attempt to make the component number 3, and research the resolution of SWATLD on mixed oil. The excitation and emission spectra are shown in Fig. 9. The “diesel resolved”, “kerosene resolved” and “gasoline resolved” respectively represent the spectra of diesel, kerosene and gasoline obtained by the SWATLD algorithm. The “diesel actual”, “kerosene actual” and “gasoline actual” respectively represent the spectrum of actual diesel, kerosene and gasoline. We can conclude that the SWATLD algorithm has high resolution on 3 components oil mixture.
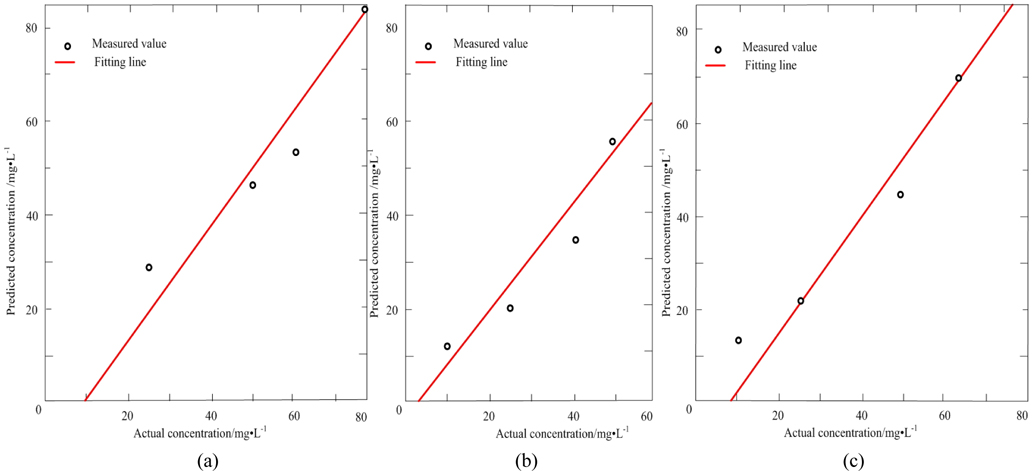
Table 4 lists the actual concentration of diesel, gasoline and kerosene in the samples #15 ~ #18, the prediction concentration obtained by SWATLD and the recovery rate. Figure 10 shows the least square fitting lines between the actual concentration and the prediction concentration obtained by SWATLD. The correlation coefficients are 0.9034(diesel), 0.9252(gasoline), 0.9643(kerosene). It is shown that SWATLD has high resolution on three or more kinds mixed oil.
The predicted concentration and recovery of diesel, gasoline and kerosene obtained by SWATLD
Aimed at the problem of oil pollutants that are not easy to distinguish, a second order correction method was put forward. As the SWATLD algorithm is insensitive to factor numbers, there is no need to estimate the component number accurately. We just need to make the component number greater than or equal to the actual component numbers to obtain the ideal results. First, the diesel, gasoline and kerosene mixed solution was made up as calibration samples and prediction samples. Second, the FLS920 fluorescence spectrometer was used to measure the three-dimensional fluorescence spectra of the samples. The mixed solution spectra overlapped seriously, and it was difficult to distinguish each specific oil. And then the SWATLD algorithm was adopted to decompose the mixed oil. The decomposed spectra had high similarity with the measured spectra of each kind of oil. In addition, the concentration recovery rate was high. The experimental results show that the SWATLD algorithm has good effect on the separation of oil mixtures with overlapped spectra.
three-dimensional data matrix residual matrix A, B, C two-dimensional loading matrix xijk the ijkth element of aif, bif, ckf the ifth, jfth and kfth elements of loading matrix A, B, C eijk the ijkth element of the three-dimensional residual matrix σ the sum of squared residuals F the component number
