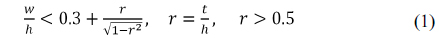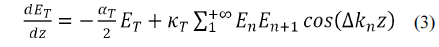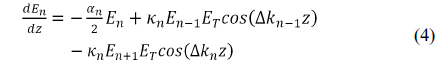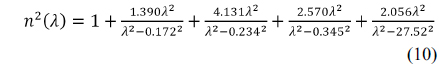Terahertz (THz) generation by a GaP ridge waveguide with a collinear modal phase-matching scheme based on cascaded difference frequency generation (DFG) processes is theoretically analyzed. The cascaded Stokes interaction processes and the cascaded anti-Stokes interaction processes are investigated from coupled wave equations. THz intensities and quantum conversion efficiency are calculated. Compared with non-cascaded DFG processes, THz intensities from 11-order cascaded DFG processes are increased to 5.48. The quantum conversion efficiency of 177.9% in cascaded processes can be realized, exceeding the Manley-Rowe limit.
The terahertz (THz) radiation, which is generally referred to as the frequency from 0.1 to 10 THz, has recently drawn much attention due to its tremendous potential applications, such as imaging, material detection, environmental monitoring, communication, astronomy and national defense security [1-4]. For such applications, a high-power, widely tunable, and compact source of THz-wave is required. Due to the interest in exploiting this region there have been many schemes proposed on source technologies over the last twenty years or so [5-10]. Among many electronic and optical methods for the coherent THz-wave generation, difference frequency generation (DFG) [11-14] is of importance because it offers the advantages of relative compactness, narrow linewidth, wide tuning range, high-power output and room-temperature working environment. In DFG, two optical pump beams, with their frequencies separated by a few THz, interact through a χ(2) process to generate a THz beam. Unfortunately, the quantum conversion efficiency of the DFG is extremely low as the THz-wave is intensely absorbed by the nonlinear optical crystal. To improve the low quantum conversion efficiency and overcome the Manley-Rowe limit, cascaded DFG in which more than one THz photon is generated from the depletion of a single pump photon is a promising method. Theoretical descriptions and experimental demonstrations of an enhancement output of THz wave via cascaded DFG processes have been reported recently. Liu
The conversion efficiency of the cascaded DFG process is primarily determined by the effective interaction length and the absorption in the nonlinear optical crystal at THz frequencies. Usually, collinear phase matching is a preferred scheme to maximize the effective interaction length. THz wave generations by GaP rib waveguide via collinear modal phase-matched DFG have been observed [18]. While GaP has a large optical nonlinearity for THz DFG (50 pm/V at 1.55 μm [19]), its absorption coefficient in the THz range is relative large and increases rapidly with increasing frequency. Despite the fact that the THz wave is intensely absorbed by the optical crystal in collinear phase matching configuration, co-propagating the THz wave with the pump and signal waves in the same direction can achieve long- range amplification of the THz wave in a nonlinear crystal until pump depletion [20].
In this paper, we present the theoretical analysis of THz generation by GaP ridge waveguide with a collinear modal phase-matching scheme based on cascaded DFG processes. We investigate the cascaded Stokes interaction processes and the cascaded anti-Stokes interaction processes. THz intensities and quantum conversion efficiency are calculated from coupled wave equations.
Figure 1 shows a schematic diagram of THz wave generation by collinear modal phase-matching cascaded DFG. TM-like guided THz wave in the GaP ridge waveguide was generated through type-I phase matching when the electric fields of both pump and signal waves are along [110]. THz wave (
THz wave is guided by a GaP ridge waveguide with dimensions
The collinear modal phase-matching condition in the ridge waveguide is expressed as
where
The coupled wave equations of cascaded DFG can be derived from common nonlinear optical three-wave interaction equations, shown as
where
The theoretical values of refractive index are calculated using a wavelength-independent Sellmeier equation for GaP in the IR [23] and THz [24] range, respectively. The Sellmeier equation for GaP of Madarasz
The Sellmeier equation for GaP in the THz range [24] can be written as
where
Here, in simulating the cascaded DFG dynamics, pump wave
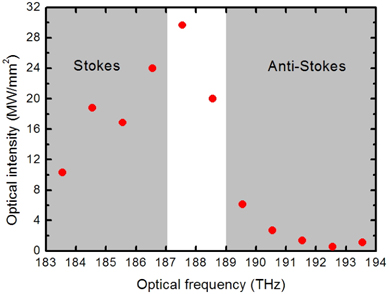
As the Stokes processes generate THz photons and the anti-Stokes processes consume THz photons, THz intensities depend on the Stokes processes and the anti-Stokes processes. Figure 4 shows the maximum intensities of the optical waves during the cascaded Stokes processes and anti-Stokes processes. In this figure we assume that the optical waves at interval of 1 THz with frequencies from 183.55 to 193.55 THz interact in the Stokes and anti-Stokes processes. The initial pump and signal waves are 188.55 and 187.55 THz, respectively, with a power density of 20 MW/mm2. From the figure we find that the power densities of optical waves in the Stokes processes is higher than that of optical waves in the anti-Stokes processes, which indicates that the Stokes processes are stronger than the anti-Stokes processes. In the cascaded Stokes processes,
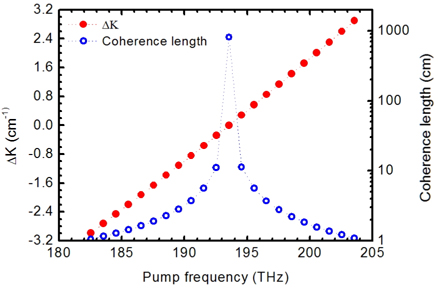
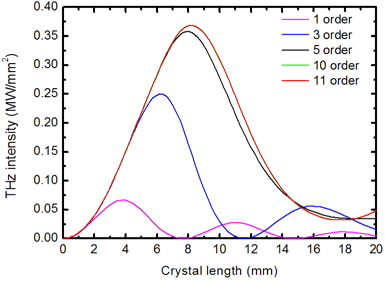
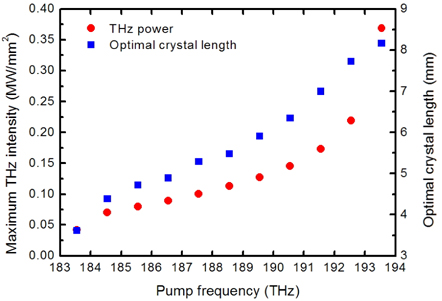
Figure 5 shows the relationship between the maximum THz intensities and the pump wave frequencies. In this figure we assume that the optical waves at interval of 1 THz with frequencies from 183.55 to 193.55 THz interact in the cascaded Stokes and anti-Stokes processes. The frequency of the pump wave is 1 THz larger than that of the signal wave. Both the pump and signal intensities are 20 MW/mm2. From the figure we find that THz intensities are higher as the pump frequencies locate in the high-frequency area. The high THz intensities originate from the interaction of the high-order Stokes processes as the pump frequencies locate in the high-frequency area, which indicates that the Stokes processes are stronger than the anti-Stokes processes. As the pump frequency equals 193.55 THz, THz wave with a maximum intensity of 0.3686 MW/mm2 can be obtained. In the high-frequency area where high-order Stokes processes interact, optimal crystal lengths are longer considering cascading, which is consistent with the principle of cascaded nonlinear processes.
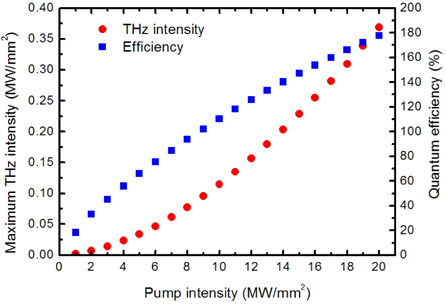
Pump intensity is directly related to the quantum conversion efficiency in a cascaded DFG processes. The maximum THz intensity and quantum conversion efficiency are calculated when the original pump intensities are changed from 1 MW/mm2 to 20 MW/mm2, as shown in Fig. 6. In the calculations, pump wave and signal wave are supposed to be 193.55 and 192.55 THz, respectively. Fig. 6 demonstrates that the maximum THz intensity and quantum conversion efficiency significantly increase with the pump intensity. THz wave with a maximum intensity of 0.3686 MW/mm2 can be generated as pump intensity equals to 20 MW/mm2, corresponding to the quantum conversion efficiency of 177.9%. The quantum conversion efficiency of 177.9% in cascaded processes exceeds the Manley-Rowe limit.
THz generation with the frequency of 1 THz with a collinear modal phase-matching scheme based on cascaded DFG processes is theoretically analyzed above. As for THz waves with frequencies lower than 1 THz, THz generation can be effectively enhanced based on cascaded DFG processes if the collinear modal phase-matching scheme is satisfied. As for THz waves with frequencies larger than several THz, the output of the THz wave is seriously affected by the absorption by the GaP crystal as the absorption coefficients of THz wave in GaP crystal rapidly increase with the increase of frequency.
THz generation by GaP ridge waveguide with a collinear modal phase-matching scheme based on cascaded DFG processes is theoretically analyzed. The cascaded DFG processes comprise the Stokes interaction processes and the cascaded anti-Stokes interaction processes. The calculation results indicate that the Stokes processes are stronger than the anti-Stokes processes. Compared with non-cascaded DFG processes, THz intensities from 11-order cascaded DFG processes are increased to 5.48. THz wave with a maximum intensity of 0.3686 MW/mm2 can be generated as pump intensity is 20 MW/mm2, corresponding to the quantum conversion efficiency of 177.9%. The quantum conversion efficiency of 177.9% exceeds the Manley-Rowe limit, providing us an efficient way to enhance the output of THz waves.
![Schematic diagram of the cascaded DFG to generate THz radiation by GaP ridge waveguide. DFG with Type-I phase matching condition, the electric field vectors of pump and signal wave Ep and Es are along [110], and that of THz wave ET is along [001] .](http://oak.go.kr/repository/journal/20733/E1OSAB_2016_v20n1_169_f001.jpg)