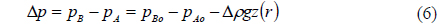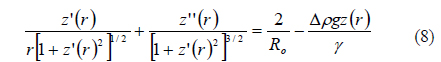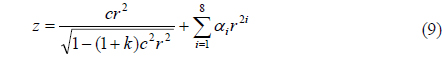The liquid lens is a novel optical element which features dynamic adjustment of the lens refractive index or its surface shape to change the focal length. The liquid lens has the advantage of being able to change focal length without mechanically moving the lens, which can provide considerable power savings and can eliminate wear associated with moving parts [1], so it is widely used in a large variety of application areas, such as mobile phones [2], surgical instruments [3], miniature cameras [4], and so on. The double-liquid lens [4-7] based on the electrowetting effect is highly regarded because of its outstanding performance [7].

Currently in most of the studies about the double-liquid lens, the two liquids’ densities are the same to ensure that the liquid interface is a spherical surface [8, 9]. The density difference of two liquids can affect the interface shape and the final focal length of the system [10]. In this paper, the effect of the two liquids’ density difference on the interface shape is discussed in detail, and the imaging quality of the double-liquid lens with an aspheric interface is analyzed with Zemax optical design software.

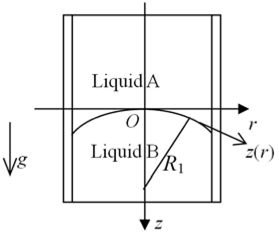
Figure 1 is the schematic diagram of a double-liquid lens. According to the Laplace equation [11], at any point on the interface of two liquids,

where Δp is the pressure difference between the top and the bottom of the interface at any point, γ is the interface tension between Liquid A and Liquid B, R₁ and R₂ are the curvature radii of any point on the interface in the orthogonal direction.

In accordance with the coordinate system of Zemax software, here choose the coordinate system shown in Fig. 1; the origin of the coordinate is at the interface apex, the z axis is the direction of the optical axis. In this paper, both radii can be expressed by the function z(r):

where R₁ is the radius of curvature in the plane of Fig. 1 and R₂ is the radius of curvature in the plane perpendicular to Fig. 1.

The pressures at each point of the interface can be expressed as

where p_Ao and p_Bo are the pressures of Liquid A and Liquid B at the origin, respectively, ρ_A and ρ_B are the densities of Liquid A and Liquid B, respectively, g is the acceleration of gravity, the gravitational direction is shown in Fig. 1. So

where Δρ = ρ_A-ρ_B, is the liquid density difference. Because the radius of the interface vertex (R_o) in any direction is the same, the pressure difference at the origin (p_Bo - p_Ao) can be described by the Laplace equation:

Combine Eqs. (1)~(3), (6) and (7), and a differential equation, which determines the shape of the liquid interface, can be obtained:

Eq. (8) is the relationship between the liquid density difference and the interface shape of a double-liquid lens. The interface shape is completely spherical when the density difference of the two liquids is zero [7].

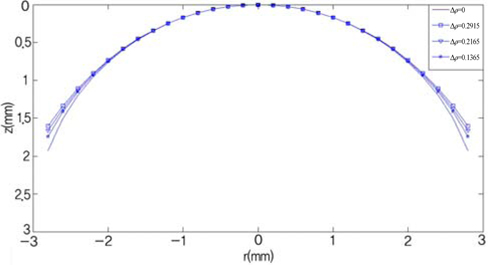
In order to analyze the effect of the two liquids’ density difference on the interface shape in detail, two liquids with different densities are chosen, for example, CH₂Cl₂ as “Liquid A” (insulating liquid, the density ρ_A is 1.3255 g/cm³) and NaCl solution as “Liquid B” (conducting liquid). When the concentration of NaCl solution is different, its density ρ_B can be slightly different (Table 1). And the liquid density differences (Δρ) of the NaCl solution and the CH₂Cl₂ are shown in Table 1.

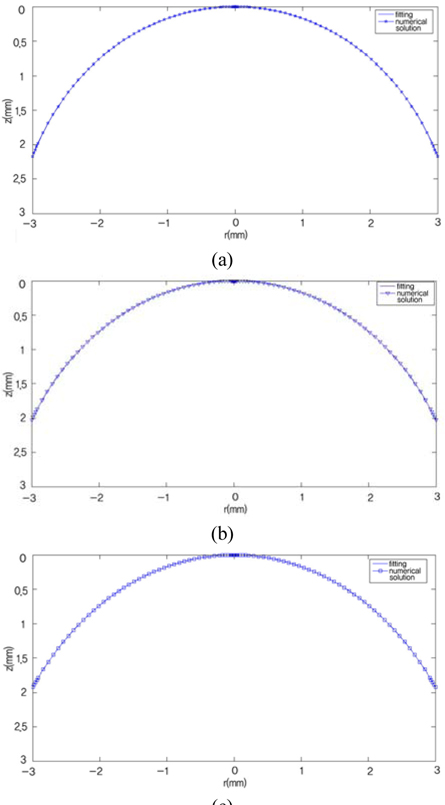
By using these values of Δρ, the related constants and by solving Eq. (8) numerically, the interface shapes of double-liquid lenses with different liquid density differences are obtained and shown in Fig. 2. The spherical interface curve is depicted by a solid line in Fig. 2 when Δρ=0 for comparison. The other interface shape curves of a double-liquid lens with Δρ≠0 deviate from the spherical interface curve. It is found that the density difference of two liquids can cause the interface to be an aspheric surface, and when the liquid density difference is larger, the interface asphericity is more obvious.

The aspheric interface shapes of double-liquid lenses are fitted with a rotationally symmetric polynomial aspheric surface (even asphere), which in Zemax is given by

where c is the curvature (the reciprocal of the radius), k is the conic constant and α_i is the aspheric coefficient, of which only the front four items are used. The aspheric coefficients of interface shapes of double-liquid lenses with different liquid density differences are shown in Table 2. The fitting interface shape curves, which are depicted by solid lines in Fig. 3, are consistent with the shape curves of numerical solutions depicted by stars (Δρ=0.1365), inverted triangles (Δρ=0.2165) and squares (Δρ=0.2915). Therefore, the expression of aspheric interface shape of double-liquid lenses can be obtained and used in Zemax.

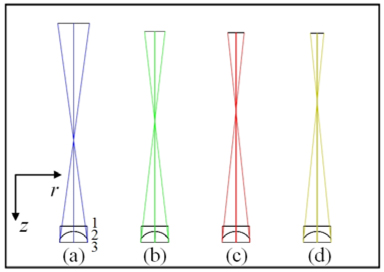
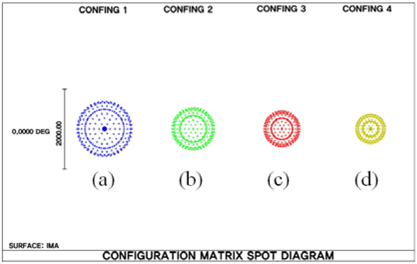
With the aspheric coefficients shown in Table 2, the double-liquid lenses with aspheric interface are designed with Zemax. For comparison, the double-liquid lens with spherical interface is designed, too.

The schematic plots of double-liquid lenses with (a) Δρ =0, (b) Δρ=0.1365, (c) Δρ=0.2165 and (d) Δρ=0.2915 are shown in Fig. 4. From top to bottom, the first surface to the second surface represents CH₂Cl₂, the second surface to the third surface represents NaCl solution. The focal length of the double-liquid lens is negative. When the image surface is set as a Gaussian image surface, the direction of the converging rays is opposite to the optical axis. From the spot diagram on the image surface shown in Fig. 5, it is found that with the increase of liquid density difference, i.e. the increase of the asphericity, the size of the spot decreases and the image quality is improved gradually.

Due to the gravity effect, in the section of imaging analysis with Zemax, the pupil diameter of the double-liquid lens is limited to be 5 mm [9]. When the diameter of the double-liquid lens is greater than 5 mm, the gravity effect needs to be considered. In this paper, the work is mainly focused on the discussion of the stable static interface shape of double-liquid lens; the analysis of interface shape is completed without consideration of liquid internal pressure changes and under no applied voltage on the conducting liquid. The effect of internal pressure and external applied voltage on the interface shape of the double-liquid lens will be analyzed in our further research.

On the other hand, in order to ensure the symmetry, the price of obtaining a stable aspheric interface in the double-liquid lens is that it is necessary to fix the position of the lens and not to move it at will. In the future, the liquid lens with aspheric interface will be used in the human eye model, as a confirmed zooming system, which can be applied to provide the intuitive presentation of human eye zooming characteristics. We are conducting the research work of the human eye model containing a liquid lens. The liquid lens with aspheric interface may be applied in the other fixed presentation models like the human eye system.

The development of the aspheric lens is limited by manufacturing costs. However, by the above analysis and fitting of interface shape of the double-liquid lens, it is found that the aspheric surface of the double-liquid lens can be obtained by the liquid density difference easily. And the image quality of the double-liquid lens with aspheric interface is improved obviously. Therefore, the result provides a new selection for the related further research and a wider application field for the liquid lens.