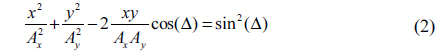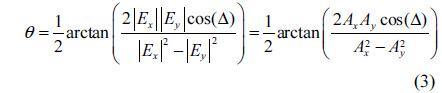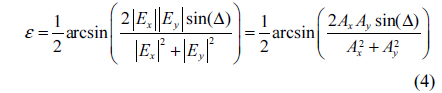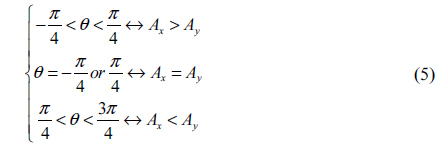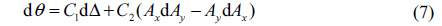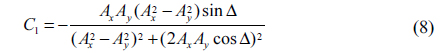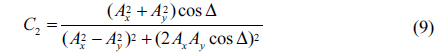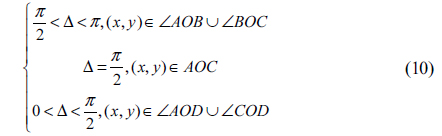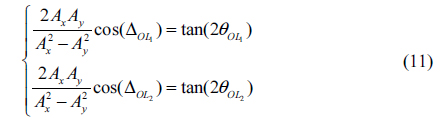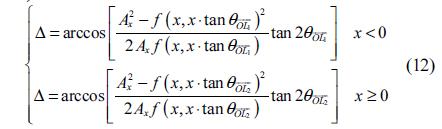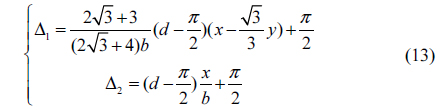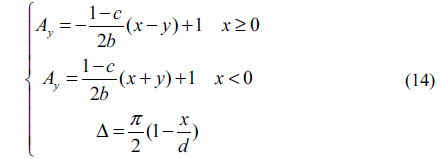Since Nye and Berry first found dislocations in optical fields in 1974 [1], singular optics have been a subject of interest. The diverse singular patterns provide rich information about the fine structure of light. While phase singularities (wave dislocations, or optical vortices) are frequently encountered in the interference of scalar waves, they resolve into polarization singularities (PSs) when the vector nature of light is retained [2-6]. PSs include C-points (points where the light is circularly polarized) and L-lines (lines where the light is linearly polarized) [2]. These PSs determine the distribution of polarization ellipses around them, such as how in nonparaxial fields the major axes (minor axes) of polarization ellipses surrounding C-points are shown to form Möbius strips [3-5], while in paraxial fields polarization ellipses around C-points produce interesting structures named Lemon, Mon-Star, and Star [2, 6]. Experiments have been successful in generating PSs [7-13], but generation of PSs with a desired shape or structure, especially generation of a Mon-Star, is still a challenge. This is because the distributions of amplitude and phase around C-points are complex and have not been developed clearly.

In this paper, a Cartesian coordinate system with origin at the C-point is established. Then, four curves where the azimuthal angles of polarization ellipses are 0°, 45°, 90°, and 135° respectively are used to determine the distribution functions of amplitude and phase around C-points; these distributions include the Lemon, Mon-Star, and Star. Discussion of these distributions illustrates the difficulty of generating a Mon-Star in experiments. The probabilities of transformation of these three PSs are also discussed. According to the distributions of amplitude and phase, we give suitable functions and simulate several particularly shaped PSs. With the development of modulation techniques for amplitude and phase, it is clear that the work in this paper is helpful for generating arbitrarily shaped C-points in experiments.

To analyze the distributions of (or constraints for) amplitude and phase around a C-point, we need to write the electromagnetic wave in term of the Jones matrix:

where A_x and A_y denote the amplitudes of E_x and E_y respectively, while α_x and α_y denote the corresponding phases. With appropriate calculation, the trajectory equation of the end of vector can be written as

where Δ=α_y−α_x is the phase difference between E_x and E_y. Eq. (2) denotes an internally tangent ellipse in a rectangle of dimensions 2A_x×2A_y, as shown in Fig. 1. The behavior of the ellipse depends on A_x, A_y, and Δ, so we analyze the phase difference Δ instead of the phases α_x and α_y. The azimuthal angle θ and the ellipticity ε are two important parameters of the polarization ellipse [14]:

where the azimuthal angle θ is defined as the angle between the major axis of the polarization ellipse and the +x axis

Combining Eqs. (2) and (3) and considering Fig. 1, we obtain the following relationship:

where ↔ is the symbol for “necessary and sufficient”. Eq. (5) is a very important conclusion to determine the distributions of the amplitude and phase difference, as follows.

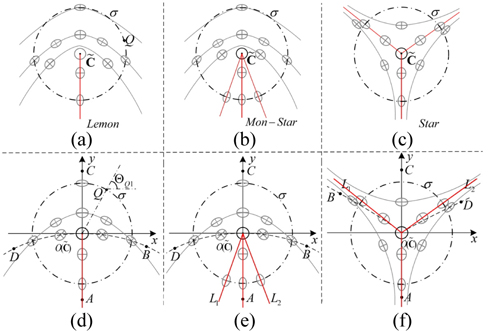
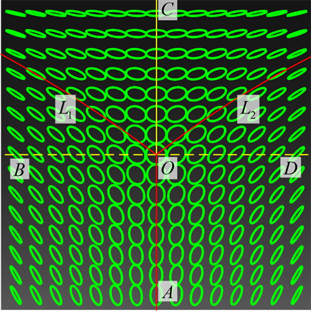
It is well known that there are three typical kinds of polarization singularities: Lemon, Mon-Star, and Star, shown in Figs. 2(a), (b), and (c) respectively [2, 6]. In Fig. 2 the gray ellipses surrounding C-point present the polarization states of the fields. The gray solid curves are the envelopes of the azimuthal angles of polarization ellipses. Among these envelopes, there are some rays (the red rays in Figs. 2(a)~(c)) emanating from the C-points . The azimuthal angles of polarization ellipses on these rays equal the angle between the ray and the +x axis. Obviously there is one ray emanating from the Lemon, while three emanate from the Mon-Star and Star [2, 15, 16]. To identify the type of PS, a very small circle σ with center at the C-point is drawn. Assuming that the azimuthal angle of a polarization ellipse at point Q on σ is ϕ, the value of ϕ varies as point Q moves along σ anticlockwise. Considering the total change in ϕ over σ, we have Δϕ =+π for Lemon or Mon-Star and Δϕ=−π for Star. Dividing Δϕ by 2π, we get the winding number I = +1/2 for Lemon or Mon-Star and I = −1/2 for Star. The function for the winding number is given as [17]. The winding number and number of rays jointly determine the type of the PS.

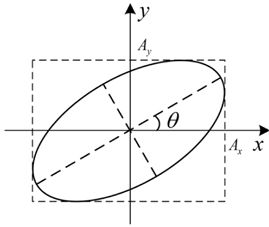
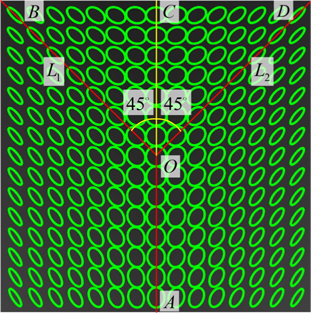
Next a Cartesian coordinate system is established with origin O at the C-point and -y axis coinciding with one of the rays, as shown in Figs. 2(d)~(f). Thus the -y axis is where the azimuthal angles of polarization ellipses are 90°, and is marked as . Then three other curves where the azimuthal angles are 0°, 45°, and 135° are drawn out and marked as , and respectively, when they are rays. Because of the different distributions of polarization ellipses, rays and are to the right and left, respectively, of AOC in Figs. 2(d) and (e), while they swap positions in Fig. 2(f). We mark the other two rays in Figs. 2(b) and (c) as and , respectively, as shown in Figs. 2(e) and (f). The field is divided into four regions, denoted by ∠AOB, ∠BOD, ∠COD, and ∠AOD. Establishing the Cartesian coordinate system and the four curves makes for concise analysis of the amplitude and phase of a PS, will be demonstrated as follows.

Now considering the amplitude distribution of the Lemon in Fig. 2(d), we find the curve BOD to be a dividing curve, upon which azimuthal angles of ellipses change within the range of −π/4<θ<π/4, and under which the range is π/4<θ<3π/4, and at which the azimuthal angles are π/4 or 3π/4. According to Eq. (5), the amplitude distribution of the Lemon is given as:

Eq. (6) is the distribution function of amplitude around the Lemon. Now we analyze the distribution of phase around the Lemon. We assume that the field around the C-point is left-hand-polarized, namely 0<Δ<π. As shown in Fig. 2(d), the azimuthal angle on ray is , while on ray . Substituting and for θ in Eq. (3), we obtain Calculating the derivative of Eq. (3),

where

Taking a point that is infinitely close to and on the right of , then the difference in θ is positive, namely dθ>0. Substituting A_x < A_y, dA_x > dA_y, and Δ=π/2 into Eqs. (7)~(9), we have dΔ>0. Using this analysis method, the distribution of the phase difference is given as

Eq. (10) means the curve AOC is also a dividing curve for the phase difference, while the curve BOC is the dividing curve for the amplitude. These two curves make the amplitude and phase around a C-point simple and clear, which is why we establish the Cartesian coordinate system and need the help of the four rays , , , and .

According to the structures shown in Fig. 2, the ellipses surrounding Lemon and Mon-Star have the same tendency, apart from the number of rays (one for Lemon and three for Mon-Star). In other words, Mon-Star can be regarded as special Lemon. So the amplitude and phase of Mon-Star must be bound by Eqs. (6) and (10), respectively. On the other hand, there exist two other rays and in the field of the Mon-Star, as shown in Fig. 2(e). Naming the azimuthal angles of ellipses on and as and respectively, and implementing the simple transform of Eq. (3), we have

This formula is a function of amplitude and phase simultaneously, which means the amplitude and phase on rays and should follow Eq. (11), while being restricted by Eqs. (6) and (10). It seems complex to construct amplitude and phase that satisfy Eqs. (6), (10), and (11) simultaneously. However, when the amplitude is set according to Eq. (6), the phase can be determined according to Eqs. (10) and (11). Similarly, a set phase can used to determine the amplitude according to Eqs. (6) and (11).

Compared to Lemon and Mon-Star, the Star has a different elliptic tendency. However, the analysis method used above is also suitable for acquiring the distributions of amplitude and phase around the Star. Compared to those for Lemon, the amplitude and phase of Star have the same expressions as Eqs. (6) and (10), respectively, but we emphasize that because of the opposite spatial positions of and in Figs. 2(d) and (f), the distribution of phase for Star differs from that for Lemon. As for Mon-star, there are also two other rays ( and ) in the field of Star, so the amplitude and phase of Star are likewise restricted by Eq. (11).

Now we see that the analyses of amplitude and phase for Lemon, Mon-Star, and Star become very concise. In addition, these distributions of the three PSs can be expressed by the same forms (Eqs. (6), (10) and (11)). These are the benefits of establishing the Cartesian coordinate system and the four rays , , , and .

Developing distribution functions of amplitudes and phases around C-points ultimately benefits the generation of PSs. According to the constraints, constructing amplitude and phase is a crucial step in generating the desired PSs. Constructing amplitude and phase functions following Eqs. (6) and (10) for Lemon is easy. Here we try to give expressions used to generate Mon-Star and Star when and coincide with −y and +y respectively. For convenience but without loss of generality, we assume that t he component E_x is a plane wave, i.e. A_x and α_x are constants. Assuming that we know the amplitude according to Eq. (6), denoted as A_y = f(x, y), the equation for is Then substituting A_y, , and into Eq. (11),

Eq. (12) is not the only expression that makes the amplitude and phase obey Eqs. (6), (10) and (11) simultaneously.

In section II we obtained distributions of amplitude and phase around the C-points Lemon, Mon-Star, and Star. We note that the work of [7] is a theoretical description of optical beams carrying isolated polarization singularity C-points. The PSs are formed by the superposition of a circularly polarized mode carrying an optical vortex and a fundamental Gaussian mode in the opposite state of polarization. By varying two parameters, C-points including asymmetric Lemon, Mon-Star, and Star can be generated. Compared to [7], in this paper the electromagnetic waves are written in the more general terms of the Jones matrix, i.e. PSs are formed by the superposition of two linearly polarized modes that are orthogonal to each other. We analyze distributions of the amplitude and phase differences of the two polarized modes. According to the analyses, all three kinds of PSs can be generated (as shown in section IV). Moreover, the positions of the curves where the azimuthal angles of polarization ellipses are 0°, 45°, and 135° can be controlled.

For the Lemon, the amplitude must follow Eq. (6), while the phase must follow Eq. (10). These two formulas are independent constraints on the amplitude and phase, respectively. Thus there is a high probability to obtain amplitude and phase obeying Eqs. (6) and (10), which means generation of Lemon is relatively easy in experiment, such as the interference field of vector waves. As described above, MonStar is a special Lemon for which amplitude and phase are also restricted by Eq. (11), when following Eqs. (6) and (10) respectively. Eq. (11) is a function of both amplitude and phase, which means sophisticated control over phase (or amplitude) is needed to generate Mon-Star. However, in previous studies aiming to generate PSs [8-13], there has been almost no purposeful control over amplitude and phase around C-points. More constraints on amplitude and phase also illustrate that there exists a smaller probability to generate Mon-Star than Lemon in experiments. As Mon-Star, the constraints for generating Star imply that it is also very rare. However, in many studies, fields with Stars are very common.

To explain this phenomenon, we consider a point Q moving on σ anticlockwise from the −y axis. Taking the Lemon in Fig. 2(d) for example, the angle Θ_Q1 between and the +x axis and the azimuthal angle Θ_Q2 of the ellipse at Q are analyzed. Fig. 3 is a graph of Θ_Q1 and Θ_Q2 with respect to the azimuth θ_Q of Q. The dashed red and solid blue lines are Θ_Q1(θ_Q) and Θ_Q2(θ_Q) respectively. The points Q making Θ_Q1(θ_Q) and Θ_Q2(θ_Q) intersect are places where the major axes of the ellipses point to O. Because the radius of σ is very small, the transmission line between O and Q is a ray emanating from the C-point. That is, the number of intersections of Θ_Q1(θ_Q) and Θ_Q2(θ_Q) determines the number of lines of the PS. Fig. 3(a) is the relationship for the Lemon, where Θ_Q1 and Θ_Q2 intersect at only one point, θ_Q=−π/2 (3π/2), which means there is only one line emanating from the C-point for the Lemon. Fig. 3(b) is the relationship for the Mon-Star. The two lines in Fig. 3(b) have the same tendency as in Fig. 3(a), except that there are two other intersections, so there are three lines emanating from the C-points for the Mon-Star. The contribution of Eq. (11) is to modulate the slope of Θ_Q2(θ_Q) and make it intersect with Θ_Q1(θ_Q) at two additional points. This also illustrates the necessity of Eq. (11) for generating Mon-Star. Fig. 3(c) is the relationship for the Star. The solid blue line illustrates that Θ_Q2 is a decreasing function, so Θ_Q2 and Θ_Q1 still intersect in three points, even if Eq. (11) is absent. Eq. (11) is not a necessary condition for generation of the Star; this is why the presence of Stars in experiments is very common. However, for specific Stars, such as when θ_OL1 and θ_OL2 need to be specific values, the condition of Eq. (11) is indispensable.

Now we have seen that Eqs. (6) and (10) are necessary conditions for generating Lemon. Lemon can transform into Mon-Star while the amplitude and phase also follow Eq. (11). For generating Star, Eqs. (6) and (10) are also necessary conditions, while Eq. (11) is not. According to Eqs. (6) and (10) and Figs. 2(d) and (f), the amplitudes of Lemon and Star have the same distribution, while the phase differences have opposite distribution trends. Thus Lemon (Star) can transform into Star (Lemon) if the phase difference of light is modulated by transmission media, such as anisotropic media or a spatial light modulator (SLM).

The purpose of this section is to simulate some specific PSs, such as and with given values. The construction of amplitudes and phases according to sections II and III is a crucial step in generating the desired PSs. We consider the polarization ellipses in a cross section of dimensions 2b×2b. For convenience but without loss of generality, we assume that the component E_x is a plane wave, i.e. A_x = 1 and α_x = 0; then Δ is equal to α_y. Following the distribution formulas for amplitude and phase, functions that are monotonic in the studied cross section can be very simple and useful.

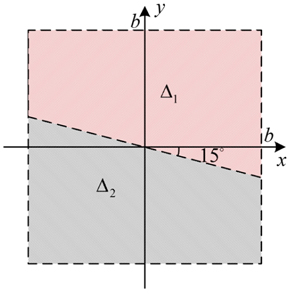
For generating the Lemon, the simplest case is when , , , and coincide with −y, +x, +y, and −x, respectively. One set of expressions for this case is A_y = −y/c+1, Δ=π(x/d+1)/2 (c≥b, d≥b). Here, we present an asymmetric Lemon whose has an angle of 60° with the +x axis, shown in Fig. 4. The background represents the light intensity, and the green ellipses show the distribution of polarization states. is the only line of the Lemon. The azimuthal angles of ellipses on is 0°. The rays and , where the azimuthal angles of ellipses are 135° and 45°, are also marked with dashed yellow lines. The amplitude used to generate Fig. 4 is A_y = −y/c+1 (c≥b), while the phase difference is shown in Fig. 5. The phase difference is divided into two regions by a line y = tan(−15°)･x: the pink region, denoted as Δ₁, and the black region, denoted as Δ₂, expressed by

where . Although Δ₁ and Δ₂ have different expressions, we emphasize that they are equal to each other at the boundary y = tan(−15°)･x, which means the phase difference shown in Fig. 5 is continuous. Eq. (13) is not the only formula that follows Eq. (10).

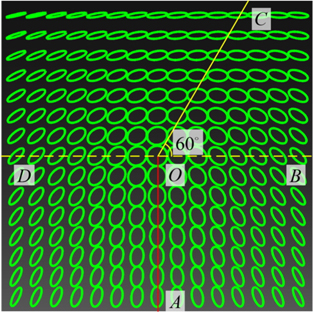
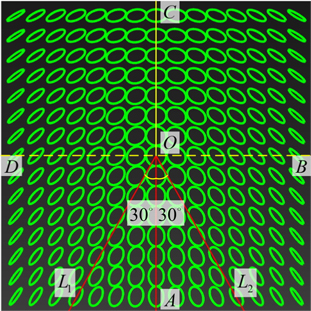
To generate Mon-Star, we can set the amplitude as A_y = −y/c+1 (c≥b) in the case of and . Then we simulate the PS shown in Fig. 6 by substituting and into Eq. (12). In Fig. 6, and coincide with −y and +y, and and make angles with +x as expected. This certifies the correctness and usefulness of Eq. (12) for generating PSs with and of given values.

We know that the two conditions of Eqs. (6) and (10) determine the generation of a Star, while another formula, Eq. (11), is needed to generate a specific Star. Figure 7 is a Star with A_y = −y/c+1 and Δ=π(−x/c+1)/2 (c≥b, d≥b). These distributions of amplitude and phase do not follow Eq. (11); however, we find that Fig. 7 is still a Star. Here, we note that the curves and are no longer linear. This phenomenon raises a doubt: Must the curves emanating from the C-point be linear? We do not discuss this question here.

There is a special case, namely that of and , in which Eq. (11) can be rewritten as A_x=A_y at and , which means and coincide with and respectively. Then the three constraints for generating a Star resolve into two constraints. In this case, Eq. (12) is no longer suitable. One expression for the amplitude and phase is

where c > 1 and d ≥ b. Figure 8 is the simulation of a Star with and coinciding with and respectively. Actually, there is an analogous case in generating Mon-Star, in which and coinciding with and respectively

By establishing a Cartesian coordinate system with origin at a C-point, and with the help of four curves where the azimuthal angles of polarization ellipses are 0°, 45°, 90°, and 135°, the distributions of amplitude and phase around C-points are analyzed and given. We also discuss the necessity of these constraints, which illustrates that there exists a smaller probability to generate Mon-Star than to generate Lemon or Star in experiments. The transformations of these three PSs are also discussed. Suitable modulation of phase difference can make Lemon (Star) transform into Star (Lemon). Compared to [7], PSs with desired shapes can be generated using the constraints obtained in this paper. According to constraints on amplitude and phase, we construct suitable functions and simulate several particularly shaped PSs. These simulations certify the correctness of the analysis and discussions. With the development of modulation techniques for amplitude and phase, it is clear that the distributions of amplitude and phase around C-points are helpful to generate arbitrarily shaped C-points in experiments.