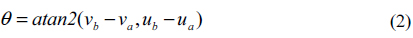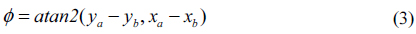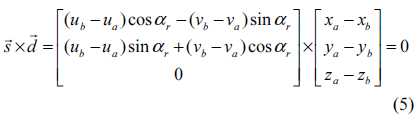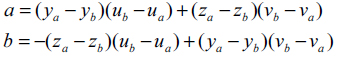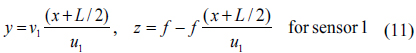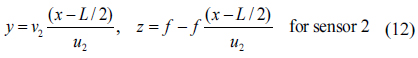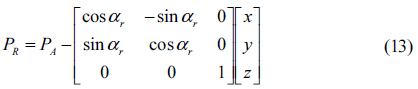Visible light communication (VLC) is regarded as one of the most promising alternatives to radio wave communication [1, 2]. Since VLC can be a solution of the broadband home network, the IEEE 802.15 Working Group for Wireless Personal Area Networks developed a standard for VLC [3]. For efficient illumination and high-speed transmission, several modulation schemes and LED lamp arrangements were studied [4-7]. In recent years, the utilization of VLC for indoor localization has received attention from many researchers. The advantages of utilizing VLC for an indoor positioning system are that the existing infrastructure can be utilized, and the achievable accuracy is not dependent upon transmission bandwidth.

Sertthin et al. [8] developed an indoor positioning system based on visible light communication identification (VLID) and a 6-axis sensor. The switching estimated receiver position (SwERP) scheme yields high accuracy even with wide field-of- view (FOV). The SwERP improves the position accuracy by optimizing the estimated distance error, which varies in proportion to the receiver’s tilt angle. An indoor positioning and communication platform using fluorescent light communication and a nine-channel receiver has been proposed [9]. Location estimation in this system requires at least three fluorescent lamps, to be detected by the photo sensor, which implies some limitations in indoor positioning. Also, indoor positioning schemes based on VLC and image sensors have been researched [10-13]. High-accuracy indoor positioning using visible LED lights and an image sensor has been proposed [10]. Each LED in a lighting fixture sends a differential three-dimensional space coordinate, and an image sensor receives the signals. This scheme uses a collinearity condition to relate the three-dimensional space coordinate data of the LEDs to the two-dimensional coordinate data of the image sensor. Indoor positioning of vehicles using an active optical infrastructure has been proposed [11]. The proposed positioning system consists of a network of beacons which transmit position signals via infrared channels to multiple mobile receivers. The mobile receiver detects the contents, transmission direction and angle of arrival of the position signal utilizing a receiver that consists of a photo detector and an image sensor device. Indoor positioning using lighting LEDs and two image sensors has been proposed [12]. In this scheme, four LEDs transmit their three-dimensional coordinate information, and a mobile receiver with two image sensors demodulates the information and calculates the indoor position from the geometrical relations of the LED images created on the image sensors. A highly precise indoor positioning algorithm using lighting LEDs, an image sensor, and VLC has been proposed [13]. In this scheme, three LEDs transmit their three-dimensional coordinate information, which is received and demodulated by a single image sensor at an unknown position.

In this paper, we present a novel indoor positioning system using lighting LEDs and a dual image sensor. Lighting LEDs transmit their three-dimensional position information using VLC technology, and a mobile receiver with a dual image sensor performs indoor positioning. The proposed indoor positioning algorithm requires position information from two LEDs and provides the three-dimensional position and azimuth angle of the mobile receiver. The rest of this paper is organized as follows. Section II provides an indoor position estimation algorithm using two LEDs and two image sensors. The proposed algorithm provides the three-dimensional position and the yaw angle of the mobile receiver. Section III shows simulation results for the proposed indoor positioning algorithm and for the conventional method with vector estimation. Especially, the mean absolute positioning error and azimuth angle error are considered. Section IV shows experimental results for the developed indoor positioning system. Final conclusions are covered in Section V.

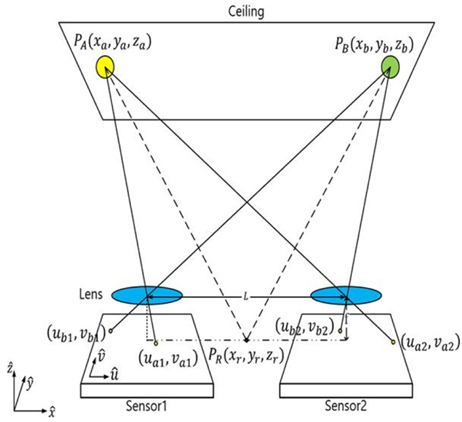
We consider an indoor position estimation model which is shown in Fig. 1. Each LED broadcasts its position information using VLC technology, and a mobile receiver with a dual image sensor is located at the bottom level. The variables are described as follows: P_A and P_B are three-d imensional position vectors of the LEDs, P_R is the center of the mobile receiver which is the midpoint between the two image sensors, is the horizontal axis on the image sensor, is the vertical axis on the image sensor, (u_a1, v_a1) and (u_a2, v_a2) are respectively the projected local positions of LED P_A on the image sensor 1 and the image sensor 2, (u_b1, v_b1) and (u_b2, v_b2) are respectively the projected local positions of LED P_B on the image sensor 1 and the image sensor 2, L is the distance between the centers of the two lenses, and f is the focal length of the lenses.

For indoor position estimation, identification of the projected position vectors of the LEDs on the dual image sensor are performed using VLC technology. The proposed indoor position estimation scheme is as follows. First, rotation angle α_r about the z-axis of the mobile receiver is calculated using the projected position vectors of two selected LEDs. Second, the directional distance vector P_R - P_A between the position vector P_A of an LED and the position vector P_R of the mobile receiver is estimated. Finally, the indoor position estimation of the mobile receiver is performed using the three-dimensional position vector P_A and the estimated directional distance vector P_R - P_A.

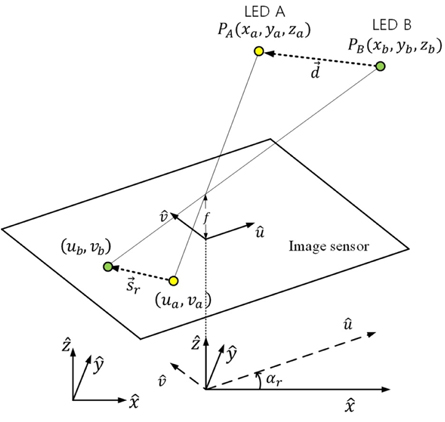
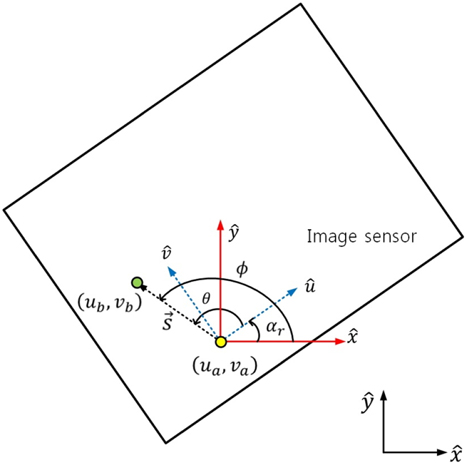
We assume that identification of the projected LED points on the dual image sensor are already performed. Projected two-dimensional position vectors of two LEDs on an image sensor are shown in Fig. 2. If more than two projected LED points are shown in an image sensor, any two points can be selected for the rotation angle estimation. Let LED A and LED B be selected for rotation angle estimation. Then, the projected points of LED A and LED B are (u_a, v_a) and (u_b, v_b) respectively. Vector and the rotation angle θ of the vector in the receiver coordinate system are calculated as follows:

where atan2(y, x) computes tan^-1(y / x) but uses the signs of both x and y to determine the quadrant in which the resulting angle lies. Because the mobile receiver knows the global position vectors of LED A and LED B using VLC technology, the rotation angle ϕ of the vector in the global coordinate system is calculated as follows:

Figure 3 shows LED mapping and the global azimuth angle on an image sensor. The rotation angle of the receiver coordinate system from the world coordinate system is obtained as

The rotation matrix R(α_r) transforms the vector from the receiver coordinate into world coordinate, and the cross product of the two parallel vectors and can be expressed as

From (5), the trigonometric equation is expressed as

with

Because the z-axis of the receiver coordinate system is parallel to the z-axis of the global coordinate system, we can estimate the rotation angle of the mobile receiver as

We assume that LED A is used for position estimation of the mobile receiver. Let (x, y, z) be the unknown position vector of LED A in the receiver coordinate system, (u₁, v₁) is the projected position of the LED on the sensor plane of sensor 1, and (u₂, v₂) is the projected position of the LED on the sensor plane of sensor 2. Then, the collinearity equations are given as follows:

where (-L/2, 0, f) is the center of the lens of sensor 1 and (L/2, 0, f) is the center of the lens of sensor 2. The above two collinearity equations intersect at (x, y, z) which is the position of the LED. Hence, the x-axis distance of LED A in the receiver coordinate system is given as follows:

Equations (8) and (9) give y-axis and z-axis distances for LED A in the receiver coordinate system as follows:

By choosing one of Equations (11) and (12) for a non-zero denominator, the y-axis and z-axis values are selected. Next, by premultiplying the position vector (x, y, z)^T by the rotation matrix R(α_r), we can get the position vector P_R of the mobile receiver in the world coordinate system as

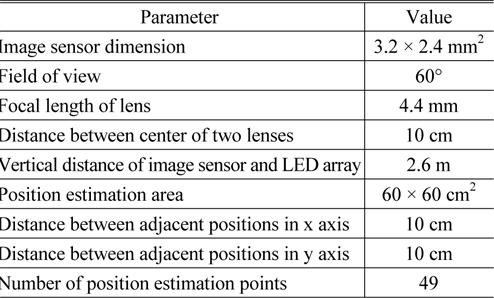
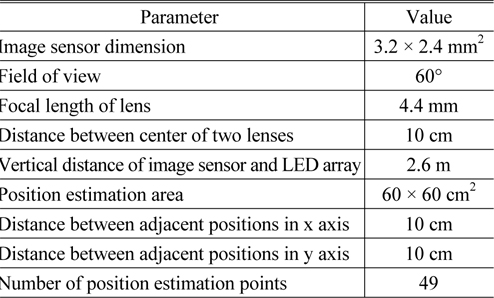
The simulation of the proposed indoor positioning algorithm was performed using MATLAB. In our simulation, a 1×1m² LED array is considered for the LED lighting and VLC transmitter. Simulation parameters such as the image sensor dimension, the field of view (FOV) of the image sensor, the distance between the centers of the two lenses, and the positioning area of the mobile receiver are listed in Table 1. The positioning error is calculated by applying Euclidean norm of the error vector as follows:

where is the estimated position vector of the mobile receiver.

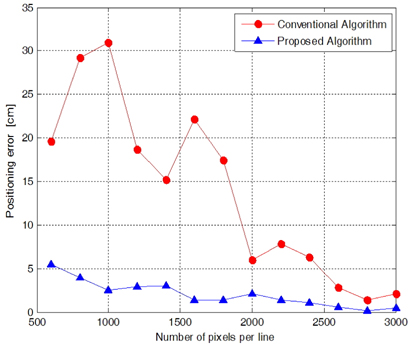
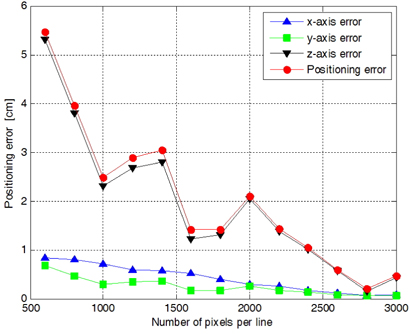
Figure 4 shows the mean absolute positioning error of the proposed positioning algorithm and the conventional positioning algorithm with vector estimation [12]. The number of pixels per line of the image sensor is increased from 600 to 3000 with a step of 200 pixels. For the conventional positioning algorithm with vector estimation, the mean absolute positioning errors for 1000, 1600, 2200, and 3000 pixels per line are 31.02 cm, 21.83 cm, 7.84 cm, and 2.13 cm, respectively. The positioning error shows decreasing zigzags as the number of pixels per line is increased. This is due to the quantization error at the image sensors [12]. With the proposed algorithm, the mean absolute positioning errors for 1000, 1600, 2200, and 3000 pixels per line are 2.49 cm, 1.41 cm, 1.43 cm, and 0.46 cm, respectively. Because of the quantization error, the proposed positioning algorithm also shows zigzagging of the positioning error with the number of pixels per line. However the positioning error of the proposed algorithm is greatly decreased in comparison with the conventional algorithm with vector estimation. That means that proposed algorithm is superior to the conventional method in indoor position estimation.

Figure 5 shows the mean absolute positioning errors of the x axis, y axis, and z axis when the proposed positioning algorithm is applied. In this case, azimuth angle of the mobile receiver is assumed to be zero. Due to quantization error, all of the positioning errors show zigzags with regard to the dependency on the number of pixels per line. When the number of pixels per line is 3000, the mean absolute positioning error is 0.09 cm, 0.08 cm, and 0.44 cm along the x axis, y axis, and z axis, respectively. Hence, we know that the errors along the x axis and y axis are much lower than that of the z axis.

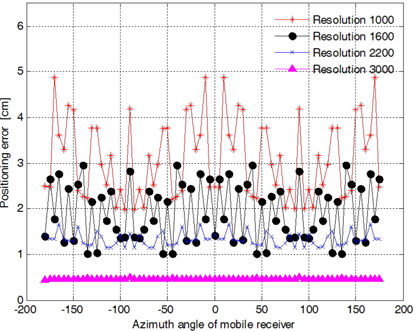
Figure 6 shows the mean absolute positioning error of the proposed positioning algorithm along the azimuth angle, which is increased from -180 degrees to 175 degrees with steps of 5 degrees. The positioning error along the azimuth angle shows a random distribution. That means that the positioning error has no dependency on azimuth angle. We also know that the mean absolute positioning error and the variation of the range of error are reduced when the number of pixels per line is increased.

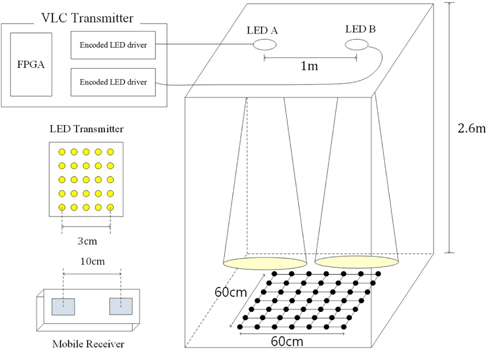
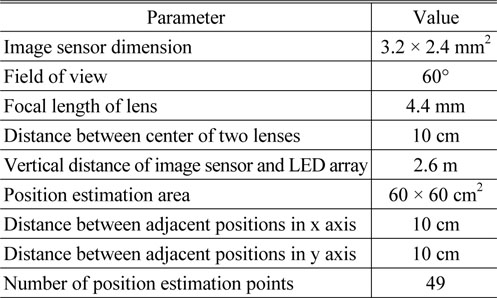
We developed an indoor positioning system and demonstrated the proposed indoor positioning algorithm. Figure 7 shows the experimental model room for the indoor position experiment. The height of the model room is 2.6 m. Two LED lamps are located at the ceiling and are separated by 1 m. Each LED lamp is assembled with 5 × 5 white LEDs and the diameter of each LED is 5 mm. Each LED lamp is modulated for lighting and VLC communication, and the VLC transmitter of each LED lamp performs on-off keying (OOK) modulation to broadcast its position information. A mobile receiver is located at the bottom of the model room, and 7 × 7 points are selected for the indoor position experiment. A mobile receiver is developed for VLC communication and is composed of two Logitech 310 webcams. The dimension of each image sensor is 3.2 × 2.4 mm², and the distance between centers of the two lenses is 10 cm. In this experiment, two LED lamps broadcast that position information using VLC technology. Hence, identification of the projected LED lamps on the dual image sensor is performed. Some experimental parameters are listed in Table 2.

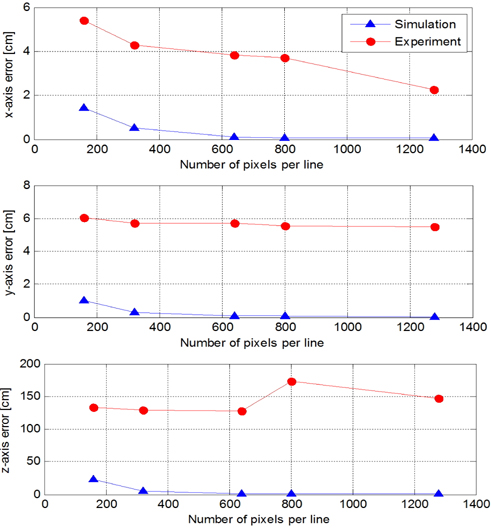
Figure 8 shows the mean absolute positioning error of the developed indoor positioning system at five resolutions: 160 × 120, 320 × 240, 640 × 480, 800 × 600, and 1280 × 960. The simulation errors along the x axis, y axis, and z axis at 160 × 120 resolution are 1.45 cm, 1.03 cm, and 22.3 cm, respectively. The experimental errors along the x axis, y axis, and z axis at 160 × 120 resolution are 5.4 cm, 6.05 cm, and 1.33 m, respectively. When the resolution is 1280 × 960, the simulation errors along the x axis, y axis, and z axis are 0.07 cm, 0.02 cm, and 0.32 cm, respectively. The experimental errors along the x axis, y axis, and z axis at 1280 × 960 resolution are 2.26 cm, 5.51 cm, and 1.46 m, respectively. The experimental errors are much higher than those of the simulation results. This is because the broadcast of position information is performed not by each LED but by each LED lamp. The errors in finding the centers of LED lamp images, measurement errors, and quantization errors increase the indoor positioning experimental errors. Especially, the z-axis error is dominant over the x-axis and y-axis errors. This is because the indoor position estimation on the z-axis is dependent on the estimated x-axis and y-axis values.

In this paper, we proposed an indoor position estimation algorithm using LEDs and a dual image sensor. Each lighting LED broadcasts its position information using VLC technology and a mobile receiver with a dual image sensor estimates its three-dimensional position and azimuth angle from the broadcast positions of the two LEDs. Using MATLAB simulation, we showed that the proposed indoor position estimation method gives more accurate positioning results than the conventional method with vector estimation.

Next, we developed an indoor positioning system and demonstrated its performance. From the results of the experiment, the mean absolute positioning error of the z-axis is dominant over x-axis and y-axis errors. The planned future work is to improve the z-axis positioning error of the proposed indoor positioning system.