2차원 쐐기형 제어핀 후류의 공동유동 특성에 대한 실험연구

doi:10.3744/SNAK.2016.53.3.180

OA학술지
Journal of the Society of Naval Architects of Korea

2차원 쐐기형 제어핀 후류의 공동유동 특성에 대한 실험연구 An Experimental Study on Wake Cavity Flow Characteristics of Two-dimensional Wedge Shaped Control Fins

DOI : 10.3744/SNAK.2016.53.3.180
Publish: Journal of the Society of Naval Architects of Korea Volume 53, Issue3, p180~187, 20 June 2016

ABSTRACT

As distinct from a slender body, the separation of the boundary layer on a bluff body give rise to complex wakes in which various kinds of vortices form, develop and interact with each other. In this paper, we investigate cavitation wake field behind wedge shaped two-dimensional fin models. Eight different models are tested at the Chungnam National University Cavitation Tunnel (CNU-CT). First, we measure wake cavity shapes and compare with numerical results, which shows the good agreement with each other. In addition, we demonstrate that wake flow characteristics of the control fin are clearly identified by the correlation analysis of high-speed camera images and pressure fluctuation measurements.

KEYWORD

2차원 쐐기 , 제어핀 , 후류 유동 , 캐비테이션 공동

본문

Collapse all

1. 서 론

수중에서 이동하는 운동체에서 발생하는 공동(cavitation) 현상은 익히 잘 알려져 있는 물리적 현상이다. 공동이 발생하면 운동체의 추진 효율이 감소되고 소음이 증가하며 표면이 침식되는 등의 폐해가 발생할 수 있기 때문에 그동안 이를 제어하기 위한 연구가 이루어져 왔다. 하지만 최근 들어 자연적 또는 인공적으로 공동을 생성시켜 수중 운동체 전체를 감싸게 하여 항력을 감소시킴으로써 고속 주행을 가능케 하는 초공동(supercavitation) 수중운동체 기술에 대한 관심이 높아지고 있으며 그에 대한 이론 및 실험 연구들(Ahn, et al.,2010; Ahn, et al.,2012)이 이루어지고 있다. 초공동 수중운동체는 최소 200노트 이상의 고속으로 이동하기 때문에 초공동을 생성시키고 유지시키는 기술과 함께, 고속 수중운동체를 제어하는 기술이 핵심 요소라 할 수 있다. 일반적으로 초공동 수중운동체의 심도 및 방향 제어를 위해 운동체의 전두부(forehead)에 위치한 캐비테이터(cavitator)와 뒤쪽에 상하 좌우로 위치한 네 개의 쐐기 형상을 갖는 제어핀이 사용된다. 이때 운동체의 좌우 제어핀은 심도를 제어하며, 상하 제어핀은 방향을 제어하는데 사용된다. 초공동이 발생한 상태에서 이들 제어핀의 일부분은 공동 속에 있으며, 나머지 일부는 물과 접촉된 상태에서 작동하게 된다. 따라서 접수 정도와 받음각의 변화에 따른 제어핀 주위의 유동과 작용하는 하중 특성에 대한 연구가 필요하다.

본 논문은 초공동 수중운동체의 제어핀 주위 유동에 대한 기초연구의 일환으로 수행된 2차원 쐐기형 제어핀 후류에서 발생하는 공동유동 특성에 대한 실험결과를 다루고 있다. 일반적인 2차원 쐐기 형상의 몰수체에서 발생하는 공동현상에 대한 실험 및 이론연구(Waid,1957; Plesset & Shaffer, 1948; Kim et al.,2013)는 오래 전부터 수행되어 왔지만 운동체 후류에서 발생하는 공동유동의 특성에 대한 정량적인 실험 데이터는 상대적으로 부족한 실정이다. 본 연구에서는 다양한 형상의 2차원 쐐기형 제어핀의 후류에서 발생하는 공동유동의 형성 과정을 초고속 카메라를 이용하여 면밀하게 관측하였고, 유동장에서 발생하는 변동압력을 계측하여 후류의 주기적인 와유동(periodic vortical flow) 특성을 평가하고자 하였다. 또한 초고속 영상 자료와 변동압력 계측 값의 상관관계를 분석하여 2차원 쐐기형 제어핀의 후류에서 발생하는 공동유동의 형성 과정을 정량적으로 평가하고자 하였다.

2. 쐐기형 몰수체 후류의 유동 특성

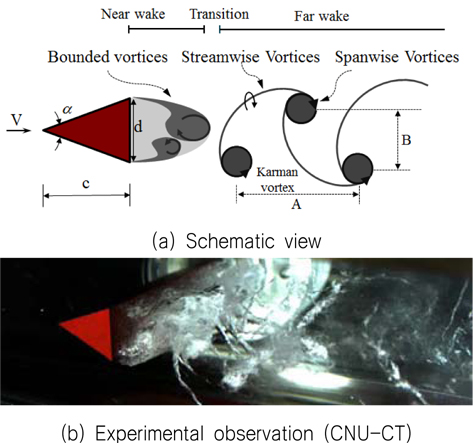
잘 알려져 있는 것처럼 몰수체(submerged body)의 후류에서는 Karman 와열(Karman vortex street)이라 불리는 주기적 특성을 갖는 와류가 형성된다. 상대적으로 무딘 물체(blunt body)의 경우 경계층이 박리되어 넓은 범위의 와류가 생성되어 발달하며, 와류가 강해지면 그 중심에서의 압력강하(pressure drop)에 따라 공동이 형성되어 와류들의 상호간섭이 보다 명확하게 나타난다. Fig. 1은 쐐기 형상의 몰수체에서 발생하는 후류 공동유동 특성을 보여준다. 박리된 공동유동은 가까운 후류(near wake) 영역에서 닫힌 와류(bounded vortices)를 형성하며, 천이영역을 거쳐 상대적으로 먼 후류(far wake) 영역에서는 유동방향 와류(streamwise vortices)와 횡방향 와류(spanwise vortices)의 주기적 조합인 Karman 와열이 형성된다.

[Fig. 1] Characteristics of wake cavitation of a wedge shape submerged body

3. 실험 장치 및 모형

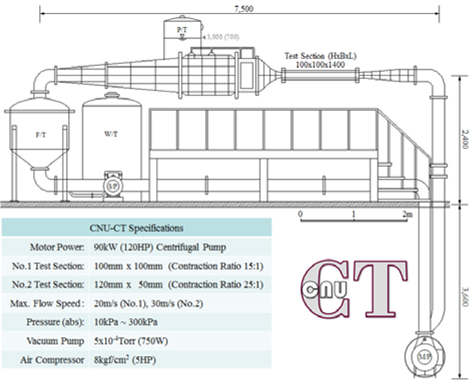
실험은 충남대학교 캐비테이션 터널(Fig. 2)에서 수행되었다. 시험부 단면은 100mm x 100mm, 길이는 1400mm 이며 최대 유속은 20m/s이다. 가압 및 감압 장치를 통해 터널 내부의 압력은 최소 10kPa에서 최대 300kPa 까지 조절 가능하다.

[Fig. 2] CNU-CT specifications

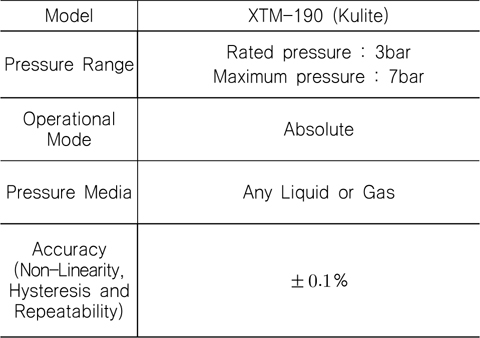
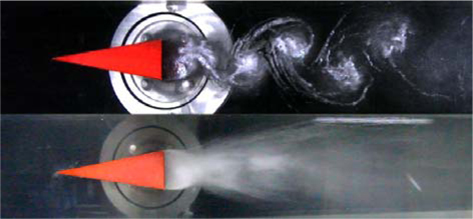
2차원 제어핀 후류의 주기적 유동 특성을 파악하기 위해 Fig. 3에서와 같이 관측창 상부에 변동압력 센서(Kulite사의 XTM-190)를 설치하여 계측하였으며, 센서의 주요 제원은 Table 1에 나타내었다. 또한 후류 유동 특성과 공동의 생성 과정을 보다 엄밀하게 관찰하기 위해 초고속 카메라(Photron사의 FASTCAM-UX100 800,000fps)를 사용하였다(Fig. 4). Fig. 5는 동일 조건에서 초고속 카메라와 일반 DSLR 카메라로 촬영한 이미지로, DSLR 의 경우 육안으로 관찰할 수 있는 수준과 비슷하지만, 초고속 카메라 이미지의 경우 공동의 발생 및 성장 과정을 보다 엄밀하게 관찰할 수 있음을 보여준다.

[Fig. 3] Pressure fluctuation sensor equipped on the top of the test section

[Table 1] Specifications of the pressure fluctuation sensor

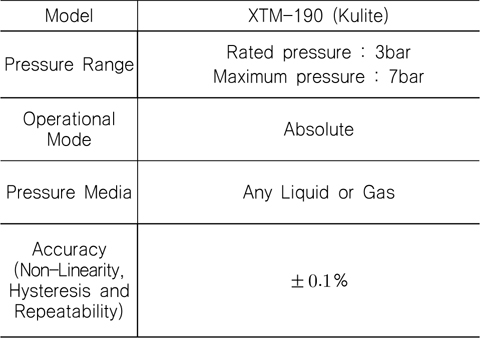
Specifications of the pressure fluctuation sensor

[Fig. 4] High speed camera and lights system

[Fig. 5] Typical cavitation images recorded by a high speed camera (Top) and a general DSLR camera (Bottom)

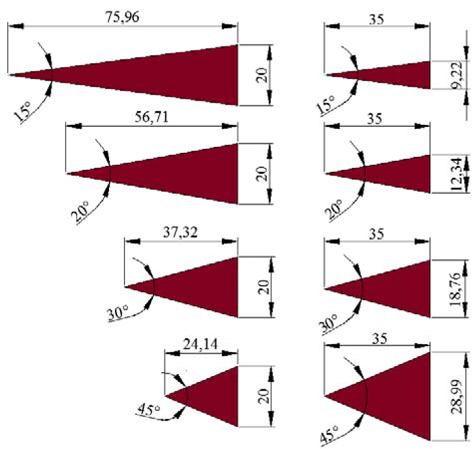
실험 모형은 제어핀 각(α)이 15° , 20° , 30° , 45° 인 경우에 대해 두께(d)와 코오드 길이(c)를 각각 20mm, 35mm로 고정한 총 8종의 2차원 쐐기형 제어핀을 사용하였으며 모형의 폭은 100mm로 터널의 양쪽 벽면에 고정시켜 2차원 유동을 구현하였다. 본 논문에서는 d = 20mm로 고정한 모형을 Group 1(G1)로, c = 35mm로 고정한 모형을 Group 2 (G2)로 구분하였다. Table 2는 각 모형의 두께와 길이를 나타내며, Fig. 6은 모형의 형상을 비교하여 보여준다.

[Table 2] Size of the test models

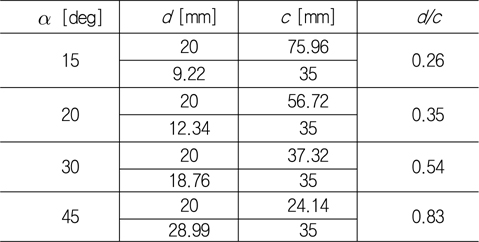
Size of the test models

[Fig. 6] Shape of the test models (unit: mm)

4. 실험 결과

4.1 제어핀 후류의 공동형상 특성

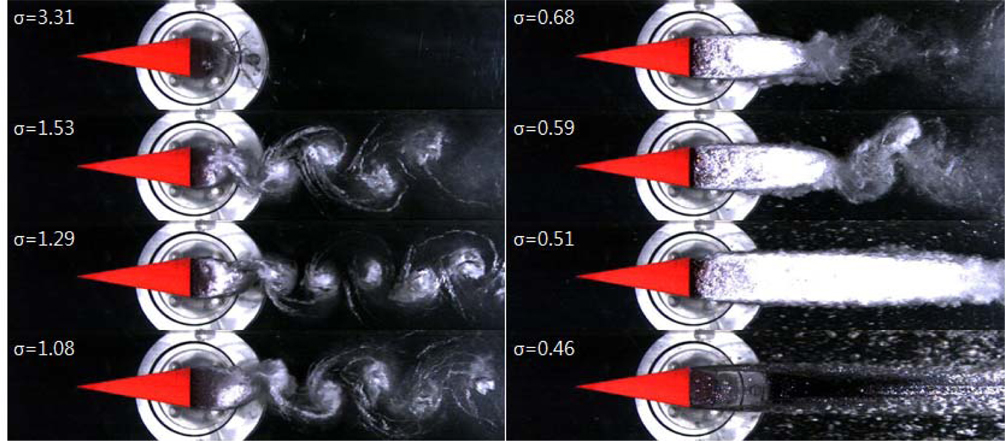
공동의 형상특성은 유동속도와 압력조건을 변화시켜가며 아래와 같이 정의된 캐비테이션수(σ)에 따라 계측하였다.

여기서, P_∞ 는 유입류의 압력, P_v는 물의 증기압, V는 유속 이다. Fig. 7은 제어핀의 가까운 후류에서 형성된 닫힌 공동와류가 캐비테이션수가 낮아지면서 성장하여 완전한 공동으로 성장하는 과정을 보여준다. 이때 Fig. 8과 같이 정의한 공동 길이(l)와 최대 두께(w)는 10,000fps로 촬영된 초고속 카메라 영상을 분석하여 측정하였다.

[Fig. 7] Development of the wake cavity

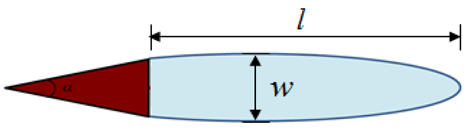
[Fig. 8] Cavity length(l) and maximum width(w)

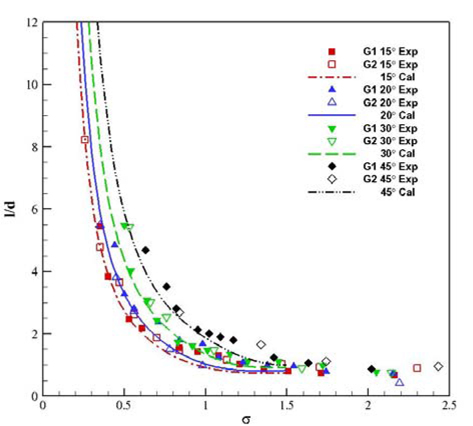
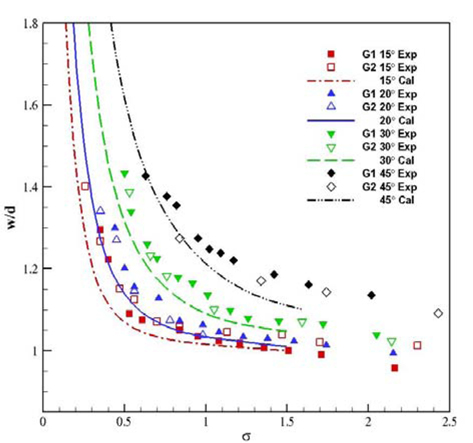
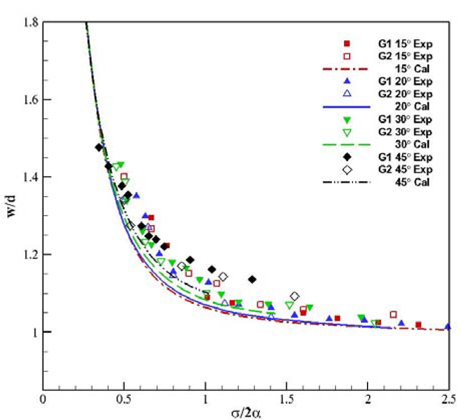
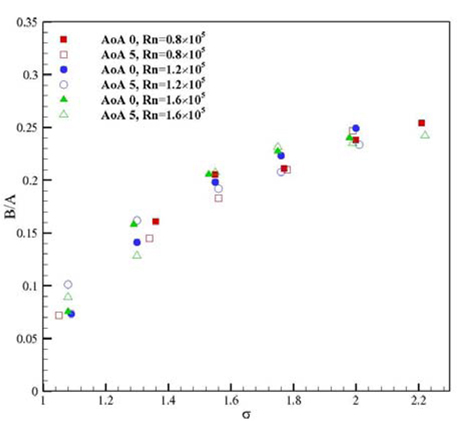
Fig. 9와 Fig. 10은 계측한 공동의 길이(l)와 최대 두께(w)를 제어핀의 두께(d)로 무차원화하여 이론해석 결과와 함께 비교하였다. 제어핀의 각도(α)에 따라 캐비테이션수가 낮아질수록 발생하는 공동의 길이와 두께가 증가하는 것을 확인할 수 있으며, 같은 캐비테이션수 조건에서 제어핀의 각도가 클수록 발생하는 공동의 길이와 두께가 커지는 것을 확인할 수 있다. 또한 제어핀의 각도가 같은 경우 형상비(d/c)에 관계없이 후류 공동의 무차원 형상은 동일하게 나타남을 확인할 수 있다.

[Fig. 9] Non-dimensional cavity length versus cavitation number according to different test models

[Fig. 10] Non-dimensional cavity width versus cavitation number according to different test models

본 연구 그룹에서는 비점성 유동해석법에 기반한 경계요소법을 바탕으로 초월공동유동을 해석할 수 있는 수치해석법을 개발하여 성능평가를 한 바 있으며(Kim et al, 2013), 본 해석법을 이용한 계산 결과와 비교적 잘 일치함을 알 수 있다.

Fig. 10에 나타낸 공동의 최대 두께는 제어핀의 각도가 커짐에 따라 일정하게 증가하는 것을 확인할 수 있는데, 이는 제어핀 각도와 함께 σ/2α의 파라미터로 정리하여 Fig. 11과 같이 나타내는 경우 다양한 제어핀의 형상비에 따라 발생하는 공동의 최대 두께를 보다 보편적으로 예측할 수 있음을 보여준다.

[Fig. 11] Non-dimensional cavity width versus σ/2α

4.2 제어핀 후류의 박리와류 특성

여러 형상의 시험 모형 중 d = 20mm, α = 20°제어핀을 사용하여 받음각과 레이놀즈수의 변화에 따른 제어핀 후류의 박리와류 특성을 초고속 카메라 영상을 분석하여 계측하였다. 레이놀즈수(Rn)는 다음과 같이 정의하며, 여기서 V는 유속, d는 제어핀의 두께이며 ν는 동점성계수이다.

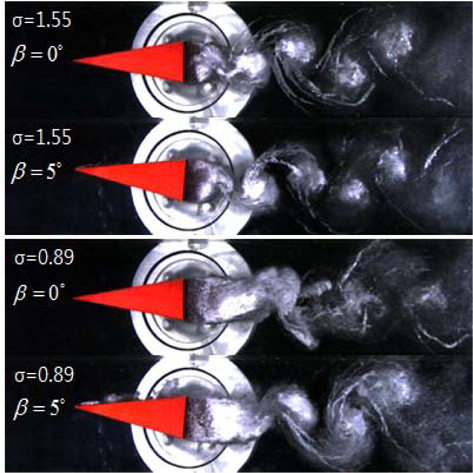
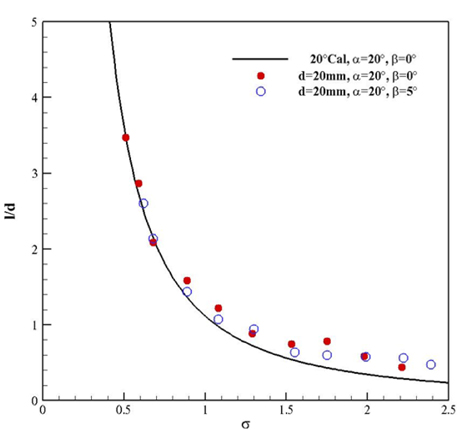
Fig. 12는 제어핀의 받음각(β)이 0도와 5도일 때 서로 동일한 캐비테이션수 조건에서 발생하는 공동을 보여주며, Fig. 13은 무차원화한 공동의 길이를 비교하여 보여준다. 이를 통해 받음각 변화에 따른 공동의 성장 과정은 큰 차이가 없으며, 공동 길이 또한 차이가 없음을 확인할 수 있다. Fig. 14는 앞선 Fig. 1에 정의된 닫힌 와류의 후류에서 박리되어 생성되는 Karman 와열의 수평방향 거리(A)와 수직방향 거리(B)의 비(B/A)를 계측하여 비교한 결과로 캐비테이션수가 감소함에 따라 닫힌 와류의 크기가 커지며 결과적으로 와열의 거리 비는 비선형적으로 감소하는 것을 확인할 수 있다. 또한 이러한 와열의 거리 비는 레이놀즈수 변화에 대해서는 큰 차이를 보이지 않음을 알 수 있다.

[Fig. 12] Comparison of cavity shapes between two different angles of attack

[Fig. 13] Non-dimensional cavity length versus cavitation number for different angles of attack

[Fig. 14] Distance ratio (B/A) versus cavitation number

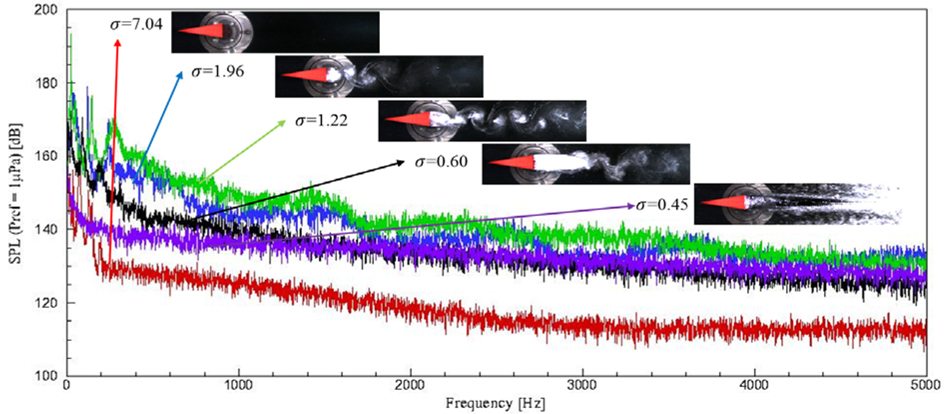
Fig. 3에서 설명한 바와 같이 관측창 상부에서 계측된 변동압력을 통해 박리와류의 주기적인 특성을 평가하였다. 계측된 변동압력 값은 고속 푸리에변환(Fast Fourier Transform, FFT)을 통해 주파수영역의 소음수준(Sound Pressure Level, SPL)으로 변환하여 비교, 분석하였다. Fig. 15는 d = 20mm, α = 20°인 제어핀의 받음각 0도에서 발생하는 공동형상과 해당 조건에서의 소음특성을 나타낸다. 여기서 σ = 7.04는 공동이 발생하지 않는 조건이며, 캐비테이션수가 낮아지면서 공동이 발달하여 σ = 1.22인 경우 닫힌 와류의 후류에서 강한 Karman 와열이 형성되며 전체 주파수 영역에서의 소음 수준이 증가하는 것을 확인할 수 있다. 캐비테이션수가 더욱 낮아져 σ = 0.60인 경우와 같이 충분히 성장한 닫힌 와류의 후류에서는 Karman 와류의 세기가 약해지며 소음수준 또한 감소하는 것을 알 수 있다. 즉, 제어핀 후류에서 발생하는 소음수준은 닫힌 와류의 후류에서 발생하는 Karman 와류의 영향이 지배적임을 알 수 있다.

[Fig. 15] Wake cavitation and induced noise characteristics

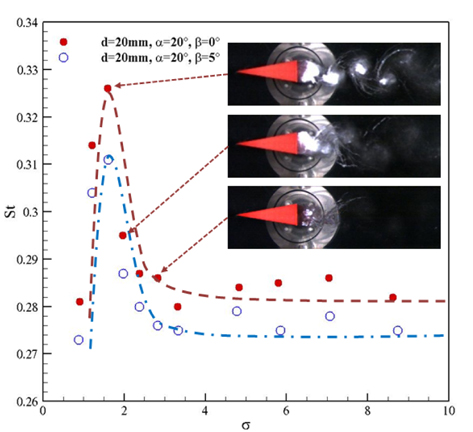
닫힌 와류와 Karman 와류의 주기적인 특성을 보다 분명히 분석하기 위해 Rn = 1.6 × 10⁵ 조건에서 캐비테이션수가 1.22인 경우에 대해 한 주기 동안 발생하는 공동 형상을 Fig. 16과 17에 나타내었다. 이 때 닫힌 와류와 Karman 와류의 발생 주기는 0.043초와 0.0077초로 주파수는 23Hz와 130Hz에 해당한다. 이러한 주파수 특성은 계측한 변동압력 특성(Fig. 18)을 통해서도 그대로 나타나고 있음을 알 수 있다. 캐비테이션수가 낮아질수록 닫힌 와류의 크기는 커지기 때문에 주파수는 낮아지는 반면 Karman 와류의 주파수는 높아지는 것을 알 수 있다. 또한 Karman 와류는 조화 주파수(harmonic frequency) 성분을 가지고 있으며 1차와 2차 조화 성분이 나타나는 것을 확인할 수 있으며, 2차 조화 성분은 Karman 와류가 소산됨에 따라 주파수 영역이 폭넓게 나타남을 알 수 있다.

[Fig. 16] Periodic motion of the bounded vortex

[Fig. 17] Periodic motion of the Karman vortex

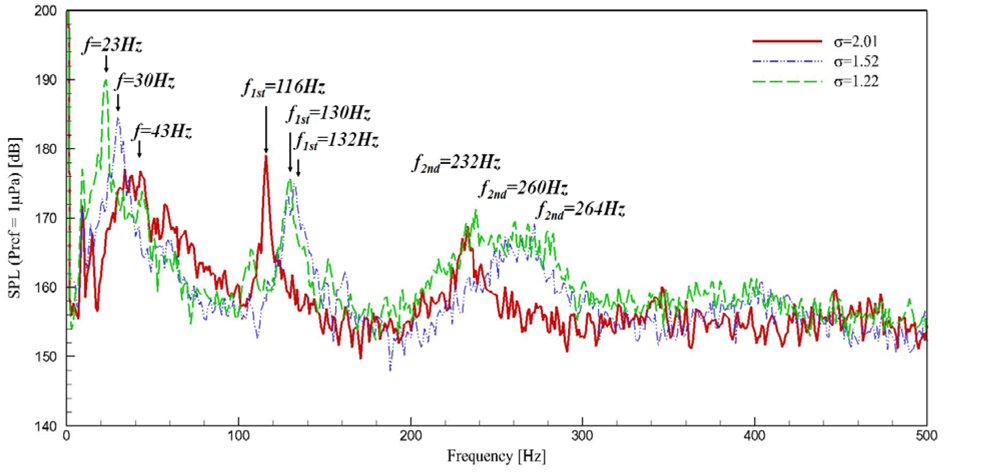
[Fig. 18] SPL versus vortex frequency

다음으로 Karman 와류의 주파수 특성을 보다 명확히 파악하기 위해 Fig. 19와 같이 유속을 증가시켜 캐비테이션수를 낮췄을 때 받음각 0도와 5도 조건에서 발생하는 Karman 와류의 주파수 특성을 살펴보았다. 여기서 실선은 V = 7.6m/s까지의 계측 값을 회귀분석한 결과로 받음각 변화에 상관없이 유속과 박리 주파수는 선형적인 관계임을 확인할 수 있다. 하지만 특정 유속 구간에서, 특히 V = 9m/s 근처에서는 박리 주파수가 최대로 증가하였다가 이후 유속에서는 다시 줄어드는 것을 확인 할 수 있다. 이러한 주파수 특성은 아래와 같이 정의되는 Strouhal(S_t)수로 무차원화 하여 Fig. 20과 같이 비교하면 보다 명확히 이해 할 수 있다.

[Fig. 19] Shedding frequency versus flow speed

[Fig. 20] Strouhal number versus cavitation number

여기서 f는 Karman 와류의 박리 주파수, d는 제어핀 두께이며 V는 유속이다. 상대적으로 높은 캐비테이션수 영역에서 Karman 와류의 주파수는 일정한 값을 갖는다. 하지만 Fig. 20의 σ = 1.22(Fig. 19의 V = 9.2m/s 에 해당)인 경우 이때 발생한 닫힌 와류의 크기는 제어핀의 두께(d)와 같은 크기로 성장하게 되고 그에 따른 후류 유동장이 형성되어 Karman 와류의 주파수가 최댓값을 나타낸다. 이후 공동이 성장함에 따라 Karman 와류의 주파수가 다시 감소하는 것을 알 수 있으며, 받음각 5도의 경우도 같은 특성이 나타나는 것을 알 수 있다. Fig. 21은 받음각 0도 조건에서 유입 유속을 각각 4m/s, 6m/s, 8m/s로 고정한 상태, 즉 레이놀즈수를 고정시키고 터널 내부 압력을 낮춰 캐비테이션수를 낮췄을 때의 주파수의 특성을 나타내며 이를 통해 확인할 수 있는 바와 같이 캐비테이션수가 높은 조건에서 Strouhal수는 일정한 값을 유지하다가 캐비테이션이 발생하는 구간에서는 약 15% 정도 증가하는 것을 알 수 있다.

[Fig. 21] Strouhal number versus cavitation number according to different Reynolds numbers

4. 결 론

본 연구는 다양한 형상의 2차원 쐐기형 제어핀 모형을 대상으로 캐비테이션터널 실험을 수행하여 후류에서 발생하는 공동유 동의 특성을 보다 정량적으로 계측하여 분석하고자 하였다. 이를 위해 초고속 카메라를 이용하여 유동을 면밀하게 관측하였고, 유동장에서 발생하는 변동압력을 계측하여 후류 유동의 주기적인 특성을 계측하였다.

본 실험연구를 통해 먼저 제어핀 후류에서 발생하는 캐비테이션의 형상을 계측하여 이론해석 결과와 비교 검증하였으며, 이를 바탕으로 제어핀의 형상비에 따라 발생하는 공동의 기하학적 특성을 정량적으로 평가하였다. 또한 제어핀 후류의 주파수 특성을 파악하고 발생하는 소음수준과의 상관관계를 해석하였다. 이를 통해 제어핀 후류에서 발생하는 소음수준은 닫힌 와류와 Karman 와류의 영향이 지배적임을 규명하였으며, 아울러 다양한 유동 조건에서 캐비테이션과 함께 발생하는 Karman 와류의 주파수 특성을 평가하였다.

참고문헌

1. Ahn B. K., Lee C. S., Kim H. T. 2010 Experimental and Numerical Studies on Super-Cavitating Flow of Axisymmetric Cavitators [International Journal of Naval Architecture and Ocean Engineering] Vol.2 P.39-44
2. Ahn B. K., Lee T. K., Kim H. T., Lee C. S. 2012 Experimental Investigation of Supercavitating Flows [International Journal of Naval Architecture and Ocean Engineering] Vol.4 P.123-131
3. Kim J. H., Jang H. K., Ahn B. K., Lee C. S. 2013 A Numerical Analysis of the Supercavitating flow around Three-Dimensional Axisymmetric Cavitators [Journal of the Society of Naval Architects of Korea] Vol.50 P.160-166
4. Plesset M. S., Shaffer P. A. 1948 Cavity Drag in Two and Three Dimensions [Journal of Applied Physics] Vol.19 P.934-939
5. Waid R.L. 1957 Water Tunnel Investigation of Two-dimensional Cavities

이미지 / 테이블

[ Fig. 1 ] Characteristics of wake cavitation of a wedge shape submerged body
[ Fig. 2 ] CNU-CT specifications
[ Fig. 3 ] Pressure fluctuation sensor equipped on the top of the test section
[ Table 1 ] Specifications of the pressure fluctuation sensor
[ Fig. 4 ] High speed camera and lights system
[ Fig. 5 ] Typical cavitation images recorded by a high speed camera (Top) and a general DSLR camera (Bottom)
[ Table 2 ] Size of the test models
[ Fig. 6 ] Shape of the test models (unit: mm)
[ ]
[ Fig. 7 ] Development of the wake cavity
[ Fig. 8 ] Cavity length(l) and maximum width(w)
[ Fig. 9 ] Non-dimensional cavity length versus cavitation number according to different test models
[ Fig. 10 ] Non-dimensional cavity width versus cavitation number according to different test models
[ Fig. 11 ] Non-dimensional cavity width versus σ/2α
[ ]
[ Fig. 12 ] Comparison of cavity shapes between two different angles of attack
[ Fig. 13 ] Non-dimensional cavity length versus cavitation number for different angles of attack
[ Fig. 14 ] Distance ratio (B/A) versus cavitation number
[ Fig. 15 ] Wake cavitation and induced noise characteristics
[ Fig. 16 ] Periodic motion of the bounded vortex
[ Fig. 17 ] Periodic motion of the Karman vortex
[ Fig. 18 ] SPL versus vortex frequency
[ Fig. 19 ] Shedding frequency versus flow speed
[ Fig. 20 ] Strouhal number versus cavitation number
[ ]
[ Fig. 21 ] Strouhal number versus cavitation number according to different Reynolds numbers