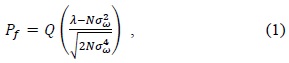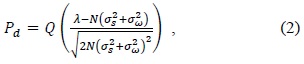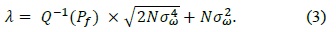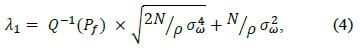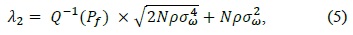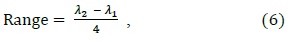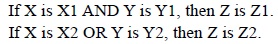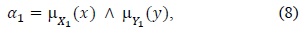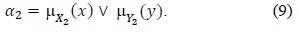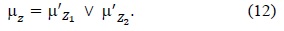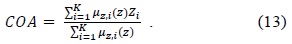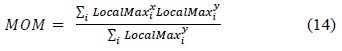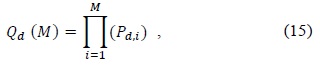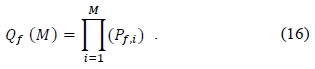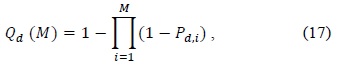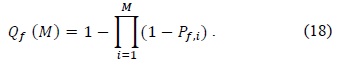Spectrum sensing in cognitive radio networks allows secondary users to sense the unused spectrum without causing interference to primary users. Cognitive radio requires more accurate sensing results from unused portions of the spectrum. Accurate spectrum sensing techniques can reduce the probability of false alarms and misdetection. In this paper, a two-stage spectrum sensing scheme is proposed for cooperative spectrum sensing in cognitive radio networks. In the first stage, spectrum sensing is executed for each secondary user using energy detection based on double adaptive thresholds to determine the spectrum condition. If the energy value lies between two thresholds, a fuzzy logic scheme is applied to determine the channel conditions more accurately. In the second stage, a fusion center combines the results of each secondary user and uses a fuzzy logic scheme for combining all decisions. The simulation results show that the proposed scheme provides increased sensing accuracy by about 20% in some cases.
Wireless networks are characterized by a fixed spectrum allocation policy. However, demand for the frequency spectrum is increasing, leading to spectrum scarcity. To overcome this scarcity in wireless communication, a cognitive radio network has been proposed. In this network, cognitive radio users, called secondary users (SU), are allowed to utilize the primary user (PU) bands when they are unoccupied but must avoid harmful interference with the primary users. To achieve this, spectrum sensing is an essential mechanism in cognitive radio networks [1]. Various techniques for spectrum sensing have been proposed in the literature, including the matched-filter technique, cyclostationary detection, and energy detection.
Energy detection is the most popular technique due to its simplicity. It does not require any prior information about the primary signal, and its sensing speed is fast. However, the performance of energy detection is limited by noise uncertainty. Furthermore, multipath fading, shadowing, and the hidden node problem degrade the performance of single-user spectrum-sensing techniques [2]. To overcome these problems, cooperative sensing was introduced as a solution. In this technique, secondary users collaborate to sense the unused spectrum and detect a PU signal. Then, with or without sharing information about the local decision, they forward the local decision results to the fusion center. The center then decides the final result according to the decision rules applied in the fusion center [3]. Various techniques have been proposed to mitigate noise uncertainty such as double threshold-based sensing. However, if all the energy lies between two thresholds, spectrum sensing will fail [4]. Due to the uncertainty in noise power, accurate detection becomes impossible, and choosing a suitable threshold in spectrum sensing becomes more difficult.
In this paper, a new two-stage spectrum sensing scheme using fuzzy logic for cognitive radio networks is proposed. In the first stage, spectrum sensing is executed at the local node based on a double adaptive threshold scheme. If the measured energy lies between the two thresholds, the actual channel condition is decided based on a fuzzy logic scheme to mitigate the sensing failure problem. After local spectrum sensing is performed, each secondary user sends their local decision results to the fusion center. In the second stage, this fusion center combines all the local decision results using fuzzy logic and gives the final decision.
The first energy detection technique was proposed by Urkowitz in 1967 [5]. He proved that energy detection is a simple technique and does not require complex computation. Despite its simplicity, the performance of energy detection is limited by noise uncertainty. In addition, the multipath, shadowing, and hidden node problems degrade the performance of single-user spectrum-sensing techniques. One possible technique to overcome these problems is cooperative sensing [3]. The main idea of this technique is that secondary users interact with each other to determine the availability of a channel after individual measurement of the channel. In contrast, the adaptive spectrum sensing technique, which is based on the dynamic selection threshold using the constant false alarm rate (CFAR) scheme, was proposed to enhance the spectrum sensing capability in a low signal to noise ratio (SNR) [6].
The two threshold sensing technique was introduced to mitigate noise uncertainty. However, the problem of a “confused region” remains in which all the detected energy values lie between two thresholds. Thus, the secondary users cannot decide whether the primary users are present or not. In this case, the spectrum sensing procedure will fail. In [7], the author proposed an “n-ratio” based logic with two thresholds. If all the detected values are between the two thresholds, the secondary user sends a “no decision” to the fusion center, and the fusion center helps the secondary users to determine the actual state of the spectrum. In [8], the author proposed hierarchical cooperative spectrum sensing based on double threshold energy detection. In this scheme, if the collected energy value lies between the two thresholds, it requires the fusion center to make a final decision. The fusion center quantizes the local value into four two-bit decisions and combines them to give the final decision. In contrast, because the performance degrades sharply as the noise uncertainty increases, a dynamic threshold algorithm was proposed to combat noise uncertainty [9]. In [10], the author solved the sensing failure problem at a local node using two-bit quantization. The scheme is used to divide the confused region into four equal quantization intervals with the same weight. A three threshold scheme was proposed to mitigate the confused region based on the dynamic threshold factor [11].
Another approach to research has been to apply fuzzy logic to cognitive radio networks. This technique can provide a framework to handle ambiguity and vagueness. A fuzzy decision chooses the most appropriate access opportunity by using cross-layer information, past history, and shared knowledge among different devices through a knowledge base. Cognitive spectrum sensing based on fuzzy logic was presented in [12]. This approach provides good sensing performance and high flexibility for decision combining at the fusion center. In [13], the author proposed a spectrum sensing scheme with fuzzy logic that is applied in the local node. In this scheme, the author performs three different spectrum sensing techniques simultaneously in the local node. Then, the probability of detection (
III. PROPOSED SPECTRUM SENSING SCHEME
The spectrum sensing scheme used in this paper is based on the double adaptive threshold scheme. The consideration for using energy detection with double adaptive thresholds is that this scheme can mitigate uncertainty in noise power. In the conventional single threshold case, the false alarm probability (
where
According to the single threshold, we can derive two different thresholds, the lower threshold (
where
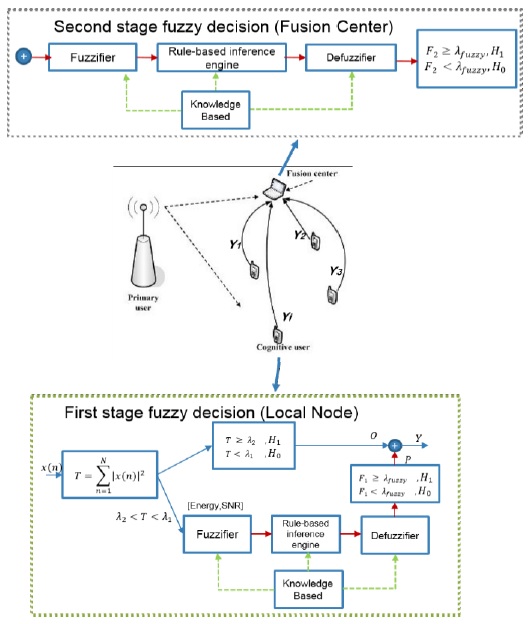
The overall procedure of the proposed scheme is shown in Fig. 1. Each process in Fig. 1 is described below.
>
A. First Stage (Local Decision)
(a) Each secondary user senses the primary user’s signal and decides based on a double adaptive threshold. If the energy is larger than
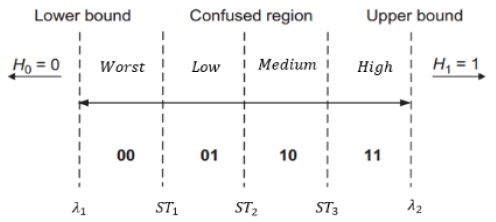
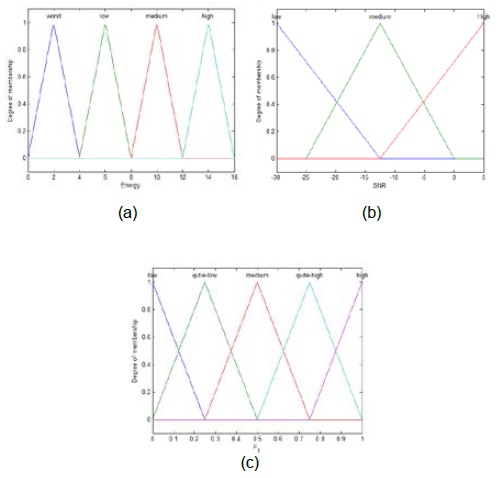
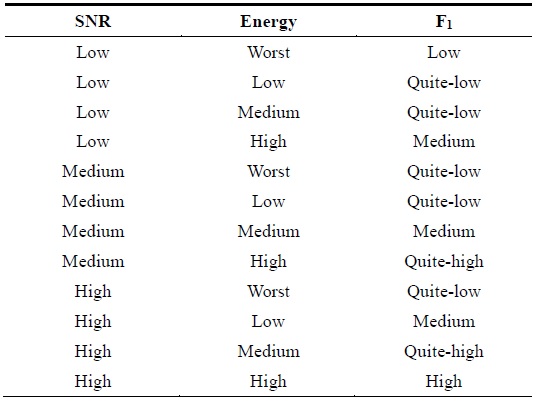
(b) If the energy lies in a confused region, the secondary users will use a fuzzy logic scheme to decide the actual conditions. Inside the FIS, the confused region is divided into four equal regions using two-bit quantization (
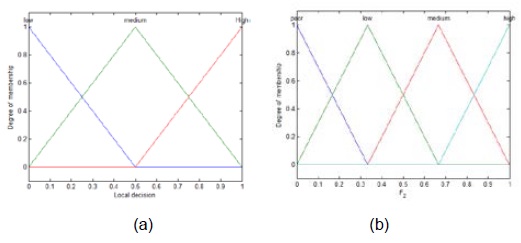
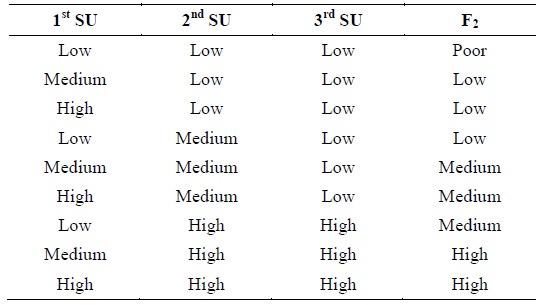
The membership functions (MF) for two-bit quantization, SNR and F1, are shown in Fig. 3. In Table 1, we present the fuzzy rule-based system used for rule evaluation in the first stage.
[Table 1.] Rule-based system for the first stage
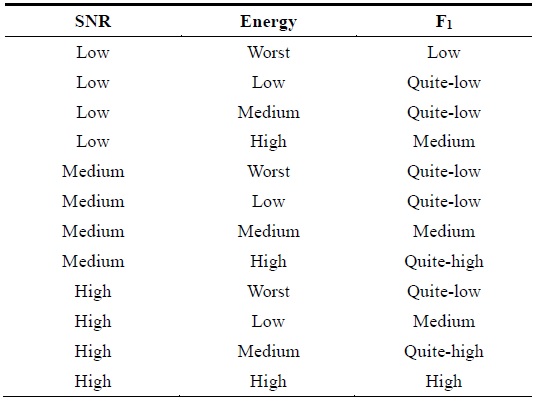
Rule-based system for the first stage
(c) According to the process for FIS in the first stage, shown in Fig. 1, the fuzzifier converts each crisp input value to a linguistic variable using the membership function. The output for the fuzzification process is the fuzzy input values. Using the If-Then type, fuzzy rules convert the fuzzy input to fuzzy output and the defuzzifier converts the degrees of membership of the output linguistic variables (fuzzy output) into numerical values using the centroid of area (COA) as the defuzzification method [14]. The range value of the energy in the membership function is an assumed value because it is recalculated when the measured energy lies in a confused region. A detailed description of the decision making process with the fuzzy logic scheme for the first stage is described as follows:
Also, let x, y be the exact values of X, Y. The first step is to calculate the truth value (
Finally, the membership function μz for the final output of variable Z is calculated by taking the maximum value of the modified membership μ′ of all the conclusion output by referring to Z:
After the implication process, all the values of Z are aggregated by summing all of the values.
(d) After performing local spectrum sensing, each secondary user sends their local decision results (
>
B. Second Stage (Fusion Center)
The fusion center combines all the local decisions using the fuzzy logic scheme. Thus, there are three local decision values as crisp input for the fuzzification process. The next process also uses the same procedure as point (c) in the first stage for the decision combining process. However, for FIS in the second stage, we used the max-product implication method as the implication method and the middle of maximum (MOM) method as the defuzzification method. The defuzzification method for MOM can be expressed as
where is the y-axis value of the local maximum; is the x-axis value of the local maximum point; and
[Table 2.] Example rule-based system for the second stage
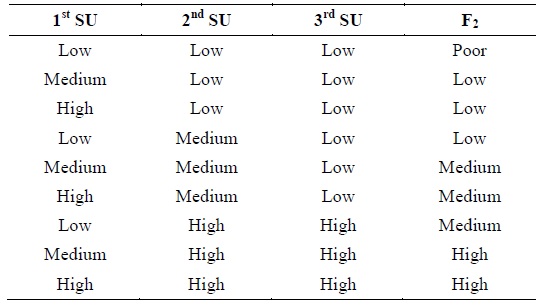
Example rule-based system for the second stage
IV. SIMULATION RESULTS AND ANALYSIS
The simulation was implemented using MATLAB. The parameters used for our simulation were total samples (
The performance results of our proposed scheme were evaluated and compared with other schemes that have a different number of thresholds. These are the CFAR (single threshold) scheme, double adaptive thresholds scheme, and three thresholds scheme. We applied the AND rule and the OR rule as the decision rules in the fusion center. The AND rule decides that a signal is present if all users have detected a signal [16]. The cooperative probability of detection (
In the opposite way, if at least one of the secondary users decides that a primary user signal is present at the local decision, the fusion center decides whether a primary user is present. This fusion rule is known as the OR rule [16]. The cooperative probability of detection (
where
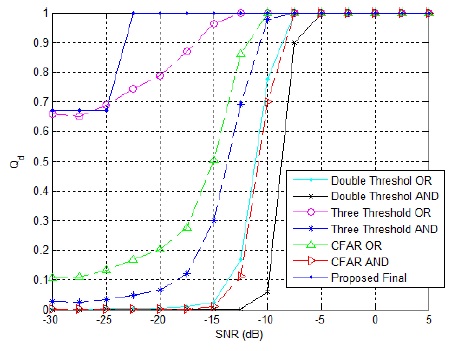
Fig. 5 shows a comparison of the cooperative detection probability as a function of the SNR value. As the SNR value decreases in the local node, the cooperative probability of detection (
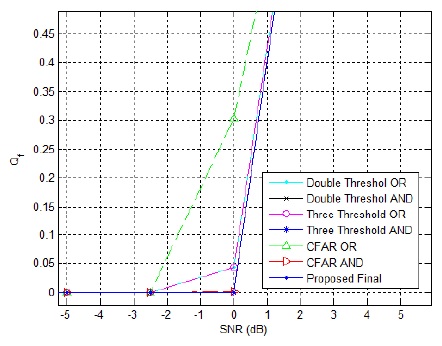
Fig. 6 shows a comparison of the cooperative false alarm probability when the signal is noise only or the primary user is almost absent. Spectrum sensing is performed with a variant of the SNR value or a variant in the noise power. As shown in Fig. 6, the cooperative probability of a false alarm (
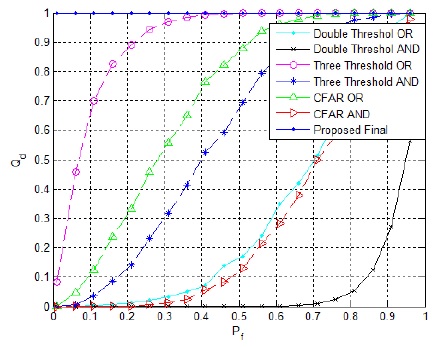
Fig. 7 shows a comparison of the cooperative detection probability (
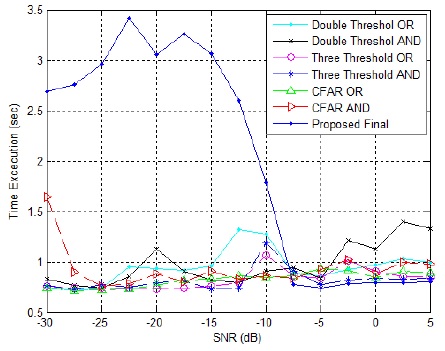
Fig. 8 shows a comparison of the executed time as a function of SNR when a primary user is present. The overall results of the average executed time for determining the channel status are below one second. When a secondary user faces worse SNR, the proposed scheme can enhance the accuracy of detection better than the other schemes. However, when SNR = -30 dB to -15 dB, the proposed scheme requires around three seconds for time execution. This indicates that in order to achieve high accuracy, execution time must be slightly sacrificed.
The aim of this paper is to enhance the performance of spectrum sensing schemes, particularly energy detection. Although our energy detection scheme is simple to implement, it is not robust at low SNR conditions, and the performance of the energy detection is limited by noise uncertainty. Furthermore, multipath fading, shadowing, and the hidden node problem degrade the performance of single-user spectrum-sensing techniques. Thus, a fuzzy logic scheme is applied to enhance the performance of energy detection based on double thresholds as well as to achieve high flexibility for decision making. By using a fuzzy logic scheme, vagueness and unclear decisions are mitigated in a confused region. Based on the simulation results, our scheme successfully enhances the performance of energy detection at low SNR and reduces the effect of noise uncertainty.