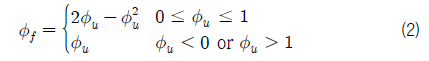높은 정도의 수치 해를 제공하는 직접 수치 모사 (direct numerical simulation, DNS)와 대형 와 모사 (large eddy simulation, LES)는 수치 해석에 필요한 많은 시간과 비용으로 인해 주로 평판, 실린더, 익형 등과 같은 단순한 형상과 낮은 레이놀즈 수를 갖는 유동 해석에 국한되어 왔다. 반면 선체 주위 유동, 복잡한 형상의 선미 부가물 후류 등과 같이 현업에서 발생하는 유동 해석의 경우에는 해의 정도가 낮더라도 수치적 효율성과 안정성을 높이기 위해 상용 프로그램을 이용한 RANS(Reynolds averaged Navier-Stokes simulation) 해석이 주로 활용되었다. 그러나 최근 고성능 전산기가 대형화, 보편화되고 보다 정도 높은 유동 해석이 필요해지면서 현업에서도 LES와 같은 고비용/고정도의 수치 해석에 대한 관심도가 증가하고 있다. 하지만 많은 비용을 들여 현업에서 LES 등을 시도하더라도 상용 프로그램의 제한된 접근성으로 인해 해석 결과에 대한 정도를 보장하기 어려울 뿐만 아니라 소스 코드의 폐쇄성으로 인해 정도를 개선하기도 어렵다.
본 연구에서는 이러한 한계를 극복하기 위해 소스 코드가 완전히 공개된 OpenFOAM을 이용하여 고정도 수치 해석을 수행하였다. OpenFOAM은 유한 체적법을 기반으로 하는 편미분 해석 프로그램이므로 복잡한 형상이나 다양한 격자 형태로 확장이 가능하다. 선체 저항 해석(Lee & Lee, 2014)이나 자유 수면을 고려한 운동 해석(Lee & Kim, 2015)과 같은 기존 연구를 통해 OpenFOAM의 수치적 확장성이나 안정성은 이미 상용 프로그램과 비교 검증되었으나 기존 연구들이 모두 RANS 해석을 통해 수행되었으므로 이제는 DNS나 LES와 같이 고정도 해석 결과에 대한 체계적인 정도 검증이 필요하다. 또한 선체 및 프로펠러 주위 유동에 대한 수치 모사을 위해 다면체의 비정렬 격자(polyhedral unstructured mesh)와 프리즘 층(prism layer)을 사용한 RANS해석(Park et al. 2014)이 많이 수행되고 있는데, 이러한 비정렬 격자 형태가 고정도 수치 해석에 적합한지에 대한 검증도 필요하다. 특히 다양한 형태의 비정렬 격자 중 국소적으로 격자를 밀집 시키기 위해 4분할, 8분할한 quatree, octree 구조의 어댑티드 격자와 벽면 근처 프리즘 층의 조합은 격자 직교성, 효율적인 격자 밀집, 벽면 밀집도 유지를 동시에 달성할 수 있는 격자 구성이므로 벽 함수(wall function)를 사용하는 RANS에서는 매우 유용한 격자 형태이지만, 격자가 합쳐지는 영역에서 국소적으로 격자의 비직교성이 나타나므로 DNS와 같은 고정도 해석에서 어댑티드 격자가 어떤 영향을 미치는지에 대한 검토가 수반되어야 한다. 만일 DNS나 LES에서 어댑티드 격자를 사용하더라도 유동 특성이 변하지 않는다면 RANS에서와 마찬가지로 어댑티드 격자와 프리즘 층의 조합을 이용하여 매우 효율적으로 난류 유동을 고정도 해석할 수 있는 기반이 마련되어질 것이다.
이를 위해 본 연구에서는 OpenFOAM(version 3.0.0)을 이용하여 평판에서 발달하는 난류 경계층에 대한 DNS를 수행하였다. 난류 경계층을 선정한 것은 기존 연구에서 실험이나 수치 해석을 통해 검증된 결과가 많을 뿐만 아니라 단순한 주기적 경계 조건을 통해 난류 천이를 얻을 수 있는 관내 유동과 달리 내부 척도(inner scale), 외부 척도(outer scale) 등을 이용하여 입구 유동을 생성하는 보다 어려운 문제에도 OpenFOAM을 적용할 수 있음을 보이기 위함이다. 또한 저항, 자항, 파랑 하중 해석 등과 같이 조선 해양 분야에서 사용되는 대부분의 문제가 외부 유동이므로 향후 OpenFOAM을 이용한 조선 해양 관련 유동 해석에 대한 기반 지식을 제공하고자 한다. 나아가 어댑티드 격자를 통해 불필요한 부분의 격자를 감소시킴으로써 정렬 직교 격자와 동일한 정도를 유지하면서 보다 효율적으로 고정도 수치 해석 수행이 가능함을 보이고자 한다.
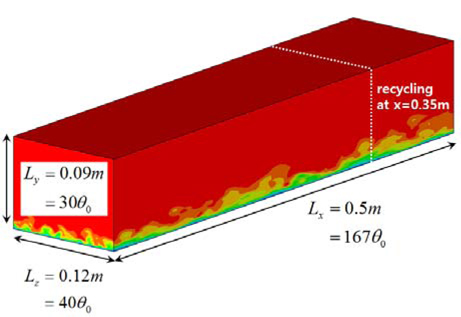
난류 경계층을 수치 모사하기 위해서는 물리적으로 의미있는 벽면 난류 구조를 갖는 유동을 입구 경계 조건으로 부과하여야 한다. 이를 위해 Lund et al.(1998)의 방법에 따라 Fig. 1과 같은 계산 영역에서 x=0.35m의 위치에 있는 속도 성분을 재구성하여 입구 경계 조건으로 부과하였다. 즉 x=0.35m의 위치에서 만들어진 Reθ=345의 난류 경계층을 Reθ=240인 난류 경계층으로 재구성하여 입구 경계 조건으로 부과하였다. 속도 성분은 평균 속도와 변동 속도로 구분하고 내부 척도와 외부 척도에 따라 가중 함수를 사용하는 방법으로 재구성하였다. 자유 유동 속도(free-stream velocity, U∞)는 1m/s이며, 동점도(kinematic viscosity, ν)는 1×105m2/s로 정할 때 입구 경계에서 운동량 두께(momentum thickness, θ)는 0.0024m가 된다. Reθ=300에 해당하는 운동량 두께(θ0)을 기준으로 계산 영역을 무차원화할 경우 계산 영역의 크기는 (167θ0,30θ0, 40θ0)이 된다.
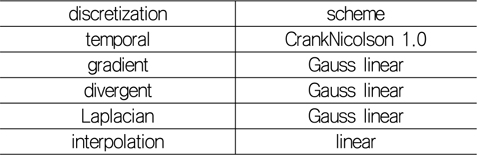
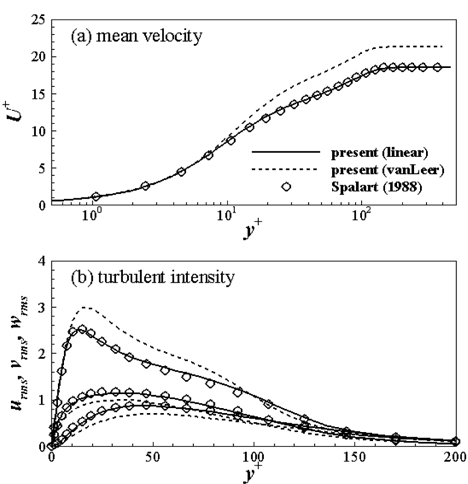
난류 경계층의 직접 수치 모사를 위해 본 연구에서는 PISO(pressure implicit with split operator) 알고리즘에 기반한 pisoFoam을 바탕으로 후류 속도의 재순환(recycling)을 통해 입구 경계 조건을 생성할 수 있는 해석자를 새롭게 구성하였다. 시간에 대한 차분은 2차 정확도를 갖도록 Crank-Nicolson 기법을 사용하였으며, 공간 차분은 Table 1과 같다. 기존 연구에서 유한차분법을 이용하여 평판의 난류 경계층을 해석한 직접 수치 모사의 경우 주로 중앙 차분법(central difference scheme)을 적용한 반면 유한 체적법을 이용하여 LES나 RANS를 수행하는 경우 TVD(total variation diminishing) van Leer 제한자를 갖는 선형차분(이하 vanLeer)이나 normalized variable diagram(NVD) gamma 차분(GammaV), bounded 선형 차분 기법을 사용하였다(Kim et al. 2002, Haren 2011, Freitas 2014). 대류항의 이산화를 위해 OpenFOAM에서 많이 사용하는 vanLeer나 linear-upwind 혼합 차분(linearUpwind) 기법을 사용할 경우 수치적 안정성은 우수하나 격자면에서의 속도에 따라 공간상 1차 정확도가 될 수 있어 평균 속도 분포 및 난류 강도가 부정확해진다. 본 연구에서는 공간상 2차 정확도를 유지할 수 있도록 아래 표와 같이 제한자가 없는 선형 차분(이하 linear)기법을 적용하였다.
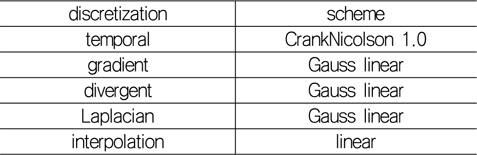
Numerical schemes
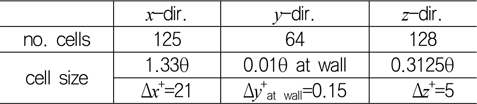
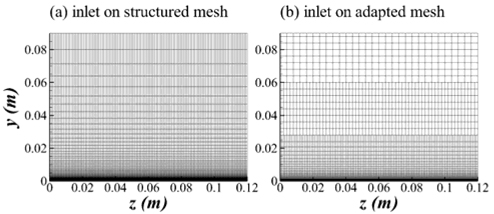
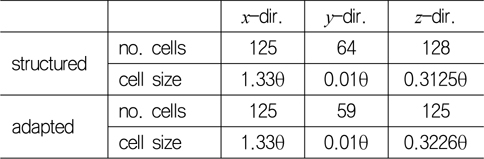
OpenFOAM이 유한 체적법을 사용하므로 비정렬 격자를 활용하는 것도 가능하지만, 입구 경계 조건의 속도 성분을 재구성하기 위해 횡 방향 평균을 사용하기 때문에 정렬 직교 격자로 구성하는 것이 편리하다. 따라서 입구 난류 유동을 생성하기 위한 예비 수치 해석에서는 아래 Table 2와 같은 정렬 직교 격자를 사용하였으며, 생성된 난류 유동을 입구 경계 조건으로 하는 본 수치해석에서는 정렬 직교 격자와 어댑티드 격자에서 얻어진 해석 결과를 비교 분석하였다. Table 2에서 보듯이 주 유동(streamwise,
[Table 2] Grid system for inflow generation
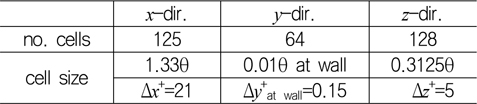
Grid system for inflow generation
입구 경계 조건은
여기서
Reθ=300의 난류 경계층 유동을 입구 경계 조건으로 사용하여 새로운 난류 경계층을 수치 모사하였다. 여기서 사용한 계산 영역의 크기는 입구 난류 유동을 생성할 때 사용한 Fig 1의 영역과 동일하며, 정렬 직교 격자의 경우 입구 난류 유동을 생성할 때와 같은 격자를 사용하였다. 본 연구에서 적용한 정렬 격자의 경우 평판 경계층에서 벽면 난류 구조를 정도 높게 모사하기 위해 기존 연구들에서 많이 사용되었던 격자와 동일한 크기를 갖도록 생성하였다 (Kim et al. 2002, Lee & Sung 2005, Kim & Sung 2006). 즉 주 유동 방향 격자 간격 Δ
정렬 직교 격자가 물리량의 내삽과 구배를 정도 높게 계산하는데 유리한 것은 사실이나 Fig 3(a)에서 보듯이 경계층 바깥 영역(
[Table 3] Comparison of grid system
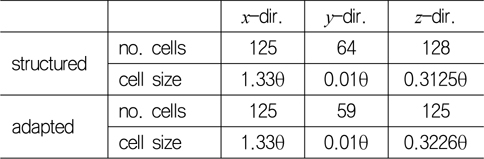
Comparison of grid system
난류 경계층 입구 유동을 사용하여 3초 동안 초기 조건에 의한 과도(transient) 유동을 흘려 보냈다. 난류 구조의 대류 속도를 0.5U∞~0.7U∞로 가정할 경우 입구에서 유입된 난류 구조가 전체 계산 영역을 통과해서 출구로 빠져 나가는데 0.7~1.0초 정도가 소요되므로 3초 동안 초기 조건에 의한 영향이 충분히 제거되었다고 볼 수 있다. 이후 9초 동안 난류 경계층 해석을 수행하면서 필요한 물리량에 대해 횡 방향 및 시간 평균을 취하였다.
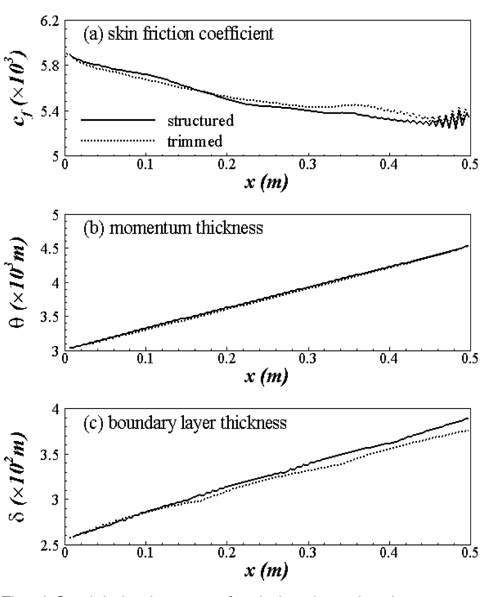
난류 경계층이 발달함에 따라 주 유동 방향으로 표면 마찰 계수(skin friction coefficient,
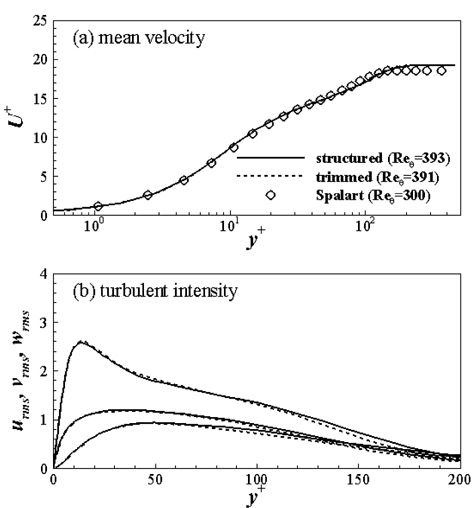
어댑티드 격자에서 해석된 난류 경계층의 유효성을 검증하기 위해 Reθ=391~393에 해당하는
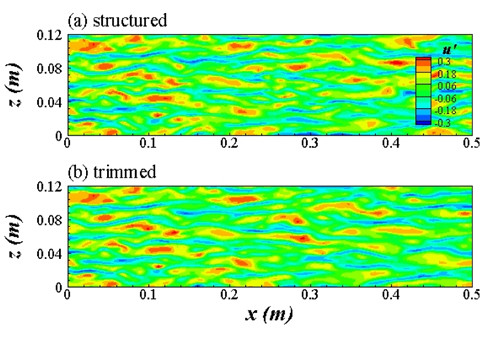
순간 유동장에서 나타나는 난류 유동 특성을 비교하기 위해
지금까지 살펴본 바와 같이 어댑티드 격자와 프리즘 층을 이용하여 정렬 격자와 동일한 특성의 난류 경계층을 매우 효율적 (격자수 40% 감소, 계산 시간 60% 감소)으로 수치 모사할 수 있다. 프리즘 층을 이용한 어댑티드 격자의 각 인자가 난류 경계층의 수치 모사에 미치는 영향을 분석하기에 앞서 먼저 아래와 같은 격자 구성의 전제 조건을 설정하였다.
a. 벽면 첫 번째 격자 크기는 Δy+at wall<0.2를 만족함 b. 벽면 근처 횡 방향 격자 크기는 Δz+=5를 유지함 c. 벽면 근처 주 유동 방향 격자 크기는 Δx+≈20을 유지함
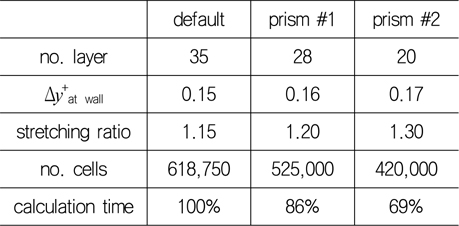
상기 전제 조건을 통해 먼저 프리즘 층의 연신률을 1.15부터 1.3까지 변화시키면서 격자를 생성하여 난류 경계층을 수치 모사하였다. Table 4에서 ‘default’는 앞서 정렬 직교 격자와 비교한 어댑티드 격자에서 기 적용한 프리즘 층이며, ‘prism #1’과 ‘prism #2’에서는 벽면 격자 크기와 프리즘 층의 마지막 격자 크기를 고려하여 연신률과 프리즘 층의 두께를 변화시켰다. 프리즘층 바깥 영역은 Δ
[Table 4] Parameters of prism layer
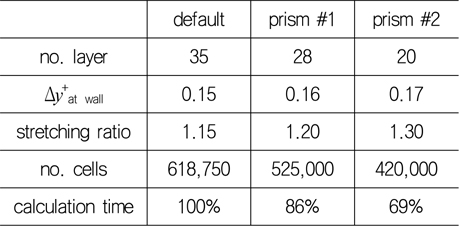
Parameters of prism layer
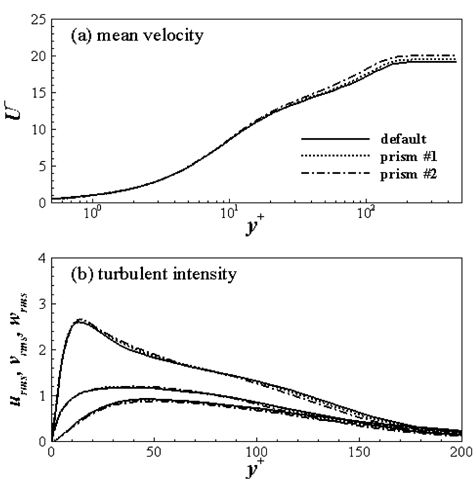
각 격자에 대해
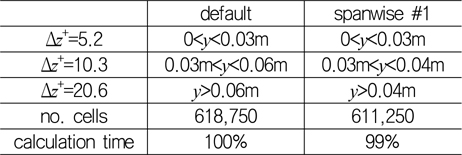
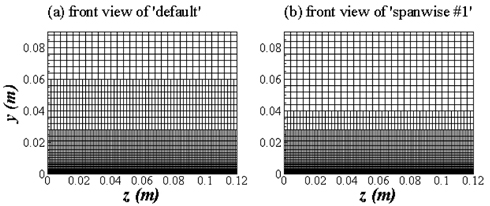
횡 방향 격자 간격에 따른 구간을 Table 5와 같이 서로 다르게 설정하여 난류 경계층을 수치 모사하였다. ‘default’는 앞서 정렬 직교 격자와 비교한 어댑티드 격자에서 적용한 횡 방향 격자 구성이며, ‘spanwise #1’은 Fig에서 보는 바와 같이 보다 빠르게 횡 방향 격자 간격을 증가시킴으로써 전체 격자수를 감소시키기 위한 어댑티드 격자 구성이다. 그러나 경계층 바깥 영역은 횡 방향 격자가 이미 성긴 구간이므로 전체 격자수에서 큰 감소 효과는 기대하기 어렵다. 따라서 난류 경계층 모사에 소요되는 전체 계산 시간 역시 거의 동일하였다.
[Table 5] Spanwise refinement of adapted mesh
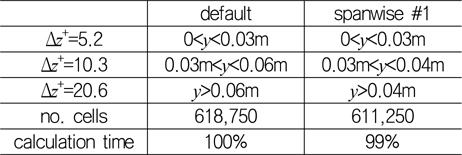
Spanwise refinement of adapted mesh
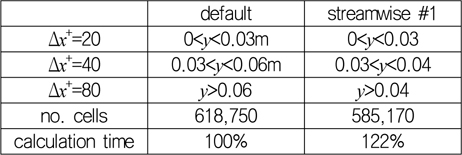
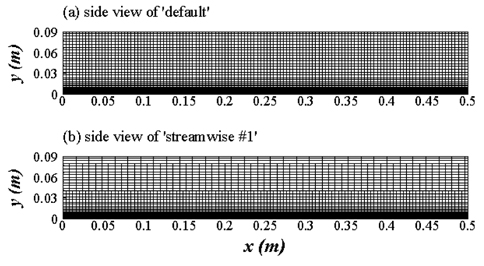
유사하게 주 유동 방향 격자 간격에 따른 구간을 Table 6과 같이 서로 다르게 설정하여 난류 경계층을 수치 모사하였다. ‘streamwise #1’은 Fig. 9에서 보는 바와 같이 경계층 바깥 영역에서 주 유동 방향 방향 격자 간격을 증가시킴으로써 전체 격자수를 감소시키기 위한 어댑티드 격자 구성이지만 횡 방향 밀집도 변화와 마찬가지로 전체 격자수가 크게 감소하지는 않는다. 격자수가 감소하였음에도 불구하고 수치 모사에 소요되는 계산 시간은 오히려 20% 이상 증가하였는데, 이는 각 계산 시간 단계에서 압력의 잔여 오차를 감소시키는데 필요한 반복 계산이 평균 12회에서 소요되는 30회로 증가하였기 때문이다. 프리즘 층이나 횡방향 격자 간격을 증가시켰을 때와 달리 주 유동 방향의 격자 간 격을 증가시켰을 때 V-cycle을 이용한 다중 격자 해석의 수렴 속도가 악화되는 원인은 잔여 오차의 파장별 수렴 속도 분석 등을 통해 향후 체계적으로 밝혀져야 할 부분이다.
[Table 6] Streamwise refinement of adapted mesh
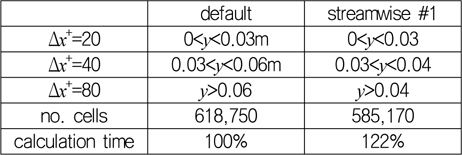
Streamwise refinement of adapted mesh
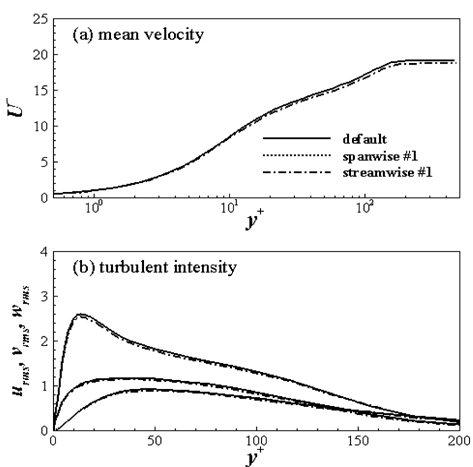
각 격자에서 얻어진 난류 경계층의 통계적 특성은 Fig. 10과 같다. 그림에서 보는 바와 같이 ‘spanwise #1’에서는 ‘default’와 동일한 벽면 마찰 속도, 평균 속도, 난류 강도를 얻을 수 있는 반면, ‘streamwise #1’에서는 마찰 속도가 2.5% 높게 나타났다.
본 연구에서는 OpenFOAM과 어댑티드 격자를 이용하여 난류 경계층에 대한 효율적인 고정도 수치 모사가 가능함을 보였다. Reθ=300의 난류 경계층을 입구 유동 조건으로 하여 주 유동 방향에 대한 표면 마찰 계수, 운동량 및 경계층 두께 변화 등을 비교하였으며, Reθ=390에서 평균 속도 분포, 난류 강도를 비교 분석하였다. 어댑티드 격자와 프리즘 층을 이용할 경우 기존 정렬 직교 격자에 비해 절반 정도의 격자를 사용하더라도 동일한 난류 경계층을 수치 모사할 수 있었다. 또한 어댑티드 격자를 통해 경계층 바깥 영역에서 횡 방향 격자 간격을 증가시킴에 따라 각 계산 단계에서 동일한 압력 잔여 오차를 얻는데 필요한 반복 계산 횟수가 감소함으로써 계산 속도 개선 효과도 매우 높음을 확인할 수 있다. 프리즘 층의 연신률을 증가시킬수록 전체 격자수도 감소하지만 벽면 마찰 속도의 오차 역시 커지게 되므로 정밀한 수치 해를 얻기 위해서는 1.2 이하의 연신률을 사용하는 것이 바람직하다. 경계층 바깥 영역에서 횡 방향 격자 밀집도나 주 유동방향 격자 밀집도를 변화시키더라도 전체 격자수를 감소시키는 효과는 미미하였다. 다만 프리즘 층이나 횡 방향 격자 간격을 증가시켰을 때와 달리 주 유동 방향의 격자 간격을 증가시켰을 때 다중 격자 해석의 수렴 속도가 악화되는 원인은 향후 체계적으로 밝혀져야 할 것이다.