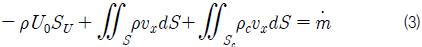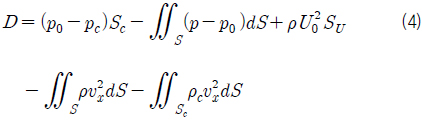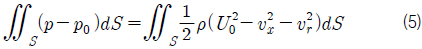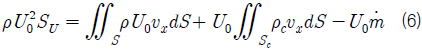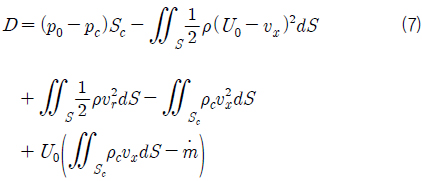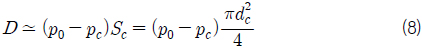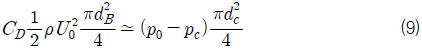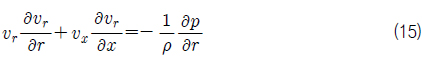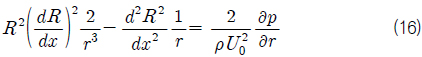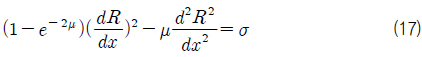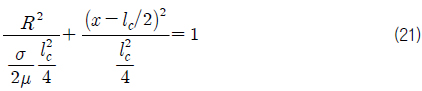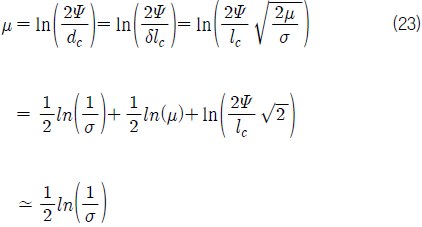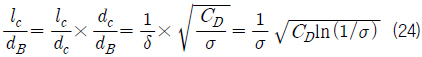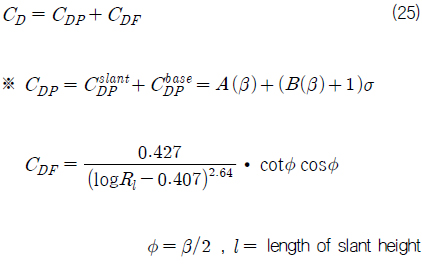A comparative method is applied to evaluate well-known formulas for estimating the size of supercavities of axisymmetric cavitators for the supercavitating underwater vehicle. Basic functional forms of these formulas are derived first for the cavity diameter from a momentum integral estimate and second for the cavity length from an asymptotic analysis of inviscid supercavity flows. The length and the diameter of axisymmetric supercavities estimated by each formula are compared, with available experimental data for a disk and a 45° conical cavitators, and also with computational results obtained by a CFD code, ‘fluent’, for conical cavitators of wide range of cone angles. Results for estimating the length and the diameter of the supercavities show in general a good agreement, which confirms the size of the supercavities for disk and conical cavitators can be estimated accurately by these simple formulas of an elementary function of cavitation number and drag coefficient of the cavitator. These formulas will be useful for from conceptual design of the cavitator to real-time control of the supercavitating underwater vehicle.
수중 운동체의 머리에 장착한 캐비테이터(cavitator)에서 발생시킨 초공동(supercavity)으로 몸체를 감싸서 물과 접촉하는 면적을 최소화시켜 항력을 줄임으로써 수중에서 고속으로 운항하는 기술이 러시아, 미국, 독일 등을 중심으로 연구, 개발되어 왔다. 대표적 사례로 초공동 어뢰(supercavitating torpedo)인 러시아의 Shkval과 독일의 Barracuda를 들 수 있으며, Shkval은 원판 (disk) 형상, Barracuda는 원뿔(cone) 형상의 캐비테이터를 어뢰의 머리에 장착하며 전자는 200노트, 후자는 400노트 이상으로 운항이 가능한 것으로 알려져 있다 (Kim & Nah, 2011).
캐비테이터는 초공동 고속운항기술의 핵심 장치로서 초공동 수중 운동체의 목표 속도를 달성하기 위해서는 몸체를 충분히 감쌀수 있는 초공동을 발생, 유지시켜서 수중운동체의 항력이 최소화 되도록 캐비테이터를 설계하는 것이 필수적이다. 이를 위해서는 수중운동체의 운항속도 및 수심 등의 설계 조건 하에서 캐비테이터의 제원 및 형상에 따른 초공동 크기와 캐비테이터 항력의 변화를 정확하게 추정하여 요구되는 초공동의 길이와 직경을 만족하도록 캐비테이터를 설계하는 도구(design tools)가 필요하다.
현재까지 캐비테이터의 대표적인 형상으로는 원판 또는 원뿔이 채택되어 있는데, 원판과 원뿔에서 발생하는 초공동 및 항력에 대한 공개된 실험 데이터는 (Reichardt, 1946; Eisenberg & Pond, 1948; Self & Ripken, 1955) 오래되었고 원뿔의 경우는 극히 한정된 원뿔 각으로 제한되어 있다. 냉전 이후에는 러시아 연구결과와 (Epshtein, 1973; Logvinovich, 1973; Semenenko, 2001; Savchenko, 2002) 미국의 연구결과에 (Brennen, 1969; Kirschner et al.. 1995; Kunz et al., 2001; Alyanak, et al., 2004) 축대칭 캐비테이터에 대한 초공동 및 항력에 대한 기초적인 정보가 공개되어 있다.
최근, 국내에서 초공동 수중운동체에 대한 연구가 (Ahn, et al., 2010; Ahn, et al., 2012; Kim, et al., 2013; Lee, et al., 2013; Park, 2013; Kim & Lee, 2014; Kim, et al., 2015) 활발히 진행되어 캐비테이터의 초공동 및 항력 특성을 해석할 수 있게 되었고, 이러한 해석기술을 캐비테이터 설계에 활용하려는 시도가 진행되고 있다. 하지만 아직은 캐비테이터 설계에 믿고 활용할 수 있을 만큼 초공동 및 항력 정보가 충분하지 못하기 때문에 이를 보완하기 위한 실험 데이터 그리고 해석 및 추정기술의 신뢰성 확보가 필요하다. 특히 캐비테이터의 초기설계 또는 초공동 수중 운동체의 제어로직 개발을 위해서는 캐비테이터의 제원과 형상에 따른 초공동 크기 및 항력의 변화를 추정하는 간편한 근사식이나 경험식이 보다 더 유용하고 효과적이다.
본 연구에서는 원판과 원뿔 캐비테이터에 대한 캐비테이션 실험과 CFD 유동해석의 초공동 길이 및 직경 자료를 검증기준으로해서 축대칭 캐비테이터에서 발생하는 초공동의 길이 및 직경을 제대로 추정하는 것으로 알려진 3개의 근사식을 (Garabedian, 1956; Logvinovich, 1973; Guzevsky, 1983) 비교 검토하였다. 이를 통해서 캐비테이터의 초기설계로부터 초공동 수중 운동체의 제어로직 개발에까지 활용 가능한 초공동 길이 및 직경 추정식을 조사하였다.
본 장에서는 원뿔 캐비테이터를 대상으로 캐비테이터 제원과 초공동 형상을 정의하고 축대칭 초공동의 길이 및 직경을 추정하는 기존 근사식들의 함수적 기본 특성을 살펴보았다.
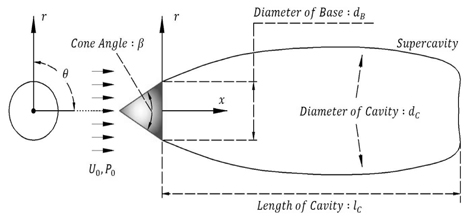
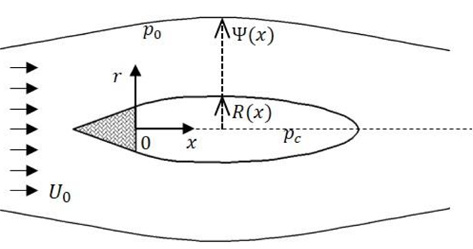
좌표계는 Fig. 1과 같이 캐비테이터 베이스의 중심을 원점으로 잡고 균일류
캐비테이션 수는 식 (1)과 같이 정의하고 항력계수는 식 (2)와 같이 항력을 정체압력과 베이스 면적의 곱으로 나누어 무차원화 하였다.
2.2.1 초공동 직경 추정 근사식
중력을 무시할 수 있고 캐비테이션 수가 충분히 작다고(통상
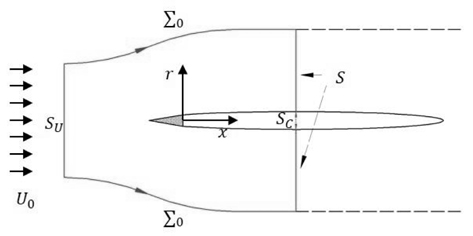
Fig. 2의 제어체적에 대한 질량보존법칙은 다음과 같은 식으로 나타낼 수 있다.
동일한 제어체적의
베르누이 방정식을 이용하여 우변의 두 번째 항을 다음과 같이 치환할 수 있다
또 우변의 세 번째 항은 식 (3)을 이용하여 다음과 같이 바꾸어 나타낼 수 있다.
식 (5)와 (6)을 식 (4)에 대입하고 정리하면 항력은 식 (7)과 같이 나타낼 수 있다.
공동 단면
이 식은 캐비테이터의 항력이 기준압력과 캐비티 압력의 차에 비례하고 초공동 직경의 제곱에 비례함을 보여준다. 항력계수가 식 (2)와 같이 정의됨을 고려하면 식 (8)은 다음과 같이 다시 쓸 수 있다.
식 (9)를 초공동 직경과 캐비테이터 직경의 비에 대한 관계식으로 정리하고 캐비테이션 수의 정의 식 (1)을 사용하여 나타내면 다음과 같은 근사식을 얻을 수 있다.
이 식으로부터 초공동의 직경이 캐비테이터 직경과 항력계수의 거듭제곱근에 비례하고, 캐비테이션 수의 제곱근에 반비례하며, 원뿔 각과 같은 캐비테이터 형상의 영향은 항력계수에 포함되어 나타남을 알 수 있다.
2.2.2 초공동 길이 추정 근사식
축대칭 초공동의 길이는 긴 회전 타원체 형상의 초공동 주위 비점성 축대칭 유동에 대한 점근 근사 해석을 통해 캐비테이터 직경, 캐비테이션 수 그리고 캐비테이터 항력계수의 함수로 근사하여 나타낼 수 있다. 이하는 7번째 참고문헌의 내용을 (Franc & Michel, 2004 pp.117~121) 간추려 소개한 것임을 밝혀둔다.
액체유동의 속도가 반경 및 축 방향 속도 성분만 있고 접선 방향 성분은 없다고 가정하면 연속 방정식은 다음과 같다.
세장체 이론에 의하면 캐비테이터 및 초공동 주위 액체유동의 축 방향 유속
공동 경계면
식 (12)의
식 (14)의 관계를 다음의 반경 방향 Euler 방정식에 대입하고,
축 방향 유속
Fig. 3과 같이 공동으로부터 멀리 떨어진 반경
여기서 식 (17)의 변수
또, 초공동의 세장비
변수
이제 초공동의 양쪽 끝
따라서 초공동의 세장비
또 상수
식 (22)와 (23) 그리고 식 (10)으로부터 초공동 길이와 캐비테이터 직경의 비를 캐비테이션 수와 캐비테이터 항력계수의 함수로 근사하여 다음과 같이 나타낼 수 있다.
이 식은 초공동의 길이가 캐비테이터 직경과 항력계수의 거듭제곱근에 비례하고 캐비테이션 수의 멱함수에 반비례하는 함수적 특성을 보여준다.
2.2.3 초공동 크기 추정식 비교
초공동 크기의 추정에는 세장체 이론을 기반으로 한 점근 근사식(Garabedian, 1956)과 포텐셜 유동의 수치해 및 실험자료를 사용해서 보정한 2개의 준 경험식(Logvinovich, 1973; Guzevsky, 1983)이 널리 사용되고 있다. Table 1은 축대칭 초공동의 길이와 직경을 추정하는 이 식들을 비교하여 보여준다.
[Table 1] Formulas for estimating supercavity sizes
Formulas for estimating supercavity sizes
Table 1의 식들은 모두 식 (10) 및 (24)와 함수적 기본 특성이 동일하며, Guzevsky (1983)의 경우만 초공동 길이 추정 시 원뿔 각에 따라서 약 10% 이내의 추가적인 보정을 하고 있다. 한편, Table 2는 각각의 식에 사용된 항력계수(
[Table 2] Drag coefficients of cones for zero cavitation number
Drag coefficients of cones for zero cavitation number
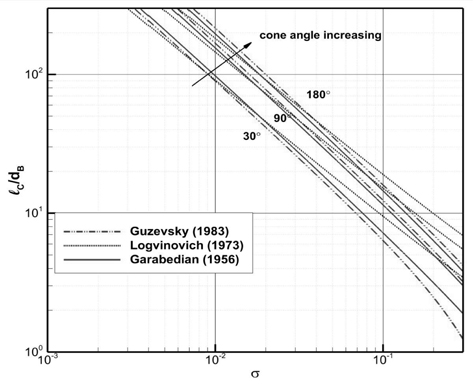
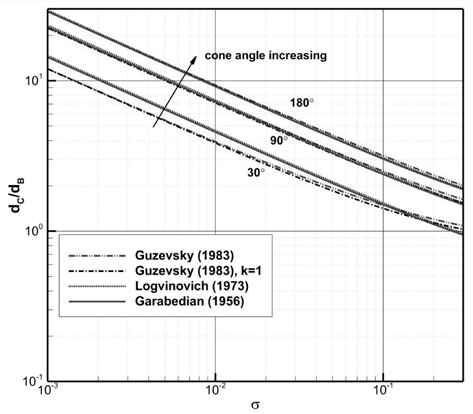
원뿔 각 180° (원판), 90° , 30° 인 캐비테이터에 대해서 Table 1의 3가지 근사식을 사용하여 추정한 초공동 길이와 직경을 비교한 결과를 각각 Fig. 4와 Fig. 5에 나타내었다.
Logvinovich (1973) 추정식의 초공동 길이가 다른 두 추정치와 크게 차이나는 것은 주로
캐비테이션 수가 큰 영역에서 추정치의 차이가 더 크며, 특히 Logvinovich 근사식이 초공동의 길이를 과도하게 크게 추정한다. 원뿔 각 30° 의 경우, 캐비테이션 수가 클수록 Guzevsky (1983)의 근사식이 초공동 길이를 더 작게 추정하는 것은 원뿔 각에 따른 추가적인 보정 때문이다.
초공동 직경은, 원뿔 각 180° (원판), 90° 의 경우, 3개 근사식의 차이가 거의 없는 반면에, 원뿔 각 30° 의 경우에는 유독 Guzevsky 근사식으로부터 추정된 초공동 직경만 다른 추정치와 큰 차이를 보인다. 그 원인을 알아보기 위해서 원뿔 각 30° 에 대해 보정계수
앞서 Table 2에 정리한 축대칭 캐비테이터의 항력계수의 추정식은 세장체 유동이론에 기초한 점근 근사식 또는 포텐셜 유동의 수치해나 실험 자료를 사용하여 보정한 준 경험식이다. 최근에는 CFD 코드 (fluent)를 사용해서 계산한 초공동 난류유동의 수치해석 결과로부터 원뿔 캐비테이터의 항력계수를 추정하는 새로운 공식이 제안된 바 있다 (Kim et al., 2015).
원뿔 캐비테이터의 항력은 경사면(slant surface)과 베이스면(base surface)에 작용하는 압력항력과 경사면에 작용하는 마찰항력의 합으로서 식 (25)와 같이 표현할 수 있다.
※ Two regions in accordance with
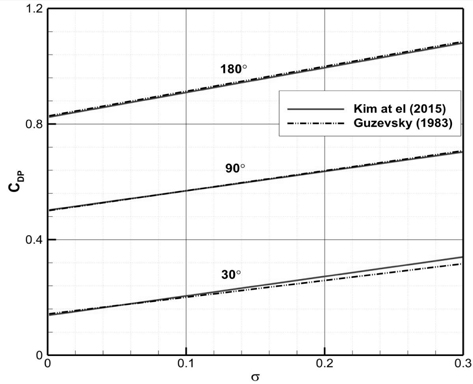
Fig. 6는 원뿔 각 180° (원판), 90° , 30° 인 캐비테이터의 압력항력계수를 Kim et al. (2015)과 Guzevsky (1983)의 근사식으로 추정하여 비교한 결과를 보여준다.
원뿔 각 180° 와 90° 의 경우 Kim et al. (2015)의 항력계수와 Guzevsky (1983)의 항력계수가 거의 동일하게 나타난다. 원뿔 각 30° 의 경우에는 전자가 후자보다 다소 크며, 캐비테이션 수가 큰 영역에서 그 차이가 조금 더 커진다.
실험 데이터가 있는 원뿔 각 180° 및 45° 캐비테이터를 대상으로 Kim et al. (2015)의 항력계수 추정식과 Garabedian (1956)의 근사식을 사용하여 추정한 초공동의 길이와 직경의 타당성을 검증하였다.
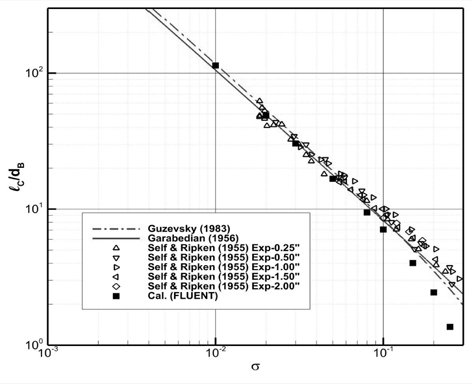
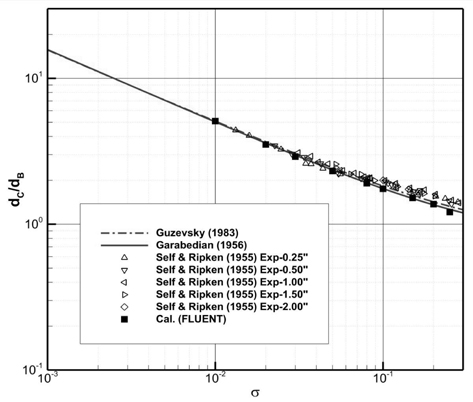
먼저 원뿔 각 45° 에 대해 새로운 항력계수로 추정한 초공동 길이와 직경을, 각각 Fig. 7과 Fig. 8에, Self and Ripken (1955)의 실험 데이터, Guzevsky (1983)의 근사식 추정치 그리고 Kim et al. ( 2015)의 CFD 코드 (fluent) 유동해석 결과와 함께 비교하여 나타내었다.
Kim et al. (2015)의 항력계수를 사용하면 Garabedian (1956) 근사식으로 추정한 초공동 길이가 Guzevsky (1983)근사식의 길이와 유사하며, 캐비테이션 수가 0.1 보다 작은 영역에서는 Guzevsky (1983) 보다 다소 작게 추정하고, 0.1 보다 큰 영역에서는 다소 크게 추정한다.
캐비테이션 수 0.01 ≤
직경의 경우, 캐비테이션 수의 영역 전반에 걸쳐 Garabedian (1956)과 Guzevsky (1983) 근사식의 직경 차는 길이 차에 비해 근소하며, 두 근사식 모두 실험 데이터 및 CFD 결과와 잘 일치하는 추정결과를 주고 있다. 캐비테이션 수가 클수록 Garabedian (1956) 근사식이 Guzevsky (1983) 근사식에 비해 직경을 조금 더 작게 추정하는 경향이 있으며, 캐비테이션 수가 0.1 이상인 영역에서 두 근사식 모두 실험결과 보다 초공동 직경을 다소 작게 추정한다.
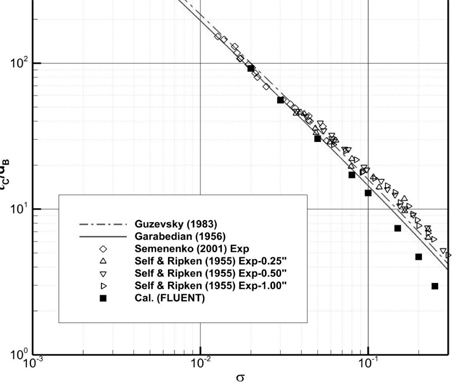
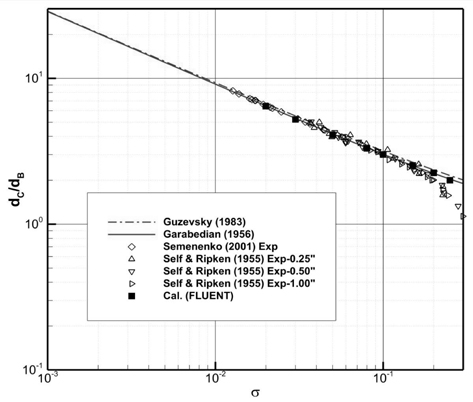
동일한 방법으로 원뿔 각 180° (원판)에 대해 캐비티 길이 (Fig. 9) 및 직경(Fig. 10)의 추정결과를 살펴보았다. Fig. 9에 보인 바와 같이 Garabedian (1956)과 Guzevsky (1983) 근사식으로 추정한 초공동 길이는 유사하며, 전자가 후자보다 약 9% 정도 초공동 길이를 작게 추정한다. 캐비테이션 수 0.01 ≤
원뿔 각 45° 의 경우와 마찬가지로 Garabedian (1956)과 Guzevsky (1983)의 근사식으로 추정한 원뿔 각 180° (원판)의 캐비티 직경은 캐비테이션 수의 영역 전반에 걸쳐 거의 차이가 없고, 두 근사식 모두 실험결과 및 CFD 해석결과와 잘 일치하는 결과를 주고 있다. 캐비테이션 수가 클수록 Garabedian (1956) 근사식이 Guzevsky (1983) 근사식에 비해 초공동 직경을 조금 더 작게 추정하는 경향이 나타나며, 캐비테이션 수가 0.2 보다 큰 영역에서는 초공동 직경의 계측치가 급격하게 줄어듦으로서 근사식 및 CFD 결과와 조금 더 큰 차이를 보인다.
이상의 비교, 분석 및 검토 결과로부터 축대칭 초공동의 길이 및 직경을 추정하는 Garabedian (1956)과 Guzevsky (1983)의 근사식이 타당함을 확인하였다.
다음 절에서는 Garabedian (1956)의 근사식을 선택해서 다양한 원뿔 각의 캐비테이터에서 발생하는 초공동 길이 및 직경을 추정하고 그 결과를 분석하여 원뿔 각이 초공동 크기에 미치는 영향을 조사하였다.
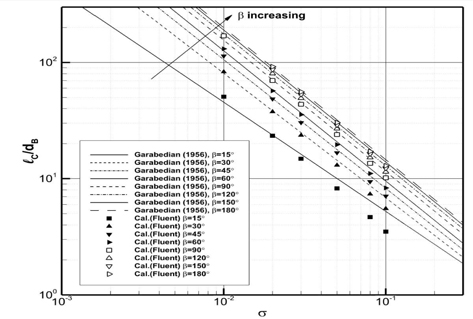
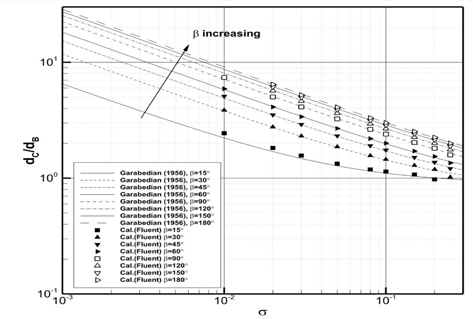
원뿔 각이 15° ∼ 180° 범위에서 서로 다른 8개의 캐비테이터에 대해 Kim et al. (2015)의 항력계수와 Garabedian (1956)의 근사식을 사용하여 초공동의 길이 (Fig. 11) 및 직경 (Fig. 12)을 추정하고 캐비테이션 수 0.01 ≤
Fig. 11에 보인 바와 같이 근사식을 사용하여 추정한 초공동의 길이는 CFD 해석결과와 근사하지만 캐비테이션 수가 클수록 CFD 해석결과에 비해 길고 따라서 캐비테이션 수 증가에 따른 초공동 길이의 감소율이 다소 작으며 이러한 경향은 원뿔 각이 작을수록 더 심화된다. 동일한 캐비테이션 수에서 원뿔 각이 작을수록 캐비테이터 단위직경 당 초공동의 길이가 짧아지는 것은 CFD 해석결과와 유사하지만 캐비테이션 수가 클수록, 특히 원뿔 각이 가장 작을때, 단위직경 당 초공동 길이를 크게 추정하는 경향을 나타낸다.
Fig. 12는 근사식으로부터 추정한 초공동의 직경이 CFD 해석결과와 전반적으로 잘 일치하는 것을 보여준다. 원뿔 각이 작아질수록 캐비테이터 단위직경 당 초공동 직경이 줄어들고 캐비테이션 수가 클수록 초공동 직경의 감소율이 작아지는 특성도 일치하고 있다. 원뿔 각이 60° 이상인 경우, CFD 해석결과에 비해 초공동 직경을 조금 크게 추정하는 경향을 보이는 반면에, 원뿔각이 45° 이하인 경우에는 초공동의 직경을 CFD 해석결과에 비해 다소 작게 추정하는 것으로 나타난다.
원뿔 각이 15° ∼ 180° 범위에서 서로 다른 8개의 원뿔 캐비테이터를 대상으로 Kim et al. (2015)의 항력계수와 Garabedian (1956)의 근사식으로 초공동 길이 및 직경을 추정한 결과, 원뿔 캐비테이터에서 발생하는 초공동 길이와 직경 추정식의 적합성을 확인하였으며 초공동 수중운동체의 초기 설계 단계에 캐비테이터 기본형상과 제원을 선정함에 있어 유용한 결과를 제공할 것으로 판단된다.
원판과 원뿔 캐비테이터에 대한 초공동 길이 및 직경 자료를 검증기준으로해서 축대칭 캐비테이터에서 발생하는 초공동 길이 및 직경을 제대로 추정하는 것으로 널리 알려진 3개의 근사식을 (Garabedian, 1956; Logvinovich, 1973; Guzevsky, 1983) 비교 검토하였다.
축대칭 초공동 유동에 대한 운동량적분해석과 세장체 유동이론 기반의 점근근사해석을 통하여 축대칭 초공동의 길이 및 직경을 추정하는 근사식의 함수적 특성을 살펴보았다. 그 결과, 초공동의 길이와 직경이 캐비테이터 직경과 항력계수의 거듭제곱근에 비례하고 캐비테이션 수의 멱함수에 반비례함을 확인하였다.
원뿔 각 180° (원판), 90° , 30° 인 캐비테이터에 대해 상기 3개 근사식을 사용하여 추정한 초공동 길이와 직경을 비교한 결과, 추정치가 큰 차이를 나타낸 것은 주로 각 근사식에 사용된 항력계수 때문이며 보정계수의 영향은 비교적 작음을 확인하였다. Logvinovich (1973)의 근사식은 캐비테이션 수에 대한 함수적 특성을 제대로 반영하지 않아서 초공동의 길이를 추정하는데 부적합함을 확인하였다.
실험 데이터가 있는 원뿔 각 180°및 45°캐비테이터를 대상으로 Kim et al. (2015)의 항력계수 추정식과 Garabedian (1956)의 근사식을 사용하여 추정한 초공동의 길이와 직경을 비교 연구한 결과, Garabedian (1956)과 Guzevsky (1983)의 근사식이 모두 타당함을 확인하였다.
원뿔 각이 15° ∼ 180° 범위에서 서로 다른 8개의 캐비테이터에 대해 Kim et al. (2015)의 항력계수와 Garabedian (1956)의 근사식을 사용하여 초공동의 길이 및 직경을 추정한 결과, 원뿔 각에 따른 초공동의 길이와 직경의 변화를 제대로 추정하였으며, 따라서 본 연구를 통해 검증된 초공동 크기 추정식은 캐비테이터의 형상 설계와 초공동 수중 운동체의 제어로직 개발 등에 유용하게 사용할 수 있을 것으로 판단된다.
