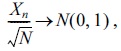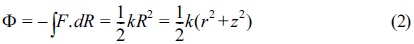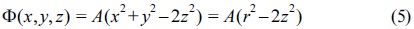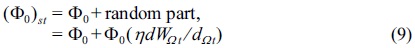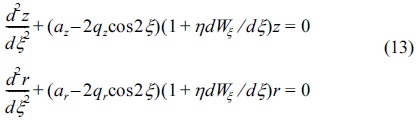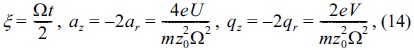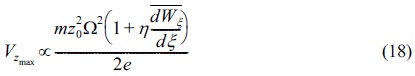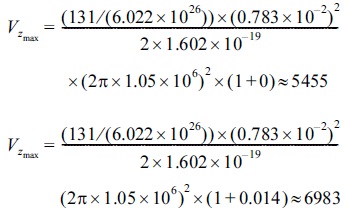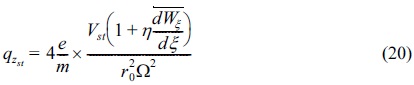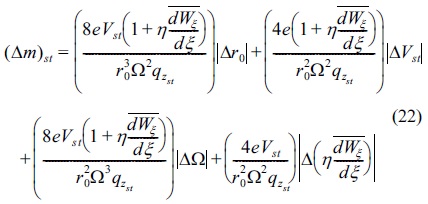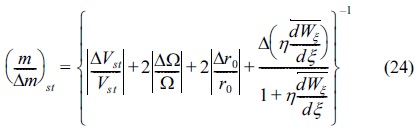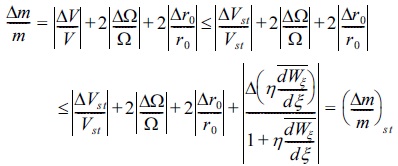There is the possibility that an ion trap mass spectrometer incorporates such traps as the Penning,1 Paul2 or Kingdon3 traps. In 2005, the Orbitrap was introduced according to the Kingdon trap.4 The two most popular kinds of ion traps are the Penning and the Paul traps (quadrupole ion trap).5-8 Of course, it is also possible that other kinds of mass spectrometers utilize a linear quadrupole ion trap selected as a mass filter. Interestingly, ion trap mass spectrometry has undergone many developmental stages in order to achieve its current condition with relatively high performance level and growing popularity. Paul and Steinwedel9 invented Quadrupole ion trap (QIT) commonly used in mass spectrometry,5-8 ion cooling and spectroscopy,10 frequency standards,11 quantum computing12 and others. However, different geometries have also been suggested and utilized for QIT.13

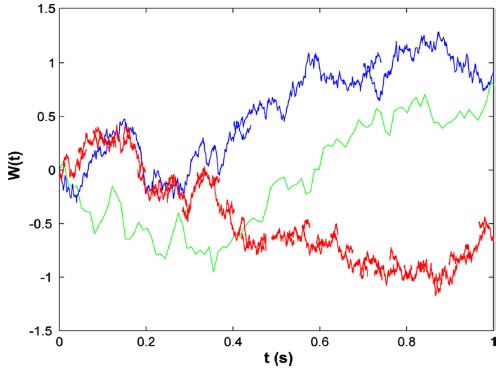
A Wiener process14,15 (notation W=(W_t)_t≥0)) is named in the honor of Prof. Norbert Wiener; other name is the Brownian motion (notation B=(B_t)_t≥0)). Wiener process is Gaussian process. As any Gaussian process, Wiener process is completely described by its expectation and correlation functions14,15

Main properties of W=(W_t)_t≥0) :

• W₀ = 0

• Trajectories of Wiener process are continues functions of t ∈ [0, ∞] (see Figure (1)),

• expectation E[W_t]=0,

• correlation function E[W_tW_s]=min(t,s),

• for any t₁, t₂,…t_n the random vector (W_t1, W_t2,…W_tn) is Gaussian,

• for any s, t

• Increments of Wiener process on non overlapping intervals are independent, i.e. for (s₁, t₁)∩(s₂, t₂)=0 the random variables W_t2-W_s2, W_t1-W_s1 are independent,

• paths of Wiener process are not differentiable functions,

• martingale property,

Consider a simple random walk X_n∈N on the lattice of integers Z,

where {ξ_k}_k∈N is a collection of independent, identically distributed random variables with P(ξ_k=±1)=1/2. From the Central Limit Theorem16,17 we have,

in distribution as N→∞. Here N(0, 1)is the Gaussian variable with mean 0 and variance 1. This suggests to define the piecewise constant random function on t∈[0, ∞] by letting,

In can be shown that as N→∞, converges in distribution to a stochastic process W_t, termed the Wiener process or Brownian motion.14-17

Fig. (2) shows indicatesa the schematic perspectives of a quadrupole ion trap (QIT). The quadrupole ion trap is the ion trap which including hyperbolic geometry and also is composed of involves a ring and two end cap electrodes that facing face each other in the z-axis (see Fig. (2)). Here, z₀ can also be considered the distance that begins started from the center of the QIT to the end cap. Also, r₀ is regarded as the distance from the outset point in the center of the QIT and extends to the nearest ring surface. Forcing the particles to swing and vibrate in confined space6,18-20 can be the best approach for trapping charged particles. Such force can be written as follows,

Where R is regarded as the distance from the center of the swing to the particle position and k is seen as a constant. Such force generated via the parabolic potential will move the oscillating particle around the equilibrium point. It can be expressed as follows,

Here, R²=r²+z², r²=x²+y². Also, x,y,z can be considered as Cartesian space components. Furthermore, any possible free space should satisfy the Laplace equation, given as follows,

As Eq. (2) is unable to satisfy the Laplace situation, thus for confining the ions in two dimensions, it seems to be necessary to use a complicated potential as follows,

For satisfying Eq. (4), in a Laplace situation, ∇²Φ=0, the following equations are required, α=β=1, γ=-2. Therefore,

This possibility is generated via four hyperbolic electrodes. In order to achieve such type of electrodes, the surfaces can be considered with the same potential Φ₀/2 and –Φ₀/2, as follow,

These situations make us able to find, and therefore Consequently, electrodes shaped for the potential (4) can be obtained as follows,

Eq. (7) represeznts a hyperbolic equation for this potential. Also, the potential Φ₀ used in hyperbolic electrodes is as follow,

thus, the stochastic potential, (Φ₀)_st , can be written as,

where W_t is a Wiener procedure and η>0 is the noise coefficient determining the size of the stochastic term.14,15 In this regard, the noise coefficient, η, explains the amount of fluctuation potentially. For η = 0, the deterministic potential or normal potential can be stated as (Φ₀)_st = Φ₀. Here, the parameter is selected, therefore is set to be about 14% as a common fluctuation in a potential. Also, the potential Φ_st is usually written as follows,

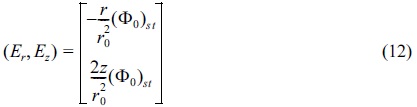
field elements in the trap therefore becomes,

Where ∇ is the gradient. From Eq. (11) we obtain,

The equations of motion for a singly charged positive ion in the QIT is represented thusly,

The a and q are for the z and r parts and the dimensionless parameter ξ are as follows,

where m can be regarded as the ion mass and e as the electronic charge.

Thus, Ω/2π is considered as the drive radio frequency (rf), z₀ as one-half the shortest separation of the end cap electrodes, as the square of ring electrode radius and a_z and q_z as the trapping parameters. The standard Wiener procedure can be defined by a time step dξ as follows,

here, N(0, 1) is seen as the standard normal distribution that is the normal distribution including mean μ = 0 and variance σ² = 1 and density function given as,

In Matlab, the command “randn” was used to add the elements of distribution N(0, 1).

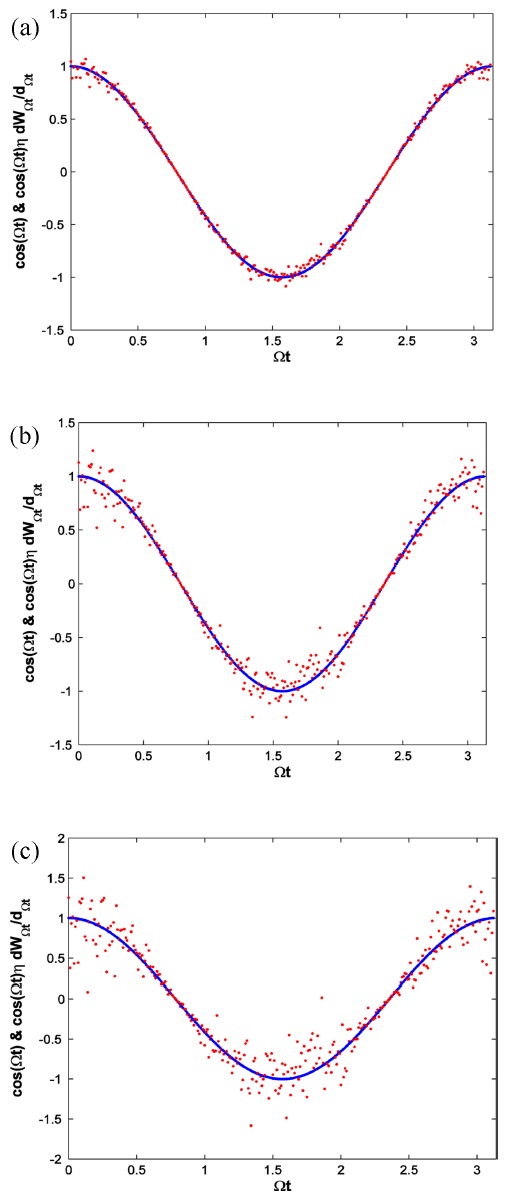
Fig. (3) compares the periodic impulsional potential of the form ηcos(Ωt)/dW_Ωt/d_Ωt, for η=0.0;0.7;0.14;0.28.

Two stability parameters monitor the ion motion for each dimension z (z = z or z = r) and a_z, q_z in the cases of the quadrupole ion trap for deterministic and stochastic cases respectively. The ion's stable and unstable motions, in the plane (a_z, q_z) and for the z axis, can be determined through making comparison between the amplitude of the movement and different values of a_z, q_z. For calculating the precise elements of the motion equations for the stability diagrams, a numerical approach was used. The fifth order Runge-Kutta approach (using 0.001 stepwise increments) was used via the Matlab software as well as the scanning approach.

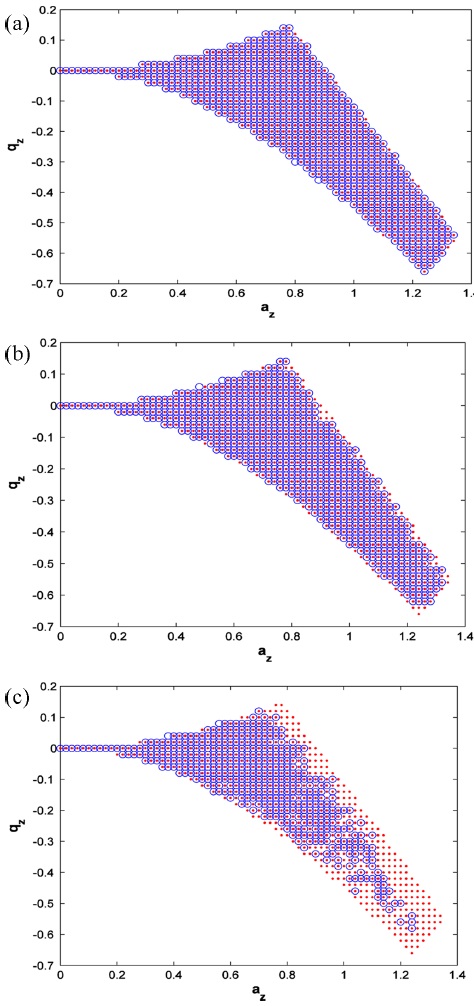
Fig. (4) displays the calculated first stability area for the quadrupole ion traps including and excluding the stochastic potential, red points (red color): QIT, blue circles (blue color): stochastic QIT, (a): η=0.07, (b):η=0.14 and (c): η=0.28. Fig. (4) indicates that increasing noise coefficient η, decreases the first stability area.

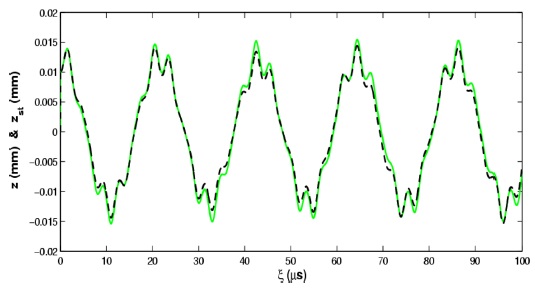
Fig. (5) indicates the ion trajectories in real time for stochastic as well as deterministic cases including a_z=-2a_r=0 and q=-2q_r=0.4 . Indications are done by a solid line (green line): ξ-z for deterministic case, dash line (black line):ξ-z_st for stochastic case when η=0.14. Here “st” stands for “stochastic”.

From a mathematical viewpoint, stochastic as well as theoretical results are closely related. Thus, employing stochastic procedure in quadrupol ion trap potential makes us able to simulate and obtain the numerical outcomes including high accuracy (see Figs. (5)). Table (1) reveals the values of q_z for QIT including and excluding the stochastic potentials for the equivalent points. Thus, two operating points observed in their corresponding stability diagram have the same β_z : β_z=0.3;0.6;0.9. For the computations, the following equations can be used,

Here is the mean of dW_ξ/dξ.

Table (1) indicates the values of q_z for the quadrupole ion trap including and excluding the stochastic potential with η=0.07;0.14;0.28 and β_z=0.3;0.6;0.9 when a_z=0. From Table (1) we see that an increase in the parameter η, will decrease q_z for different values of β.

The values of q_zmax when a_z=0 for the quadrupole ion trap with and without stochastic potential in the first stability region when η=0.07;0.14;0.28 is presented in Table (2).

Table (3) represents the values of V_zmax as a_z=0 for ¹³¹Xe with Ω=2Π×1.05×10⁶ rad/s, U=0 V, z₀=0.783cm in the first stability area when η=0.07;0.14;0.28. Table (3) reveals that as η increases, V_zmax will increase too. To obtain the values of Table (3) by using Eq. (15) we presume V_zmax is the function of m, z₀, Ω², e and is written as follows,

Now, we use Eq. (19) to calculate V_zmax as a_z for ¹³¹Xe with Ω=2Π×1.05×10⁶ rad/s and z₀=0.783cm when η=0;0.14 as follows,

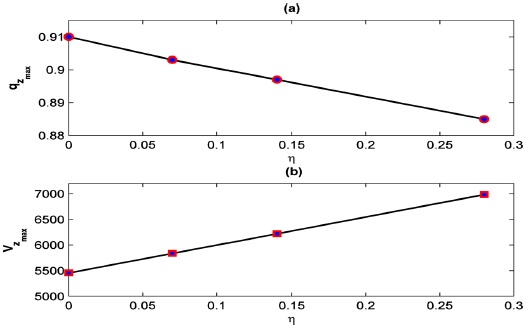
Fig. (6A) shows the behavior of function q_z(η) for β_z=0.3;0.6;09 when a_z=0 . As β_z increase, the difference q_z(0.07)-q_z(0.28) will also increase.

Fig. (6B) shows q_zmax and V_zmax as a function of η in a QIT determined for the first stability area as 0≤η<0.28 in parts (a) and (b), respectively. To plot Fig. (6B), we have to used Table and Table when η=0;0.07;0.14;0.28. Fig. (6B.a) shows that when all factors increase, there is an outcome decrease and Fig. (6B.b) shows that with increasing parameter η; the values of q_zmax increases also. Higher V_rf is shown to have better mass separation particularly for the lower ion mass range.

Generally, the resolution of a quadrupole ion trap mass spectrometry21 can be regarded as a function of the mechanical precision of the hyperboloid of the QIT Δr₀, and the stability performances of electronics tools like, variations in voltage amplitude ΔV and the rf frequency ΔΩ21 which tells us how precise the type of voltage signal used. The present study considers the resolution of a quadrupole ion trap including and excluding stochastic potential. The factor is very significant in plotting stability diagrams and potential for the goal of the mass resolution.

For deriving an influential theoretical formula for fractional resolution, we should consider the stability parameters of the impulse excitation for the QIT including and excluding its stochastic potential, respectively as follows,

By taking the partial derivatives associated with the variables of the stability parameters q_z for Eq. (20) and q_zst for Eq. (21), the expression of the resolution Δm of the QIT including and excluding stochastic potential are as follows,

Now, in order to find the fractional resolution, we have,

here Eq. (24) and Eq. (25) are the fractional resolutions for QIT with and without stochastic potential, respectively.

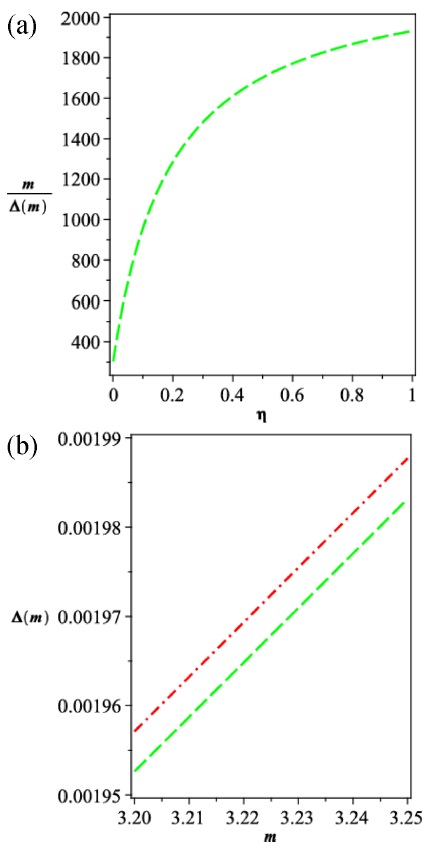
Fig. (7a) indicates the fractional resolution that is a function of the noise coefficient η and Fig. (7b) displays the resolution of Δm that is a function of ion mass m, where a dash dot line (red line); represents deterministic cases (η=0) and dash lines (green line) represent stochastic case (η=0.14).

Regarding the fractional mass resolution, the following uncertainties were used for the voltage, rf frequency and the geometry; ΔV/V=10^-5, ΔΩ/Ω=10^-7, Δr₀/r₀=3×10^-4, for η=0;0.07;0.14;0.28 we have assumed arbitrarily the the noise coefficient Δη = 10^-2. The fractional resolutions obtained are (m/Δm)_st=298;812;1113;1448 for η=0;0.07;0.14;0.28, respectively. When stochastic potential is applied (η=0.14), the limited voltage of rf increases by a factor of approximately 1.14; thus, the voltage uncertainties were taken as ΔV_st/V_st=1.14×10^-5. Once these fractional resolutions were considered for the tritium isotope mass m=3.202348, then, Δm=0.001954 and 0.001959 with and without stochastic potential, the values for η=0 and η=0.14 were achieved, respectively.

Theoretically, we have,

Thus, (m/Δm)_st≥m/Δm. This means that, along with increasing η the value of m/Δm will increase. Therefore, the power of resolution will increase because of the reduction in Δm. Experimentally, this means that the width of the mass signal spectra is better separated.

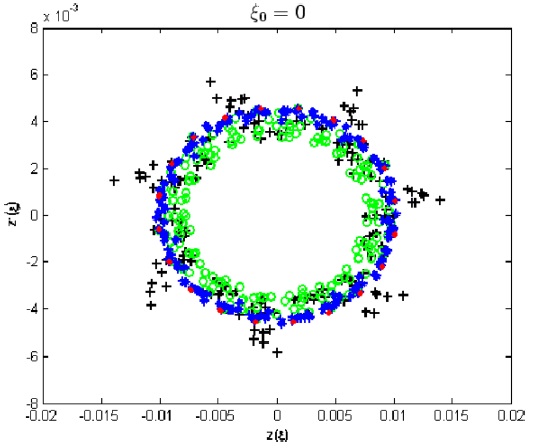
Fig. (8) indicates the evolution of the phase space ion trajectory for different values of the phase ξ₀=0 for β_z=0.3 where by a red line indicates η=0 (q_z=0.40944), a blue line a blue line indicates η=0.07 (q_z=0.40659), a green line indicates η=0.14 (q_z=0.40379) and a black line for η=0.28 (q_z=0.39829).

The results represented in Fig. (8) indicates that for the same equivalent operating point in the two stability diagrams (having the same β_z=0.3), the associated modulated secular ion frequencies behavior is almost the same for different values of η=0;0.07;0.14;0.28.

From a mathematical point of view, the results of stochastic process has higher resolution during mass separation. It has been shown that (m/Δm)_st≥m/Δm, this means that, with increase in η the value of m/Δm also increases and therefore the power of resolution increases too due to a reduction in Δm. Empirically, the width of the mass signal spectra seems to be better separated. Anyway, at least in the lower mass range, the impulse voltage including the stochastic potential is clearly quite suitable for the quadrupole ion trap with higher mass resolution. The fractional resolutions obtained are (m/Δm)_η=0=298 and (m/Δm)_η=0.14=1113; therefore, (Δm)_η=0.14<(Δm)_η=0 and this indicates that η=0.14 when higher resolution in mass separation is involved.

All authors read and approved the final manuscript.

The authors declare that they have no competing interests.