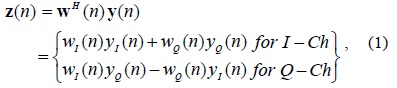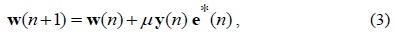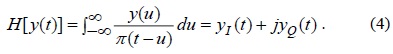Because of the reflections from the boundaries in underwater acoustic communication, the communication channel used is known to exhibit a frequency-selective fading channel with a multipath delay spread [1-3]. The performance of the underwater acoustic communication system degrades because of the inter-symbol interference (ISI) [4,5] caused by the signals reflected from the sea surface and the sea bottom. A channel estimation-based equalizer is usually adopted to compensate for the ISI effect [5,6].
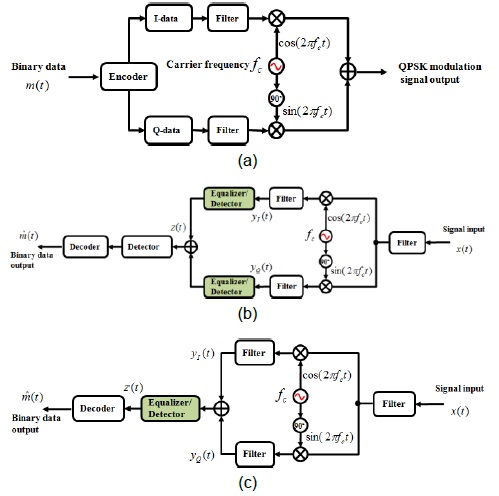
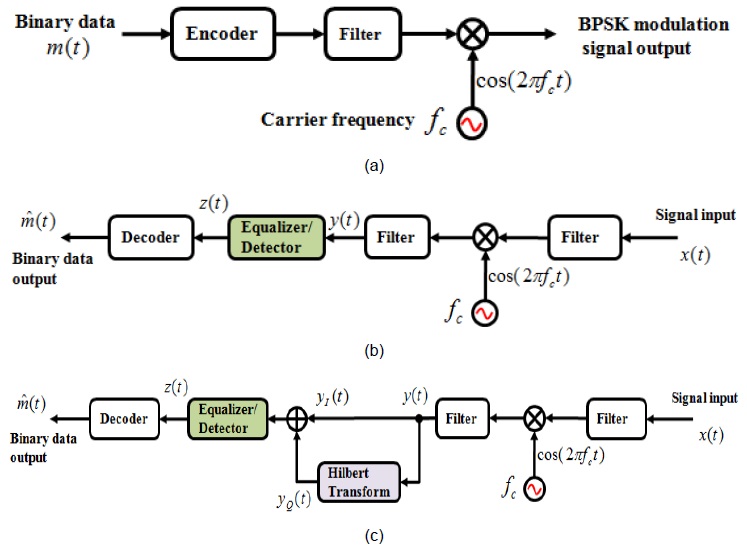
In this study, a feed-forward equalizer (FFE) with the least mean squares (LMS) algorithm is applied to the quadrature phase-shift keying (QPSK) transmission system in order to cancel out the ISI effect [7,8]. Two types of equalizers are introduced, namely a real-coefficient equalizer and a complex-coefficient equalizer. We also introduced a binary phase-shift keying (BPSK) system with two real- and a complex-coefficient equalizers. For the imaginary part such as the quadrature (Q) channel of the QPSK system, a Hilbert transform was used in the BPSK system [9,10].
The rest of this paper is organized as follows: in Section II, a comparison of two types of equalizers is presented. In Section III, simulation configurations are introduced. Section IV presents the concept of the complex-coefficient BPSK system. In Section V, the simulation results and the experimental results of the proposed methods are discussed. A summary of the performance of the proposed method is presented in Section VI.
II. COMPARISON OF TWO TYPES OF EQUALIZERS
In general, there are two binary state channels, namely the in-phase (
When an equalizer for the compensation of the channel distortion is applied to the output signals, two types of systems are considered. The first type of system includes two separated real-coefficient equalizers for each output
III. SIMULATION CONFIGURATIONS
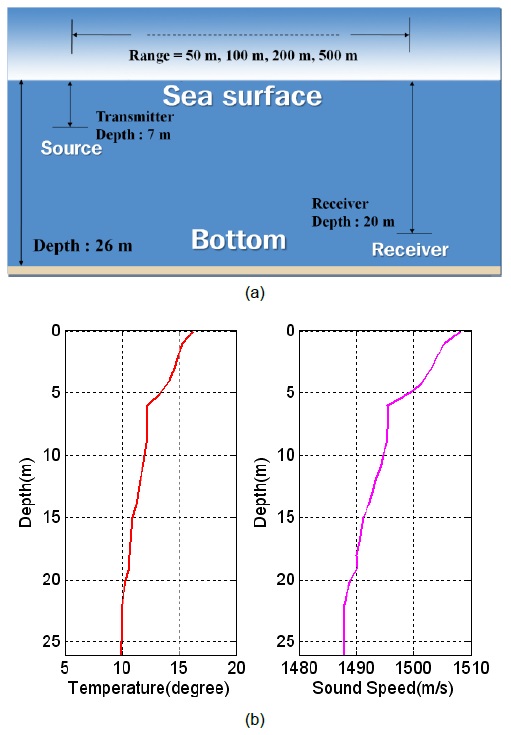
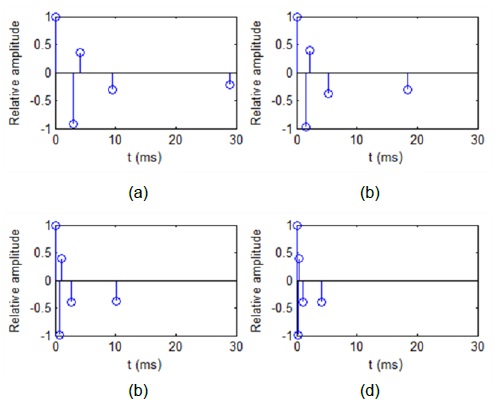
Fig. 2 shows a layout of the experimental geometry at the bay of the Gwangan Beach located on the east side of Busan city, Korea. The range between the transmitter and the receiver is set to be 50, 100, 200, and 500 m. The depths of the transmitter and the receiver are set to be 7 m and 20 m, respectively. As the temperature and the sound speed of the vertical depth were almost flat, an image method [11] was used for the implementation of the underwater acoustic communication channel, and the related channel impulse responses are shown in Fig. 3.
We assumed that the channel response had five impulse signals: direct signal, surface-reflected signal, bottom-reflected signal, surface-bottom-reflected signal, and bottom-surface-reflected signal. The sampling frequency and the carrier frequency are set to be 160 kHz and 20 kHz, respectively. The transmission rates are set to be 500, 1000, 2000, and 4000 symbols per second (sps). The transmitted image is a standard Lena image that consists of 50 × 50 pixels with an 8-bit resolution (20,000 bits).
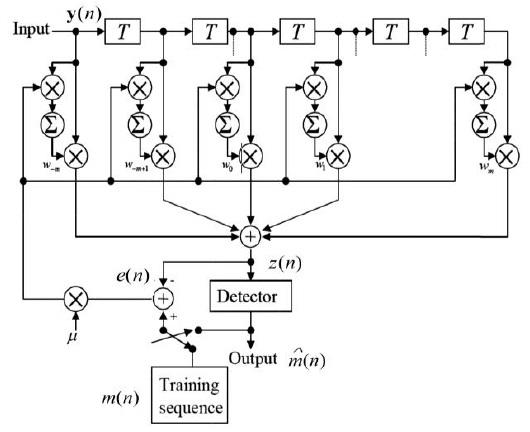
Fig. 4 shows the block diagram of the FFE with the LMS algorithm. Here, m(
where
IV. CONCEPT OF COMPLEX BPSK SYSTEM
In this section, we introduce a complex BPSK system based on the concept of the QPSK system. The BPSK system has the same structure as the
It was obtained using the imaginary signal
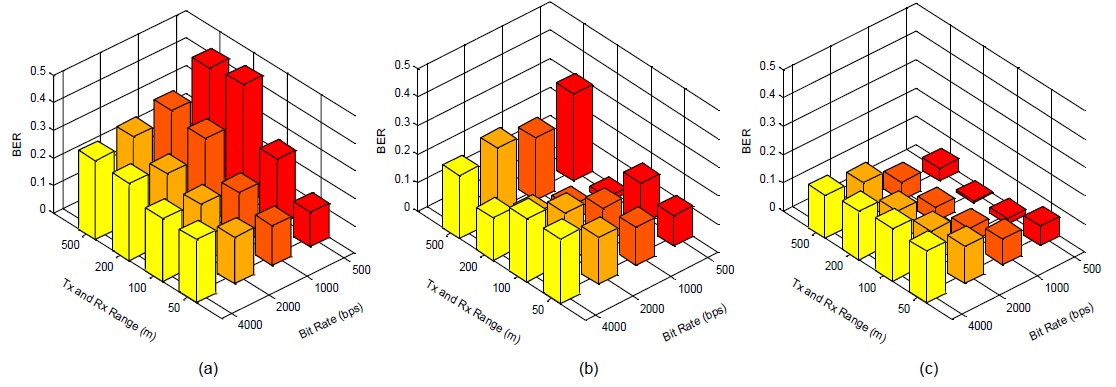
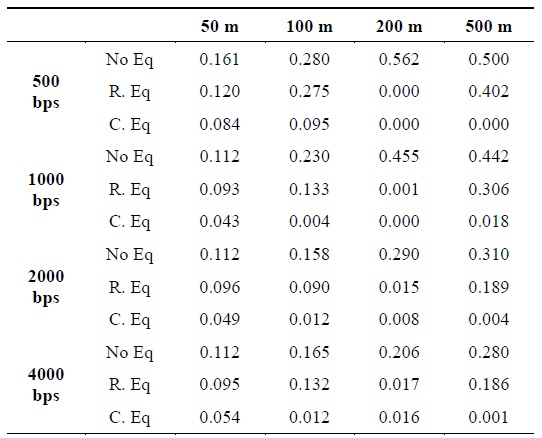
First, the simulation results of two different equalizers of the QPSK system are presented. The bit error rates (BERs) according to the transmission rate and the range are presented in Fig. 6 and Table 1, respectively.

Comparison of results obtained using the QPSK system with two different types of equalizers
In Fig. 6, (a) shows the result obtained without the use of an equalizer; (b) the result obtained using two real-coefficient equalizers; and (c) the result obtained using a complex-coefficient equalizer. The same number of iterations for the training of the coefficient on the FFE is set for each simulation. From the obtained results, we concluded that the complex-coefficient LMS equalizer shows a better performance than the two separated real-coefficient LMS equalizers. The filter’s output signal z(
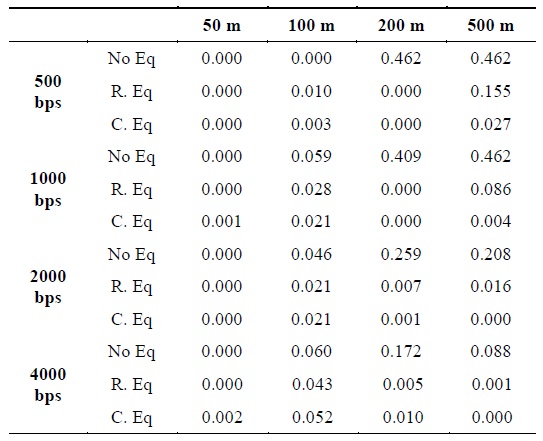
Second, Fig. 7 and Table 2 show the simulation results of two different equalizers in the BPSK system. In Fig. 7, (a) shows the result obtaining without using the equalizer; (b) the result obtained using a real-coefficient equalizer; and (c) the result obtained using a complex-coefficient equalizer. The same number of iterations for the training of the coefficient on the FFE is set for all the simulations. Further, the results obtained using the complex-coefficient LMS equalizer were better than those obtained using the real-coefficient LMS equalizer in the BPSK system.
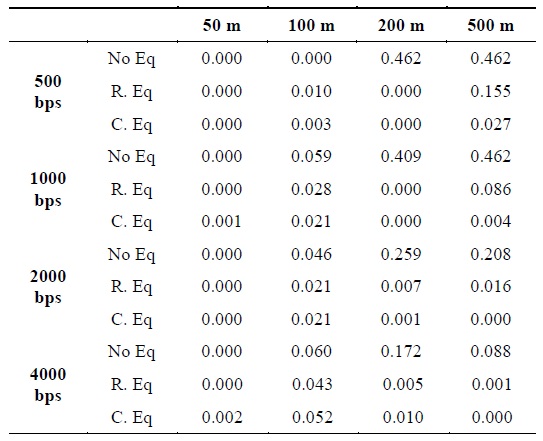
Comparison of results obtained using the BPSK system with two different types of equalizers
Finally, Fig. 8 shows the results of the equalization of the experimental data, carried out in a shallow ocean. The experimental conditions are the same those as shown in Fig. 1. The distance between the transmitter and the receiver was 10 m, and the bit rate was chosen to be 50 sps. In Fig. 8, (a) shows an original Lena image, (b) presents the result obtained without using an equalizer (BER=0.224), (c) and (d) illustrate the results with two real-coefficient equalizers (BER=0.181) and a complex-coefficient equalizer (BER= 0.123), respectively. Therefore, we can conclude that the complex-coefficient equalizer performs better than the two real-coefficient equalizers.
In this study, an FFE with the LMS algorithm was applied to the QPSK system, and two real-coefficient equalizers and a complex-coefficient equalizer were adopted; their results were compared. The performance of a complex-coefficient equalizer was better than that of the two real-coefficient equalizers. On the basis of the results of the QPSK system, a Hilbert transform was applied to the real-coefficient BPSK system in order to obtain the complex-coefficient BPSK system. Further, the performance of a complex-coefficient equalizer was better than that of the two real-coefficient equalizers in the BPSK system.