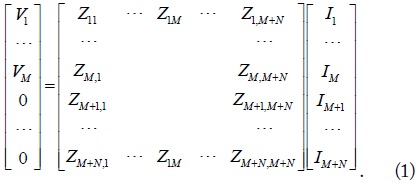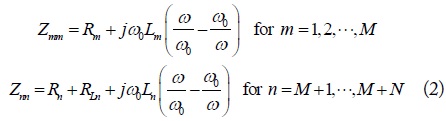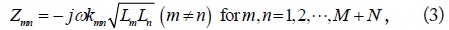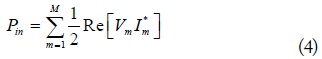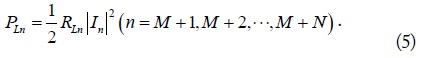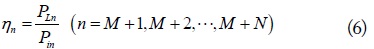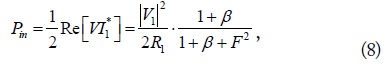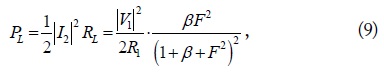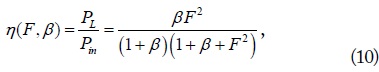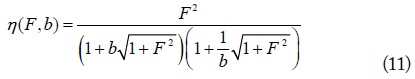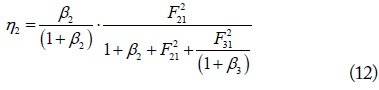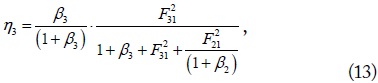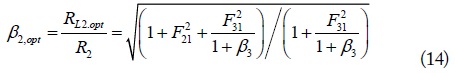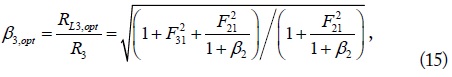Wireless power transfer (WPT) efficiencies for multiple-input multiple-output (MIMO) systems are formulated with a goal of achieving their maximums using Z matrices. The maximum efficiencies for any arbitrarily given configurations are obtained using optimum loads, which can be determined numerically through adequate optimization procedures in general. For some simpler special cases (single-input single-output, single-input multiple-output, and multiple-input single-output) of the MIMO systems, the efficiencies and optimum loads to maximize them can be obtained using closed-form expressions. These closed-form solutions give us more physical insight into the given WPT problem. These efficiencies are evaluated theoretically based on the presented formulation and also verified with comparisons with circuit- and EM-simulation results. They are shown to lead to a good agreement. This work may be useful for construction of the wireless Internet of Things, especially employed with energy autonomy.
Recently, the wireless power transfer (WPT) technology has become more important, and products related to single-input single-output (SISO) WPT systems have been globally commercialized with the example of wireless charging pads [1]. To expand the WPT market, regulatory issues regarding WPT commercialization and standardization are being finalized [2]. The WPT systems with multiple transmitters or multiple receivers have also been studied [3–5]. In [3], multiple-input single-output (MISO) WPT systems were investigated using closed-form solutions for the maximum WPT efficiencies. An analysis of the WPT efficiencies considering the multiple-output system was provided in [4]. Multiple-input multiple-output (MIMO) WPT systems including a repeater with a misalignment angle were examined in [5].
Still, there are many problems left in WPT systems, such as low efficiency, realization, stability, adaptability to mobility, EMI/EMC/EMF, and so on. In this paper, the WPT problem for general MIMO systems is formulated to achieve maximum efficiencies based on optimum loads. The maximum efficiencies of the systems can be obtained systematically for any number of transmitters and receivers. With this formulation, the optimum loads for maximum efficiencies can always be found at least numerically through a proper systematic optimization process. For some special cases such as SISO, SIMO, and MISO, closed-form expressions for the efficiencies and optimum loads for maximum efficiencies are derived and examined with various examples. The validity of circuit- and EM-simulated efficiencies are compared with the theoretical efficiencies.
II. MIMO WIRELESS POWER TRANSFER SYSTEM
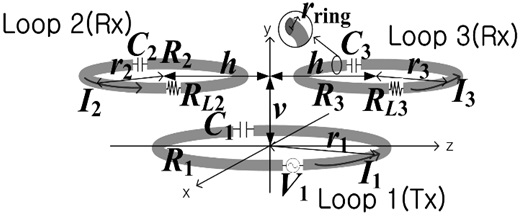
Fig. 1 shows a WPT system consisting of transmitters with a number of
In (1), the elements in the column matrix [
and
respectively. In (2),
At the resonant angular frequency (
and
The WPT efficiencies for the
and
respectively. Based on this formulation, the WPT efficiencies for any MIMO configurations with arbitrary loads
When the number of transmitting and receiving loops is 1 (
and
respectively, where the normalized load
where
III. ANALYSIS OF WIRELESS POWER TRANSFER FOR SPECIAL CASES
1. Single-input Multiple-Output System (M = 1, N = 2)
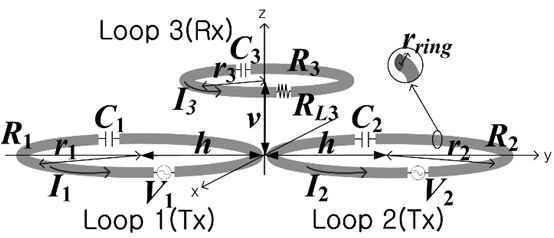
Fig. 2 shows a WPT system consisting of one transmitter and two receivers. The center positions of each loop are assumed to be at (0, 0, 0), (0, -
When the distance between the two receiving loops is large, the coupling coefficient
and
where
and
respectively. When
All the efficiencies and optimum loads evaluated and presented in this paper have been checked between the GA results based on (2)–(7) and circuit/EM-simulation results. The efficiencies and optimum loads have been found to be always in good agreement.
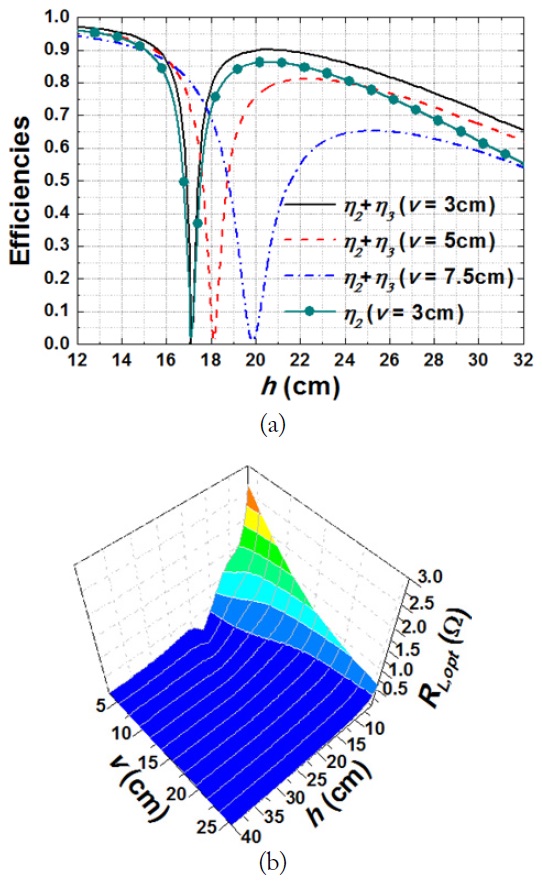
Fig. 3(a) and (b) show the maximum WPT efficiencies and the optimum load resistances for the case described in Fig. 2. The resonant frequency is 6.78 MHz,
In Fig. 3(a), the efficiency
This means that when the Rx loops are properly placed in symmetry relative to the Tx loop, the nearly 100% efficiency can be shared by the receiving loops. When
Beyond the zero-efficiency (or the zero-coupling coefficient) positions, the net magnetic flux lines on the receiving loops go downward (the negative
In Fig. 3(b), we show
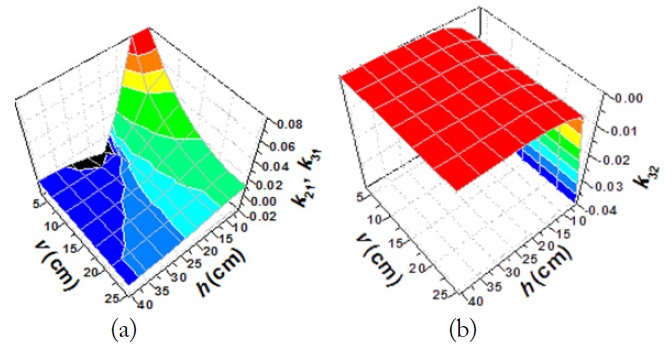
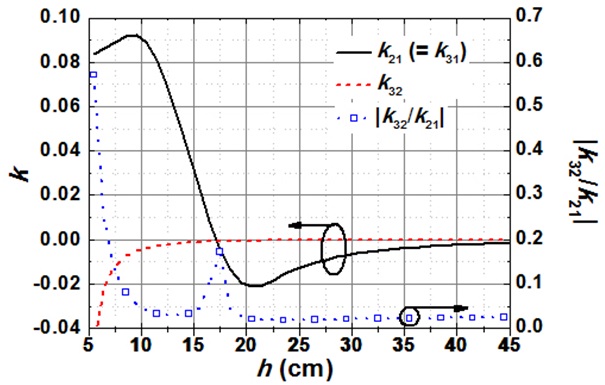
Fig. 4 shows the coupling coefficients
Fig. 5 shows the coupling coefficients
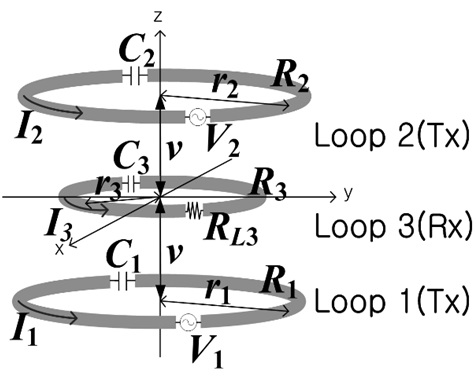
2. Multiple-Input Single-Output System (M = 2, N = 1)
Fig. 6 shows a MISO configuration consisting two transmitters and one receiver. The center positions of each loop are (0,
Fig. 7 shows the maximum WPT efficiencies for the system-described in Fig. 6. The resonant frequency is 6.78 MHz,
In Fig. 7, the maximum efficiency
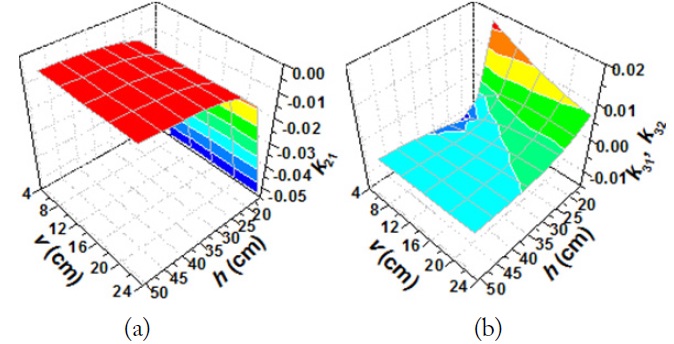
Fig. 8 shows the coupling coefficients
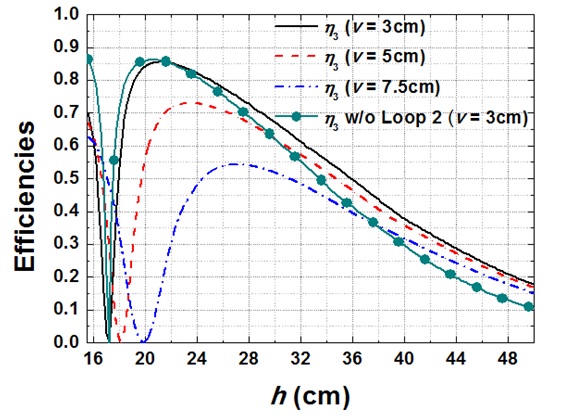
Fig. 9 shows a MISO system (
Fig. 10(a) and (b) show the WPT efficiency
When
3. Multiple-Input Multiple-Output System (M = 2, N = 2)
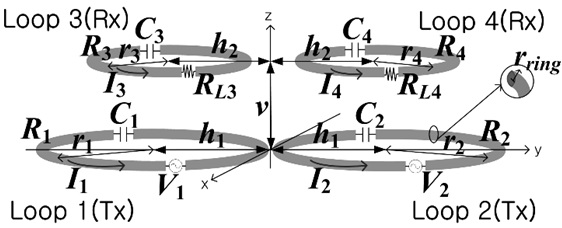
Fig. 11 shows a MIMO system (
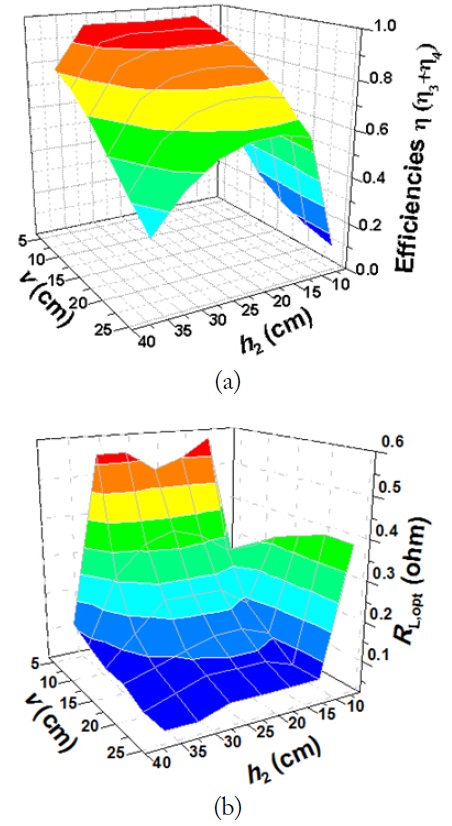
Fig. 12(a) and (b) show the WPT efficiencies and the optimum load resistances for the case described in Fig. 10. The resonant frequency is 6.78 MHz,
In Fig. 12(a),
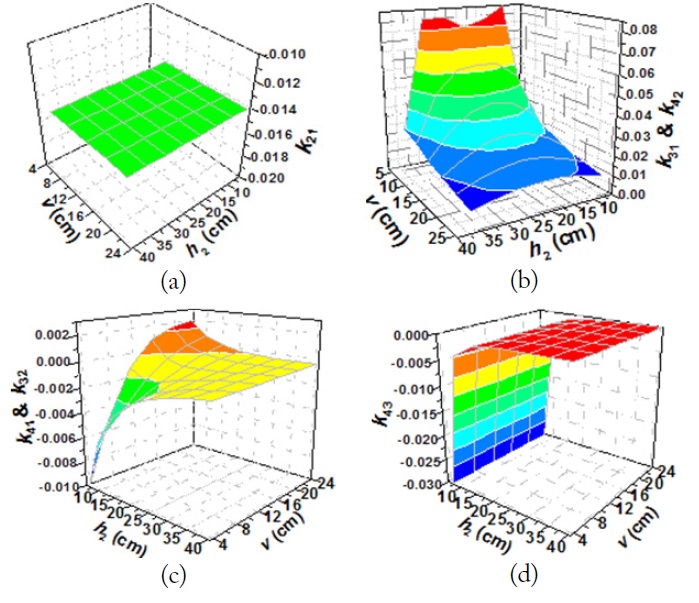
Fig. 13 shows the coupling coefficients
Since the MIMO WPT systems are considered to be a natural extension of the SISO system, the overall WPT system efficiencies have been found to be well above 90% when the distances between the TX and Rx loops are roughly less than the radius of the Tx loops.
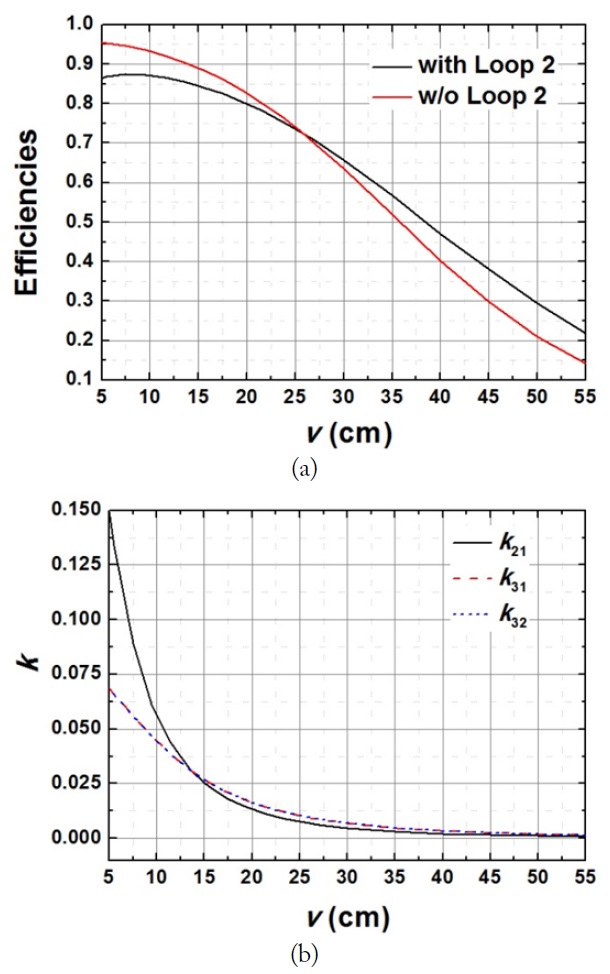
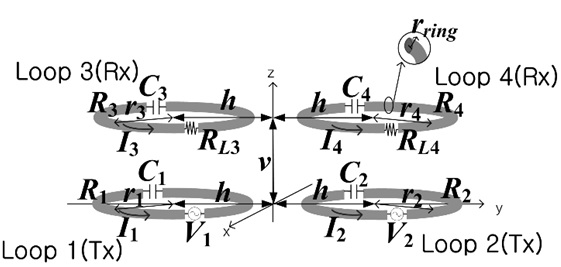
Fig. 14 shows a MIMO system (
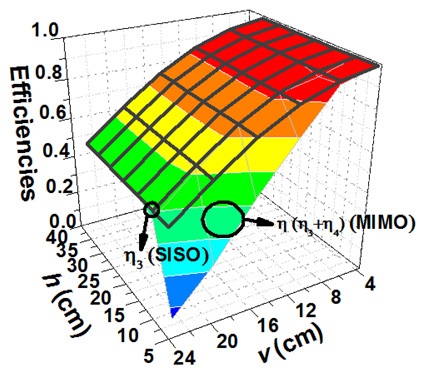
Fig. 15 shows the WPT efficiencies for the case described with all loops (MIMO) or without loop 2 and loop 4 (SISO) in Fig. 14. The resonant frequency is 6.78 MHz,
In Fig. 15,
Although the EM simulation results have been analyzed and discussed up to
In particular, for the WPT system with
We formulated the MIMO WPT systems in terms of transfer efficiencies for each receiver and the whole receivers. The optimum loads of the receivers for the maximum WPT efficiencies have been shown to be found at least numerically based on the formulation. For some typical special cases of SISO, MISO, and SIMO system have been analyzed using circuit- and EM-simulations together with the derived closed-form solutions. In particular, the SIMO system has been shown to be effective in that the near 100% efficiency can be shared by the receiving loops. The derived closed-form solutions have been demonstrated to give us plentiful physical insight for the systems. The results of this paper may be useful to construct WPT systems for Internet of Things requiring sensors with energy autonomy without batteries.