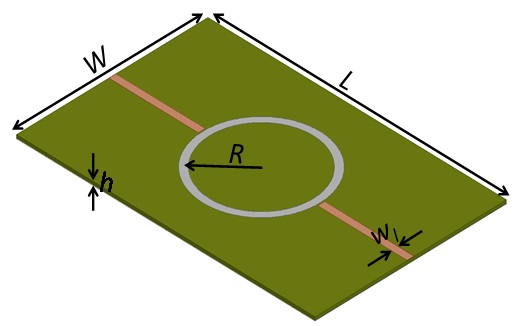
In recent years, wearable antennas for body-worn communication systems have been studied extensively [1]. One way to realize such antennas is by using conductive fabrics [2]. Such fabrics are highly flexible, durable, and restorable, and they can be directly integrated onto clothing by ordinary sewing or embroidering techniques. To derive an appropriate antenna design, it is essential to have accurate information about the electrical properties of conductive fabrics, especially the conductivity (
Commonly, the manufacturers of conductive fabrics provide the DC sheet resistances (
Many studies have measured the RF permittivity of dielectrics. However, few studies have measured the conductivity of highly conductive materials at RF. In [6,7], a planar resonator is used as a test fixture to measure the quality factor (Q-factor) with the conductor under test inserted in. Then, the conductor’s
As an alternative, full-wave simulation data can be used to estimate the conductivity instead of the approximate closed-form equations.In a full-wave simulation tool, a structure identical to the material under test is modeled, and then, the simulation data is collected by varying the material properties (e.g.,
In this paper, we present a conductivity measurement method by employing a planar ring resonator (shown in Fig. 1) and surrogate-based optimization (SBO) [10] as the root-searching tool. Section II provides an outline of the measurement process. Section III demonstrates the effectiveness of the proposed method by measuring a copper ring with known conductivity. Section IV discusses the conductivity measurement of the Zell fabric. The results appear to be within the order of 104 S/m, which is lower than the DC conductivity of the order of 105 S/m reported by the manufacturer.
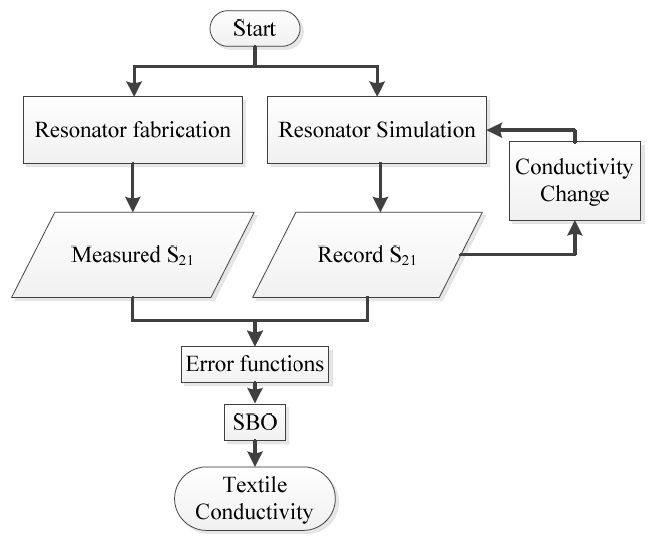
II. OVERVIEW OF PROPOSED MEASUREMENT METHOD
Fig. 2 shows a flowchart of the conductivity measurement process. A microstrip ring resonator with
Meanwhile, a resonator identical to the fabricated one is modeled in a full-wave simulation tool (Ansys HFSS). The conductivity of the ring in the simulation model is varied to collect a set of
III. MEASUREMENT WITH COPPER RING RESONATOR
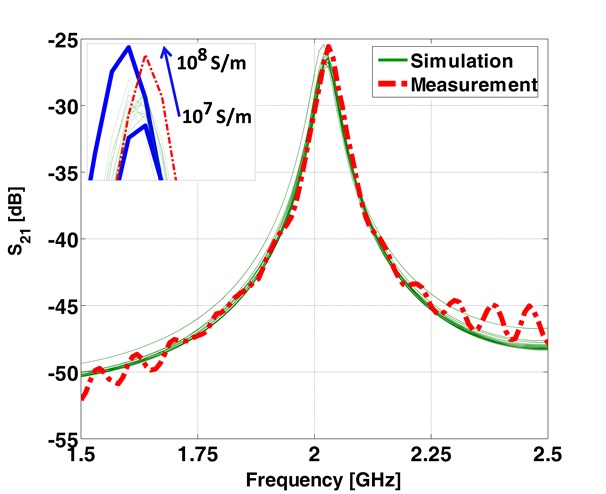
The proposed measurement method is first tested with a ring made of copper. Fig. 3 shows the fabricated copper ring resonator and Fig. 4, the measured and simulated
The set of simulated
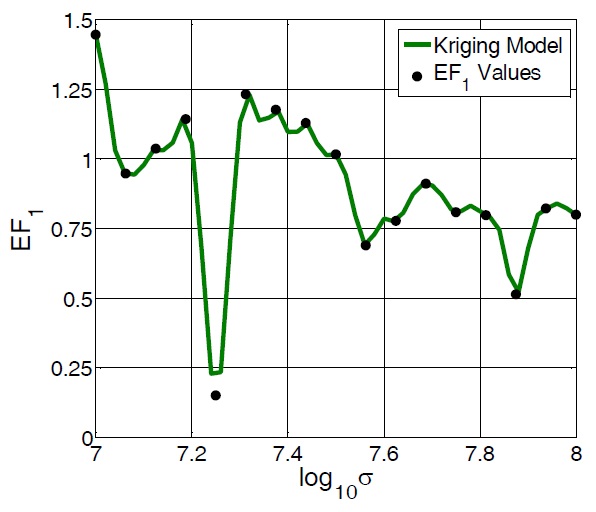
where are the magnitudes of the simulation and measurement at the resonant frequency. Fig. 5 shows the error function values along the sampled conductivity points and the interpolated Kriging model after the SBO process. The error function is minimum at
IV. MEASUREMENT OF ZELL FABRIC
After measuring the conductivity of copper using the proposed method, we measured the conductivity of the Zell fabric, a metalized nylon fabric. The Zell fabric under test has a thickness of 0.1 mm and DC surface resistance as low as 0.02 Ω/sq [5], corresponding to a DC conductivity of 5×105 S/m.
Fig. 6 shows the microstrip ring resonator with the ring made of Zell fabric. The Zell fabric ring is attached on the FR-4 substrate using fast-drying urethane glue. The glue has trivial influence on the resonator performance because its layer is very thin and its relative permittivity (3.2 at 23℃) is close to that of the FR-4 used. On the other hand, a ring resonator with the same dimension as that shown in Fig. 6 was modeled in the full-wave EM simulator, and
As shown in Fig. 7, the simulated
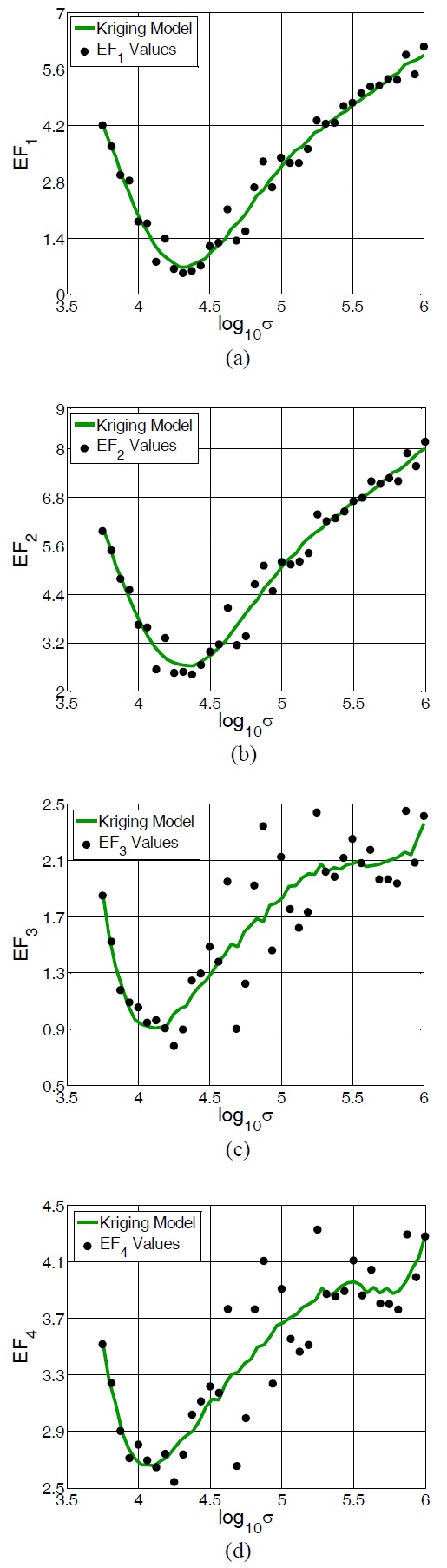
For the conductivity retrieval process, we test four different error functions in addition to
where are the phase of the simulated and measured
The SBO toolbox compares the simulated and measured data using the abovementioned error functions to determine the conductivity of the Zell fabric. Fig. 8(a)–(d) show the resulting Kriging models when
The error function minima for
In this paper, a new measurement technique for evaluating RF conductivity is described. The proposed method employs a microstrip ring resonator, full-wave simulation data, and SBO optimization technique to measure the conductivity of a conductive fabric at a microwave frequency. We first evaluated the conductivity of plated copper using the proposed method, and then, we applied it to measure the conductivity of a Zell fabric. For both cases, the conductivity values around 2 GHz were lower than the known DC conductivity. This is because high-frequency currents mostly flow along the surface owing to the skin effect and concurrent influence of the surface roughness of the conductor. Therefore, it is important to measure the high-frequency conductivity of newly introduced conductive materials to formulate an accurate model of antennas and RF components.