A De-Embedding Technique of a Three-Port Network with Two Ports Coupled

Pu
						Bo; Kim
						Jonghyeon; Nah
						Wansoo

doi:10.5515/JKIEES.2015.15.4.258

OA학술지
Journal of electromagnetic engineering and science

A De-Embedding Technique of a Three-Port Network with Two Ports Coupled

DOI : 10.5515/JKIEES.2015.15.4.258
Author: Pu Bo, Kim Jonghyeon, Nah Wansoo
Publish: Journal of electromagnetic engineering and science Volume 15, Issue4, p258~265, 31 Oct 2015

ABSTRACT

A de-embedding method for multiport networks, especially for coupled odd interconnection lines, is presented in this paper. This method does not require a conversion from S-parameters to T-parameters, which is widely used in the de-embedding technique of multiport networks based on cascaded simple two-port relations, whereas here, we apply an operation to the S-matrix to generate all the uncoupled and coupled coefficients. The derivation of the method is based on the relations of incident and reflected waves between the input of the entire network and the input of the intrinsic device under test (DUT). The characteristics of the intrinsic DUT are eventually achieved and expressed as a function of the S-parameters of the whole network, which are easily obtained. The derived coefficients constitute ABCD-parameters for a convenient implementation of the method into cascaded multiport networks. A validation was performed based on a spice-like circuit simulator, and this verified the proposed method for both uncoupled and coupled cases.

KEYWORD

Coupled Lines , De-Embedding Method , Multiport Network , Odd Number Ports

본문

Collapse all

I. INTRODUCTION

As a frequency continues to increase, the scattering parameter (S-parameter) seems to be a crucial factor to estimate the performance of high speed and microwave components. One of the reasons is that the impedance matching is easily achieved to obtain the S-parameter in real applications. At the same time, the Z-parameter and Y-parameter are significantly more difficult to measure at high frequencies, as open- and short-circuit conditions are not easily met [1-3].

Both in analog and digital applications, many passive structures of interest are embedded between microstrip or strip lines. If one desires to characterize such structures by S-parameter measurements, it is quite difficult to separate the actual part in which we are interested from its environment [4]. Normally, the device under test (DUT), which is widely seen as a part embedded in the test setup, is connected with certain types of test fixtures, whereas it is not connected directly to the calibrated reference plane of the vector network analyzer (VNA). The effects of test fixtures distort the measurement results and they must be de-embedded for the highest quality measurement [5-7].

In this paper, we propose a de-embedding method for multiport networks, especially for coupled odd interconnection lines, based on the scattering matrix (S-matrix). This paper is organized as follows. Section II describes the existing and our proposed de-embedding techniques for uncoupled multiport networks. Section III demonstrates our proposed de-embedding method for the coupled multiport networks in detail through the conversion of the S-matrix. Then, general cases to implement the proposed methods for both uncoupled and coupled interconnection lines are discussed in Sections IV and V. Finally, Section VI presents our conclusion.

II. MULTIPORT DE-EMBEDDING TECHNIQUES FOR UNCOUPLED INTERCONNECTION LINES

The S-matrix is an approach to express the S-parameter in a matrix form. The S-parameters relate amplitudes (magnitude and phase) of traveling waves that forward on and that are reflected from a microwave network, and the reference plane of a phase must be specified for each port to the network [5]. The de-embedding method is meant to extract the characteristics of the intermediate connection part between the measured port and the port of the actual part in which we are interested.

   1. Lossless and Uncoupled Lines with Matched Load

When the load is matched to the generator, Z_g = Z_L, and they are interconnected through the matched transmission line with length l_i, we have a matched condition, and there is only a phase shift for the change of the reference plane in a lossless transmission line. The θ_n = β_nl_n, is the electrical length measured outward shift of the reference plane of port n.

Based on the equation obtained above, we can conclude that S’_NN = e^{−2j^θN}, as expressed in (1) and (2). In addition, the S’_NN represented the phase of the origin S_NN in the input of the intrinsic DUT, which is shifted by twice the electrical length of the shift in the terminal plane n, as there are round paths of incidence and reflection, and the wave travels twice over the length [1].

   2. Unmatched Load Condition Solved by Generalized S-Parameters

Practically, the characteristic impedances of a multiport network may be different, where the solution for the matched case is no longer applicable. Herein, a generalization of the S-parameters is required to handle the effects of the unmatched load.

The relationship between the incident and reflected waves for an arbitrary load condition can be expressed by a generalized S-matrix, as in (3). The S-matrix is composed of the self and coupled S-parameters of the N-port network, and the definition of the S-parameter in a network with an identical characteristic impedance is indicated in (4).

As the characteristic impedance of the interconnection lines does not equal the load, a new set of wave amplitudes is demanded, as in (5) and (6).

In the unmatched load case, a modification has been added to (4) to obtain (7), which is the S-parameter for each item to generalize the matrix [1].

   3. De-Embedding Techniques for Uncoupled Interconnection Lines

An N-port network is shown in Fig. 1, where Z₀_n is the characteristic impedance of the nth interconnection, and the primed letters a' and b' illustrate the incident and reflected waves at the available port for measurement, respectively. The unprimed letters, a and b, are the incident and reflected waves for the output port of the interconnection lines, while they are also the reflected and incident waves for the input port of the DUT.

[Fig. 1.] A schematic for uncoupled N-port interconnections.

The transfer S-parameters mentioned are unable to be applied to solve the de-embedding issue that occurred in oddnumber independent ports, as illustrated in Fig. 1, because the conversion is based on the relations of the basic two-port network. Herein, we propose a method based on the definition of S-parameter, which relates incident and reflected waves, as expressed in (8).

In the equation above, the unprimed a_i and b_i and their defined [S] are the required characteristics of the DUT that cannot be measured directly. However, the unprimed element a_i is represented as (9) by the available primed elements from the first row of (8).

In the same way, the element b_i of (8) can be expressed by the primed incident and reflected waves as in (10) via substituting (9) into the second row of (8).

As a combination of (9) and (10), the incident and reflected waves only for the DUT are obtained as expressed in (11),

where the coefficients M_i, N_i, P_i, and Q_i in the matrix above have a detailed description in (12).

The derivations of the mentioned equations are based on a two-port network system, and calculated equations can also be represented as a matrix form, as expressed in (13), to extract the intrinsic S-parameter of the DUT from the whole system with the characteristics of interconnects.

In this uncoupled interconnection lines case, matrices [M], [N], [P], and [Q] are the only diagonal matrices to avoid the coupling effects between each line, and the diagonal entries of the matrices come from the mentioned coefficients M_i, N_i, P_i, and Q_i, respectively.

As the incident and reflected waves are difficult to measure directly, a modification has been made to (13). The S-parameter, which is the ratio of incident to reflected waves, could be a substitution of those waves, as expressed in (14), because the S-parameter can be obtained by the VNA. In the equation, the matrix [S’] represents the directly measured result of the whole network, and matrices [M], [N], [P], and [Q] are the characteristics of the interconnection lines.

The coefficients in (14) can be both even-order and oddorder matrices, so the proposed method is appropriate for the de-embedding techniques of odd-number uncoupled ports.

The method developed in [8] is another approach for providing a solution in an odd-number case. In that reference, a general three-port de-embedding method using shield-based test structures for a microwave on-wafer characterization is presented. The surrounding parasitic of a DUT has been shielded to realize the uncoupled de-embedding techniques.

III. MULTIPORT DE-EMBEDDING TECHNIQUES FOR COUPLED INTERCONNECTION LINES

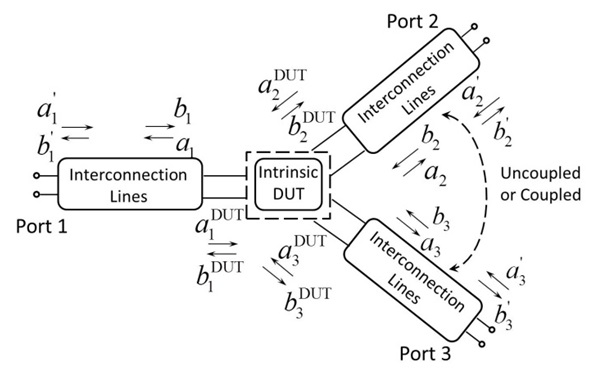
In the real modern electronic system, the interconnectors in the input and output terminals are usually multi-port, and there are inevitable coupling effects generated among the closed interconnection lines. As the coupled phenomenon for a multiport is so complicated that it requires a separate analysis for a detailed explanation, in this step, we only consider the most common case for a three-port network with two ports coupled, as illustrated in Fig. 2. In the three-port network with two ports coupled, the non-diagonal entries in the coefficient matrices M, N, P, and Q of (14) are no longer null, but this depends on the coupling magnitude. The method mentioned in [5] was unable to accurately convert the T-matric back to the S-matrix, as there are fewer elements in the calculated T-matrix (8 elements for the 2 by 4 [T_DUT]) than in the S-matrix (9 elements for the 3 by 3 [S_DUT]) with the unbalanced condition as illustrated in Fig. 3. Therefore, it cannot obtain the required S-parameter of the DUT, even when we have successfully derived the T-parameter of the DUT. The method in [8] cannot handle de-embedding with coupled interconnection lines, as it is a shield-based threeport network. Herein, we proposed a method for de-embedding the coupled two ports accurately to avoid the disadvantages of the two methods mentioned above.

[Fig. 2.] A schematic to describe the uncoupled or coupled three-port network.

[Fig. 3.] An unbalanced three-port network consisting of a cascaded T-parameter.

The proposed method has a derivation similar to the approach method in Section II, and the difference in the nondiagonal entries of the coefficient matrices in the conversion of S-parameters here is not null and represents the coupling effects.

Herein, the derivation started with a three-port model, where port 2 and port 3 are coupled with each other. The characteristic of interconnection for port 1 is described as (15), which is the same as the uncoupled situation. Changes happened in (16), where the non-diagonal entries indicate the coupling effect but are not null, as in the uncoupled case.

Each incident and reflected wave of the DUT is easily obtained by the equations constituted by the four rows of (16), and the relationship represented by the [C] matrix between the external ports and terminals of the DUT are reformed, as expressed in (17). Especially, the unprimed a_i and b_i in the output port of the interconnection lines are simply the in the input port of the DUT.

A matrix expression of the S-parameters of the three-port network based on both the transmission and the reflected waves is described in (17). Then, a re-arrangement of (17) can achieve a matrix expression with the waves at the ports of the DUT on one side and the other waves at the measured ports on another side, as shown in (18). Thus, the [C] matrix is easily obtained by an operation of the matrix transformation based on the different relationships of incident and reflected waves.

where the [C] matrix is described as:

Each term of the new [C] matrix is a composition of the S-matrix, and the 6 by 6 [C] matrix is divided into four 3-by-3 sub-matrices, as demonstrated in (19). The terms of the [C] matrix are calculated based on the matrix operation, as expressed in (20)–(25). The equation of the S-parameter in each term of the [C] matrix is also obtained based on the conversion of the [S] matrix in (18).

Thus, a new expression of (16) is achieved in (26) for deriving the final S-parameter of the DUT. The required S-parameter of the DUT is represented in (27) by the [C] matrix and the S-parameter of the whole network, which can both be obtained through a derivation and direct measurement. Herein, a deembedding technique of odd number ports with two coupled interconnection lines is realized.

Ultimately, the proposed de-embedding method for both uncoupled and coupled interconnection lines is demonstrated in detail. The merits of our method are easily observed in Table 1, with a comparison of existing de-embedding methods and ours.

[Table 1.] A performance comparison of the existing de-embedding methods and our proposed approach

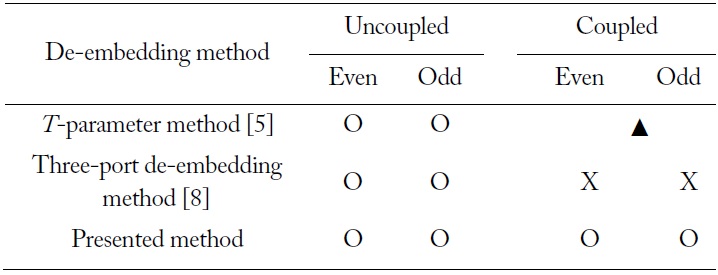
A performance comparison of the existing de-embedding methods and our proposed approach

In the uncoupled case, when the non-diagonal of the [S] matrix becomes null, as in (28), the formula of the [C] matrix is reduced to (29) and each term of the [C] matrix is described, as in (30) to (35).

It is interesting to see that the introduction of coupling for just two lines makes the formula extremely complicated in the de-embedding derivation.

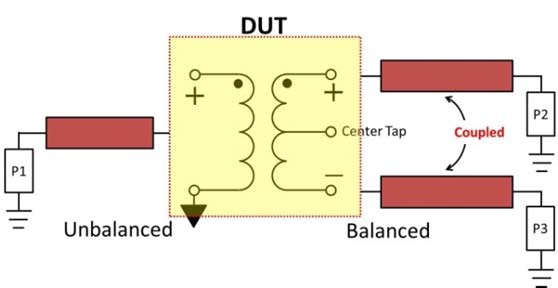
IV. CASE STUDY FOR COUPLED INTERCONNECTION LINES

The validation of the proposed method was performed based on the Agilent commercial circuit simulator—the Advanced Design System (ADS). In the circuit simulator, the microstrip line model is easily defined and the S-parameters of the model can be extracted in a short time. The proposed analysis of a three-port system with two ports coupled, as illustrated in Fig. 4, can be validated through the ADS circuit simulator.

[Fig. 4.] Multiport system with coupled interconnection lines. DUT=device under test.

The de-embedding method proposed for analyzing the characteristics of on-wafer metal–oxide–semiconductor field-effect transistor (MOSFETS) in [8] can no longer be effective for the coupled interconnection lines, as the non-diagonal elements in the S-matrix are null.

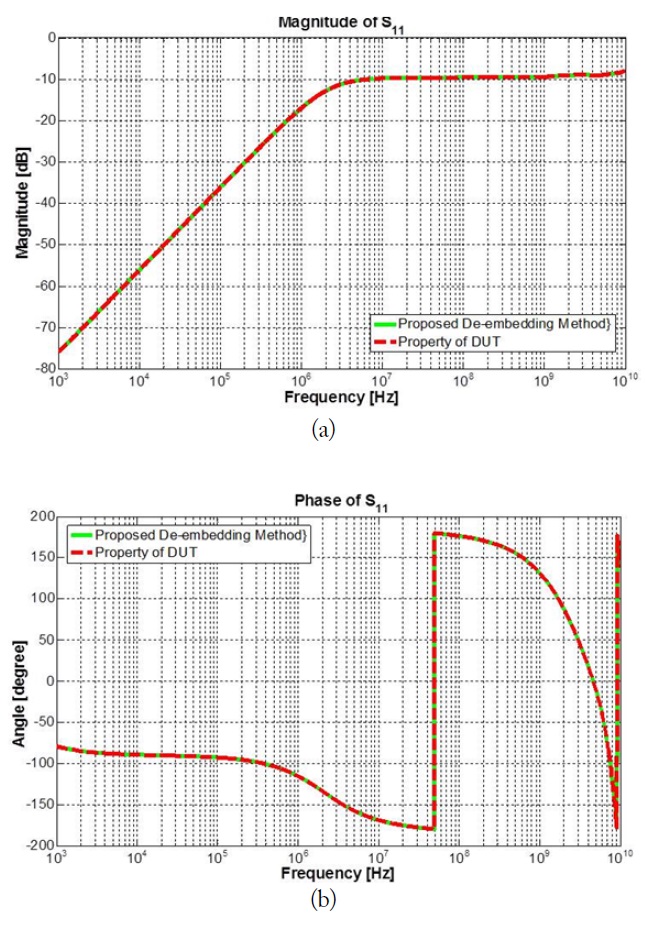
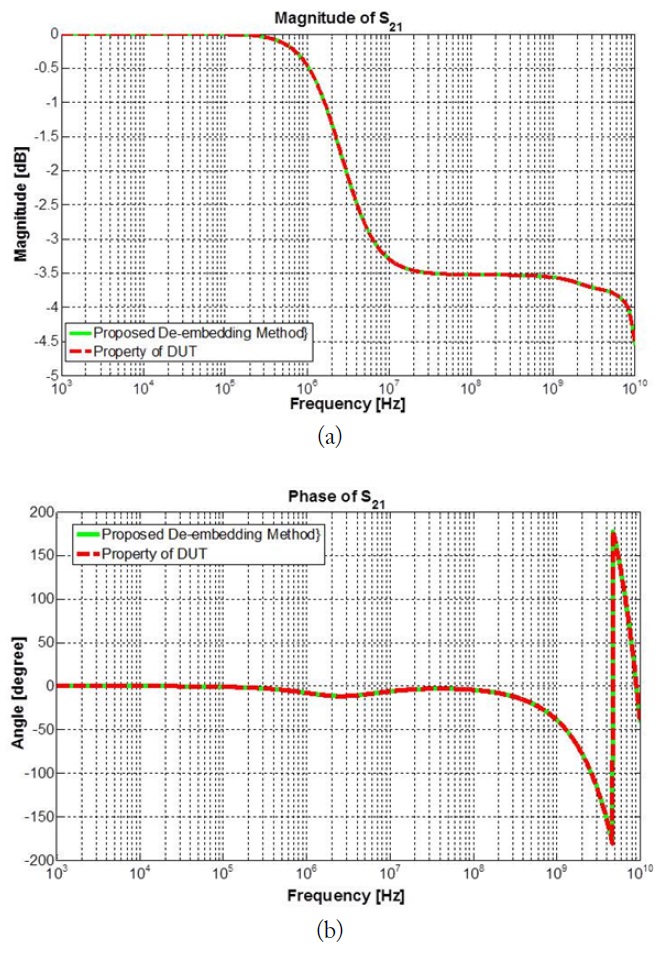
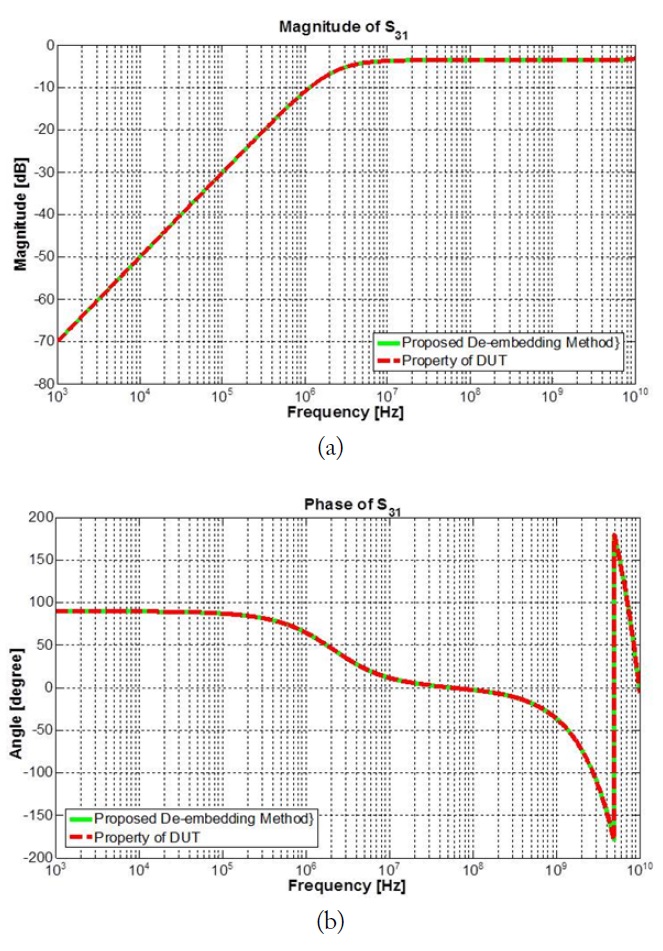
Although the result cannot be obtained by the method in [8], our proposed method worked well, and the extracted result matched the result from the simulation in a wide frequency range, as illustrated in Figs. 5–7. It validated the accuracy of our proposed de-embedding approach for coupled lines from a low frequency (1 kHz) to a high frequency (10 GHz). To shorten the calculating time, a code is made based on the mathematics language and is realized in MATLAB, which is a technical computing language used in engineering. The touchstone file constituting the property of the S-parameters can be easily handled to perform the de-embedding method in the code.

[Fig. 5.] (a) Magnitude and (b) phase comparison of the return loss at port 1 for the results of the proposed de-embedding method and the direct result from the device under test (DUT).

[Fig. 6.] (a) Magnitude and (b) phase comparison of the insertion loss between ports 1 and 2 for the results from the proposed deembedding method and the direct result from the device under test (DUT).

[Fig. 7.] (a) Magnitude and (b) phase comparison of the insertion loss between ports 1 and 3 for the results from the proposed deembedding method and the direct result from the device under test (DUT).

V. CONCLUSION

This paper proposed a de-embedding method for uncoupled and coupled interconnection lines based on the conversion of the S-matrix. The de-embedding manner for an even-port network based on the T-parameters is introduced, and the solution for both even- and odd-port networks based on our proposed method is addressed in detail through deriving the relationship of the S-parameters between available ports, which can be measured directly, and the port of the intrinsic DUT. A verification of the proposed method is also performed based on the spicelike commercial circuit simulator, and a good agreement is achieved between the proposed method and the validated results from the simulation.

참고문헌

1. Pozar D. M. 2005 Microwave Engineering
2. Speciale R. A. 1980 "Multiport network analyzers: meeting the design need," [Microwave Systems News] Vol.10
3. Lu H. C., Chu T. H. 2003 "Multiport scattering matrix measurement using a reduced-port network analyzer," [IEEE Transactions on Microwave Theory and Techniques] Vol.51 P.1525-1533
4. Van Hauwermeiren L., Botte M., De Zutter D. 1993 "A new de-embedding technique for on-board structures applied to the bandwidth measurement of packages," [IEEE Transactions on Components, Hybrids, and Manufacturing Technology] Vol.16 P.330-333
5. Frei J., Cai X. D., Muller S. 2008 "Multiport S-parameter and T-parameter conversion with symmetry extension," [IEEE Transactions on Microwave Theory and Techniques] Vol.56 P.2493-2504
6. Pu B., Kim T., Kim S., Kim J. H., Kim S., Nah W. 2013 "Estimation of transferred power from a noise source to an IC with forwarded power characteristics," [Journal of Electromagnetic Engineering and Science] Vol.13 P.233-239
7. Wojnowski M., Issakov V., Sommer G., Weigel R. 2012 "Multimode TRL calibration technique for characterization of differential devices," [IEEE Transactions on Microwave Theory and Techniques] Vol.60 P.2220-2247
8. Cho M. H., Huang G. W., Wu L. K., Chiu C. S., Wang Y. H., Chen K. M. 2005 "A shield-based three-port de-embedding method for microwave on-wafer characterization of deep sub-micron silicon MOSFETs," [IEEE Transactions on Microwave Theory and Techniques] Vol.53 P.2926-2934

이미지 / 테이블

[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ Fig. 1. ] A schematic for uncoupled N-port interconnections.
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ Fig. 2. ] A schematic to describe the uncoupled or coupled three-port network.
[ Fig. 3. ] An unbalanced three-port network consisting of a cascaded T-parameter.
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ Table 1. ] A performance comparison of the existing de-embedding methods and our proposed approach
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ ]
[ Fig. 4. ] Multiport system with coupled interconnection lines. DUT=device under test.
[ Fig. 5. ] (a) Magnitude and (b) phase comparison of the return loss at port 1 for the results of the proposed de-embedding method and the direct result from the device under test (DUT).
[ Fig. 6. ] (a) Magnitude and (b) phase comparison of the insertion loss between ports 1 and 2 for the results from the proposed deembedding method and the direct result from the device under test (DUT).
[ Fig. 7. ] (a) Magnitude and (b) phase comparison of the insertion loss between ports 1 and 3 for the results from the proposed deembedding method and the direct result from the device under test (DUT).