The present study aimed to develop a measurement tool for children's mathematical word problem solving abilities and to test its validity. Using the measurement tool, this study also examined the relationship among children's mathematical word problem solving abilities, ages, language abilities, and computation abilities. To this end, first, this study analyzed 58 mathematical word problem questions in the first grade elementary school math and activity books. Based on the analysis, this study developed a measurement tool for children's mathematical word problem solving abilities and then tested its validity by 310 children aged four through six. Second, this study assessed, by using the measurement tool, mathematical word problem solving abilities of 131 four through six year olds children in D and G cities, and then found out the relationships among children's mathematical word problem solving abilities, ages, language abilities, and computation abilities. Study results are as follows. First, the measurement tool for children's mathematical word problem solving abilities developed in this study was verified as a reliable and valid tool in terms of both adequacy of the items (passing rate, item-discrimination, and item-total correlation) and adequacy of the measurement tool (reliability and validity). Second, children's mathematical word problem solving abilities showed positive co-relations with children's ages, language abilities, and computation abilities. In addition, the results of stepwise regression analysis showed that children's language abilities affected most on children's mathematical word problem solving abilities, followed by children's computation abilities.
세계 각국들이 과학을 비롯한 모든 미래 산업기술 발달의 원천으로 수학의 중요성을 강조하면서 최근 우리나라도 수학교육의 중요성을 인식하여 2012년에「수학 선진화 방안」을 발표하고 적극적으로 수학교육의 질적 향상을 위한 정책을 확대하고 있다. 유아수학교육은 3-5세 누리과정 중 자연탐구영역의 ‘탐구하는 태도 기르기’와 ‘수학적 탐구하기’에 포함되어 놀이, 게임, 생활 속의 문제해결과 같은 여러 가지 활동을 통해 수학적 지식을 구성하고 생활 속의 여러 상황과 문제를 논리‧수학적으로 이해하고 해결하기 위한 기초능력을 기르는 것을 목표로 하고 있다(교육과학기술부, 보건복지부, 2013). 또한 수학교육 정책의 변화로 2013학년도 초등학교 1학년과 2학년에 다양한 활동과 스토리텔링으로 구성된 개정 교과서가 도입되었다. 개정된 초등학교 수학교과서는 실생활의 소재와 스 토리텔링을 활용하여 수학적 개념을 소개하고 실제적인 문제 상황을 통해 개념적 이해와 문제해결 전략을 사용하도록 함으로써 다른 학문 분야나 생활 속에서 융합적인 사고와 창의적인 사고를 하도록 하고 있다(교육과학기술부, 2013). 이와 같이 누리과정과 2009 개정 초등학교 교육과정은 교육부가 제시한「수학 선진화 방안」의 기본 방향인 생각하는 힘을 키우는 수학, 쉽게 이해하고 재미있게 배우는 수학과 그 맥락을 같이 하고 있다.
누리과정의 도입으로 취학 전 만 5세 유아의 대부분이 유치원과 어린이집에서 수학교육을 받고 초등학교에 진학하게 된다. 하지만 현재 유아교육은 기간 학제에 포함되지 않아 누리과정의 수학교육과 초등학교 1학년 수학교육간의 연계성이 부족하고, 누리과정의 성취기준 또한 다소 모호하게 기술되어 있어 현장교사들에게 혼란을 주고 있다. 뿐만 아니라, 초등 과정과는 달리 누리과정은 정규 교과서가 별도로 발행되지 않기 때문에 수학교육과 관련한 유아의 발달 수준 및 성취수준 평가에 지침이 될 수 있는 자료가 상대적으로 부족한 실정이다. 그러나 이러한 문제는 초등학교 교과서를 참고함으로써 다소나마 해결될 수 있으며 특히, 유아들이 초등학교 입학 후 가장 처음 접하게 되는 초등학교 1학년 수학 교과서와 익힘책에 관한 연구들은 유치원 수학교육의 내용 및 범위 선정에 도움을 줄 수 있다. 누리과정과 개정 초등 1학년 수학교과서에서 다루어지는 수의 범위(5세 누리과정: 1~20, 1학년 1학기 수학: 1~9)가 상당히 일치한다는 점, 그리고 초등 1학년 수학교과서 내용의 상향 조정이 필요하다는 지적(이정욱, 2014)을 종합해보면, 초등학교 1학년 수학교과서 분석연구는 유치원 교사들에게 보다 실질적인 자료를 제공해 줄 수 있을 것이라 여겨진다. 하지만 지금까지 초등학교 수학 교과서를 분석하였던 선행연구들(이대현, 2009; 이병옥, 안병곤, 2008; 이정재, 2004)은 대부분 2학년 이상의 교과서를 대상으로 이루어진 것으로, 이 연구들의 결과를 유치원 수학 교육에 직접적으로 적용하는 데에는 한계가 있다. 이러한 실정을 고려해 볼 때, 유아가 초등학교 입학 후 가장 처음 접하게 되는 초등학교 1학년 수학 교과와 익힘책에 관한 연구의 필요성이 대두된다.
개정된 초등학교 수학 교과서는 수학을 쉽게 이해하고 재미있게 배울 수 있도록 다양한 활동과 스토리텔링으로 구성된 것이 특징이다. 스토리텔링 수학교육은 수학적 상황이 포함된 이야기를 활용하여 수학적 내용 지식, 태도, 기술 등을 학습할 수 있도록 하는 접근 방법이다. 그러므로 언어가 수학학습에 핵심적인 역할을 하게 되며 유아들이 초등학교 입학 후 교육과정을 따라가기 위해서는 문장을 독해하고 이해하는 능력이 요구된다. 개정 교과서에서 제시되는 수학문제의 유형 또한 기존의 수식을 이용한 단순 계산보다는 더하기 빼기의 알고리즘(algorism)이 포함된 문장제의 비중이 높아지고 있는데, 이는 문장제가 스토리텔링 수학의 기본 구성요소이기 때문에 스토리텔링 비중 강화에 따른 당연한 결과로 볼 수 있다. 이와 같은 흐름에 발맞춰 유아들이 스토리텔링 수학에 대한 준비도를 갖추기 위해서는 그 어느 때보다도 수학 문장제에 대한 이해가 필요하다.
문장제(word problem)란 미지수의 양과 그 양들 사이의 관계를 덧셈이나 뺄셈이 포함된 단순한 장면 대신 말이나 문장으로 제시하는 문제이다(Riley et al., 1983). 수학 문장제는 수학적 요소와 언어적 요소가 모두 포함되어 있기 때문에 일상생활에서 비형식적 수학을 경험하는 유아에게 적합하며 수학의 궁극적인 목표 중 하나인 문제해결력을 기르는 데에도 중요한 역할을 한다. 일반적으로 수학에서 문장제 문제는 문제해결과 비슷한 의미로 사용되나, 문제해결은 좀 더 복잡하고 넓은 개념으로 이는 수학 문장제 문제 풀이를 통해 연습될 수 있다고 볼 수 있다(임효진, 2005). 김동일(2013)은 수학교과에서는 문제해결능력을 향상시키기 위해 문장제를 사용한다고 하였는데, 이는 문장제가 단순한 수학적 계산능력뿐만 아니라 일상생활에서 부딪히는 여러 가지 문제 상황과 관련되어 수학적 사고 발달에 많은 영향을 미치기 때문이다(송연숙, 황해익, 2000; Carpenter et al., 1984). 이러한 근거로 볼 때 유아들의 수학 학습은 구체적이고 다양한 상황을 통해 이루어져야 하며, 비록 수식으로는 동일하게 표현된다 할지라도 우리의 생활 속에는 덧셈과 뺄셈의 다양한 상황이 존재하므로 수와 연산 학습 또한 수식에 의한 더하기 빼기 학습보다는 다양한 맥락을 활용하여 이루어져야 한다.
수학 문장제를 분류하는 방법은 여러 가지가 있을 수 있지만 최근 초등학교 교과서를 분석한 선행연구들(백경선, 박순경, 권점례, 구영산, 2012; 이대현, 2009; 이병옥, 안병곤, 2008; 이정재, 2004)에서는 수학 문장제를 의미론적 관점에서 분류하는 것이 선호되고 있다. 이는 문제를 파악하는 방법을 일치시키기 위하여 문제에 기술된 행위나 관계의 유형에 따라 분류하는 것이 적절하기 때문이다(Carpenter et al, 1999). 즉, 학생들이 수학 문장제를 접할 때 우선 문장제의 의미론적 구조를 파악하고, 그런 다음 수학 문장제에 내포된 연산의 개념적 이해를 바탕으로 문제해결에 필요한 연산을 결정함으로서 최종적으로 문제를 해결하게 되므로, 의미론적 관점의 분류가 중요시 되고 있다.
유아의 수학 문장제 문제해결력과 연령에 관련된 선행연구들(송연숙, 2002; 홍혜경, 2013; Fuson, 1992)에 따르면 4∼6세 유아들은 상황적 맥락을 포함한 더하기와 빼기의 수학 문장제 문제를 해결할 수 있으며 유아의 수학 문장제 문제해결력은 연령이 증가함에 따라 발달하고 있음을 밝히고 있다. 하지만 초등학교 입학 후 학년이 증가 할수록 수학 문장제 문제 해결에 있어, 문제를 읽고 이해하는데 필요한 읽기 이해능력, 수에 대한 기본 개념 및 계산능력 등의 부족으로 어려움을 겪고 있으며, 이러한 어려움으로 인한 누적된 학습곤란 때문에 수학 문장제 문제해결에 더욱 어려움을 느끼고 있다(김미진, 1993). 이는 수학 문장제 문제해결의 문제점이 연령이 증가함에 따라 지속되는 것임을 시사한다. 따라서 유아들이 초등학교에 잘 적응하고 추후 학업에서도 높은 성취를 얻기 위해서는 이러한 문제에 대한 구체적인 해결책이 요구되며, 유아의 연령과 수학 문장제 해결능력과의 관계를 살펴볼 필요성이 제기된다.
수학 문장제 문제의 해결과정은 크게 문장 독해과정과 연산과정으로 나누어져 있으며 유아는 문장제 문제를 풀 때 그와 유사한 수식의 문제를 풀 때보다 더 많은 오류를 범하고 있다(Carpenter, Kepner, Corbitt, Lindquist, & Reys, 1980). 따라서 수학 문장제 문제 해결 과정에서의 실패가 문장 독해과정과 계산과정 중 어디에 기인하는지 밝히는 연구는 그 자체로 중요하다. 예를 들어, 유아는 종종 ‘3+2는 얼마인가?’라는 문제를 이와 유사한 수학 문장제 문제인 ‘철수가 사탕 세 개를 가지고 있고, 영희는 두 개를 가지고 있다면, 모두 몇 개의 사탕을 가지고 있는가?’ 보다 더 정확하게 풀 수 있다. 이와 같은 현상이 나타나는 이유에 대해 선행연구에서는 수학 문장제 문제에서 읽기능력이 우수한 아동이 읽기 능력이 떨어지는 아동에 비해 수행률이 높으며(Moyer, 1984), 읽기 성적이 높아짐에 따라 문장제의 정반응률도 높다(Marshall, 1995)는 결과와 문장제 해결에서 문제이해과정의 오류 발생률이 계산과정의 오류 발생률보다 높다(이병옥, 안병곤, 2008; Mayer, 1983)고 하였다. 이들의 연구 결과는 언어적 능력이 수학 문장제 해결에 가장 중요한 변인임을 시사한다. 반면 수학 문장제 문제의 해결의 어려움이 수학적인 능력에 기인한다는 연구들(송연숙, 2002; 유승구, 1990)과 수식을 사용한 연산문제의 반복 학습을 한 경우 수식을 이용한 계산 문제는 잘 해결하지만 문장제 문제에서는 오히려 어려움을 겪는다고 밝힌 연구도 있다(Carpenter, Kepner, Corbitt, Lindquist, & Reys, 1980). 이상에서 살펴본 선행 연구들은 유아의 문장제 문제해결 오류와 관련하여 상반된 결과를 보여주었다. 따라서 수학 문장제 해결과정에서 언어적인 능력과 수학적인 능력 중 어느 것이 수학 문장제 수행에 더 영향을 미치는지를 밝히는 추가적인 연구가 필요할 것으로 여겨진다.
실제 교육현장에서는 언어적 요인과 수리적 요인이 복합적으로 내재되어 있어, 이에 대한 복합적인 문제해결력을 요하는 문장제 문제의 해결에 유아들이 많은 어려움을 느끼고 있다(이봉주, 문승호, 2007). 수학 문장제 문제는 유아의 발달하는 계산 기술과 이러한 기술을 실생활 상황에 적용하는 것 사이에 중요한 가교 역할(Briars & Larkin, 1984)을 한다. 하지만 유아 수학 문장제와 관련된 선행 연구들에는 문장제 문제 유형에 따른 해결능력 발달과 관련된 연구(홍혜경, 2009), 문장제 해결능력에 관련된 변인 연구(송연숙, 황해익, 2000), 연령에 따른 수학 문장제 해결과 관련된 연구(송연숙, 2002; 송연숙, 황해익, 2000; 홍혜경, 2009)등으로 연구 수가 많지 않다. 또한 유아 수학 문장제와 관련한 연구들은 대부분이 초등학생 이상의 아동을 대상으로 진행되어, 연구 결과를 유치원 수학교육에 적용하기에는 무리가 있다. 한편 유아 수학 문장제 선행연구들(송연숙, 2002; 송연숙, 황해익, 2000; 홍혜경, 2009)에서 사용된 수학 문장제 검사 도구들은 외국의 연구를 참고로 제작되었기 때문에 유아가 형식적 교육을 받으면서 가장 먼저 접하게 되는 초등학교 1학년 수학교과서의 문장제 문제와는 차이가 있어 유‧초 연계를 강조하는 현재 수학 교육 흐름에 부적절한 면이 있을 수 있다. 따라서 초등학교 1학년 수학 교과서와 익힘책에 사용된 의미구조와 소재를 토대로 유아 수학 문장제 문제해결력 검사 도구를 제작하여, 유아가 수학 문장제 문제해결력을 어떻게 발달시켜 나가는지를 이해하고 문제해결 과정에서 그들이 보이는 어려움의 원인을 규명하는 것은 매우 의미가 있을 것이다.
이에 본 연구는 초등학교 1∼2학년군 1학년 수학 교과서와 익힘책의 수학 문장제 문제를 의미론적 관점에서 분류하고 수학 문장제에 사용된 소재를 알아본 후 이를 바탕으로 유아 수학 문장제 문제해결력 검사를 개발할 것이다. 이렇게 제작된 검사도구를 사용하여 유아의 수학 문장제 문제해결력과 연령, 언어능력, 수와 연산능력과의 상관관계 그리고 어떤 변인이 수학 문장제 해결에 차이를 보이게 하는지 그 상대적 설명력을 살펴보고자 한다. 이를 통하여 유아의 수학 문장제 문제해결에 있어 차이를 유발시키는 변인이 무엇인지를 파악할 수 있을 것이다. 뿐만 아니라 유아의 수학 문장제 문제해결 능력의 향상과 유아교사들에게 수학 교육의 내용과 범위 등 수학 교육의 방향을 제시해줌으로써 유아 수학교육 및 추후 초등학교 수학교육에 대한 기초자료와 시사점을 제공하고자 한다.
이러한 연구목적을 달성하기 위하여 선정된 연구문제는 다음과 같다.
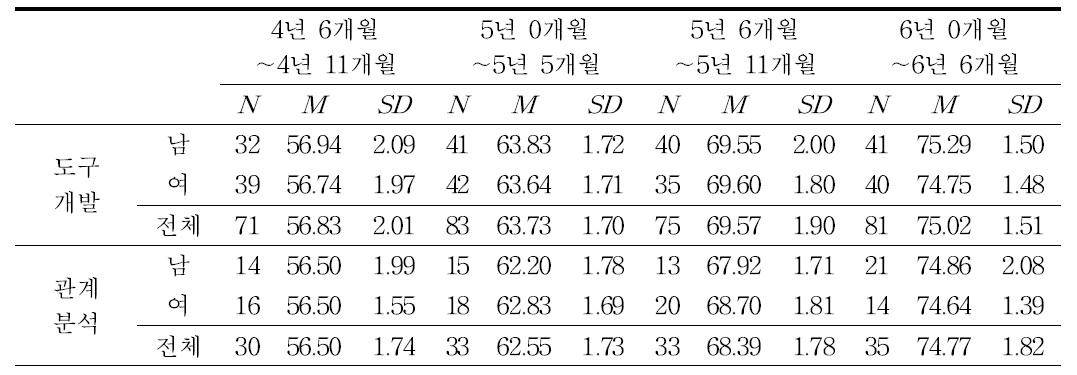
본 연구는 D광역시와 G도에 소재하는 유치원과 어린이집에 다니는 만 4세에서 학령 전 6세까지의 유아를 대상으로 실시되었다. 구체적인 연구대상의 구성은 표 1과 같다. 연구대상은 선행연구들(송연숙, 2002; 홍혜경, 2013; Fuson, 1992)에 따라 수학 문장제를 풀 수 있는 4세부터 학령 전 6세까지의 유아로 선정하였고 짧은 시기 동안에 변화의 폭이 크게 나타나는 유아기의 특성을 고려하여(김소연, 2012; 최혜진, 이혜은, 2005) 월령 구분을 6개월 단위로 정하였다.
[<표 1>] 연구대상 유아의 성별 평균 개월 수 및 표준편차
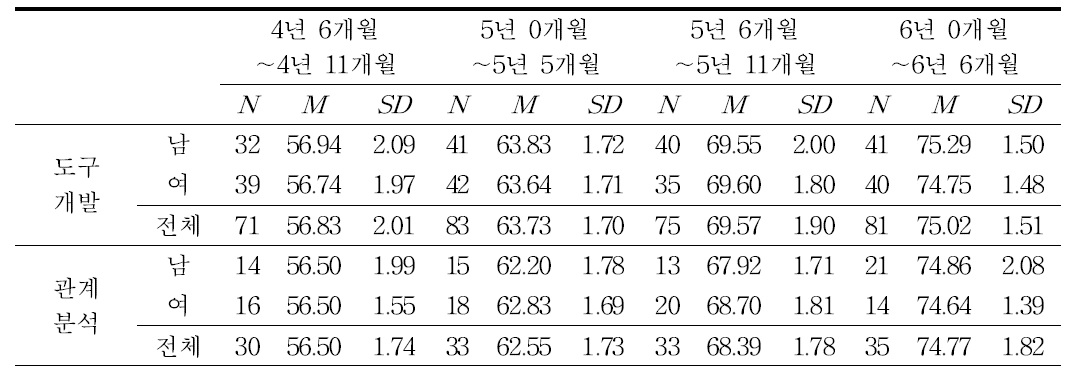
연구대상 유아의 성별 평균 개월 수 및 표준편차
1) 유아 수학 문장제 문제해결력 검사도구
본 연구에서 사용한 유아 수학 문장제 문제해결력 검사도구는 초등학교 1∼2학년군 1학년 수학 교과서와 수학 익힘책에 수록된 수학 문장제 문제의 의미 유형, 실생활 소재를 분석한 후, 그 분석 결과를 바탕으로 제작된 검사도구이다. 총 20개의 검사문항 중 덧셈식에 합병(결합) 7문항, 첨가(증가) 3문항, 뺄셈식에 제거 8문항, 비교 2문항으로 구성하였다. 덧셈과 뺄셈의 역연산 관계는 초등학교 1학년 아동에게도 가르치기 어렵다는 백경선, 박순경, 권점례, 구영산(2012)의 연구를 참고하여 본 연구 검사 문항에 포함하지 않았다. 검사에 사용된 수의 범위는 덧셈의 경우 합이 5이상 10이하로 뺄셈의 경우는 피감수가 5이상 10이하로 하였으며, 정답일 경우 1점, 오답일 경우 0점을 주도록 되어있으며 총점은 20점이다. 본 연구의 신뢰도 Cronbach
2) 수와 연산능력 검사도구
유아의 수와 연산능력을 측정하기 위해 황해익과 최혜진(2007)의 유아 그림수학능력 검사도구 중 수와 연산영역의 검사만을 사용하였다. 수와 연산능력 검사는 수세기, 숫자 인식의 수 개념 10문항과 더하기와 빼기의 수‧연산 8문항으로 구성되었으며, 각 문항은 정답일 경우 1점, 오답일 경우 0점을 주도록 되어있으며 총점은 18점이다. 본 연구의 신뢰도 Cronbach
3) 언어능력 검사도구
언어능력은 적절하고 의미 있는 문장을 이해하고 만들어내는 능력으로 다른 사람의 말을 듣고 그 말에 사용된 낱말, 낱말의 배열순서, 문장 내에 포함된 문법형태소 그리고 구문구조 등에 의존하여 문장을 이해할 수 있는 능력을 의미 한다(정재은, 2013; 조서희, 2012). 본 연구에서는 어휘력, 문법형태소, 구문구조, 의미를 분석한 내용을 언어능력으로 정의하였다.
(1) 그림 어휘력 검사(PPVT-R)
그림 어휘력 검사는 김영태, 장혜성, 임선숙, 백현정(1995)이 ‘Peabody Picture Vocabulary Test Revised(PPVT-R)’를 토대로 한국에서 제작한 검사 도구를 사용하였다. 이 도구는 그림을 이용하여 2세 0개월부터 8세 11개월 유아의 수용어휘력을 측정하는 것으로 국내에서 표준화 과정을 거쳤다. 문항 내용 구성은 품사별로 명사(57%), 동사(20%), 형용사(12%), 부사(1%)등을 포함하고 있고, 범주별로는 동물, 건물, 옷, 음식, 가구, 가정용품, 신체 부위, 직업, 도형, 식물, 학교 및 사무실의 비품, 가구 및 장치, 악기, 교통기관 등으로 총 112개의 문항으로 구성되어 있다. 각 문항은 정답일 경우 1점, 오답일 경우 0점을 주도록 되어있으며 총점은 112점이다. 본 연구의 신뢰도 Cronbach
(2) 구문의미이해력 검사(TOLD-2)
구문의미이해력 검사는 배소영, 임선숙, 이지희, 장혜성(2004)이 ‘Test of Language Development-2, Primary(TOLD-2)’를 타당화 작업을 통해 한국 실정에 적합하게 개발한 검사 도구를 사용하였다. 이 도구는 만 4세에서 9세 수준의 구문의미이해력을 측정하는 것으로 문법적인 면과 의미적인 면을 측정할 수 있도록 문항이 구성되어 있으며, 발달적으로 이해하기 쉬운 문항에서 어려운 문항으로 배열되어 있다. 총 57개의 검사문항 중 문법 형태소에 초점이 맞춰진 경우가 10문항, 구문 구조적 특성에 초점이 맞춰진 경우가 28문항, 의미에 초점이 맞춰진 경우가 19문항이다. 본 검사는 대상 유아에게 그림 자료를 제시한 후에 목표 문장을 들려 준 후 3개의 그림 중 하나의 그림을 가리키도록 하는 방법으로 정답일 경우 1점, 오답일 경우 0점을 주도록 되어있으며 총점은 57점이다. 본 연구의 신뢰도 Cronbach
3. 유아 수학 문장제 문제해결력 검사 개발을 위한 초등학교 1학년 수학 교과서 및 익힘책 분석
유아 수학 문장제 문제해결력 검사를 개발하기 위하여 초등학교 1 학년 수학 교과서와 수학 익힘책에 제시된 ‘수와 연산’ 영역의 수학 문장제의 문장 표현과 실생활의 소재 활용 및 덧셈, 뺄셈의 계산식별로 주로 사용하는 낱말이나 어휘 패턴을 분석하였다. 초등학교 1학년 수학 교과서와 익힘책에 제시된 수학 문장제 문항은 수학1의 18문항, 수학2의 40문항으로 총 58문항이며 수록된 모든 문항(58문항)을 분석 대상으로 하였다. 수학 교과서와 익힘책의 수학 문장제 문항을 계산식별로 분류하면, 표 2와 같다.
[<표 2>] 1학년 수학 문장제 문항의 계산식에 따른 빈도 분석

1학년 수학 문장제 문항의 계산식에 따른 빈도 분석
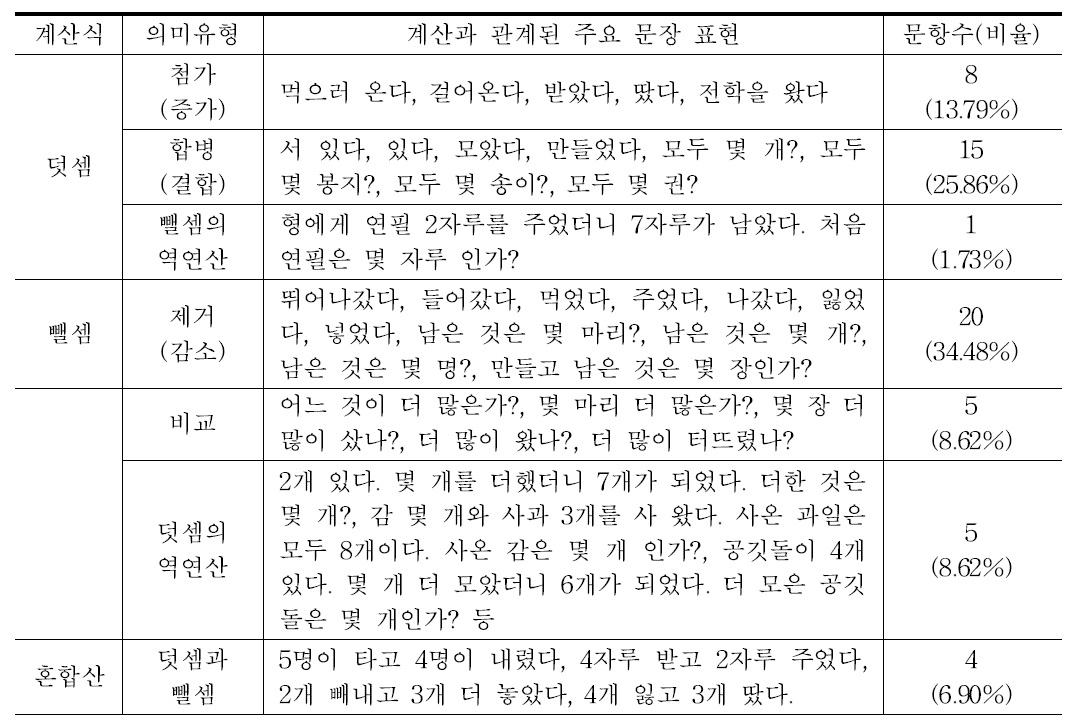
또한 초등학교 1학년 수학 교과서와 익힘책에 제시된 문장제 58문항에 사용된 주요 낱말이나 어휘를 첨가, 합병(결합), 뺄셈의 역연산, 제거, 비교, 덧셈의 역연산의 6가지 의미 유형에 따라 분석하였다. 수학 문장제를 분석하는 방법은 여러 가지가 있을 수 있지만, 문제를 파악하는 방법을 일치시키기 위해 문제에 기술된 행위나 관계의 유형에 따라 분류하는 것이 적절하다는 Carpenter 외(1999)의 연구결과와 최근 초등학교 교과서를 분석한 다수의 선행연구들(백경선, 박순경, 권점례, 구영산, 2012; 이대현, 2009; 이병옥, 안병곤, 2008; 이정재, 2004)을 따라 본 연구도 의미론적 관점으로 교과서 문장제 문제를 분석하였다. 분석결과는 표 3과 같다.
[<표 3>] 1학년 수학 문장제 문항의 계산식별 주요 표현
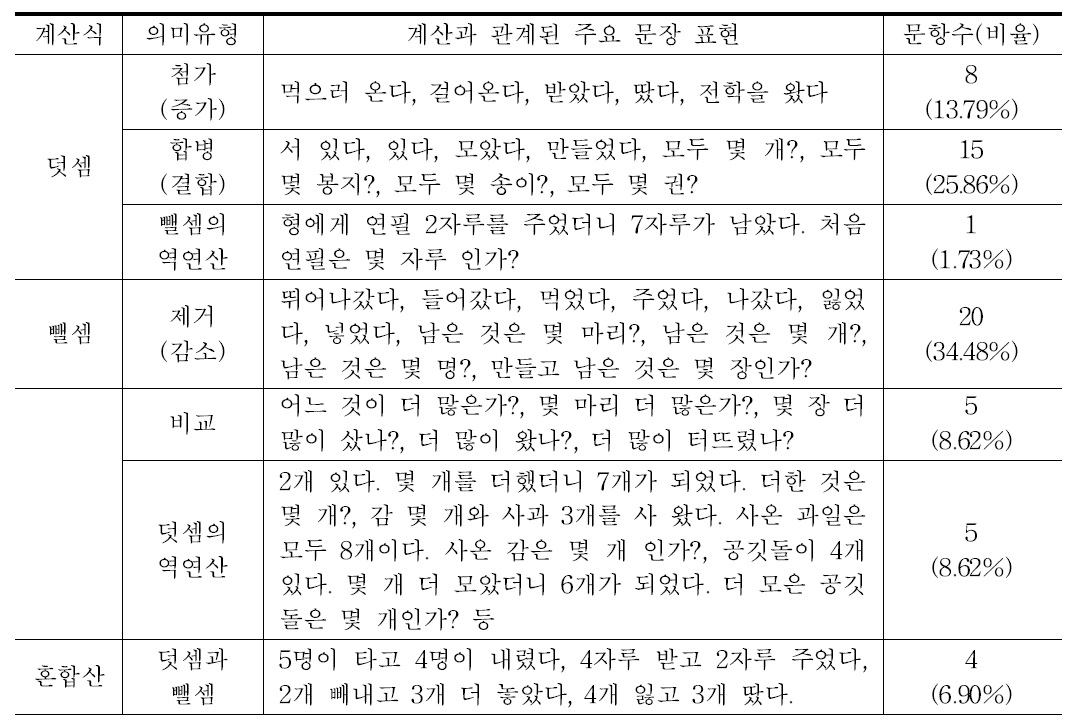
1학년 수학 문장제 문항의 계산식별 주요 표현
덧셈과 관련된 24문항 중 합병(결합) 유형이 15문항으로 가장 많고 첨가(증가) 유형이 8문항, 뺄셈의 역연산 유형이 1문항 순으로 나타났으며, 뺄셈과 관련된 30문항 중 제거 유형이 20문항, 비교 유형이 5문항, 덧셈의 역연산 유형이 5문항 순으로 나타났다.
덧셈의 문장 표현은 ‘모두 몇 ○○입니까?’, ‘더했더니’ 등과 같은 어휘를 주로 사용하고 있으며, ‘있다’, ‘오다’, ‘사다’, ‘넣다’, ‘받다’, ‘읽다’, ‘왔다’, ‘땄다’, ‘모았다’, ‘만들었다’, ‘터뜨렸다’ 등 실생활 언어와 동물의 마리 수나 물건의 개수의 합을 구하는 문항이 많았다. 뺄셈의 문장 표현은 ‘남아 있는 ○○은 몇 ○○입니까?’, ‘몇 개 남았습니까?’ ‘더 많습니까?’ 등과 같은 어휘를 주로 사용하고 있으며, ‘나갔다’, ‘들어갔다’, ‘터뜨렸다’ 등 실생활 언어와 남은 동물이나 물건의 개수, 비교에 대한 차를 구하는 문항이 많았다. 문장 표현을 정리하면 집합의 증가나 감소를 나타내는 ‘온다’, ‘받았다’, ‘땄다’, ‘갔다’, ‘먹었다’, ‘주었다’, ‘잃었다’, ‘남은 것은?’ 등과 집합의 합병이나 비교를 나타내는 ‘모았다’, ‘모두 몇 개?’, ‘어느 것이 더 많은가?’ 등과 같은 낱말이나 어휘를 많이 사용하고 있다.
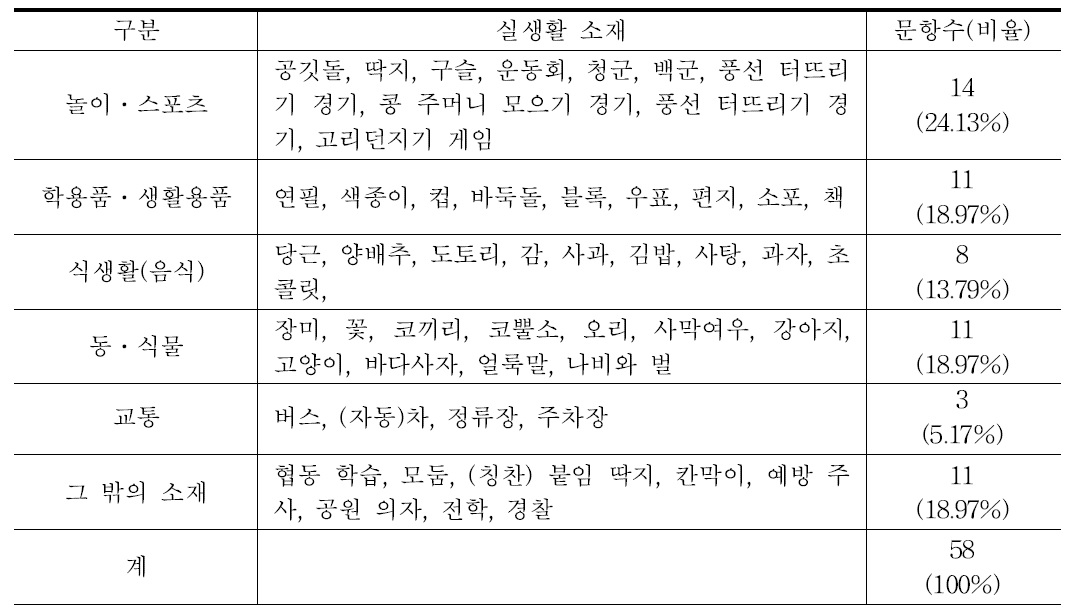
수학 문장제에 사용된 소재는 선행연구들(노현옥, 정은실, 2005; 이병옥, 안병곤, 2008)에 따라 분석하였다. 구체적으로, 실생활 소재를 같은 유형끼리 범주화하여 놀이‧스포츠, 학용품‧생활용품, 식생활(음식), 동‧식물, 교통, 그 밖의 소재, 총 6개 유형으로 분류하여 유형에 따른 활용 빈도를 분석하였고, 그 결과는 표 4와 같다.
[<표 4>] 1학년 수학 문장제 문항의 실생활 소재 활용 빈도 분석
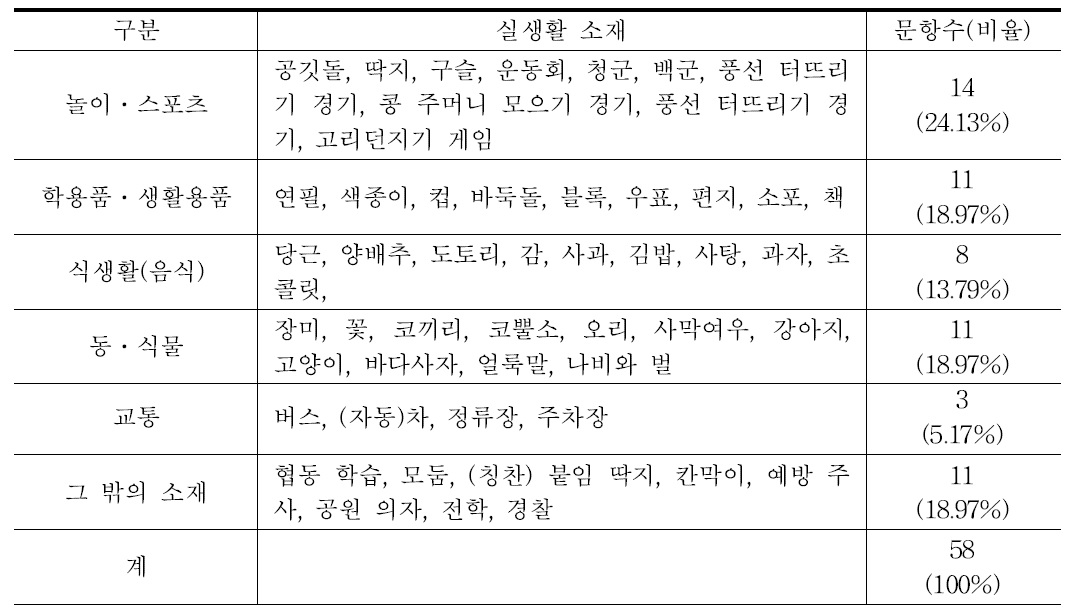
1학년 수학 문장제 문항의 실생활 소재 활용 빈도 분석
초등학교 1학년 수학 교과서와 익힘책에 제시된 문장제 58문항의 소재로는 놀이‧스포츠가 14문항(24.13%)로 가장 많고, 학용품‧생활용품, 동‧식물, 그 밖의 소재가 각각 11문항(18.97%), 식생활(음식) 8문항(13.79%), 교통 3문항(5.17%) 순으로 이와 관련된 52개의 실생활 소재를 사용하고 있으며, 운동회의 각종 경기와 게임, 협동 학습과 (칭찬)붙임 딱지 등과 같은 학교생활 관련 소재는 반복적으로 자주 사용되고 있다.
이상에서 분석한 결과를 바탕으로 본 연구는 다음과 같이 유아 수학 문장제 해결력 검사도구를 구성하였다. 의미유형 및 문항수는 덧셈식에 합병(결합) 7문항, 첨가(증가) 3문항, 뺄셈식에 제거 8문항, 비교 2문항으로 하였고, 각 유형별 문항 수의 비율은 초등 1학년 교과서와 비슷하게 구성하였다. 그러나 덧셈과 뺄셈의 역연산 관계는 초등학교 1학년 아동에게도 가르치기 어렵다는 선행연구(백경선, 박순경, 권점례, 구영산, 2012)를 참고하여 본 연구 검사 문항에 포함하지 않았다. 유형 및 문항수와 마찬가지로, 문항 소재와 주요 문장표현도 초등학교 1학년 교과서와 익힘책에서 사용된 것으로 구성하였다. 마지막으로 본 연구의 유아 수학 문장제 해결력 검사도구에 사용된 수의 범위는 덧셈은 합이 5이상 10이하로, 뺄셈은 피감수가 5이상 10이하로 한정하였다. 이는 한자리 수의 구체물을 조작하여 덧셈과 뺄셈의 기초를 형성하도록 제시하고 있는 누리과정 해설서(2013)를 참고로 하였다.
1) 예비연구
본 연구에 앞서 2014년 6월 9일∼18일 동안 예비연구를 실시하였다. 연구도구의 내용 타당성을 확보하기 위하여 대학에서 유아수학교육을 강의하는 교수 2명과 석사학위 이상 경력 3년 이상의 유치원 현장교사 3명에게 검토를 의뢰하였으며, 그 결과 연구도구에서 다룬 수의 범위, 수준, 제시방법에 대한 문제점이 제기되지 않아 이를 그대로 사용하였다. 또한 연구도구의 과제가 유아에게 적합한지를 검토하기 위해 본 연구에 참여하지 않는 비슷한 배경의 연령별 유아 5명씩 20명에게 실시한 결과, 다수의 유아들이 초등학교 1학년 수학 교과서와 수학 익힘책에서 사용하고 있는 소재인 (칭찬) 붙임딱지와 공깃돌을 모르는 것으로 나타나 이를 스티커와 사탕으로 각각 변경하였다. 또한 연구 보조원은 유아 교육을 전공하고 있는 대학원생 6명을 선정하여 과제의 제시방법, 질문내용, 평정방법, 관찰 및 기록 작업 등에 대한 설명과 시범을 통한 보조원 훈련을 3회에 걸쳐 실시하였다. 예비연구를 통해 유아와의 관계형성, 문제 제시 방법, 진행요령 등을 시행하는 반복 경험을 하도록 하였으며, 도구적합성 검토 작업에 참여한 유아 20명을 대상으로 평정자간 일치도를 산출한 결과 97%로 나타났다.
2) 본 연구
본 연구의 자료 수집은 2014년 6월 20일∼7월 15일까지 실시하였다. 검사는 주위 환경에 방해받지 않는 조용한 교실이나 특별활동 교실에서 유아에게 검사 방법에 대해 충분히 설명한 후, 일대일 개별 면담형식으로 이루어졌다. 책상 위에 색깔 단추, 숫자카드를 제시하고, 유아에게 문제를 풀기 위해 자신이 사용하고 싶은 것을 사용할 수 있다고 설명한 뒤 문제해결을 위해 이를 자유롭게 사용하도록 하였다. 연구자와 연구보조원은 제시되는 문제를 읽어주고, 유아가 과제를 수행하는 동안 유아의 반응을 관찰하고 기록하였다. 단, 유아가 요청하면 문제를 한 번 더 읽어주었다.
1) 유아의 수학 문장제 문제해결력 검사도구의 타당화
유아 수학 문장제 문제해결력 검사도구의 문항양호도를 알아보기 위하여 각 문항별 문항통과율과 문항변별도, 내용단일성을 산출하였다. 문항통과율은 각 문항에 올바르게 답한 유아의 비율을 빈도와 백분율로 산출하였다. 문항변별도는 검사 총점을 기준으로 상위 27%와 하위 27%를 상‧하집단으로 구분하여(Kelly, 1939), 상‧하집단 간 평균에 유의미한 차이가 있는지를 각 문항별로 독립표본
2) 유아의 수학 문장제 문제해결능력과 연령, 언어능력, 수학능력간의 관계와 상대적 영향력 분석
유아 수학 문장제 문제해결력 검사를 실시한 후 그 결과를 중심으로 유아 수학 문장제 해결능력과 연령, 언어능력, 연산능력간의 관계를 알아보기 위하여 Pearson의 상관분석을 실시하였다. 유아의 연령, 언어능력, 연산능력이 유아의 수학 문장제 해결능력에 미치는 상대적 영향력을 살펴보기 위하여 유아의 연령, 언어능력, 연산능력변인을 독립변인으로 유아 수학 문장제 해결능력을 종속변인으로 하여 단계적 다중회귀분석(Multiple regression analysis)을 실시하였다.
모든 통계처리는 SPSS 19.0 프로그램을 이용하여 분석하였다.
1) 유아 수학 문장제 문제해결력 검사도구의 문항 양호도
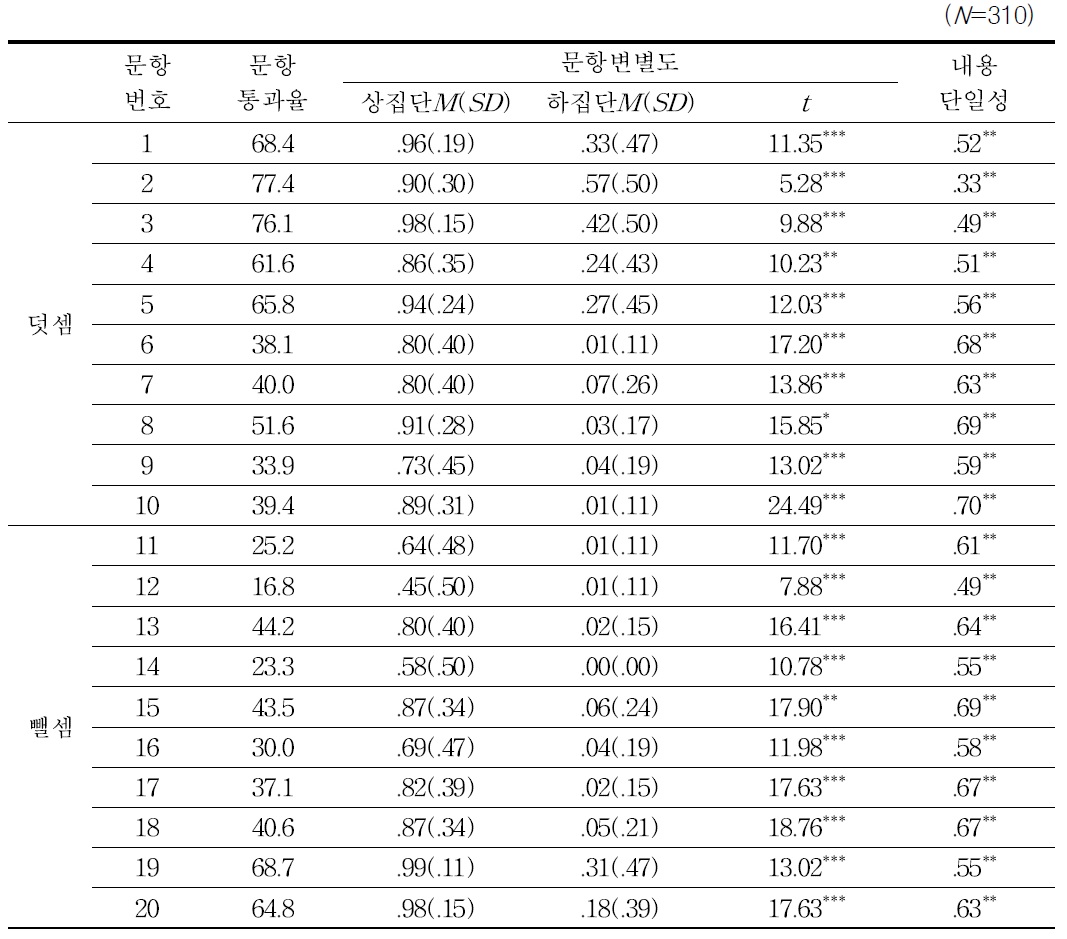
유아 수학 문장제 문제해결력 검사도구의 문항 양호도를 알아보기 위하여 문항통과율과 문항변별도, 내용단일성을 산출한 결과는 표 5와 같다.
[<표 5>] 유아 수학 문장제 문제해결력 검사도구의 문항 통과율과 문항 변별도
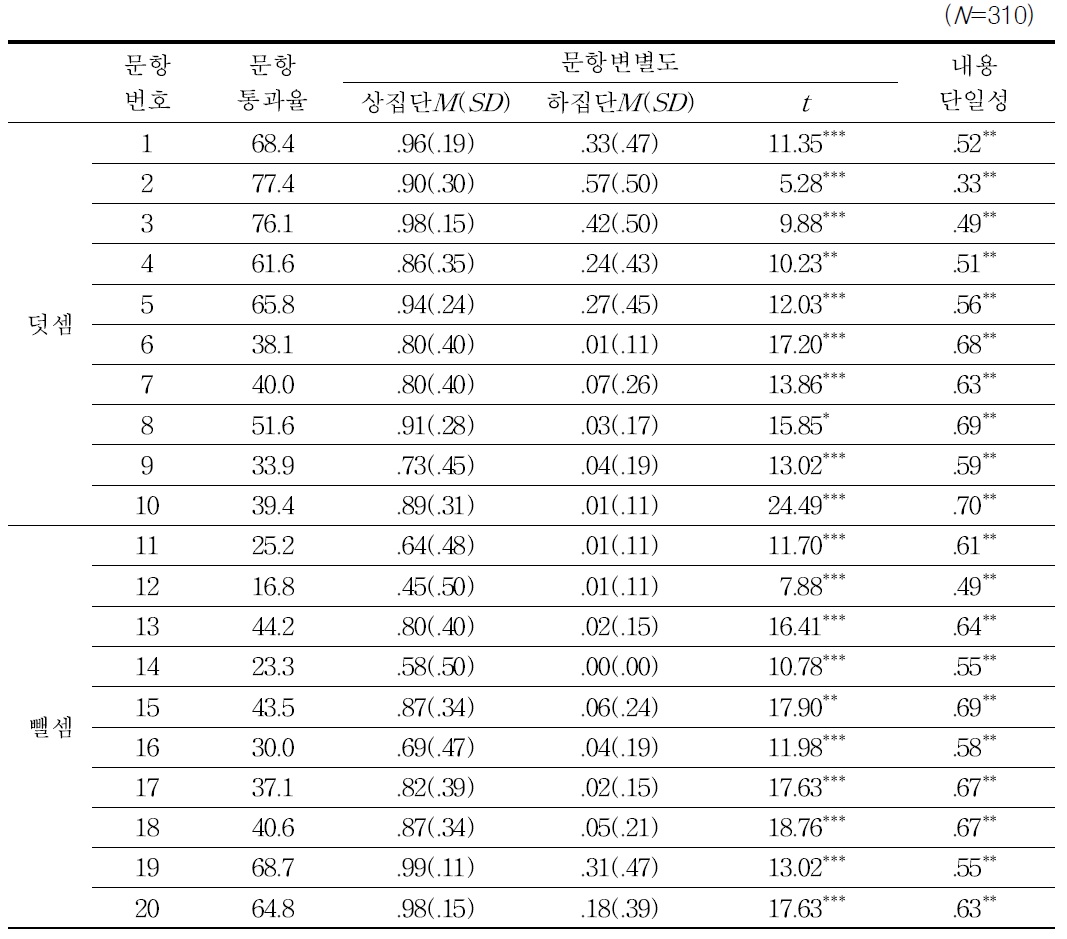
유아 수학 문장제 문제해결력 검사도구의 문항 통과율과 문항 변별도
문항통과율은 16.8에서 77.4%정도로 나타나, 검사도구에 난이도별 문항이 골고루 포함되어 있음을 알 수 있다. 문항변별도는 모든 문항에서 상집단의 평균이 하집단의 평균보다 높았으며, 이러한 평균의 차이가 유의미한 것으로 나타났다. 이는 유아 수학 문장제 문제해결력 검사의 각 문항들이 전체적으로 유아의 문장제 문제해결력을 잘 변별할 수 있음을 의미한다. 내용단일성은 각 문항 점수와 유아수학 문장제 문제해결력 검사 총점과의 상관이 .33에서 .69 사이로 비교적 높게 나타났다.
2) 유아 수학 문장제 문제해결력 검사도구의 검사 양호도
(1) 신뢰도
유아 수학 문장제 문제해결력 검사도구의 신뢰도를 문항 내적합치도인 Cronbach
[<표 6>] 유아 수학 문장제 문제해결력 검사도구의 문항 내적합치도

유아 수학 문장제 문제해결력 검사도구의 문항 내적합치도
(2) 타당도
① 구인타당도
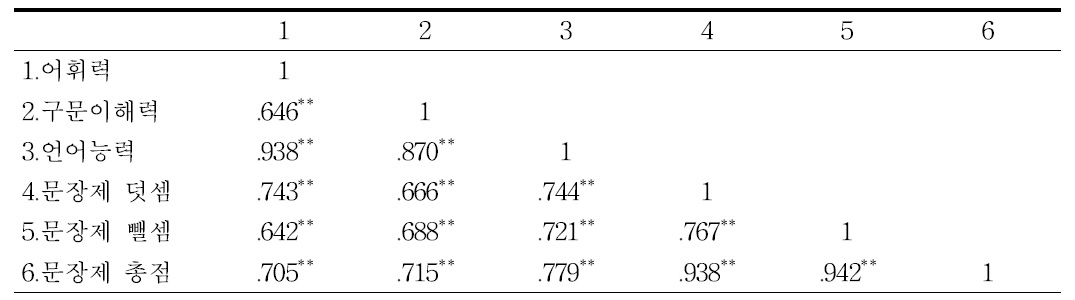
유아 수학 문장제 문제해결력 검사도구의 구인타당도를 알아보기 위하여 하위영역 간의 상관 계수를 산출한 결과는 표 7과 같으며, 각 하위영역 및 총점 간 상관은 .776에서 .944로 비교적 높게 나타났다.
[<표 7>] 유아 수학 문장제 문제해결력 검사도구의 하위영역 간의 상관계수

유아 수학 문장제 문제해결력 검사도구의 하위영역 간의 상관계수
② 공인타당도
유아 수학 문장제 문제해결력 검사도구의 공인타당도를 알아보기 위하여 유아 그림수학능력 검사(황해익, 최혜진, 2007)의 수와 연산영역을 실시하여 상관계수를 산출한 결과는 표 8과 같이 덧셈영역 .721, 뺄셈영역 .719, 총점 .764로 통계적으로 유의한 상관관계를 나타냈다. 이에 유아 수학 문장제 문제해결력 검사는 공인타당도를 갖춘 검사도구임이 확인되었다.

유아 수학 문장제 문제해결력 검사도구의
2. 유아 수학 문장제와 연령, 언어능력, 수학능력간의 관계와 설명력
1) 유아의 연령과 유아 수학 문장제와의 관계
유아의 연령과 유아 수학 문장제와의 관계를 알아보기 위해 Pearson의 적률상관분석을 실시한 결과, 표 9와 같다. 유아의 연령은 수학 문장제 덧셈(
[<표 9>] 유아의 연령과 유아 수학 문장제와의 상관관계

유아의 연령과 유아 수학 문장제와의 상관관계
2) 유아의 언어능력과 수학 문장제와의 관계
유아의 언어능력과 유아 수학 문장제와의 관계를 알아보기 위해 Pearson의 적률상관분석을 실시한 결과, 표 10과 같다. 유아의 어휘력은 수학 문장제 덧셈(
[<표 10>] 유아의 연령과 유아 수학 문장제와의 상관관계
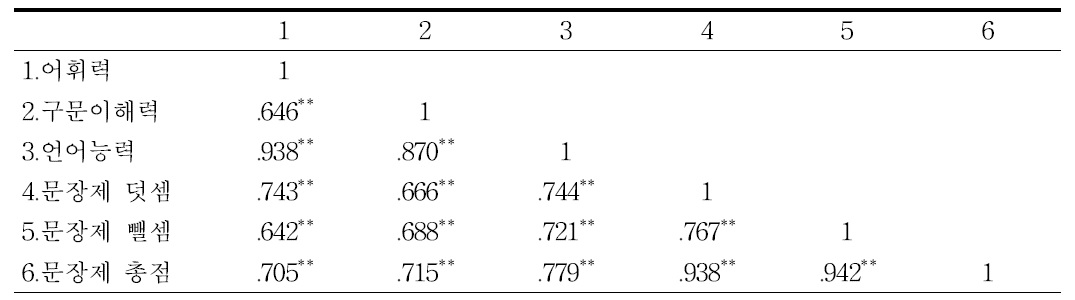
유아의 연령과 유아 수학 문장제와의 상관관계
3) 유아의 연산능력과 수학 문장제와의 관계
유아의 연산능력과 유아 수학 문장제와의 관계를 알아보기 위해 Pearson의 적률상관분석을 실시 한 결과, 표 11과 같다. 유아의 연산능력은 수학 문장제 덧셈(
[<표 11>] 유아의 연령과 유아 수학 문장제와의 상관관계

유아의 연령과 유아 수학 문장제와의 상관관계
4) 유아의 수학 문장제 해결능력과 유아의 연령, 언어능력, 연산능력변인의 상대적 영향력
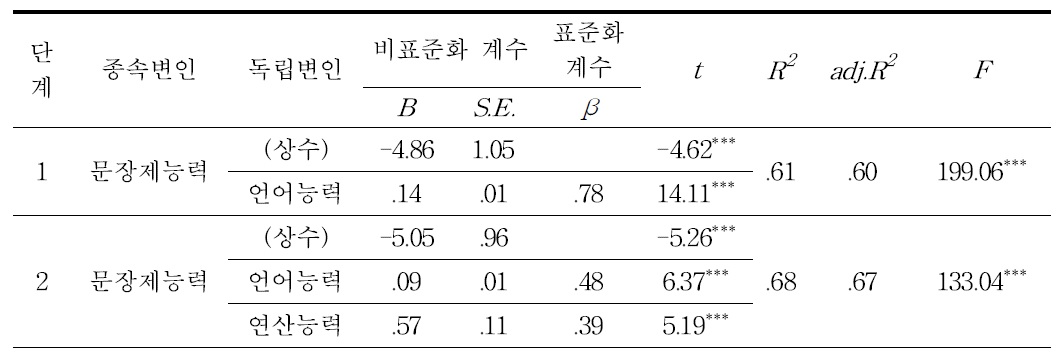
유아의 연령, 언어능력, 연산능력이 유아의 수학 문장제 해결능력에 미치는 상대적 영향력을 살펴보기 위하여 유아의 연령, 언어능력, 연산능력변인을 독립변인으로 유아 수학 문장제 해결능력을 종속변인으로 하여 단계적 다중회귀분석(multiple regression analysis)을 실시한 결과는 표 12와 같다. 연령은 중요변인으로 투입되지 않았으며 언어능력(
[<표 12>] 유아 수학 문장제 해결능력에 대한 연령, 언어능력, 연산능력의 다중회귀분석 결과
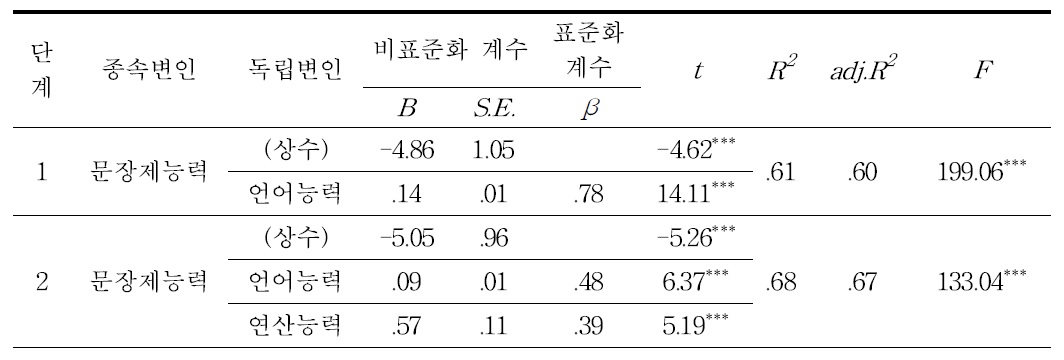
유아 수학 문장제 해결능력에 대한 연령, 언어능력, 연산능력의 다중회귀분석 결과
본 연구는 유아 수학 문장제 해결능력 검사도구를 개발하여 유아의 수학 문장제 해결 능력에 차이를 유발시키는 변인이 무엇인지를 파악 하고자 하는 연구이다. 이에 따라 초등학교 1학년 수학 교과서와 익힘책에 수록된 수학 문장제 문제를 의미론적 관점에서 분류하고 사용된 소재를 바탕으로 유아 수학 문장제 해결능력 검사도구를 개발하였다. 또한 유아 수학 문장제 해결능력과 연령, 언어능력, 연산능력 간의 관계와 그 상대적 영향력을 밝히고자 하였다. 본 연구의 결과를 중심으로 논의하면 다음과 같다.
유아의 수학 문장제 문제해결력 검사도구를 개발하기 위하여 초등학교 1학년 수학 교과서와 익힘책을 의미유형으로 분석한 결과 뺄셈의 감소유형 문항이 가장 많고, 덧셈의 합병유형, 덧셈의 증가유형, 뺄셈의 비교유형과 뺄셈의 덧셈 역연산유형, 혼합산, 덧셈의 뺄셈 역연산유형 순으로 나타났다. 이 결과는 이전 교육과정인 제7차 교육과정과 2007개정 교육과정의 2학년 교과서를 분석한 선행연구들(이대현, 2009; 이병옥, 안병곤 2008)과 맥을 같이한다. 이들의 연구와 본 연구의 결과를 종합해보면, 1학년 수학 교과서 문장제 문제의 계산별, 의미유형별 문항 비율이 2학년 교과서에도 그대로 이어지고 있음을 알 수 있다. 수학 문장제 문제 유형과 수학 문제 해결능력과 관련하여서, 국내 연구의 경우 변화유형, 결합유형, 동등유형, 비교유형 순으로 연산능력에 차이를 보이는 유아(홍혜경, 2009)와, 결합유형, 변화유형, 비교유형 순으로 수행에 차이를 보이는 초등학생들(김순혜, 송숙희, 김정원, 1998)의 연구가 보고되었다. 미국의 유치원 유아들의 경우에도 변화유형과 결합유형은 비교적 쉽게 해결하고 비교유형을 가장 어려워한다는 연구(Carpenter & Moser, 1984)가 보고된 바 있다. 이러한 연구 결과는 수학 문제 유형이 유아의 발달상 변화와 연령간의 관계를 고려하여 결정되어 짐을 짐작케 한다. 하지만 동일한 유형의 문제라도 문제 제시 방법이 달라질 경우, 문제 내의 언어 차이로 인하여 유아에게 매우 다른 의미로 전달될 수 있고, 이러한 의미 차이는 유아가 문제를 표상하고 해석하는 방법에 영향을 줄 수 있어 결국 문제해결 전략에도 영향을 미칠 수 있다. 한편, 문장제 유형별 사용 빈도와 관련하여서, 우리나라 학생들은 교과서에 높은 빈도로 포함된 문장제 유형에서 높은 문제 해결력을 보여준다는 연구(노현옥, 정은실, 2005)도 발표되었다. 이상의 연구 결과들을 고려해 볼 때, 유아교육계획안 구성 시 다양한 유형별 문장제를 제시하여 유아들이 여러 문장제 유형에 다각적으로 노출될 수 있도록 해야 할 것이다.
초등학교 1학년 수학 교과서와 익힘책의 수학 문장제에 사용된 소재는 실생활과 관련되어 있으나 매우 한정적인 소재가 반복적으로 사용되는 등 다소 제한적이었다. 수학 문장제 해결능력과 관련하여 소재는 실생활 관련성이 강조되며 이는 수학을 가르치는 목적 중 어떤 지식을 비슷한 상황에서의 경험을 기초로 하여 새로운 상황에 적용하는 능력인 교육적 전이와 관계가 있고 이는 두 상황의 동일성, 유사성이 많을수록 잘 일어나게 된다. 따라서 수학 문장제 문제에 사용되는 소재의 다양화를 통해 수학을 실생활에 적용하여 문제해결을 도모하는데 기여할 수 있다. 또한 유아들은 수학 문장제를 이용한 수학 문제의 해결의 경험을 통하여 수학을 실제 상황에 적용하는 응용력을 기를 수 있으며, 수학적 표현과 실제 상황을 관련시킴으로써 수학이 실생활에 적용 되는 것을 경험하게 된다. 이런 과정은 유아가 수학적 사고력과 창의력을 기르고, 실생활의 문제 해결에 수학을 이용할 수 있는 수학적 힘을 기를 수 있게 한다. 현재 유아교육현장에서는 생활주제와 관련하여 다양하고 광범위한 소재와 방법으로 수학 교육이 이루어지고 있다. 하지만 누리과정에 근거하여 흥미롭게 수학교육을 받은 유아들이 초등 수학 교과서의 단순 반복되고 한정적인 소재로 인해 수학의 흥미가 감소될 수 있다는 우려도 배제할 수 없다. 따라서 개정 초등 1학년 수학교과서의 문제점으로 지적되고 있는 수의 범위와 내용의 수준과 더불어 소재의 다양성도 향후 교과서 개발 시 고려되어야 할 것이다.
초등 1학년 수학교과서와 익힘책 내용 분석을 바탕으로 개발한 유아수학 문장제 문제 해결력 검사도구의 문항양호도를 알아본 결과, 문항통과율은 16.8∼77.4%로 이는 검사도구가 난이도별 문항을 골고루 포함하고 있음을 보여준다. 문항변별도는 모든 문항에서 상집단의 평균이 하집단의 평균보다 높았으며, 집단 간 평균의 차이가 통계적으로 유의미한 것으로 나타났는데, 이는 검사도구의 문항들이 유아의 문장제 문제해결력을 잘 변별할 수 있음을 시사한다. 내용단일성과 관련하여서도 각 문항 점수와 총점과의 상관이 .33에서 .69 사이로 비교적 높게 나타나 검사도구의 내용단일성이 신뢰할 만한 수준으로 검증되었다. 유아 수학 문장제 문제해결력 검사도구의 검사양호도를 알아본 결과, 문항 내적합치도 지수인 Cronbach
이상의 결과에도 불구하고 본 검사도구는 나름의 한계점을 가진다. 우선, 본 연구에서 개발된 유아 수학 문장제 문제해결력 검사도구는 누리과정의 수학교육과 초등학교 1학년 수학교육간의 연계성을 고려하여 초등학교 1학년 수학 교과서와 익힘책의 분석을 근거로 하여 개발하였으나 유아들의 인지발달 수준에 대한 상세한 분석을 바탕으로 하지는 않았다는 한계가 있다. 기존 도구들에 대한 분석이 포함되지 않았다는 점 또한 본 검사도구의 한계점으로 볼 수 있다. 현재 유아교육현장에서 정규 교과서가 사용되지는 않지만, 실제적으로 교사들은 교사용지도서를 많이 활용하고 있는 실정이다. 이를 고려하여 추후 연구에서 교사용지도서에 대한 분석이 이루어진다면, 좀 더 심도 있는 연구 결과를 기대할 수 있을 것이다.
2. 유아 수학 문장제와 연령, 언어능력, 수학능력간의 관계와 영향력
유아의 연령과 유아 수학 문장제와의 관계를 알아보기 위해 Pearson의 적률상관분석을 실시한 결과, 유아의 연령은 수학 문장제 덧셈, 문장제 뺄셈, 문장제 총점과 유의한 정적 상관이 있는 것으로 나타났으며, 그 중 문장제 덧셈과 가장 높은 상관이 있는 것으로 나타났다. 이 결과는 연령별 연산능력의 차이를 보고한 연구들(김소연, 2012; 최혜진, 이은혜, 2005)과 유아 수학 문장제 해결력은 연령이 증가함에 따라 증가한다고 보고한 연구결과(송연숙, 2002; 홍혜경, 2009)를 지지한다. 유아들은 일상생활 속에서 의미 있는 수학적 경험을 통해 다양한 더하기와 빼기 상황을 접하게 되고 이와 동시에 유아교육기관에서 교육을 받으면서 문제 해결능력도 발달시켜 나가게 된다. 또한 유치원이나 취학 전 교육에서 뺄셈보다는 덧셈을 먼저 학습하고, 실생활 상황에서도 뺄셈보다 덧셈을 경험하는 경우가 많아 이로 인하여 유아들은 뺄셈보다는 덧셈을 능숙하게 계산할 수 있다. 이렇게 볼 때, 유아의 연령과 수학 문장제 덧셈이 가장 높은 상관관계가 나타났다는 본 연구의 결과는 덧셈과 뺄셈에 대한 유아의 경험 차이에서 비롯된 것으로 판단된다.
유아의 언어능력과 유아 수학 문장제와의 관계를 알아보기 위해 Pearson의 적률상관분석을 실시한 결과, 유아의 언어능력은 수학 문장제 덧셈, 문장제 뺄셈, 문장제 총점과 유의한 정적상관이 있는 것으로 나타났다. 이 결과는 수학 문제해결능력과 언어능력의 상관관계에 관한 연구들(김은희, 2001; 이소영, 2008)과 일치하는 결과이며, 문장제 해결에서의 오류 발생률이 문제 이해과정에서 가장 높게 나타난다는 이병옥, 안병곤(2008)의 연구 결과와도 맥을 같이한다. 일상적인 상황의 맥락을 포함하는 수학 문장제 문제에서 언어는 문제를 이해하고 표상하는데 핵심적인 역할을 하며 문제의 표상은 제시된 문장에 대한 이해에서부터 시작된다. 즉, 언어적 능력이 높은 유아는 수학 문장제 문제를 정확히 이해하여 성공적으로 해결할 가능성이 높다는 것이다. 따라서 수학 문장제 문제의 해결력을 높이기 위해서는 언어능력을 향상시켜야 한다. 언어능력을 향상시키기 위한 방법에는 동화를 활용한 활동을 제안할 수 있다. 유아가 친근하게 접할 수 있는 동화를 반복적으로 들려주고 수학적 요소를 찾아내는 활동과 유아로 하여금 다시 이야기하거나 읽어보도록 하는 활동은 기존 유아교육현장에 적용이 용이하며 수학능력뿐 아니라 언어적 능력도 향상시키는 교육적 효과가 있을 것이다.
유아의 연산능력과 유아 수학 문장제와의 관계를 알아보기 위해 Pearson의 적률상관분석을 실시 한 결과, 연산능력은 수학 문장제 덧셈, 문장제 뺄셈, 문장제 총점과 유의한 정적상관이 있는 것으로 나타났다. 이 결과는 수세기 지식이 많을수록 수학 문장제 해결능력에서 더 높은 수행 점수가 나타났다고 보고한 연구(송연숙, 황해익, 2000)의 결과와 유사하다. 수학 문장제는 수학적 요소와 언어적 요소가 모두 포함되어 있으므로 올바르게 문제를 해석하였다 하더라도 계산능력이 부족하면 문장제 문제를 성공적으로 해결 할 수가 없다. 따라서 수세기 지식과 연산에 대한 기본적인 이해 및 사전 경험은 문제해결의 기반을 제공하고, 유아로 하여금 계산과정에서 문제를 해결하기 위한 다양한 문제해결 전략을 사용하도록 함으로써 성공적으로 수학 문장제 문제를 해결하게 하는 밑받침이 된다. 따라서 수와 연산능력이 높을수록 수학 문장제 해결 능력도 높음을 알 수 있다.
유아의 연령, 언어능력, 연산능력이 유아의 수학 문장제 해결능력에 미치는 상대적 영향력은 언어능력이 61%로 가장 많은 영향력을 나타냈으며, 연산능력 첨가됨으로써 7% 증가하여 68%를 설명하는 것으로 나타났다. 이 결과는 언어적 요인이 수학 문장제 해결에 더 영향을 미친다고 보고한 연구들(김미진, 1993; Mayer, 1983)과 맥을 같이 하는 것이다. 그러나 연산과정이 수학 문장제 문제해결에 더 영향을 미친다는 연구들(송연숙, 2002; 유승구, 1989)과는 차이를 보이고 있다. 유아의 문장제 문제해결에 있어, 유아의 연산능력의 영향력이 상대적으로 적게 나타난 것은 유아교육기관이나 가정에서 학습지 문제 풀이와 유사한 단순 계산만을 요구하는 덧셈, 뺄셈 교육에 더 치중하고 있어 유아들 간에 연산능력의 차이가 크지 않았기 때문인 것으로 여겨진다. 반면에 문장제 문제에 포함된 언어적 단서, 비교 관계에 대한 이해, 동사 결과나 시제에 대한 이해 등과 같은 문제 해독과정과 관련된 유아의 언어적인 능력은 유아마다 차이가 클 수 있으며, 이러한 차이로 인하여 유아 수학 문장제 문제 해결능력에 있어 유아의 언어능력이 높은 영향력을 보인 것으로 추측된다. 영향력에서의 차이는 있지만, 언어능력과 연산능력은 수학 문장제 해결에 함께 수반되어져야 하는 인지과제임은 분명하다. 따라서 향후에도 이들 변인간의 관계를 입증할 수 있는 후속 연구가 지속적으로 이루어 져야 할 것이다.