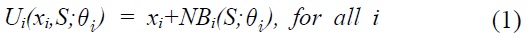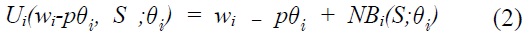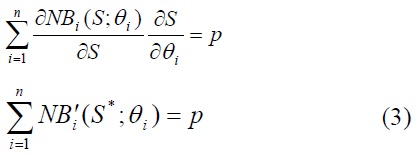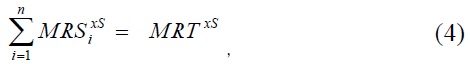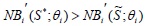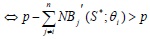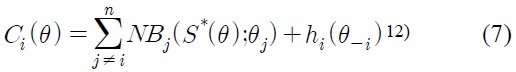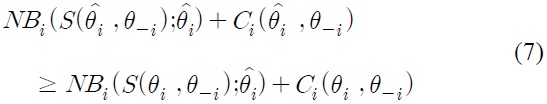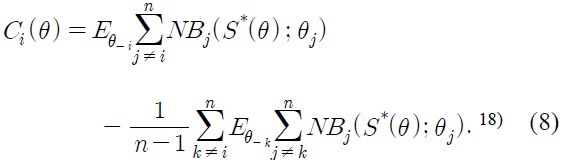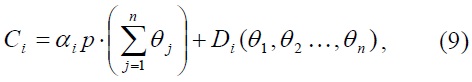IT security is becoming one of the most important IT requirements as more companies embrace electronic commerce as their core business strategy. Companies must establish information systems that provide secure access to trading partners and customers, and, at the same time, prevent malicious access by hackers, malcontents, and other intruders. Successful implementation of IT security is becoming a key infrastructure for successful electronic commerce, which creates an enormous business value by attracting and keeping customers. Consequently, IT security is becoming a top priority within firms to bolster and reinforce their forays into electronic commerce. More companies employ a more business-oriented approach, where the development of security policies and the implementation of efforts are viewed as an investment that makes economic sense by yielding positive returns in the future. A wide assortment of tools available companies can choose from facilitates this sophisticated approach. In fact, according to a survey, companies are planning to spend half their tech budgets on electronic commerce (Stepanek, 1999), and spending on IT security is believed to comprise a big portion of electronic commerce related investment.2) Given this increasing level of investment on IT security, economic consideration is a crucial part in the decision process of IT security-related investment.

However, there exist few economic analysis that provide useful guidelines for making critical decisions, such as the optimal level of provision of IT security and how to share the costs among different users within a firm. The main objective of this paper lies at examining economic features of IT security investment and comparing alternative mechanisms to achieve optimal provision of IT security resources within a firm.

The paper is organized as follows. In Section 2, we discuss the economic characteristics of IT security resource, followed by a discussion of previous research in Section 3. Section 4 provides theoretical framework for the analysis, and discusses the optimal provision condition with symmetric information and its interpretations. Also, Nash-Cournot equilibrium is discussed along with its problems in terms of optimality. Section 5 examines and compares three alternative mechanisms: i) the Clarke-Groves mechanism, ii) expected utility maximizing mechanisms, and iii) the Groves-Ledyard type mechanism. We also discuss strengths/weaknesses and applicability of each mechanism. The last section provides a brief summary of the results, and discusses limitations and further research.

2)According to a survey of 300 IT executives by Information Week Research, 84% of survey respondents said network security technologies, products, and services are on their project lists for 1999, beating year 2000 conversion and testing, Web server software, data ware-housing and mining, electronic commerce software, enterprise resource planning applications, and other strategic areas (Violino and Larson, 1999)

In this section, we discuss the economic characteristics of IT security provision problem, and briefly summarize previous research.

IT security resources share some unique characteristics. In particular, most IT security resources have externalities in two ways: nonrivalry of consumption and nonexcludability of benefit. The economic definitions of these two properties are as follows. First, a good is nonrival when the consumption of the good by one individual doesn't distract the consumption opportunity of the same unit to others. A classic example of nonrival goods is sunset. Sunsets are nonrival because one individual's consumption of sunsets doesn't affect the consumption of others when views are not obstructed. Some other examples include strategic nuclear weapons, weather monitoring stations, crisis-warning monitors, etc. Second, a good is nonexcludable when benefits of the good are available to all, or it is costly to prevent others from consume it once the good is provided. Some common examples include street lighting, fireworks, strategic weapons, pollution-control devices, radio broadcasting, etc. All these goods yield nonexcludable benefits because it is difficult or costly to exclude individuals form their benefits. In economics, goods that have these two characteristics are called purely public goods. On the other hand, private goods are fully rival and excludable. These two types of goods consist of the far ends of the spectrum of goods.

Nonrivalry of IT security resources is reflected in the fact that the total available IT security resources, once deployed, can be made available to each user within a firm. A single user's consumption doesn't affect the quantity available to other users. In addition, one user's deployment of IT security measures causes positive (and/or negative) benefits to other users within the same firm. Also, many IT security resources are nonexcludable because once they are deployed within the system it is costly to exclude some users from consumption, or, rather, it is preferable to include all users to maximize the level of security within the system. IT security can be defined as the protection of computing systems against threats to confidentiality, integrity, or availability(Summers, 1997, ch 1). IT security resources create a perimeter defense around the system within a firm. That is, IT security resources provide the same level of security to every user in the system. In fact, two most commonly used security technologies are password authentication and firewalls (Ernst & Young, 1999). These two technologies provide the same level of security to all users within the firm, and, therefore, nonrivalry and nonexcluable.

One other characteristic of IT security provision problem is information asymmetry. This is a recurring theme in economics, and many economic problems share this characteristic. The optimal provision of IT security resources problem is no exception. There exists some private information with regard to the valuation of an individual user for IT security goods, and, more importantly, an individual user has no incentive to reveal his true valuation unless truthful revealing is to his advantage.

Whang (1990) investigates alternative resource allocation mechanisms for congestion-prone computer resources. Also, Nadiminti (2002) examines the intrafirm resource allocation problem with asymmetric information and negative externalities, and proposes a mechanism that leads to optimal allocation. They incorporate externalities and information asymmetry in their analyses; however, the characteristics of nonrivalry and nonexcludability, which are unique to IT security resources as mentioned above, are not considered in their model.

In economics, since Samuelson (1954, 1955) first formally developed the theoretical framework for public goods, a vast array of researches has been conducted to examine and explain the economic nature of public goods. In particular, there has been extensive analysis of alternative allocative mechanisms, such as the Clarke-Groves demand-revealing mechanism (Clarke, 1971; Groves and Loeb, 1975), the Groves-Ledyard scheme (Groves and Ledyard, 1977) and a Bayes-Nash demand-revealing mechanism (Arrow, 1979) among others. These mechanisms have been extended and analyzed later in different settings. However, most of them are discussed within the pure public good framework. A main objective of this paper is to examine these mechanisms within the IT security provision setting.

In this section, we provide the analytical model for IT security provision within a firm. Based on this model, we derive the conditions for efficient provision at the overall firm level under information symmetry, and provide its interpretations. Also, we identify the problems with achieving the conditions in the real world, which mainly arise due to user behavior in the presence of conflict interest, and discuss the suboptimality of individual provision of IT security resources within a firm.

We consider an information system with n user departments indexed by i = 1, 2, …, n. Each user's preferences are defined over two commodities. The first is an ordinary private good whose quantities are denoted by x. The second is an IT security good, of which the user is able to consume the total available quantity, , where θ_i is the incremental amount of the security good proposed by user i and belongs to an open interval Θ_i in R. Here, θ_i identifies user i's tastes ("types") for the IT security good. The utility function of user i, U_i(x_i,S;θ_i), is assumed quasi-linear, and is written:

where NB_i3) denotes the net benefit of user i with type θ_i at the total available IT security good S. NB_i is continuous, strictly increasing, concave and everywhere twice differentiable. We assume that for any θ∈Θ, there exists S^*, which maximizes the overall value of the system.

With regard to the information structure, we assume that all the sets Θ_iare common knowledge, but the true value of the parameter θ_i is private knowledge. Also, NB_i is assumed to be common knowledge. Therefore, user i's utility function is fully known only when is known.

Note that equation (1) incorporates the characteristics of the economic characteristics of IT security goods discussed in the previous section. Nonrivaly is reflected in the fact that the total available quantity, S, is made available to each user. Also, nonexcludability is captured in the fact that regardless of each user's type, each user is not denied consumption of the units provided by other members of the system. In addition, the fact that θ_i is private knowledge reflects information asymmetry.

Maximization of utility is subject to constraints. For simplicity, we assume a linear trade-off between x and θ, and use the private good x_i as the numeraire in the analysis: x_i+pθ_i=w_i, where p is the unit price for the IT security good, and wi is the initial endowment of user i and common knowledge. Incorporating the budget constraint into the utility function, we can write (1) as follows:

An individual user i is assumed to be self-interested and make decisions to maximize his own valuation measure. In addition, the overall value of the system is defined as the aggregation of the utility of all the users in the system:

The efficient provision condition at the overall firm level can be found by maximizing the overall value of the system, which is defined as the aggregation of the utility of all the users in the system.

The first-order conditions for θ_i can be written as:

Thus, provision of an IT security good should be taken up to the point at which the sum of marginal net benefit of individual users equals the marginal cost of an IT security good. The intuition of this condition is that the marginal cost in terms of the amount of private good sacrificed should be equal to the marginal valuations of all users since the benefits of the IT security good are nonexclusively available to all users within the firm.

This result is one special case of the well-known Samuleson first-order conditions for a Pareto-optimal allocation of a pure public good. In a more general form, the Samuleson condition can be written as:

The optimal rule for the provision of a public good is, therefore, to allocate the resource such that the sum of the marginal willingness-to-pay (MRS4)) equals the marginal cost of provision (MRT5)).

Note that the differences between equation (3) and (4) are due to the assumptions made in this model. First, the marginal cost of provision is p since we use the private good x_i as the numeraire in the analysis. Second, the efficient level of S doesn't depend on the marginal utility of the private consumption x_i, thus only on the marginal utility of the security good, since we assume that the utility function has a quasi-linear form.

This condition shows the unique characteristics that should be considered in the resource allocation decision-making process with regard to an IT security good. These unique characteristics become clear when we compare this with the corresponding efficiency condition for private goods:

This difference, combined with information constraint and the user behavior, is the major source of practical problems in achieving an efficient provision of an IT security good within a firm. First, in the case of an IT security good, the efficiency condition (4) can be satisfied only when all the information regarding preference and utility of each user is available to everybody. However, in reality, this is often not the case. As it is assumed in this analysis, an individual user's preference on the level of the security good and its net benefit are private knowledge in the real world. There is no guarantee that a self-interested individual user will reveal his private knowledge to others unless it is maximizing his utility to do so.

Second, even when all information is common knowledge, the individual provision of an IT security good doesn't necessarily satisfy the efficient condition (4). In the case of private goods, equation (5) implies that a Pareto optimum can be achieved through an individual user's utility-maximizing behavior because individual users rely only on their own marginal valuation and don't have to include the marginal valuation of the rest of the firm when deciding their own efficient provision of an IT security good. However, in the case of the IT security good, the efficient condition (4) requires that the marginal valuation of all users should be taken into account, which will not necessarily be satisfied when individual users pursue utility maximization independently. This indicates that a collective or centralized effort is required to achieve the overall efficient provision of an IT security good within a firm. This problem will be further discussed in the next subsection.

This paper is motivated by the identification of these problems, which are embedded in the real world decision-making process for the provision of an IT security good within a firm. In particular, the main objective of this paper lies at investigating alternative demand-revealing mechanisms that induce a collective provision of an IT security good within a firm to be an efficient resource allocation under information asymmetry.

In the previous subsection, it is pointed out that the efficient provision condition at the overall firm level is not necessarily satisfied by individual utility maximizing behavior. In general, the tendency for public goods to be provided at suboptimal levels is a well-celebrated result in public economics. This problem is mainly due to the nonexcludability property of pure public goods. That is, individual users tend to under-contribute to provision in the situation in which they can rely on the contribution of others. This problem is also known as a free-riding problem. Proposition 2 examines this problem in the context of IT security good provision in this model, and shows that an individual provision results in a suboptimal solution, especially an under-provision of the IT security good.

where

The first-order condition for q_i can be written as:

where

Hence,

Next, we compare this with the efficient provision condition (3) to show that the level of provision in the Nash-Cournot equilibrium is less than the efficient provision at the overall firm level. Suppose, on the contrary, S^* < . Then,

Equation (6) clarifies the source of suboptimality of the Nash-Cournot outcome. Deciding the incremental amount of the security good, an individual user will make his best response only up to the level at which his own marginal rate of transformation, p, equals his marginal rates of substitution without taking into account of the other users' marginal valuations.

This result provides an economic rationale for the collective effort to be the optimal way of providing the IT security good within a firm. In practice, there could be other reasons to employ collective efforts, such as standard issues, streamlined implementation of security policies, ease of control, technical deficiency of user departments, etc. Along with these practical advantages for a successful implementation of the IT security good, the economic optimality also justifies the use of a collective approach for the provision of the IT security good within a firm.

3)NBi can be written as: Bi(S;θi) － Ii(S;θi). Bi(S;θi) is the benefit derived by the individual user i at the security good S. Ii(S;θi) is the cost other than each user's monetary contribution to the provision of IT security good S. Some of examples of this cost are decreased level of usability, extra efforts required or specific activities prohibited under the related policies for the proper operation of IT security measures. This 'indirect' cost may play a very important role in constructing an optimal incentive mechanism with which the overall benefit of IT security good could be maximized. Self-interested individual users may try to reduce the cost by violating the required rules; thus it can be denoted as Ci(S;θi, ai), where ai is action by user i. Often times, this action is not observable, resulting in a morale hazard problem. Since this paper doesn't include this problem in its analysis, we perform our analysis just with the net benefit in the model.  4)MRS is the marginal rate of substitution between two goods, and corresponds to the slope of the indifference curve.  5)MRT is the marginal rate of transformation between two goods, and corresponds to the slope of the production possibility frontier.  6)Since we are investigating outcome of individual utility maximizing behavior under information symmetry, it is reasonable to employ Nash equilibrium concept. Here, it is especially called 'Nash-Cournot' outcome because each user chooses his best response taking the quantity contributed by others as given.  7)Again, NBi is strictly increasing. Therefore, >0, for all i

In this section, we examine and compare three alternative demand-revealing mechanisms within the IT security resource provision context. We start this section with a discussion about the general structure of alternative demand-revealing mechanisms. And then, we discuss about each mechanism for its characteristics, practical implications and limitations.

To implement collective provision, we need to discover private information, known only by individual users. However, it may not be in the interest of users to reveal this information unless there exist proper incentives to do so. As utility-maximizers, users are motivated to manipulate the decision-making process to their best advantages by distorting their private information (the true incremental amount of IT security good, , in this model). Consequently, a fundamental problem of collective decision-making is to design mechanisms that both induce the revelation of the true information and choose an 'optimal' level of the IT security good within this framework of information asymmetry.

Alternative mechanisms are developed within the game theoretic framework under several alternative equilibrium concepts. The game among users and the central office8) is structured with the following three stages. First, the central office announces the resource allocation rule, which comprises of two functions: C(θ) and S(θ), where θ = (θ₁,θ₂, … ,θ_n). The charging function9), C(θ)=[C₁(θ), C₂(θ), … , C_n(θ)] decides how much each user is supposed to pay for the provision of the IT security good. S(θ) is defined to be in this model10), and decides the amount of the IT security good to be provided. Second, faced with the resource allocation rule, every user is supposed to send a message θ_i to the central office. Finally, receiving the message, the central office decides the charges for each user and the amount of the IT security good to be provided based on the C(θ) and S(θ) announced earlier.

For the analysis, the utility function of a user i for a mechanism (S(‧), C(‧))is written as

since the endowments of the initial wealth and the private goods play no role.

The mechanisms are developed employing several alternative equilibrium concepts: (non-Nash) dominant strategy equilibrium, the expected utility equilibrium, and the Nash equilibrium. In the following sections, we will examine the alternative mechanisms based on these equilibrium concepts within the IT security good context.

The Clarke-Groves mechanism is a celebrated proposal to induce users to make truthful revelation of valuation as their dominant strategies. The dominant strategy equilibrium concept is the strongest and most attractive notion because, under this equilibrium concept, truthful reporting of valuation is a dominant strategy for every user regardless of the reports submitted by others.

Following Vickery's (1961) discussion of a dominant strategy mechanism for inducing truthful reporting of valuation, Clarke (1971) and Groves (1973) present classes of dominant strategy mechanisms.11) These studies have been followed by a number of papers in the public good context (e.g. Tideman and Tullock, 1976; Green and Laffont; 1977) and congestion-prone computer resources (e.g. Whang, 1990), investigating properties and applicability of dominant strategy mechanisms. Laffont and Maskin (1980), in particular, showed how a number of questions about dominant strategy mechanisms in models with public goods can be conveniently formulated as systems of partial differential equations, and provided a description of charging functions for the dominant strategy mechanisms. Under the current setting, the charging function is given by

where S^*(θ) maximizes for any θ∈Θ, and h_i(θ_-i) is an arbitrary function of θ_-i = (θ₁,...,θ_i-1,θ_i+1,...,θ_n). The first term of the charging function, the sum of the net benefits of other users, provides the individual user the incentive to report truthful parameter. The second term, an arbitrary function of reported valuations of others, preserves incentive compatibility and allows the central office the freedom to ensure that the total charge will at least cover the cost of provision.

This charging scheme is well known to induce the users to make a truthful reporting as a dominant strategy no matter what other users do.

Proposition 3: Under the charging scheme C, truthful revelation of is a dominant strategy for user i, for any θ_-i.

By definition, the truth is a dominant strategy for the mechanism if, for any i and any θ∈Θ

for which S(θ) maximizes . Now, incorporating the charging function C_i(θ) to equation (7), we can rewrite equation (7) as

From the definition of S^*(θ), C_i(θ) satisfies this inequality, and, therefore, θ_i = is a dominant strategy for user i.

The notable property of this mechanism stems from its underlying equilibrium concept. Under this mechanism, revealing truthful information is a best strategy for each user regardless of other users' behavior.

This property is the source of two attractive features of this mechanism. First, it doesn't require any knowledge of other users' truthful valuation when a user considers his strategy. This is especially attractive in a situation where each user is asked to report his preference parameter, while knowing nothing about the other users' valuation of the IT security good. In fact, as it is assumed in the model of this paper, this situation is the most probable case in reality. Second, under dominant strategy equilibrium, if it exists, we can certainly expect that it will be adopted.13) Therefore, there exists no coordination problem. These attractive features make the Clarke-Groves mechanism to be a very simple and applicable resource allocation tool in practice. Also, it is the most preferable mechanism when there is no information available, or it is very costly to share the necessary information among users.

However, this mechanism is not immune to shortcomings. The most significant weakness is that the Clarke-Groves scheme mechanism leads in general to the budgetary problem of balancing the transfers.14),15)

This is a well known deficiency of the Clarke-Groves mechanism as it is studied and discussed in several literatures (e.g. Groves and Ledyard, 1977b; Cornes and Sandler, 1996, ch.7). This problem is mainly due to the underlying equilibrium concept, the dominant strategy equilibrium, which imposes rather strong incentives to truthful reporting.

This budgetary problem results in the lack of full employment of resources, and accordingly, may hurt the overall outcome of the firm in the general equilibrium sense due to the opportunity cost incurred from the budget surplus. That is, consumption of the IT security good may be optimal, but consumption of other goods is low. In particular, this problem is critical to profit-maximizing firms, for whom the efficient use of every available resource is critical.

One way to overcome this budgetary problem of the Clarke-Groves mechanism is to apply a less strong equilibrium concept. One line of research has applied the expected utility equilibrium, pioneered by Harasanyi, to design the incentive compatible mechanisms that achieve the budget balance. In particular, d'Aspremont and Gerard-Varet (1979), among others, has shown that if a compatibility condition is imposed on the individual beliefs and if a Bayesian solution16) is given to the incentive problem, then it is possible to avoid the budgetary problem. Also, Laffont and Maskin (1979) has extended the differential approach of above cited studies, and characterized the family of individually incentive compatible expected utility maximizing mechanisms.

Under this equilibrium concept, a mechanism [S(·), C(·)] is said to be individually incentive compatible with respect to expected utility maximization if and only if, for any i and for any θ_i,

where f_i(θ_-i)17) is the probability density function reflecting user i's beliefs about the strategies, θ_-i, of the other users.

In our setting, we can consider the expected utility problem of choosing C(θ)=[C₁(θ), C₂(θ), … , C_n(θ)], such that and so that for all i and all ,

where S=S^*(θ) maximizes . Also, suppose that we restrict the charging functions to be additively separable, that is,

From equation (7) we get

Since d_ij(θ_j), j≠i are irrelevant for incentive compatibility, they can be chosen to balance the budget in the following simple symmetric way:

Deleting the constants (), we obtain

The first term of this charging function is the sum of the expected net benefit generated by other users. The second term is the average of the first term of every other user's charging function. As shown in the proof, this term achieves budget balance without influencing the user's choice of reported valuation because the term doesn't depend on the user's own reported valuation.

Cornes and Sandler (1996, ch.7) provides a good summary of the basic message of the expected utility maximizing mechanisms. If we think of the individual as drawn from a known probability distribution with respect to their valuations, then a set of transfers can be defined such that (i) a component of the transfer each receives will be the expected benefit to others implied by the recipient's reported valuation, (ii) net transfers will be zero, and (iii) truthful revelation of valuation will be the preferred strategy for each, given truthful revelation by others.

This mechanism has some strengths and weaknesses. The most significant strength of this mechanism is obviously its ability to achieve budget balance. Therefore, it can lead to an efficient allocation of resources at the overall firm level, which was generally unachievable under the dominant strategy mechanism. However, the underlying assumptions that induce this strength is also the source of the weaknesses of this mechanism. The budget balance is achieved with the two important changes of the assumptions with regard to information constraints and the equilibrium concept. First, each user needs to have statistical information about the valuation of others. In practice, there could be a situation in which having this knowledge is a remote possibility. Second, the Bayes-Nash equilibrium concept shares the fundamental problem of the Nash equilibrium: there may exist multiple equilibria, so that which strategy will each user actually choose is not clear.

Despite these weaknesses of the expected utility mechanism, in general, it is regarded to have the great attraction of handling the problem of incomplete information. The biggest obstacle for this mechanism to be applied in practice is the availability of necessary information. However, we can think of the situation in which a class of statistical information could be available on the basis of some preliminary surveys or previous empirical evidence. If this information could be agreed on by all users and can be imposed upon users' future reporting behavior,19) this mechanism can be nicely implemented in a real world situation.

One other possible equilibrium concept is Nash equilibrium. Groves and Ledyard (1977b) employs this concept and presents a set of quadratic tax functions that are individually incentive-compatible and balance the budget. Brock (1980) provides a systematic method of constructing Groves-Ledyard type mechanisms in different situations and for different objectives. In this section, we will present the model and results of this mechanism and discuss its implication for our IT security good context.

Under our basic model presented in 4.1, the Groves-Ledyard scheme tax function presented in Brock (1980) is given by

where α_i > 0, =1, and nontrivial D_i that satisfies =0, =0.20)

It is well known that this mechanism satisfies the efficiency condition and the budget balance condition. Also, faced with this tax function, for each individual user i, telling the truth is preferable if everyone else is doing so. That is, truthful revelation is a Nash strategy.

This mechanism has two notable features. First, notice that the tax function (9) doesn't depend on utility functions. Therefore, no knowledge on individual user's utility function is required. Remember that in the model in Section 3.1, Section 4.2 and Section 4.3, the analysis and the mechanism design is performed under the assumption that the function NB_i is common knowledge and the information asymmetry comes from the lack of information of θ_i. Therefore, this mechanism can be a very useful resource allocation mechanism tool for the IT security provision in a situation where no prior knowledge with regard to the net benefit function is available. Second, this tax function gives a good insight on the efficiency of the conventional cost allocation method: conventional cost allocation method is not an efficient cost allocation method when information about θ_i is common knowledge. We will discuss this in Proposition 5 below.

The Groves-Ledyard mechanism shares the same problems with the expected utility maximizing mechanisms to some extent. First, in terms of required information, even though the mechanism doesn't require knowledge on the net benefit function, we need information about θ_i as common knowledge. This could be a very strong21) requirement in some real-world situations. Second, it shares the problem of multiple equilibria since the underlying equilibrium concept is Nash equilibrium.

8)The central office is introduced in the game as the player who coordinates the collective decision-making process.  9)It is commonly called 'tax function,' or 'transfer function' in public economics literatures.  10)In fact, this is the capacity decision rule that maximize , given the assumptions on the net benefit function in this paper.  11)This is why the dominant strategy mechanisms are called as 'the Clarke-Grove scheme.'  12)The general form of the charging function has the following characteristic: where is an arbitrary function of θ-i The proof is similar to the one Laffont and Maskin (1979) and hence omitted here.  13)This will be further discussed later when we discuss about mechanisms based on the Nash equilibrium concept.  14)The budget is balanced in the sense that the amount allocated to the construction of each public good is equal to the amount spent on the construction of each public good under the tax function (Brock, p.46). In the setting of this analysis, given the utility function, NBi(S(θ);)+Ci(θ), the balance budget means   15)On the other hand, Green and Laffont (1979, ch. 9) examined a number of situations in which the absolute size of the surplus decreases, as the number of individuals gets larger, and argued that this problem may not be too serious. Also, Laffont and Maskin (1980) showed the budget balance can be achieved for rather extremely limited classes of utility functions, and presented a necessary and sufficient condition for an admissible family of valuation functions to admit a balanced satisfactory mechanism.  16)With this solution concept, this equilibrium concept is also commonly called 'Bayes-Nash equilibrium' concept, and, accordingly, the expected utility maximizing mechanisms are also called 'Bayes-Nash mechanisms.  17)Notice that fi(θ-i) doesn't depend on θi. That is, it requires that for every player i, fi(θ-i|θi)=fi(θ-i|)=fi(θ-i), for any θi, . This assumption is called the 'independence condition,' and is very restrictive in terms of information since it implies in fact that the true beliefs of any user is of common knowledge (d'Aspremont and Gerard-Varet, 1979).  18)  19)For example, the central office rejects any announcement outside this restricted class.  20)Brock (1980) also shows that the tax function presented in Groves-Ledyard (1977b) is an example that satisfies these conditions. Under our setting, the Groves-Ledyard tax function can be denoted   21)This is even stronger than just a statistical knowledge required for the expected utility maximizing mechanism.

This paper investigates the resource allocation problem with regard to IT security provision within a firm. The most notable contribution of this paper may be importing some analytical methods and studies in public economics to the context of IT security good provision within a firm. Major research outcomes can be summarized as follows. First, this paper discusses the efficient condition for the provision of IT security goods that have unique economic characteristics, namely, nonrivalry and nonexcludability under information symmetry, and provides an economic rationale for the optimality of a collective provision effort. Second, this paper examines alternative demand-revealing mechanisms under information asymmetry in the IT security provision context. Each mechanism has its strengths and weaknesses, and, accordingly, different applicability in practice. The Clarke-Grove mechanism may be the most attractive and easy-to-apply mechanism because it requires a minimal amount of information and its equilibrium outcome is unique (if it exists). However, it has a significant weakness of unbalanced budget, which leads to the lack of full employment of resources. The expected utility maximizing mechanism and the Groves-Ledyard mechanism solves this problem. However, it requires some extent of prior information regarding individual users' valuations, resulting in limited applicability in practice. However, it could selectively be used depending on the types of appropriate information available. This paper also shows that the traditional cost allocation method doesn't achieve an efficient resource allocation in a certain context.

As a preliminary study for this matter, the scope and rigor of analysis are somewhat limited, and this could open a door to future research. First, in the model, we don't incorporate uncertainty involved in the problem. In fact, uncertainty may play a crucial role in making important decisions on the IT security provision. For example, two firms with the same level of IT security resource can have a different level of possibility of being attacked due to some conceivable reason, such as a firm's just being a favorite target for hacking and the nature of the business of the firm. Also, rapid technological development makes the environment volatile. Users may make totally different choices under uncertain situations, and consequently, quite different mechanisms should be required to reach an optimal resource allocation of IT security goods within a firm.

Second, all the mechanisms discussed in the paper are based on noncooperative equilibrium concepts. However, a group of users might have an incentive to make a coalition to their advantages. The central office might need to have mechanisms with quite a different structure to cope with this cooperative behavior by users.

Third, as briefly mentioned previously, actions by individual users that comply with the IT security policy are very crucial to maximize the overall benefit of IT security investments. However, these actions are usually unobservable or very costly to verify. Therefore, we need not only to have demand-revealing mechanisms to induce truthful revelation of valuation, but also to construct optimal contract schemes to result in policy-complying actions by users.

Finally, all the analyses in this paper are conducted within the scope of a firm. However, the nature of the networked economy and the electronic commerce necessitates rapidly increasing level of interconnection with outside firms and customers. In fact, this changing nature of business environment leads to the growing importance of IT security for successful business of firms. All the same questions addressed in this paper could be asked to the context of inter-firm security provision environment. The implications, however, could be somewhat different.