Forming coherent mental representations of visual objects is an integral part of the visual system (Peissig & Tarr, 2007). Such representations involve both perceptual and cognitive processes and provide essential information for understanding our visual environments (Palmeri & Gau thier, 2004). Research on visual memory (Cooper & Schacter, 1992; Loftus, Miller, & Burns, 1978; Loftus & Palmer, 1974; Schacter & Cooper, 1993; Schacter et al., 1995; Squire, 1998), visual object classification (Mack, Gauthier, Sadr, & Palmeri, 2008), symmetry perception (Driver, Baylis, & Rafal, 1992; Yamauchi et al., 2006), and face recognition (Bukach, Gauthier, & Tarr, 2006; Gauthier & Bukach, 2007; McKone, Kanwisher, & Duchaine, 2006) are all linked to the central issues of object representation (Biederman & Bar, 1999; Biederman & Cooper, 1991, 1992; Marr, 1981; Marr & Nishihara, 1978; Peissig & Tarr, 2007; Poggio & Edelman, 1990; Tarr, 2003; Vuong & Tarr, 2004).
One technical problem blocking the progress of this line of research is the difficulty of developing realistic three-dimensional stimuli. A majority of visual perception and cognition studies have employed two-dimensional line drawings or simple pictures of three-dimensional objects as stimuli (Biederman & Bar, 1999; Biederman & Gerhardstein, 1993; Gauthier & Tarr, 1997b; Hayward & Tarr, 1997; Subramaniam, Biederman, & Madigan, 2000; but see Gauthier & Tarr, 1997a for some exceptions). The problem is that neurons in the visual cortex are highly interconnected, and, often times, these neurons respond differently in natural viewing conditions (Carandini et al., 2005, p. 10588; Felsen & Dan, 2005; Yuille & Kersten, 2006; Smyth, Willmore, Baker, Thompson, & Tolhurst, 2003; Touryan, Felsen, & Dan, 2005). In this regard, investigating behavioral responses to simple stimuli such as edges, blobs, bars, or line drawings may not give us the accurate picture of the visual system in question (Barlow, 2001; Felsen & Dan, 2005; Simoncelli & Olshausen, 2001).
This problem is particularly serious in symmetry perception research. Symmetries of objects are pivotal in both structural description models and view-based models of object representation. Research has shown that visual symmetries provide strong cues for image segmentation, such as distinguishing a figure from its background (Driver et al., 1992). The consensus is that symmetry perception occurs
However, these claims were limited by results based on simplified twodimensional stimuli (e.g., Baylis & Driver, 1994). Recently, although some progress was made in the field of symmetry perception with three-dimensional objects (e.g., Niimi & Yokosawa, 2009), most findings of symmetry perception have been performed with two-dimensional objects. To remedy this problem, we developed an archive of three-dimensional stimuli using 3D Studio Max (see Appendices A & B for stimulus archive and tutorial) and investigated the nature of symmetry perception with realistic threedimensional stimuli (see
1.1 Symmetry and object representation
In Biederman’s (Biederman, 1987; Hummel & Biederman, 1992) recognition-by-components theory, the visual system extracts two-dimensional edge properties such as curvature, co-linearity,
However, it is unknown whether the same process is involved in symmetry perception of realistic three-dimensional stimuli. Symmetry may emerge spontaneously without attention for simple two-dimensional stimuli (Driver et al., 1992 but see Olibers & Helm, 1998); yet, a more elaborate mechanism may be required for realistic three-dimensional objects. The construction of object structure by three-dimensional local components involves the binding of image features to objects, and this binding process is incomplete unless attention is given to the relevant locations (Logan, 1990; Treisman & Kanwisher, 1998; Stankiewicz, Hummel, & E. E. Cooper, 1998). This means that symmetry perception for three-dimensional objects can be an incremental process, where symmetry is extracted gradually as the global structure of objects is recovered. We tested this idea in two experiments.
In Experiment 1, we examined the accuracy and response times of participants judging the symmetry or asymmetry of individual stimuli, where the complexity of stimuli and the duration of stimulus presentation were manipulated. We varied the number of local components of individual stimuli and examined how the complexity of stimuli, as measured by the number of distinct components that each object had, interacted with the accuracy and speed of symmetry perception. As observed in two-dimensional stimuli, if symmetry perception occurs spontaneously in realistic three-dimensional stimuli, the accuracy and response times of symmetry perception should be relatively independent of the duration of stimulus presentation and the complexity of stimuli. Contrary to this view, the results of Experiment 1 show that symmetry perception for three-dimensional stimuli is highly reliant on the duration of stimulus presentation and the complexity of stimuli. In Experiment 2, we implemented an incidental recognition memory experiment and examined whether stimulus complexity, as defined in Experiment 1, would also influence recognition memory performance. The results of Experiment 2 show that the stimulus complexity influences recognition memory performance when the study task involves incidental encoding of the global structures of objects.
Experiment 1 examined the extent to which the presentation duration and the complexity of stimuli influence symmetry detection of threedimensional objects. The hypothesis that symmetry perception for threedimensional objects requires a gradual recovery of 3D structures predicts that presentation duration and stimulus complexity influence symmetry detection considerably. To test this prediction, participants judged the symmetry/asymmetry of stimuli in 5 different time durations (30, 40, 50, or 60 millisecond), as well as without time limitations. The complexity of stimuli was also manipulated by varying the number of distinct local components of which individual stimuli were composed.
2.1.1 Participants
All participants (
2.1.2 Stimuli and procedure
Sixty symmetric objects and 60 asymmetric objects (
The stimuli extended approximately 4.0 degrees of visual angle.2 The procedural details of stimulus generation are described in Appendices A and B; the tutorial is based on 3ds Max, release 10.
The task for participants was to indicate whether stimuli shown on the computer screen were symmetric or asymmetric by pressing designated keys. To start each trial, participants pressed the space bar, which generated a fixation cross, visible for 500 milliseconds. After the fixation cross disappeared, a stimulus was presented and remained at the center of the computer monitor until participants responded. To indicate the symmetry/asymmetry of the stimulus, participants pressed the left or right arrow key. Immediately after participants pressed one of the arrow keys, the monitor displayed a sign indicating a directive to press the space bar, which led to the presentation of the fixation cross and the next stimulus. The stimuli were presented by a Dell OptiPlex GX240 with Pentium IV processors (2.4 GHz) on a Gateway vx730 monitor with a resolution of 1280 x 1024 pixels.
2.1.3 Design
The experiment had a 5 (presentation duration; 30ms, 40ms, 50ms, 60ms, unlimited, between-subjects) x 2 (stimulus complexity; low, high) factorial design. The dependent measure was detection accuracy (d’) and response times.3 For the detection accuracy measure, we defined “hit” as responding “symmetry” given symmetric objects, and “false alarm” as responding “symmetry” given asymmetric objects (see Barlow & Reeves, 1979; Wenderoth, 1997 for a similar procedure). Calculated this way, this measure helps control possible response bias (Ratcliff & McKoon, 1995; Roediger & McDermott, 1994). Because detection accuracy differed drastically in each presentation duration condition, the response times were measured for all trials rather than just the trials with correct responses.
To assess the impact of stimulus complexity, we measured the number of distinct local components that each stimuli had. This measure yielded two stimulus complexity categories: low and high complexity. For asymmetric objects, low complexity objects had 1 or 2 distinct kinds of components and high complexity objects had 3 to 5 distinct components (low complexity objects,
There was also a reliable main effect of stimulus complexity;
Taken together, these results show that symmetry detection for threedimensional objects depends on the duration of stimulus presentation and the complexity of stimuli, suggesting that detection of symmetries of 3D objects is unlikely to be spontaneous and preattentative.
1The “primitive components” used in our stimuli are defined and produced strictly in the 3ds Max program, and “primitives” are different from geometric primitives/parts as defined and characterized by Biederman (1987) or by Hoffman and Richards (1984). 2All stimuli and data for individual objects can be downloaded from http://people.tamu.edu/~takashi-yamauchi/stimuli/ and http://people.tamu.edu/~takashiyamauchi/stimuli/data/ 3Hit and false alarm scores equal to 1 or 0 were converted to 0.99 and 0.01, respectively, in order to calculate Z-scores.
In Experiment 2, we investigated the relationship between symmetry perception and “stimulus complexity” indirectly in a recognition memory test. Previous studies investigating implicit memory of three-dimensional objects suggest that global structures of objects such as orientation axes of symmetry can be formed after an encoding task in which participants judged the left-right orientation of objects (Liu & Cooper, 2001; Yamauchi et al., 2006). This encoding task is also known to produce priming in symmetry/asymmetry judgments. Thus, if the stimulus complexity that is defined in Experiment 1 is psychologically real, it should affect the performance for the incidental recognition memory task. We tested this idea.
The experiment consisted of two phases: a study phase and a test phase. During the study phase, participants studied left-right orientations of 30 symmetric and 30 asymmetric objects. After the study phase they were given a recognition task in the test phase. This experiment was conducted incidentally in that participants were not aware of the intent of the experiment during the study phase (an incidental test). In an additional follow-up study, we also investigated the relationship between stimulus complexity and intentional recognition memory performance. The intent of this follow-up study is explained in the Result section.
3.1.1 Participants
A total of 60 undergraduate students (female = 40; male = 20) from Texas A & M University participated in Experiment 2 for course credit. All participants had normal or corrected-to-normal visual acuity.
3.1.2 Stimuli and procedure
The materials used in this experiment were identical to those described in Experiment 1. Of the total 60 symmetric objects and 60 asymmetric objects, 30 asymmetric objects and 30 symmetric objects were shown in the study phase, and all 120 (60 symmetric and 60 asymmetric objects) were shown in the test phase. We developed two versions of stimuli for counterbalancing.
In the study phase, 30 symmetric objects and 30 asymmetric objects were randomly presented one at a time at the centre of the screen for five seconds each. Participants examined each object as a whole for the entire 5 seconds and judged whether the object faced primarily to the right or to the left by pressing one of two specified keys (see Schacter et al., 1990, for this task). No mention was made at this point about the subsequent recognition task. Shortly after the study phase, participants proceeded to a recognition task, in which participants made ‘yes/no’ recognition responses for studied and non-studied objects.
3.1.3 Design
The main dependent measure was d’ calculated from hit and false alarm scores obtained in the recognition memory task. “Hit” is defined as the probability of responding “old” given that the stimulus appeared during the study phase (p(response = “old” | old)) and “false alarm” is defined as the probability of responding “old” given that the stimulus did not appear during the study phase (p(response = “old” | new). To analyze the relationship between stimulus complexity and recognition memory, an item-based linear regression analysis was applied to the data with the stimulus complexity measures (i.e., the number of distinct local components) as a predictor variable.
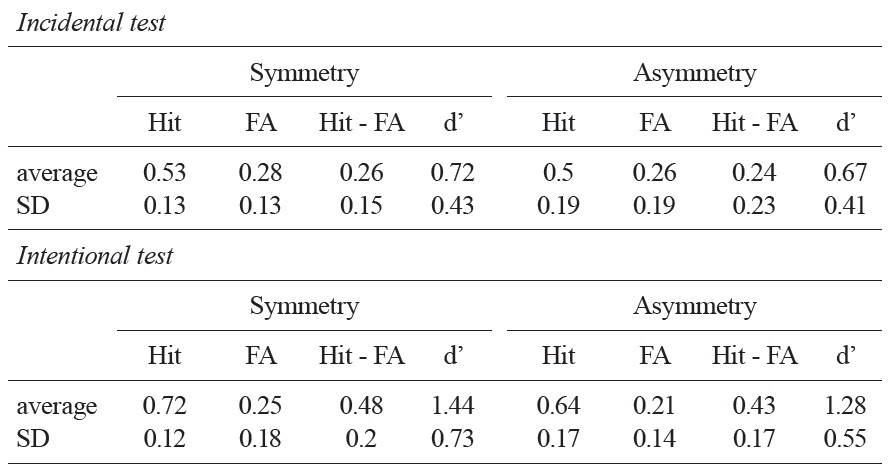
Table 1 summarizes the results from the recognition memory test. The average hit minus false alarm scores of asymmetric objects and symmetric objects were 0.24 and 0.26, respectively. In both cases, these scores were significantly higher than a chance level, indicating that participants were able to distinguish individual objects in their recognition memory; asymmetric objects,
As predicted, a linear regression analysis applied to individual objects revealed that there is a significant linear relationship between stimulus complexity and recognition memory performance when the study task was given incidentally;
[Table 1.] A summary of the recognition memory tests in Experiment 2
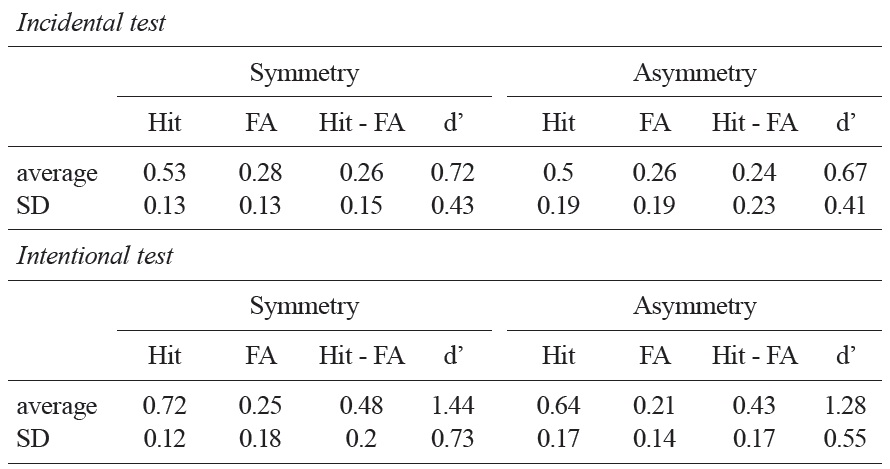
A summary of the recognition memory tests in Experiment 2
In a follow-up study (
4.1.1 Participants
A total of 30 undergraduate students from Texas A & M University participated in Experiment 3 for course credit. All participants had normal or corrected-to-normal visual acuity.
4.1.2 Stimuli and Procedure
The materials used in this experiment were identical to those described in Experiment 2. Participants in this follow-up study did not carry out the leftright orientation task for individual stimuli during the study phase; instead, participants actively studied stimuli for a subsequent memory task in any way they wanted. Studies showed that the intentional memory task leads people to form semantic associations of stimuli (Cooper, Schacter, Ballesteros, & Moore, 1992; Schacter et al., 1990; Schacter & Cooper, 1993). In this regard, it was expected that the stimulus complexity as measured by the number of distinct components would not relate to participants’ recognition performance in this case.
4.1.3 Design
The main dependent measure was the same as Experiment 2.
As expected, there was no statistically significant link between the stimulus complexity variable and the recognition memory performance in the intentional memory task;
The results from these two experiments indicate that there is a strong possibility that symmetry perception for three-dimensional objects is an incremental process, where symmetry is extracted gradually as the global structure of objects is recovered. In Experiment 1, we reasoned that if symmetry perception emerges gradually as global three-dimensional information is recovered from the image data then symmetry detection should be influenced by the complexity and presentation durations of stimuli. The results of Experiment 1 were consistent with this view. Experiment 2 employed an incidental memory task. In this setting, participants judged the left-right orientation of stimulus objects during the study phase and later tested their recognition memory of these objects in the test phase. As predicted, the results of Experiment 2 revealed that recognition memory performance was highly correlated with stimulus complexity when the study task involved incidental left-right orientation judgments, but not when the study task involved intentional encoding. Taken together, these results are consistent with the view that symmetry perception in three-dimensional objects emerges in an incremental process, where symmetry is extracted gradually as the global structure of objects is recovered.
5.1 Implications: Symmetry Perception and Object Representation
Clearly, at the very early stage of object representation, some form of part decomposition and the assignment of edges to a figure should occur. At this stage, some form of coarse descriptions of object parts occurs (e.g., Hoffman & Ridchards, 1984), and this coarse representation of object parts probably suffices for initial symmetry detection relevant to two-dimensional images. After this stage, symmetry perception for three-dimensional stimuli arises gradually as figure-ground segregation is achieved (see also Sekuler & Palmer, 1992; van Lier, Leeuwenberg, & Helm, 1997). We suggest that symmetry detection is likely to go through multiple-stages (Wagemans, 1997). Given the current finding that symmetry perception for three-dimensional stimuli depends on stimulus complexity and presentation durations, the later stages of symmetry perception may employ a constellation of features as cues determining the axis of symmetry, which can be identified, for example, by processing local energy functions (the intensity of pixels) and then local maxima of a convoluted image. This process proceeds iteratively as more fine-tuned features are recovered from the original images (e.g., Scognamillo, Rhodes, Morrone, & Burr, 2003).
In Biederman and Hummel’s model of object representation and recognition (Biederman, 1987; Hummel & Biederman, 1992; see also Marr, 1981; Marr & Nishihara, 1978), a limited number of geometric primitives and their configurations render the representation of a variety of basiclevel objects. The model suggests that constructing three-dimensional local components from two-dimensional non-accidental image data requires the detection and integration of different image features (Biederman, 1987). In order to combine these properties, some attentional mechanisms may be deployed. We suggest that symmetry perception for three-dimensional objects appear as these local three dimensional features are recovered gradually. Future research should investigate exactly how the recovery of threedimensional features eventually gives rise to the extraction of global axes of symmetry.