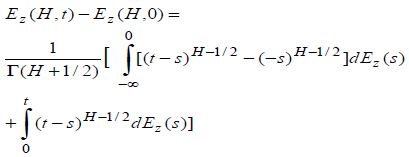The four great inventions: nautical compass, gunpowder, papermaking and printing have been famous for their historical significance in Chinese culture and can be regarded as important contributions to human civilization by the ancient Chinese (Needham, 1954; Needham, 1969). As a matter of fact, there were other Chinese inventions that were more sophisticated and even had greater impact on world civilization, such as traditional Chinese medicine (TCM) and its lunisolar calendars, etc (Lu and Needham, 1980; Needham, 1959; Needham et al., 2000). However, due to lack of historical knowledge, self-confidence and scientific insight, many prominent and leading Chinese scholars such as H. J. Ren, Q. C. Liang and Y. L. Feng started writing papers as early as 1915 to investigate on the reasons why “China has never had anything that can be called science.” It is very sad and disturbing because these erroneous viewpoints will have bad influence on our descendents and eventually will destroy and wipe out some of the most precious legacy of human beings. Unfortunately, there is no lack of such kind of scholars even nowadays in modern China.

On the other side of the world, however, a renowned English biochemist and historian of Chinese science and technology called Joseph Needham, thought differently. For more than 30 years, his work on the history of Chinese science and technology had elucidated the achievements and developments of the science, technology, and medicine indigenous to the East Asian cultural area. Hence, in the schematic diagram of his book, he used the levels of scientific achievement versus time to show the roles of Europe and China in the development of ecumenical sciences (Needham, 1970). In that diagram, Needham showed the curves of level of scientific achievements of China and Europe since the 3^rd century B.C. all the way up to the 20^th century A.D. The curve was a slowly increasing linear function of time for China. Yet, that curve of Europe was a convex function of time with an abrupt surge only in the recent three centuries. He then continued to point out two kinds of important points in that diagram for several scientific disciplines: (1) transcurrent and (2) fusion. The first kind of “transcurrent point” designated the moment at which the European scientific and technical level surpassed that of China. The second “fusion point” designated the moment at which the body of knowledge and technique of China was successfully incorporated into the modern system. According to him, the two kinds of points for astronomy were around the years of 1,610 and 1,640, for physics were around 1,700 and 1,880, and for botany around 1,780 and 1,880, respectively. Interestingly enough, according to Needham, medicine had only the transcurrent point around 1,800, but no fusion point yet (Needham, 1970). This fact implies that TCM is still alive and vibrant nowadays without being incorporated into the modern Western medical system.

It was then proper and fitting for him to ask the following important “Needham’s Grand Question” (NGQ) which basically contained two parts (Needham, 1969). (1) Why did modern science take its meteoric rise only in the West at the time of Galileo? (2) Why was it that between the 2^nd century B.C. and the 16^th century A.D., East Asian culture was much more efficient than the European West in applying human knowledge of Nature to useful purposes? Here, the definition of modern science which took place in the West, according to Joseph Needham, has to be clearly defined first. By this, he meant, “the testing by systematic experiment of mathematical hypotheses about natural phenomena” that was originated only in the West. From his viewpoint, this “new or experimental philosophy of the West” ineluctably overtook the levels reached by the traditional Chinese natural philosophy (TCNP), “leading in due course to the exponential rise of modern science” in the 19th and 20th centuries (Needham, 1969). Some of the successful examples, according to him, were as follows. Galileo (1564 - 1642) proposed the theory that planetary orbits were circles. Kepler (1571 - 1630) improved the theory of planetary orbits to ellipses with his three laws. Then, Newton (1642 - 1727) proposed his three laws of motion in his 1687 “Mathematical Principals of Natural Philosophy”. Consequently, the Industrial Revolution ranging from 1760 to 1820 or 1840 was born. Finally, these mechanistic viewpoints had led Laplace (1749 - 1827) to believe there is a permanent order in Nature.

With the above background information in mind, it is understandable that NGQ has been of great interest to historians of science, medicine, and natural philosophy worldwide. Numerous answers, including an interesting one offered by Needham himself, have been proposed. In his volume 7 part II, Needham believed that “One factor which stands out above all others is the rise of the bourgeoisie for the first time in history. We may review the factors which led to it, and we may discuss the results which followed from it, but it is the rise of the bourgeoisie in Western Europe from the 15th century onwards which decided that Europe would not continue trying to emulate its classical past, nor evolve in Chinese fashion, improving its technology and making small advances in various sciences without actually coming to grips with scientific method, but would strike out in a new direction, developing capitalism, scientific method and the industrial revolution one after the other” (Needham et al., 2004).

Apparently, his answer and most of the others have been sought from the disciplines outside of science and technology per se. For instance, origins such as Chinese language, script, economy, society, geography, climate and/or political systems have also been blamed for the overtaken of levels of the TCNP by Western experimental philosophy. However, it is the belief of this author that NGQ was originally posed in the fields of science and technology and an accurate answer should be acquired within them, if possible. One should not invoke the secondary or tertiary factors of social, political, and/or economic origins until proven otherwise. Moreover, the same answer will have to be able to explain why it was much more efficient than the European West in applying human knowledge of Nature to useful purposes for more than 18 centuries. Hence, the factor of the so-called “mercantile culture” proposed by Needham himself could not be an accurate one (Needham, 1969).

It is proper and fitting to mention in the introduction that in an article of his book, by comparing the contrasts between China and the West, Needham actually insightfully made an interesting remark that “the Chinese physical world view is wave instead of atom and continuum instead of discontinuity” in modern physics and sciences (Needham, 1969). This is actually an important point worthy of serious consideration later. Unfortunately, he then pointed out that “the conception of wave motion … seems sometimes to have acted in an inhibitory way upon the advance of scientific knowledge” (Needham, 1969). Quite on the contrary, when we look back nowadays, the aforementioned theories from Galileo to Laplace are not flawless or without being misleading. For instance, it is now clear that Galileo’s results are false. Kepler’s three laws are only approximations. Newton’s three laws are useful for man-made objects at most and cannot explain natural phenomena. Finally, the Laplace’s view is definitely erroneous due to the newly developed chaos theory. All of them can now be falsified. Hence, the examples of modern science given by Needham cannot be hailed as sustaining or successful. Actually, it is the purpose of this review to propose three “mathematical principles of Chinese natural philosophy” based on the “chaotic wave theory of fractal continuum” (CWTFC) so that the Chinese physical world view can be put on a firm and rigorous basis (Chang, 2012; Chang, 2013a; Chang, 2013b). It is believed to be much closer to reality than its modern Western counterpart. In the same vein, this review will also compare TCM with Western medicine in a later Section. Using the same principles, TCM and TCNP can be integrated under the same mathematical foundation. It is then hoped that the ancient scientific and medical achievements of China which have existed for more than eighteen centuries and have been stopped only three centuries ago can be revitalized and continued.

This review paper will be organized as follows. At first, TCNP is reviewed. Then, its mathematical principles based on CWTFC will be proposed. Applications to TCM and natural sciences are then covered. In order to compare with its Western counterpart, important concepts in modern Western sciences and medicine are also reevaluated. Afterwards, the so-called NGQ can be answered accurately. As an upshot, the TCM, TCNP and its sciences can finally be unified under the proposed three mathematical principles.

TCNP deals with cosmology and ontology of Nature itself. At the outset, let us translate the basic ideas of TCNP in terms of modern language. The universe is believed to be a dynamical system, called Qi, which has already existed in its present form and is still in a ceaseless Yin-Yang or back-and-forth motion (Chang, 2010a; Chang, 2010b; Chang, 2011c; Chang, 2012). Consequently, various periodic or rhythmic activities are produced and new rhythms can also emerge from such complex interactions. One of the consequences is, for example, the diversity in various species of plants, animals and minerals. In order to categorize the diversity in terse term, Five-Phases, turned out to be a good candidate. Human kind, in the theory of TCNP, is just part of the universe and should achieve harmony with other species in Nature from the viewpoints of Lao Tzu and Chuang Tzu.

After a long period of careful observations in cosmology and astronomy, the ancient sages soon realized that most of the time, regular motions of the celestial bodies were rather rare; complex and chaotic motions were the norm. For instance, Chinese lunisolar calendars were devised so that the incommensurability of the cycles involving the relative motions of sun, moon and earth could be reconciled (Chang, 2010a; Chang, 2010b; Chang, 2011c; Chang, 2012). In the ancient Chinese agrarian society, the prevalent model of space in TCNP is an interconnected continuum with ceaseless random rhythmic motions embedded in it. The earthly time is derived only from the relative motions of sun, moon and earth in the space. As a result, time is relative in the sense that it will make sense and comprehensible only through the cyclic motions of celestial bodies in space, otherwise it does not make sense. To summarize, the space and time in TCNP which contains the basic ideas of Qi, Yin-Yang and Five-Phases, cannot be separated and they are not independent of each other.

The interpretations of Qi, Yin-Yang, and Five-Phases of the last paragraph were very primitive even though they were holistic and integrative in nature. For the first eighteen centuries, they were self-sufficient and had been very efficient in applying them to useful purposes. However, in order to respond to the modern criticism of these concepts as being pseudoscientific, a rigorous mathematical representation of them is imperative. Fortunately, a modern characterization has been proposed recently, but for the sake of completeness in this review paper, some of the important details will be briefly repeated in the next section (Chang, 2010a; Chang, 2010b; Chang, 2011c; Chang, 2012; Chang, 2013a; Chang, 2013b).

Recall that the concept of space in TCNP was previously described as an interconnected continuum which has already existed in its present form since antiquity. This viewpoint is certainly different from the so-called “big-bang theory”. The comparison between these two different views will be covered in a later section, but not here. In this section, our attention will be focused on the mathematical characterization of Qi, Yin- Yang, and Five-Phases in modern dynamical terms. Only after that, we shall be able to understand how the seemingly random rhythmic motions characteristic of the universe were generated and the real meaning of CWTFC.

First of all, let us start with the concept of “Qi” (Chang, 2010a; Chang, 2010b; Chang, 2011c; Chang, 2012). This Chinese character is actually a pictogram indicating water evaporates and becomes clouds. Hence, Qi itself is related to part of the water cycle. In terms of modern dynamical system, Qi represents both (1) the fractal continua of vapor and water, and (2) the complex dynamics of phase changes in the water cycle. It is then proper and fitting to define Qi as a mathematical dynamical system, characterized by a mathematical triple (M,μ,ϕ_t ) , where M denotes a fractal continuum or the collection of state variables describing it (Chang, 2010a; Chang, 2010b; Chang, 2011c; Chang, 2012). Here, μ stands for a measure on M and ϕ_t :M → M a one parameter group of continuous, measure-preserving transformation on M .

As to the concept of Yin-Yang, it was referred to two fundamental actions in the dynamical system, now one dominating, then the other, in a wave-like succession (Chang, 2010a; Chang, 2010b; Chang, 2011c; Chang, 2012; Needham,1956). Another possible way is to use a hyperbolic operator on the phase space. For example, the phase space M can be modeled as{(x, y)(mod 1)}, i.e., a torus representing the phases of two competing rhythms endowed with measure μ = dxdy , and the hyperbolic Yin-Yang operator can be denoted as ϕ(x, y) = (2x + y, x + y)(mod 1) (Chang, 2010; Chang, 2011c; Chang, 2012). Generally speaking, a hyperbolic operator on compact space can generate various periodic rhythms and sometimes chaotic motions. Through this type of representation, the ancient Chinese descriptions of Qi and Yin-Yang can be visualized as a dynamic system with a hyperbolic flow or map.

As to the concept of Five-Phases, it can be associated with the Markov partition on the torus M equipped with the Yin-Yang hyperbolic map (Chang, 2010a; Chang, 2010b; Chang, 2011c; Chang, 2012). This hyperbolic flow ϕ is actually topologically semi-conjugate to the sub-shift of finite type determined by the As a result, the hyperbolic map of Yin-Yang can generate Five-Phases, i.e., the Markov partition of M. The symbolic dynamics associated with A, a sub-shift of finite types, can be used to study the dense periodic orbits, topological transitivity, and mixing of the dynamical systems, i.e., Qi in general. It is noteworthy that admissible trajectories can be generated by using this transition matrix A in terms of symbolic dynamics. If the initial frequencies of two interacting rhythms are not commensurable, then their relative phase trajectories as functions of time will trace out a dense orbit in the phase space M, the first hallmark of chaotic wave theory. On the other hand, if the two frequencies are commensurable, then their relative phase trajectories will trace out a periodic orbit in the phase space M. It turns out the periodic orbits are also dense, the second hallmark of chaotic wave theory (Chang, 2010a; Chang, 2010b; Chang, 2011d; Chang, 2012). It is clear by now that these ancient terse concepts can be represented in terms of modern dynamical systems, the CWTFC. Of course, the ancient sages did not have enough mathematical tools to make their thoughts more transparent.

Another important tool in dealing with the complex dynamics of TCNP is the ancient idea of correlative thinking as noticed by Needham (Needham, 1956). It should be emphasized here that, in the reductionist approach, if one cause produces a single effect, then the approach of logic can be invoked to study the cause and effect. However, if both causes and effects are manifold and intertwined, then the problem becomes very complex and logic is simply powerless. On the other hand, using the correlative thinking from one complex dynamical system to another similar one can be quite useful as long as the two systems are topologically conjugate (Chang, 2010a; Chang, 2010b; Chang, 2011d; Chang, 2012).

In previous section, the concepts of Qi, Yin-Yang and Five-Phases have been mathematized in the so-called CWTFC. In order to help us derive more important results in TCM, TCNP and its sciences, we will propose the following three laws in the context of CWTFC (Chang, 2010a; Chang, 2010b; Chang, 2011a; Chang, 2011b; Chang, 2012): Nature is considered as a continuum of multi-level functionality and it is statistically self-similar with the scale of each level. Its motion at each generic point of each level in the continuum can be described by the following three laws.

First law:

Under no external influence of radiation or matter, the first component X(t) in the state of a generic point (X(t),Y(t),Z(t)) in the continuum, as a function of time, t > 0 , takes the following form: where is a sequence of independent, identically distributed standard complex Gaussian random variables. This expression is similarly defined for t < 0. The other two components are also defined in the same way

Remarks:

(1) Notice that the summation will not converge in the sense of almost surely or L² , but once we integrate it, it will exist in both senses (Paley and Wiener, 1934). (2) Newton’s first law allows no motion or only linear motion. It is a special case of this one. (3) In our case, various modes of oscillations in the continuum of Nature are allowed. (4) A noteworthy idea is the concept of self-similarity. It is stated in the beginning that Nature is statistically self-similar with the scale of each level. Hence, this concept has broken the boundary of macroscopic and microscopic viewpoints of Western sciences. After all, there is no clear-cut boundary between these two views anyway. (5) This law is a realistic description of natural phenomena, from the pragmatist philosophical viewpoint, that it can be used to describe the phenomena all the way from the largest-scale of astronomy to geology, human beings and to the smallest-scale in a continuous fashion.

Second law:

Under external influence of radiation or wave interaction, the continuum can self-organize and the first component X_H(t) in that state (X_H(t),Y_H(t),Z_H(t)) of a generic point in the continuum, as a function of time takes the following form: for t > 0 where X_H(0) = X(0) and 0 < H < 1 . This expression is similarly defined for t < 0. The other two components are also defined in the same way.

Remarks:

(1) Notice that this expression X_H(t) is reduced to X(t) for H = 1/ 2 . (2) Moreover, for the region 1/ 2 < H <1 , the continuum is positively correlated (Mandelbrot and Van Ness, 1968; Samorodnitsky and Taqqu, 1994). One excellent example in modern physics is that this condition corresponds to coherent laser and a generalized uncertainty principle for laser can be derived for positive correlation (Chang, 2011b; Chang, 2011c). As for TCM, this second law can be used to illustrate the coherent neurological behavior during micturition as illustrated in a later Section on TCM. For the region 0 < H < 1/ 2 , this state of equilibrium corresponds to negative correlation, and a new comparable formula for blackbody radiation can be derived without quantization of energy (Chang, 2011a). The details will be described in later Sections. In the pathology of TCM, this condition will correspond to difficulty in micturition as will be illustrated later. (3) It is noteworthy that this formula implies nowhere differentiability as opposed to the twice differentiability in Newton’s second law.

Third law:

Under external influence of matter, the response or action of continuum depends on the common spectral bandwidths of both the matter and the continuum itself. The sum of the overlapped (response) and non-overlapped (no-response) spectral regions will add up to 100 percent.

Remark:

The third law indicates, in a certain sense, that the action and reaction will add up to 100 percent depending on their relative bandwidths. In Newton’s third law, “action equals reaction” will not be always true in our case.

After these three laws have been stated, it is time for us to apply them to TCM first.

The basic concepts of Qi, Yin-Yang and Five-Phases in TCNP are also the basic ones in TCM as expressed in Huang Ti Nei Ching more than two thousand years ago. One plausible explanation is that human being was viewed by ancient sages as a microcosm which is part of the universe, a bigger macrocosm. Furthermore, it was believed that deeper understanding of the complex dynamics of human body might be achieved by studying the universe via correlative thinking, and vice versa (Needham, 1956). Although it was clearly understood that the detailed materials and structures of these two cosmos were not the same, yet the dynamics of these two systems might be derived from the same mathematical principles of TCNP via the concept of topological conjugacy. It turns out that the study of rhythms in both cosmos can be associated in terms of the concept of topological conjugacy if there is a homeomorphism between these two. As a result, the contents of TCM from physiology, pathology, diagnostics to treatment can be derived and unified in a quantitative manner using the three laws of TCNP as stated in the previous Section. That is to say, the mathematical approach based on the CWTFC can be used to unify both the TCM and TCNP.

A few words of caution on anatomy should be mentioned before we proceed. The reason that TCM has not paid too much attention to anatomy is that even though the skin, bones and muscles are still maintained in the corpse, however, the blood flow and nerve innervations have already stopped. Actually, the circulatory and nervous systems are the two most important systems of physiological functions that distinguish a man from being alive or dead. Consequently, it is generally believed that dynamic conditions of physiology cannot be revealed by anatomy. The old adage that “dead men tell no tales” holds true in TCM. That is the reason why TCM has paid more attention to physiology and has used nature as a great teacher from the very beginning.

We will start out now with TCM’s ideas on physiology, and all the way to the therapeutics of acupuncture and Chinese herbology. In concert with our planet, the circadian, monthly, and seasonal rhythms of TCNP were slowly discovered. In addition to the long cycles, short physiological rhythms in humans were also noticed in TCM. For instance, the rhythms of heartbeat, radial arterial pulses, respiratory system and bladder contraction during micturition were also ubiquitous in daily lives (Chang, 2004; Chang, 2008a; Chang, 2008b; Chang, 2009; Chang, 2010a; Chang, 2010b; Chang, 2011c; Chang, 2011d; Chang, 2012). These rhythms interact among themselves and also with the outside environment. As a result, the ancient TCNP and TCM were all focused mainly on the collective interactions of various periodic rhythms at the outset. It is understandable that, due to lack of mathematical machinery, quantitative and detailed description of these rhythmic interactions were impossible at that time. As a substitute, qualitative and dichotomy terms were invented to describe the behavior of complex dynamical systems. For instance, concepts like Qi, Yin-Yang, and Five-Phases were invoked more than two thousand years ago to fill the gap between theory and practice.

In physiology, for instance, the word Qi was borrowed from TCNP as one of the most important ideas in dealing with the dynamical systems of human bodies. According to ancient Chinese medical cannons, the word Qi is closely related to the present-day neural system and Xue the blood and circulatory system (Chang, 2010a; Chang, 2010b; Chang, 2011d; Chang, 2012). In addition, one of the most important functional units in physiology of TCM is the so-called “meridian system”. This system will also be used later in pathology, diagnostics, and treatments of TCM. Without a true understanding of the meridian system, one will not be able to appreciate TCM. As to the essence of meridian system, it has recently been deciphered as the complex network of neurovascular bundles and their smaller branches, i.e., a fractal continuum, in the human body that connect internally with the viscera, and externally with the limbs, brain, and sensory organs via “chaotic” waves of blood flow and neural impulses (Chang, 2010a; Chang, 2010b; Chang, 2011d; Chang, 2012; Chang, 2013a; Chang, 2013b). It is not hard to support the aforementioned interpretation of meridian system either from ancient textual evidence or modern histology. In the book of Huang Ti Nei Ching, for example, it was said that the Xue (blood) would go hand-in-hand with Qi throughout the body via the network of meridians. The word Qi in the context of the medical canon was meant to be the reticular system of nerve innervations ubiquitous around the vascular trees, and the word Xue was certainly meant to be the fluid in the circulatory system. Hence, to equate meridian system with neurovascular bundles and its smaller branches is conformable to the teachings of Chinese medical cannons. In addition, based on modern histology, every primary neurovascular bundle, below the elbows and knees, contains an artery and motor nerves that are centrifugal and two satellite veins and sensory nerves that are centripetal. All of these units are enclosed in a connective sheath to form a neurovascular bundle. This is the reason why the primary meridians that are located below the elbows and knees have been claimed to be the neurovascular bundles (Chang, 2010a; Chang, 2010b; Chang, 2011d; Chang, 2012). To sum up, this complex network of meridian system, anatomically, is a fractal continuum with statistically self-similar structure. Functionally, there are also several major differences between the conception of neurovascular networks in TCM and Western medical physiology.

First of all, the neural system and circulatory system are inseparable in the studies of TCM (Chang, 2011d; Chang, 2012; Chang, 2013a; Chang, 2013b). When the function of one system is impaired, the function of the other one is also influenced. In TCM, it would be stated as if Yang or the neural function is impaired, then the Yin or circulatory function will be influenced. Clearly, this is, again, a manifestation of the Yin-Yang concept in TCM. Secondly, it is believed in TCM that the complex network of neurovascular bundles is connected internally with the viscera, and externally with the limbs and sensory organs. So, each organ of the human body is connected with one another through the neurovascular bundles and cannot be treated separately. This is the true meaning of the so-called holistic or integrated viewpoint of TCM. Thirdly, it is believed in TCM that the circulatory system forms a closed circuit and the neural system is also a reticular network. The circulatory system is easier to understand, but as to the reticular network of nervous system, it is not that clear or easy to see. Notice that it is also much harder to detect the weak electromagnetic fields of this neural network. However, this ancient reticular viewpoint of TCM is not totally baseless as can be seen from textbooks of modern histology (Sharpey-Schäfer, 1914). For example, the endings of sensory fibers that are distributed to the Pacinian corpuscles, tactile corpuscles and end-bulbs usually terminate after a convoluted course within these organs. In addition, it has also been found that the terminal motor nerves into the muscle cells ending within them in loop-like expansions (Sharpey-Schäfer, 1914). Hence, the distal ends of both the motor and sensory nerves form networks of loops and convolutions. As to the proximal ends of human cortex in the central nervous system, numerous fibers of the myelinated nerve fiber network can also be observed not only in the white matter but also in the gray matter with large size via the Weigert-Pal staining method. This result has clearly indicated that the proximal and distal ends of the nervous system are both reticular networks of nerve fibers. Therefore, the neural system is indeed conformable with the TCM viewpoint: a circuit of reticular network.

Quantitatively, the complex network of neurovascular bundles and its smaller branches can be characterized by its distributed conductance (G), resistance (R), inductance (L), and capacitance (C) as functions of space, time, and frequency (Chang, 2011d; Chang, 2012; Chang, 2013a; Chang, 2013b). Data supplied by two studies were used to plot the longitudinal impedance diagram of the squid giant axon membrane and the input impedance diagram of the ascending aorta of a dog, respectively (Chang, 2011d; Chang, 2012; Cole, 1968; Mcdonald, 1974). The longitudinal impedance of a nerve fiber is basically inductive at low frequencies and capacitive at high frequencies. On the other hand, the input impedance of an aorta is capacitive at low frequencies and inductive at high frequencies. Again, this is a manifestation of the Yin-Yang concept in TCM.

In physiology of TCM, once we have clarified the concepts of Qi, Yin-Yang, Five-Phases and meridian system, then one will need to show the interconnectedness of the meridian system with limbs, sensory organs, and visceral organs. Recently, the aforementioned physiological concepts have been successfully verified (Bernardo-Filho et al., 2014; de Souza et al., 2014). Henceforth, we can study the most important issue in physiology of TCM: the Qi-hua problem. To put it in modern language, it is equivalent to ask how the physiological functions can proceed normally in human bodies. To illustrate, the functions of urine storage and micturition of lower urinary tract will be used to exemplify how these physiological functions can proceed normally. The three laws will be invoked to mathematize this problem. In particular, the concepts of fractal dimension (FD) and spectral measure of the second law in TCNP will be invoked frequently. Here, the Qi-hua problem in the lower urinary tract can be equated with the statements of how the urine can be properly stored and voided when required.

Recall in the second law, it was stated that “Under external influence of radiation or wave interaction, the continuum can self-organize and the first component in that state( X_H(t), Y_H(t), Z_H(t)) of a generic point in the continuum, as a function of time takes the form of X_H(t) as defined in the earlier Section. In order to use the parameter H and spectral frequency to characterize the Qi-hua problem, we have combined these two important indicators, i.e., FD=2-H and spectral frequency in studying the cystometrogram (CMG) of bladder and EMG of external urethral sphincter (EUS) during micturition of female Wistar rats (Chang et al., 1999; Chang et al., 2000; Chang et al., 2004; Chang et al., 2007). In order to obtain these two quantitative indices, a novel method based on the spectral distribution function is briefly described here (Chang et al., 2007). The steps are divided into two parts. The first part is to create a database, and the second one to estimate FD with the aid of the database. First of all, in the database creation stage, the following six steps are taken:

Step (1) Start with an empty table; choose the window-size and K (number of terms of odd Legendre Polynomials (LPs). Step (2) Increase H with increment 0.0001 from 0. Step (3) Calculate the autocorrelation function (ACF) of the difference of original physiological signals for each H, and then find its spectral distribution function (SDF) Step (4) Fit SDF with K odd LPs and get K fitting coefficients Step (5) Save those coefficients in the database. Step (6) When H reaches 0.9999, the whole database is obtained.

Next, in the FD estimation stage, the following nine steps are taken.

Step (1) Set the signal as the discrete difference of signals in the beginning. Step (2) Set the window size as 1 s or 500 points. Step (3) Calculate the ACF of the signal and then its SDF. Step (4) Fit SDF with K odd LPs and get K estimated coefficients Step (5) Evaluate distances between the estimated coefficients with coefficients in the database. Find the most suitable H by the least-square distance criterion. Step (6) Set D = 2- H. Step (7) Shift the processing window one point to the right until the window have covered the last 500 points of the time series

If the last window have been covered and processed, go to next step. If not, go back to Step (2).

Step (8) Find the mean and variance of the resultant D. Step (9) Test if the input signal is indeed discrete time Gaussian noise by two thresholds: │mean│-1 < 0.1 and variance< 0.01. Output the result and terminate the program if the two inequalities are not satisfied. Otherwise, take the difference operation on the signal and go back to Step (1).

Now, let us apply these algorithms to the lower urinary tract that includes both the bladder and EUS so as to understand the first part of Qi-hua problem, i.e., micturition. It is well-known that the bladder consists of smooth muscles and is innervated by hypogastric and pelvic nerves. The EUS consists of striated muscles and is innervated by pudental nerves. We have observed that for intact rats, the rhythms of the EUS and the bladder are synchronized around 7 Hz, and their FDs are both under 1.5 during voiding in order to facilitate the micturition process (Chang et al., 2000; Chang et al., 2004). Here, we have used the algorithm to examine the signal frequencies and persistent signal intensities in terms of FDs of both EUS and bladder at the same time. Under these two criteria, we can say that the first part of Qi-hua or micturition has no difficulty

As to the second part of Qi-hua problem of the lower urinary tract, we have to examine the urine storage problem so as to make sure there is no urine incontinence (Chang et al., 2009). Some of the details will be briefly stated here. Just like the case of micturition, the first index of FD can be used to characterize the collective intensity of nerve innervations and the second the rhythms of physiological signals. Here, the primary aims are to (1) examine if the involved muscles in the lower urinary tract would be under similar co-activations during the urine storage phase, and (2) characterize quantitatively the sympathetic and parasympathetic nerve activities simultaneously. Experiments have been performed on adult female Wistar rats and then the EMG of EUS and CMG of bladder have been analyzed. Results have indicated that the EUS did not participate in the storage phase. Actually, it has been elucidated by its FDs (1.5918 ± 0.0157) indicating no appreciable amount of signal intensities in the EUS. On the other hand, the bladder has exhibited parasympathetic frequency of 8 Hz with signal-to-noise ratio (SNR) = 19.9001 decibel (dB) for group mean, and sympathetic frequency of 19 Hz with SNR = 22.8330 dB for group mean. In addition, its FDs (1.4796 ± 0.0092) have indicated relatively persistent intensities during storage, as compared to that of EUS (1.5918 ± 0.0157) with statistical significance (p < 0.01). Hence, it can be concluded that the EUS has not been activated during the phase of storage. The bladder, after careful examination of the results, is actually under the cooperative, not antagonistic, sympathetic and parasympathetic nerve activities with discernible rhythmic frequencies and persistent intensities as indicated by the FDs (Chang et al., 2009).

To sum up, in the bladder Qi-hua example, we have shown that (1) the bladder can hold urine in the storage problem under the cooperation of sympathetic and parasympathetic nerves, and (2) the bladder can void urine smoothly and synergistically with the EUS, using the two indices FD and spectral function from the second law of TCNP. It is believed that the Qi-hua problems of other visceral organs in TCM can be similarly studied.

Next, in pathology of TCM, the problem is again reduced to the functional level and can be formatted as Qi-hua is not able to be performed properly. In the example of lower urinary tract, it can be equated with the cases that either bladder has urine incontinence problem or has difficulty in micturition. Notice that in TCM, the pathology has to do with only the functional disorder not structure abnormality. As a result, the anatomic pathology, microbiology and chemical pathology of Western medicine have no places in TCM. The comparison of pros and cons of TCM and Western medicine will be covered in a later Section. For here, we will focus on the functional disorder during the micturition process. For spinal cord injury rats, we need both the FD and spectral distribution function to differentiate normal from pathological cases. There are actually two different types of pathological contractions during micturition. One is the so-called “non-voiding” contraction, and the other “abnormal” voiding contraction. The non-voiding contractions are seen in some rats, but not in all. If they occur, they are usually in the filling phase. Hence, this is one of the pathological conditions. For the spinal cord injury rats, however, the voiding contractions usually have much more residual volume of urine left in bladder. The results in computing FD and spectral distribution function can be summed up as follows. In the non-voiding contractions, no temporal coherence in FDs and no significant frequency components exist between EMG and CMG. Yet, for abnormal voiding contractions, the FDs are not coherent; however, the rhythms may be synchronized but may appear in an impaired or weakened way. As a result, our quantitative criteria of FD and spectral distribution function have been used successfully in the pathological description of TCM.

Then, in the diagnostics of TCM, the human body is considered as a hierarchical organism consisting of many levels of mutually interacting physiological systems. The hierarchy exists not only in structure and function, but also in space and time. In order to diagnose and then treat diseases of such a complex hierarchical system, the conventional reductionist viewpoint has to be replaced by holistic perspective emphasizing the collective behavior of rhythmic interactions and their emergent properties. The first step to achieve that goal is to collect both the external and internal information of patients via the following four basic steps: (1) visual inspection of the patient’s external demeanor and bodily motions; (2) auscultatory and olfactory examinations of the patient’s voice, odor, and scents; (3) direct dialogue with the patients concerning their subjective feelings of the emergent feelings of pain, appetite, insomnia, living habits, etc.; and (4) involved palpation of the patient’s peripheral arterial pulses that contain the information of the blood flow, nerve innervations, local impedances resulted from the combined states of heart and other internal visceral organs. After collecting the physiological and psychological information with regard to the collective symptoms or syndrome of the patient, the TCM clinicians have to come up with a conclusion of the present states of the patients. Integrative and yet terse descriptions, such as Qi Deficiency, Blood Deficiency, Qi Excessiveness, Blood Excessiveness, Qi Hindrance and Blood Hindrance, etc., have been devised to describe the states of the patient. However, due to lack of modern recording devices, most of the collected physiological and psychological information, in ancient time, could not be quantified and analyzed so as to support their integrative descriptions in TCM. As a result, these integrative descriptions have always been treated as pseudoscientific and could not be justified from a modern medicinal viewpoint. Fortunately, recent advances in modern recording devices and mathematical machinery have enabled us to start recording some of the physiological data and interpreting them in terms of holistic descriptions. To demonstrate, let us use human forearm pronation as an example to quantify the concepts of Qi Deficiency, and Qi Hindrance in limb muscles (Chang et al., 2008a). The muscles in the illustration includes the following ones of the upper arm: (1) short head of biceps brachii, (2) long head of biceps brachii, (3) brachialis, (4) lateral head of the triceps brachii, (5) brachioradialis, (6) pronator teres. In the mean time, an electrogoniometer was taped on the lateral sides of the forearm and upper arm to measure the flexion angle. The surface EMGs of the aforementioned muscles were collected and analyzed. The upshot was that the surface EMGs, temporal FDs of these six groups of muscles, during normal forearm pronation, have all been under 1.5 and exhibited the same synchronization frequencies. Under these two quantitative indices, the Qi of this subject can be considered as being normal for this case. As to the case of a volunteer whose forearm has been passively pronated, results have indicated that all of the spectral amplitudes in the muscle EMGs were small and no prominent frequencies could be found during the whole pronation process. Moreover, FDs were not under 1.5, but only around the values of 1.6. Under these two quantitative indices, the state of this subject can be diagnosed and labeled holistically as being Qi Deficiency. Here, Qi is referred to the collective behavior of neuromuscular activities characterized quantitatively by FDs and rhythms of these muscles, and Deficiency is indicative of: (1) the collectively weak and incoherent intensities of all EMGs as indicated by their FDs around the neighborhood of 1.6; and (2) the loss of overall synchronizations in rhythms. In this way, the ancient holistic notion of a diseased state Qi Deficiency can now be characterized quantitatively. Finally, in the case of a radial-nerve- palsy patient, the analysis of the EMGs of the same six group of muscles have indicated that all of the spectral amplitudes in the muscle EMGs were very small, the same as the previous case, and no prominent frequencies could be found during the whole pronation process. Moreover, FDs have exhibited the range values to be around 1.8. Under these two quantitative indices, the state of this subject can be diagnosed and labeled holistically as being Qi Hindrance. Here, Hindrance of Qi is indicative of the collectively weak and incoherent intensities of all EMGs as indicated by their FDs around the neighborhood of 1.8; and (2) the loss of overall synchronizations in rhythms. Notice that the three types of conditions on Qi: (1) normal, (2) deficient, and (3) hindered can be distinguished from multiple comparison test of their respective population marginal mean values (Chang et al., 2009). Henceforth, the holistic descriptions of diagnostics in TCM can now be placed on a rigorous footing. One has to keep in mind, however, that in the TCM diagnostics, indispensible psychological information and mental states that can only be revealed by the patients are gathered but they are still very difficult to quantify by modern equipments up to now. A unique feature of TCM is that the information revealed by the patients has played a vital role in the clinician’s decision on the states of patients.

One of the important advantages in using such holistic descriptions in TCM is that the countermeasures or strategies of treatment can be laid down immediately after the diagnostics is completed. Depending on the diseased states of patients, doctors can use one or several of the following eight countermeasures in their herbal remedies or acupuncture treatment: (1) to induce sweating so that poisons or bacteria, if exist, can be expelled and high fever alleviated; (2) to induce vomiting via activating the autonomic nervous system so that poisons or indigestible stuff in the stomach can be expelled; (3) to induce purging so that poisonous stuff in the abdomen can be expelled; (4) to activate the defense system so that bacteria, if exist, can be expelled; (5) to induce motility so that the sluggish body functions can be improved; (6) to remove congestion, or full or partial blockage of internal organs via adjusting meridian system so that normal states can be resumed; (7) to tonify the human body due to depletion of energy or exhaustion; and (8) to harmonize the discord so that the normal physiological and psychological states can be restored (Chang, 2013a; Chang, 2013b). Based on the aforementioned principles of treatment, let us elucidate why acupuncture with just one needle can heal so many different physiological disorders.

In clinical treatments, the technique of acupuncture has been recommended by World Health Organization (WHO) Consultation on Acupuncture (WHO, 1991). According to one of its reports, more than 100 indications can be treated by acupuncture in clinical practice (WHO, 2002). The onehundred indications in that report covered a wide range of physiological disorders. They could be divided into the following 14 different types of malfunction: pain, infection, neurological disorders, respiratory disorders, digestive disorders, blood disorders, urogenital disorders, gynecological and obstetric disorders, cardiovascular disorders, psychiatric disorders and mental disturbances, pediatric disorders, disorders of the sense organs, skin diseases, and cancers. In this section, the concept of meridian system, based on CWTFC, will be used to elucidate the mechanism of acupuncture analgesia and therapeutics, respectively (Chang, 2012; Chang, 2013a; Chang, 2013b).

To explain the mechanism of acupuncture analgesia, one has to know the definition of pain first. It was defined by The International Association for the Study of Pain as “an unpleasant sensory and emotional experience which we primarily associate with tissue damage or describe in terms of such damage, or both”. This definition basically associates pain with tissue damage. However, in TCM, pain need not be due to tissue damage. For instance, in the phantom limb pain, tissue does not exist anymore. On the other hand, tissue damage may not cause pain. For instance, acupuncture can cause tissue damage, yet it achieves pain relief. Furthermore, there is no need to have a dedicated nociceptive system in conducting pain signals. The meridian system or neurovascular network per se can conduct and transmit nerve signals irrespective of whether it is pain or not. In TCM, pain is mainly due to the stagnation, full or partial blockade of the normal neurovascular flows which may or may not result from tissue damage. If the flow is blocked at the skin level, bruising or swelling of the tissue will be observed. Blockage at the flesh level will produce stiff, sore muscles. Stagnation in the joints will produce arthritis pain. Internal neurovascular blockages or abnormal flows will produce many kinds of pain, including headaches, sore throat, chest pain, stomach pain and menstrual pain. If the stagnation or blockade of the neurovascular flow in that part of the body is removed, then the pain syndrome will also disappear (Chang, 2013a). In terms of the CWTFC proposed in an earlier section, pain, i.e., the stagnation or blockade of the neurovascular flow can be characterized by its abnormal impedances. For example, phantom limb pain is derived from the amputation modifying the original neurovascular flow and changing the limb impedance to a different value. If this value can be adjusted and matched with that of the remaining part of the body after a certain amount of time, the pain will go away. It was contended in Kenneth Cole’s book that the injury current will trigger electromagnetic inductive effects so that the impedances will change (Cole, 1968). In our case of acupuncture, the impedances of correlated neurovascular bundles due to acupuncture at an acupoint will also induce drastic changes of the local impedances. Two consequent scenarios are possible. (1) If the impedance of the meridian hugely mismatches with that of the brain after acupuncture, then the traveling wave of pain signal will be largely reflected back and only partially transmitted to the brain, hence pain relief can be achieved. (2) If the impedance of the meridian entirely matches that of the pain source after acupuncture, then the pain source would appear to be nonexistent to the brain, hence analgesia can be achieved (Chang, 2013a). The former mechanism can be used to explain the relief for chronic pain and the latter one for acute pain. As to the efficacy of pain relief and analgesia, sometimes acupuncture works so quickly in tens of seconds. This fact is extremely difficult for the biochemical approach to explain why the local release of endorphins or adenosine can have a distant effect in such a short amount of time (Goldman et al., 2010; Han, 2004). However, for the proposed mechanism, the impedance change can indeed modify the traveling wave of the neurovascular network both locally and globally in a short amount of time. Consequently, both local and distant acupuncture effects can be explained under the same principle of wave or field approach. This is another advantage of the CWTFC. Finally, it should be pointed out that the meridian system of the neurovascular network is a fractal continuum and its impedances are functions of space-time and frequencies. In invasive sham control or placebo acupuncture, the sham position is always located in the proximity of some neurovascular branches of the fractal network. If the injury current is strong enough, it will certainly change the impedances of near-by meridians and achieve some analgesic effects. By the same token, the invasive sham control will not produce any significant effect if its intensity of stimulation is either too weak or is decayed to an insignificant level when it reaches the relevant meridian. Moreover, the mechanism why acupuncture is so effective in treating the aforementioned 14 various types of physiological disorders or malfunctions sometimes with just one needle can also be elucidated via match or mismatch of the impedances (Chang, 2013a; Chang, 2013b). The interested readers can refer to those papers for more details.

In the treatment of using Chinese herbs, the case of “hypertension” will be used as an exemplary case. It is said that the problem of “hypertension” has affected more than a few hundred million individuals worldwide and is believed to be responsible for seven million deaths each year (Chang, 2011d). The effective control of hypertension is usually limited by adverse effects, availability, and cost of antihypertensive medications. In order to reduce the adverse effects and cost of antihypertensive medications in western medicine, modalities of complementary and alternative medicine, including Chinese herbs, have been used by patients worldwide with increasing frequency. However, due to conflict of interest, these alternative therapies have sometimes been criticized for lacking demonstrated efficacy and safety in treating cardiovascular disease and hypertension (Chang, 2011d). Nevertheless, herbs per se have been used in TCM to treat symptoms related to “hypertension” for more than 3,000 years. Today, the efficacy of Chinese herbs is well supported for treating other acute and chronic physiological disorders in addition to “hypertension” in China, Taiwan, and worldwide (Chang, 2011d). In Western medicine, patients with “hypertension” were treated with drugs to reduce their systolic and diastolic blood pressures. However, the concept of “hypertension” is actually a misnomer and much of the confusion in this field arises from the misunderstanding of some of the basic concepts in cardiology. First of all, pressure is defined to be force per unit area. It is not a robust parameter when used to measure blood pressure. It is because the pressure is a random field that its values depend on the cross sectional area of blood vessels even if the pumping force of the heart is kept relatively the same for quite a while. As we all know that the diameters of blood vessels vary continuously from main arteries to small arteries and to capillaries of the human body. Hence, blood “pressure” is going to change constantly as a function of space and time. In TCM, there is no such term as blood “pressure” for three thousand years. In TCM, it is the blood flow and its smoothness that are important. In other words, the blood pressure problem in Western medicine has always been treated as a blood distribution problem in TCM. For instance, after meals, our blood should be distributed to the digestive tract. During exercises, our blood should be distributed to peripheral limbs. Hence, it is the blood flow and how the blood is distributed in the human body that is important.

In TCM, the clinical symptoms and signs like headache, vertigo, tinnitus, dizziness, and fainting have been used to differentiate the etiology of “hypertension”. Basically, these symptoms are due to the improper blood distribution among the brain, visceral organs, and peripheral limbs. In addition, the nerve innervations of the blood vessels, often called Qi, go hand in hand with the blood. For instance, according to TCM, when one lies down at night, then the blood flow in the peripheral limbs can return to visceral organs. After meals, one should avoid studying or performing strenuous physical exercise immediately so that blood will go to the digestive system. On the same basis, too much stress and anxiety will also disrupt the proper blood distribution in the head and will cause headache, vertigo, tinnitus, dizziness, and fainting. To sum up, the etiology of “hypertension” according to TCM is mainly due to the improper blood distribution in the human body that has to do with the nerve innervations, i.e., Qi, and blood distribution.

In the treatment of Western medicine on hypertension, the individualized choices of drug therapy include the following five major classes: diuretic, beta blocker, alpha blocker, calcium blocker, and angiotensin-converting enzyme inhibitors (ACEI). In the first class of diuretics, side effects include a number of biochemical changes such as a decrease in plasma potassium and increase in glucose, insulin and cholesterol. The side effects of beta blockers during pregnancy include fetal growth retardation. The calcium blocker will induce flushing and ankle edema. As to the ACEI, side effects are also abundant, such as rash, loss of taste and leucopenia. It is believed that the designs of these drugs are based on the fundamental misunderstanding of the etiology of “hypertension” and how the autonomic nervous system works. According to our preliminary studies of micturition and storage of urine in rats, i.e., the Qi-hua problem in lower urinary tract, and acupuncture effects in humans, the sympathetic and parasympathetic systems of autonomic nervous system are cooperative not antagonistic (Chang, 2009; Chang, 2011d). Consequently, the drug designs using the concept of “inhibition” completely miss the point.

On the other hand, the herbal treatment of hypertension in TCM is based on a completely different philosophy. It is the blood distribution among different parts of the body that is the utmost important thing, not the blood pressure at all. Moreover, it is believed that the visceral organs should work together cooperatively rather than antagonistically. For instance, the liver, spleen, kidney, heart and limbs all need blood flow while the total amount of blood volume is a constant. It is essential to distribute the right amount of blood to the right place at the right time. The philosophy of herbal treatment in TCM is basically that of making sure the blood flow is smooth and if there is any stagnation or hindrance in the brain, visceral organs or meridian system, drugs that are made of natural herbs will be used to remove the stagnation. In addition, the natural products are optically active so they have therapeutic effects.

It was mentioned that TCNP believes that human beings are just part of the universe and should achieve harmony with it. As to the natural philosophy of the West, modern emphasis has been less on a passive observation of Nature’s activity. Instead, the emphasis has been shifted to the control exercised through experimental observation for the sake of control of nature. With regard to nature itself, the school of Leucippus and Democritus regarded the world as a bunch of lifeless atoms in a vortex, and this school of thought has basically dominated the main stream up to nowadays even though there were some modifications of the original ideas along the way, but the basics have been remained the same. Hence, the Western natural philosophy can be summarized as follows: (1) Nature is composed of lifeless atoms or sometimes called elementary particles, (2) The interaction of these elementary particles is basically through collision in order to have effects, and (3) Man can control nature for the latter one is only a passive recipient of the activity of the former. On the other hand, the TCNP can be summarized as that (1) Nature, including anything else, is a continuum with fractal structure, (2) The interaction is basically through wave or field in order to have effects, and (3) Man is part of nature and the former one should achieve harmony with/within the latter.

By comparing the differences of these two schools of thought, it is obvious the medicine and sciences derived from them will definitely be different. In the following two sections, we will compare the differences between Western medicine/science and those of their Chinese counterpart.

TCNP believes that nature is a continuum with fractal structure. TCM also believes that human body is a fractal continuum such that the visceral organs, peripheral limbs, sensory organs, and the brain are unified as an organic whole via the meridian system. They will influence one another so that in TCM, from physiology, pathology, diagnosis, to treatment, the whole body should be treated as a whole. For example, cardiovascular problem of the heart cannot be treated without considering other visceral organs. The interaction of these organs must have interacted via wave or field interactions in order to have physiological effects.

Recall that the meridian system in TCM has been characterized as a complex network of neurovascular bundles and its smaller branches. The blood flows in the vascular branches and the nerve innervations in the nerve bundles are all transmitted in terms of rhythmic waves. As a result, the rhythmic functions and its emergent behavior are considered more important than the morphology of the structures. This is the reason why, in the physiology and pathology of TCM, functions are more important than structures. A simple explanation is that functions can adapt even though the structure has changed somewhat. The connotation is very important in pathology. For in Western medicine, sometimes the chemical pathologists or anatomical pathologists will pay attention to minor increase or decrease of certain chemical molecules or anatomical changes of structure due to compensation. However, from the viewpoints of TCM, as long as normal functions or rhythms have been preserved or abnormal functions have not emerged, there is no need to get rid of the abnormal structures. The TCM approach will not only save a lot of expensive diagnostic cost but also avoid many false diagnoses.

Finally, TCM believes that human is part of nature and the former one should achieve harmony with the latter. The upshot is that TCM never tries to wipe out or kill all the bacteria or viruses that are considered to be detrimental to the patient by Western medicine. It is because the doctors of TCM understand that the bacteria or virus have existed in the world much longer than human beings. There is no need or possibility to kill them all or wipe them all out. As long as we keep our bodies healthy and keep the correlated bacteria or virus under certain acceptable level via acupuncture or herbs, then we will be fine. It is also noteworthy to point out that in the chemical pathology or microbiology of Western medicine, the real correlation between certain strain of bacteria or virus and that specific disease is seldom solidified. The well-known example is the HIV virus in AIDS. Moreover, even if the strong correlation can be identified, the quantity of that bacteria or virus can indeed induce such a disease was also seldom quantified. Another famous example is the DNA damage as the cancer cause and the genetic disease; so far the quantification has been scarce if not impossible. The interested readers can consult the ten principles of systems biology proposed by Dennis Noble (Noble, 2008).

As to treatment methods, TCM uses acupuncture and natural products such as herbs that are optically active and having therapeutic efficacy for patients. The herbs have been carried out on humans for more than three thousand years and have been proved to be of minimal side effects after proper handling and treatment. TCM has been from bed-to-bed for several thousand years, so there is no bench-to-bed problem as in the Western translational medicine. It is tragic and a big loss for human beings if this ancient Chinese medicinal art is totally diminished, for the patients will have lost one effective way of healing.

By far, it is fair to say that from physiology all the way through pathology to treatment, these two schools of thought are totally different. Maybe we need more time to see which one is better, but it is imperative now to encourage the doctors of Western medicine to learn TCM so that they will have more tools in their toolbox and can help their patients in a more compassionate way.

Modern sciences, according to the dentition of Joseph Needham, is the testing by systematic experiment of mathematical hypotheses about natural phenomena, He thinks that the so-defined modern science originated only in the West. The new or experimental philosophy of the West ineluctably overtook the levels reached by the natural philosophy of China, leading in due course to the exponential rise of modern science in the 19th and 20th centuries. The familiar examples given by him were (1) planetary orbits were circles proposed by Galileo (1564 - 1642), (2) planetary orbits were ellipses in the three laws of Kepler (1571 - 1630), (3) mathematical principles of natural philosophy and his three laws by Isaac Newton (1642 - 1727) in 1687 and the consequent industrial revolution around 1760 ~ 1820 or 1840, and the (4) permanent order in nature as proposed by Laplace (1749 - 1827). Now, as indicated previously, we already know that Galileo’s results are questionable, Kepler’s three laws are only approximations, Newton’s three laws cannot explain many natural phenomena and finally Laplace’s view is erroneous by the recent chaos theory. However, since 1900, the advancement of modern physics, including the quantization of energy in blackbody radiation; quantum mechanics; laser in science and technology; big-bang theory of the cosmology; atomic theory of matter, electricity and radiation; and modern technology have made the impression on many persons that Western modern sciences have been very successful and hence must be on the right track. However, for those experts in science and technology know and understand very well that there is incoherence in modern sciences per se. For example, laser has violated the uncertainty principle of quantum theory. Moreover, there are huge gaps among the disciplines of physics, chemistry, biology, and medicine. It is the time to check if there is anything inconsistent in the approaches of modern physics. Let us first quote in verbatim what Needham had in mind (Needham et al., 2004): “Encompassing Chinese thinking was the overall predilection for action at a distance, as opposed to the Western predilection for atomism. This may well have handicapped the Chinese in elaborating a theory of dynamics, but was helpful in discovering such things as the nature of the tides, of musical resonance and of magnetic phenomena.”

It is clear that if “action at a distance” may have handicapped the Chinese, then the conception cannot be “helpful in discovering such things as the nature of the tides, of musical resonance and of magnetic phenomena.” Moreover, we all know that the theories of tides and geomagnetism can never find a good explanation via atomism. Hence, it is the purpose of this Section to point out that the Chinese physical world view will turn out to be much closer to reality than its modern Western counterpart. Using the three laws in the mathematical principles of TCNP, we will be able to settle those aforementioned problems of controversy and paradoxes in the modern sciences. But before doing that, we should quote in verbatim some of the misunderstandings in the wave-particle duality or complementary principle of Niels Bohr. According to Max Born, “Bohr is in the habit of saying: the wave and corpuscular views are complementary. By this he means: if we prove the corpuscular character of an experiment, then it is impossible at the same time to prove its wave character, and conversely” (Born, 1989).

It is well-known that Western modern sciences are now ecumenical, there is no such thing as “Chinese modern sciences” as yet, but based on the mathematical principles of TCNP, which is more general than Newton’s three principles, one can derive a consistent system of modern sciences. The space in this paper is limited, so only the basic framework will be outlined as follows. First, let us recall that modern quantum theory starts out with Planck’s derivation of blackbody radiation formula. If we can derive a similar formula without using energy quantization, then the whole quantum theory would be rendered as unnecessary. Furthermore, a more general uncertainty principle is required in order to explain why laser can be invented.

First of all, it is instructive to review briefly how the Planck radiation formula was derived by him (Chang, 2011a). Planck’s original derivation of the spectral distribution of the energy density u_ν was expressed as a function of the frequency ν and temperature T by the formula u_ν =ν³ f(ν/T) via theories of thermodynamics (Planck, 1959). To determine the function f (ν /T) , Planck chose a linear harmonic oscillator of proper frequency ν such that the electromagnetic energy radiated per second by this electric dipole would be the same as the work done on the oscillator by a radiation field of spectral energy density u_ν in the case of equilibrium. According to Maxwell’s field equations, the spectral density of radiation is a function of the mean square values of the electric and magnetic field strengths E and H. To derive just one component of the electric field at a generic point in a stationary field of radiation, Planck used where C_n is some positive constant, p the fundamental period, and θ_n the phase, respectively (Planck, 1959). Using then the quantized mean energy of an oscillator, Planck obtained his famous radiation formula where h is the Planck’s constant, c the speed of light, and k the Boltzmann constant. To derive our comparable radiation formula, we will basically follow the first and second laws of our mathematical principles of TCNP that under no external influence of radiation, the component E_z(t) takes the form where is a sequence of independent, identically distributed standard complex Gaussian random variables. Now, under external influence of radiation field, the generic point in the continuum will take the following form (for H < 0.5 ):

It will be called the fractional electric (or magnetic) field with Hurst parameter H (0 < H <0.5) starting with value E_z(0) at time 0. This expression is similarly defined for the case t < 0 and will reduce to E_z(t) when H = 0.5 . After a series of complex computations, a new spectral representation of the fractional electromagnetic field can now be represented as with the Hurst exponent 0 < H < 0.5. This is our derived radiation formula (Chang, 2011a). It is fitting to emphasize here that our derivation has only assumed that the radiation field is self-similar and its increments are stationary when the system is in equilibrium. Only these two assumptions can lead us to the proposed new radiation formula without any energy quantization assumption. The essence and connotation of this derivation is to illustrate that the quantum assumption is not necessary in the derivation of blackbody radiation formula. Moreover, our derivation is equivalent to the fractional Brownian motion which is a generalization of the Brownian motion and has been a powerful tool in the derivations of atomic theories of matter and electricity. As a result, the theories of matter, electricity, and radiation have all been unified under the same notion of our second law. The advantages of our formula are manifold. First of all, the space of our system is a L² -Hilbert space and it has finite total energy. Henceforth, its increments will also be in L² and also have finite energy. Secondly, one cannot take the limit as the number of molecules tends to infinity in quantum mechanics because the finite mean energy for each degree of freedom of the molecule will make the whole system energy diverge. Yet, in our approach, the energy divergence problem can be completely avoided (Chang, 2011a).

It is also worth mentioning here that Planck’s formula can only describe the envelope of solar spectrum but not the fine details, such as tens of thousands of dips in the solar spectrum known as Fraunhofer dark lines. In standard textbooks of modern physics, for instance, the dark lines in the solar spectrum are attributed to the absorption of vapors in the solar atmosphere. Yet, the temperatures of the vapors in corona are actually much higher than those of the photosphere; hence it is not convincing to use the idea of absorption in explaining the dark lines. Furthermore, all elements in the periodic table should have been vaporized under such high temperatures. It is therefore quite questionable that we would be able to eventually identify all these more than 26,000 solar dark lines using the absorption spectra of chemical elements in the periodic table. One other paradox in astronomy has to do with the big-bang theory. If the 3K cosmic background radiation is really derived from the residual of big-bang, how come its intensities are positively correlated with the periodic cycles of sunspots? The final paradox has to do with the temperatures of sunspots. So far, no solid proof has been presented for the temperatures of sunspots to be between 4000 K - 5000 K as claimed by many astronomers.

As a matter of fact, the aforementioned paradoxes can be explained via the mathematical principles of TCNP. An easier or layman explanation is as follows. One only needs to realize that the activities of sun actually cover a very broad range of frequencies. For instance, it ranges from the lower range of radio frequency, visible light, and all the way to X-rays. Moreover, from the perspectives of our theory, the spectra of different bands are actually self-similar. Consequently, the copies of blackbody radiation envelope with different amplitude and widths in the spectral range can be present not only in the visible light region, but also in other frequency bands. The only differences are the amplitudes and frequency ranges may be varied. For instance, in the radio frequency band, the shape of the spectrum is similar except that the scale of frequency range should be in the range of 10¹¹ Hz instead of 10¹⁵ Hz, and the amplitudes may also vary appreciably. As for the X-ray band, the frequency range will be much higher than that of the visible light band. By superposing the three different bands of solar spectrum together, one can now explain the many aforementioned paradoxes in astronomy. For example, the dark lines in the solar spectrum are actually the emission lines of radio frequency band being superposed on the visible light region. In this band, the frequencies are smaller than the visible light by an order of 10⁴ . Hence, the origin of tens of thousands of dark Fraunhofer lines in the solar spectrum is actually from the spectral emission energy of the radio frequency band. As to the 3K cosmic background radiation paradox, since it is highly correlated with the activities of sunspots, we contend that its wavelength should be in the order of millimeter and frequency in the radio frequency band according to the Wien’s displacement law. Consequently, the temperatures of sunspots are really in the neighborhood of 3K, not the 3,000K to 4,000K as predicted before. This is consistent with the fact that the intensities of 3K will increase as the sunspots are more active (Chang, 2011a). An important by-product is that the big-bang theory can now be falsified and the viewpoint of TCNP is more realistic than its Western counterpart. Of course, all theories are provisional and can be accepted if they are not falsified. So far, the big-bang theory can be falsified, but not the TCNP yet. The detailed derivations will take too much space of this review paper and those results will appear in an upcoming book.

In the previous derivation of blackbody radiation, the H parameter in our second law of mathematical principles for TCNP is in the negatively correlated region of 0 < H < 0.5. In the positively correlated region of 0.5 < H < 1, a generalized uncertainty relation will be derived in the following. In this case, the increments of our fractional electric or magnetic field will be used in the derivation. Its spread in intensity can be computed through the covariance function. By using Bochner’s theorem, an uncertainty relationship can be derived (Chang, 2011c). The generalized uncertainty relationship for 0.5 < H < 1 has been obtained as ΔνΔτ ≈ kτ ^2H-1/2. Recall that in the case of maser, people like Bohr and von Neumann had been puzzled and bewildered by its violation of uncertainty principle. Here the generalized uncertainty relationship derived can be made much less than1 / 4π on the right hand side of the formula, i.e., the ultimate quantum limit. Hence, this uncertainty relation is much more general than the one in quantum theory for the former one can explain why laser can be a strong coherent source of light with narrow bandwidth and short pulse duration. In addition, this equation can also be used to predict the ultimate limit of bandwidth and strength of laser source given the time span of the pulse. It is worth mentioning that in the same vein, the essential limits in the synergy of physiology can also be obtained.

As to the photoelectric effects, our results can successfully explain both the normal and selective effects while Einstein’s model cannot explain the selective effect at all. As an illustration, the blackbody radiation curve can also be viewed as the spectral characteristics of any band pass filters of almost periodic structure of matter, say metal, as in the third law of mathematical principles of TCNP. The same curve can also be viewed as the spectral characteristics of impinging radiation on the metal surface. To explain the normal and selective photoelectric effects, all we have to do is to put one curve on top of the other and slide the former over the latter from the left to right. It is clear that the energy of the photo electricity will depend on how much the frequency (not the intensity) of radiation is overlapped with the pass band. Combining these results, it shows that the emission and absorption of radiation can be explained very well by the undulatory theory of TCNP. Since we know already that the transmission of radiation and light have to be explained in terms of waves, we can claim that the theory of optics, from generation, transmission to absorption can be unified successfully using CWTFC without invoking the quantum theory at all. To give a brief summary here, it can be seen from the previous discussions that the spontaneous emission of blackbody radiation can be modeled as undulatory waves in CWTFC with 0 < H < 0.5 and the spiking phenomena in maser and laser dynamics can be explained under undulatory theory in CWTFC with 0.5 < H < 1. CWTFC has also been used to explain the selective effects in photo-electricity. Hence, the theory of optics can be explained by the model of CWTFC without invoking the photon theory or quantum optics at all. It is believed that other phase transition problems in modern physics and physiology can also be explained by using similar derivations of this review paper. For instance, the urine storage and micturition problems in the lower urinary tract of TCM physiology can also be explained from the perspective of phase transition. Consequently, TCM can be unified under the same mathematical principles of TCNP.

The cosmology and ontology of TCNP was denoted by terse concepts such as Qi, Yin-Yang and Five-Phases. These terms were used by ancient sages to describe the world around them. In modern representation, these concepts have been characterized as the CWTFC. In order to have operational meanings, three basic laws of mathematical principles in TCNP have been proposed for later applications. Based on these laws, the physiology, pathology, diagnostics, and treatments of TCM can be built on a solid foundation. Moreover, using the same set of laws, sciences in terms of the TCNP has been proposed and proven to be much closer to reality when compared with their Western counterparts. Some of the applications presented in this review paper have included acupuncture, Chinese herbology, astronomy, blackbody radiation, generalized uncertainty principle, and laser. It is now fitting to conclude that the TCM, TCNP and its sciences have been unified as a grand system and hopefully it can become an ecumenical one in the future.

In this section, before giving the final accurate answer to NGQ, let us once more examine the four great inventions of ancient Chinese sciences and civilization that have been so much more efficient than the European West in applying human knowledge of Nature to useful purposes. The first of these four is nautical compass. The theory behind nautical compass is geomagnetism. The earliest reference to magnetism in Chinese literature can be traced back to the 4^nd century B.C. in the book of the Guiguzi: “The lodestone makes iron come, or it attracts it”. According to Needham, the Chinese in the Song Dynasty and continuing Yuan Dynasty already knew how to make use of a dry compass. In order to invent nautical compass, the inventors had to know somehow the existence of a geomagnetic field of the earth. It is fair to say, even nowadays, the real mechanism of this celestial phenomenon still cannot be explained and validated in terms of microscopic electron spin theory. In any case, the geomagnetism behind nautical compass must be based on a global field effect of TCNP.

The second of four great inventions is gunpowder. Gunpowder was invented in the 9^th century by alchemists searching for elixir of immortality. In the Song Dynasty, various formulas for gunpowder held levels of nitrate were recorded. Incidentally, the first “fire-crackers” were actually the joints of bamboo thrown on a fire; the noise from such explosion is huge. During that time, the theory of explosion or detonation was not clearly understood. However, the physical and chemical reactions took place have to do with propagation of shock waves. At that time, although people cannot distinguish if the shocks were either linear or nonlinear waves, however the Chinese must know from their TCNP that it must be some kind of waves. It is based on this kind of understanding can people start doing research on how to improve the power of gunpowder.

The third of four great inventions is papermaking. Papermaking could be traced back to China about 1st century A. D. when Cai Lun produced a sheet of paper using mulberry, bast fibers and hemp. If one studied the processes of papermaking, one should be able to see that the materials had to consist of continua of fibers being processed repeatedly several times that were self-similar with fractal structure. This theory is in conformability with our CWTFC and TCNP.

The fourth of four great inventions is printing of movable types. The development of this printing type enabled ancestral knowledge of human beings to be stored and passed to later generations with much greater fidelity. In addition to the four great inventions, let us consider the following important achievements in astronomy. It is noteworthy that many ancient civilizations had collected astronomical information for a long period of time through observation. However, it is the Chinese astronomy that was more complete in a systematic manner. Though the real physical structure of planets and stars were not comprehended, however, various theories were proposed. By examining the data collected for more than a few thousand years, the contribution of Chinese astronomy can be described as a great achievement in providing real data for celestial chaotic motions. Astronomical observations from China constitute the longest continuous sequence from any civilization and include records of sunspots (112 records from 364 BC), supernovas (1054), lunar and solar eclipses. By the 12th century, they could reasonably accurately make predictions of eclipses, but the knowledge of this was lost during the Ming dynasty, so that the Jesuit Matteo Ricci gained much favor in 1601 by his predictions. By 635 Chinese astronomers had observed that the tails of comets always point away from the sun.

It is noteworthy that Needham in his book (Needham, 1959) mentioned that (a) the interest in Nature, such as astronomy, was not enough, (b) having controlled experimentation was not enough, (c) empirical induction was not enough, (d) eclipse prediction and calendar calculation were not enough for Chinese to mathematize natural science. He contended that “a mercantile culture alone was able to do what agrarian bureaucratic civilization could not bring to fusion point the formerly separated disciplines of mathematics and nature knowledge” (Needham, 1969). Apparently, this viewpoint is not very convincing as an accurate answer to NGQ.

Let us now give the accurate answer to NGQ. The first part of NGQ will be discussed first. It was on the reason why between the 2^nd century B.C. and the 16^th century A.D., East Asian culture was much more efficient than the European West in applying human knowledge of Nature to useful purposes. The accurate answer to this part of the grand question is that, according to our descriptions at the beginning of this section on the ancient Chinese scientific achievements, the wave or field concepts in TCNP are conformable and more in line with Nature so they are more efficient in applying human knowledge to useful purposes. It was pretty efficient without outside challenges for the first 18 centuries. As to the second part of NGQ, the reason why modern science did not take its meteoric rise in China at the time of Galileo is simply because the reductionist viewpoints of modern sciences are not conformable to Chinese natural philosophy and they are not flawless. Hence, it did not take its meteoric rise in China. In addition, the mathematics at that time was not sophisticated enough for the fusion of mathematics and nature knowledge. We have to wait for the time, until only recently, that the mathematical tools are available so as to deal with the complex dynamic problems. In the Introduction section, it was mentioned that Needham actually insightfully made an interesting remark that the “Chinese physical world view is wave instead of atom and continuum instead of discontinuity”. As a result, the interaction from the Western physical world view needs collision of atoms and molecules, yet the approach from the Chinese physical world view would be more of a field or wave approach. Unfortunately, he did not go any further to probe into the wave theory of continuum so as to find out the accurate answer. Using the mathematical principles of CWTFC in the previous sections, we are able to illustrate that the TCM, TCNP and its applications in sciences are much closer to reality than its modern Western counterparts. So, it is the field or wave approach that can explain why Chinese culture was much more efficient than the European West in applying human knowledge of Nature to useful purposes for the first 18 centuries. It is believed that the hallmarks of fractal continuum in the structure and chaotic wave in the interactions will be able to continue the successes that have stopped only for the recent three centuries.

In this review paper, the accurate answer to NGQ has been reviewed and sought. Some of the answers have been sought from the domains outside of science and technology per se. However, this question was posed in the context of science and technology at the outset and an accurate answer within the scientific disciplines has been found.

It is well-known that the holistic approaches of TCM, TCNP and its sciences have been very successful for the first eighteen centuries. They have been stagnant only in the recent three centuries. The main obstacle in preventing the advancement of TCM, TCNP and its sciences is actually the lacking of proper mathematical tools in dealing with such complex dynamical systems. Fortunately, the time is now ripe and the proposed CWTFC and its three laws can be used to unify TCNP and TCM. It is believed that the ancient scientific and medical achievements can now be resumed and continued. This new theory, hopefully, will be able to help promoting the genuine understanding of natural philosophy, natural sciences, and medicine in an ecumenical way.