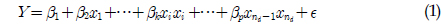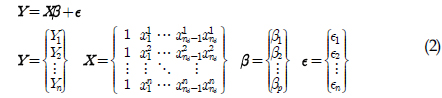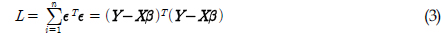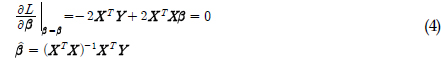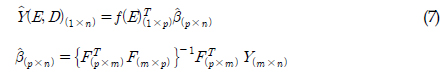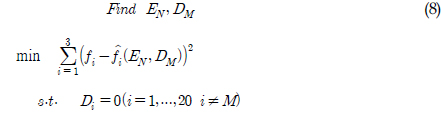해양 플랜트 구조물은 해양 석유 탐사 및 개발, 해양 온도차 발전, 심해저 광물자원 개발 등 다양한 해양개발 분야에서 매우 중요하게 사용되고 있다. 최근 해양 석유 탐사/개발 영역이 점점 깊은 수심으로 이동하고 있으며, 심해저 광물자원 개발의 연구가 진행됨에 따라, 심해용 해양 플랜트 구조물 기술이 매우 중요하게 인식되고 있다. 이러한 해양 플랜트 구조물은 혹독한 해양환경(파도, 조류, 해풍, 수압, 와류진동, 염분 등)에 장기간 노출된 상태로 운용되기 때문에 구조가 손상될 가능성이 높고, 해양에 위치한 특성상 구조에 손상이 발생될 경우 인명피해 및 경제피해가 매우 크게 발생될 수 있다. 특히 2010년 4월 멕시코만에서 발생한 Macondo 사고 이후 해양구조물의 안전성에 대한 관심이 크게 고조되고 있으며, 구조물, 기기 및 배관의 건전성 감시를 위한 연구의 필요성이 대두되고 있다.
구조물의 물리적 특성 변화는 외적 자극에 대한 응답의 변화를 초래한다는 기본개념에 기초한 구조건전성 모니터링(SHM, Structural health monitoring)기법은 1970년 대 후반 수행된 해양구조물에 대한 선구적 연구(Vandiver, 1975)를 시작으로 지난 40년간 활발한 연구가 진행되어 왔다. 현재까지 여러 가지 이론에 기반을 둔 많은 기법이 개발되어 교량, 건물 등 주요 기반시설물에 적용되고 있는 상태이다. 이러한 구조 건전성 모니터링 기법들은 주로 정적 또는 동적응답을 이용하고 있으며, 구조물의 지속적인 감시가 가능하다는 측면에서 동적응답에 기반을 둔 기법들이 선호되어 왔다. 현재까지 개발된 동적응답 변화에 기반을 둔 구조 건전성 모니터링 기법들은 주로 가속도, 속도, 변위, 변형률 등 구조물의 동적응답 측정기법, 계측된 응답을 이용한 후처리를 통한 목적응답 추출기법, 목적응답의 변화를 이용한 유효물성치 산정기법 및 손상탐지 기법과 같은 다양한 탐지기법의 조합으로 구성되어 있다.
Kim et al.(2000)은 소수의 진동모드 특성치와 패턴인식 알고리즘을 이용한 손상추정 기법을 제시하였으며, Lee et al.(2009)은 최적화 화음탐색법을 이용해 항만 케이슨 구조물의 구조건전성을 평가하였다. Park et al.(2011)은 고유주파수와 모드형상을 이용해 자켓구조물의 손상을 추정하였다. Min et al.(2011)은 조류발전 구조물의 장기 건전성 모니터링을 위하여 전기-역학적 임피던스 기반 모니터링 기법을 연구하였다. Min et al.(2012)은 고유진동수와 제로진동수를 이용한 보 구조물 손상추정 연구를 수행하였다. Kim et al.(2012)은 해상풍력발전기 지지구조물 손상추정을 위하여 신경망기법을 이용하는 연구를 수행하였다. 이외에도 많은 연구가 국내외에서 수행되었음에도 불구하고 아직까지 해결되지 못한 문제들이 있다. 우선, 이러한 연구들은 손상전 모델과 손상후 모델의 고유주파수, 모드형상 등과 같은 진동특성 비교를 통해 손상의 크기와 위치를 추정하기 때문에 초기 구조물의 진동특성이 계측된 경우에만 손상추정이 가능한 단점이 있다. 또한, 유한요소 모델과 같은 모델링을 통한 해석 수행이 반복적으로 진행되기 때문에 현장 시설 운용자들이 사용하기에는 매우 복잡한 해석절차를 가지는 어려움이 있다.
이러한 단점을 극복하기 위하여, 본 연구에서는 메타모델(Meta model)을 사용한 손상추정 기법을 제시하고자 한다. 메타모델은 긴 해석시간이 요구되는 시뮬레이션 모델을 최적설계에 적용하기 위해 개발되었으며 통계적 기법을 통해 시뮬레이션 모델의 응답을 예측하는 기법이다. Faravelli and Casciati(2004)와 Casciati(2010)은 구조물의 손상 여부를 판별하고 손상 위치를 추정하기 위하여 반응표면모델(response surface model)을 적용한 손상추정 기법을 연구하였다. 두 연구에서는 측정된 가속도 신호를 이용하여 손상을 판별하고 손상 위치를 추정하는 방법을 제시하였으나, 손상의 크기를 판별할 수 있는 방안은 제시하지 못하였다.
본 연구에서는 손상 위치 및 손상 크기를 추정할 수 있는 메타모델 기반 손상추정 기법을 제시하고자 한다. 유한요소 모델을 현장에서 반복적으로 해석할 필요 없이 미리 각 요소의 손상정도에 따라 유한요소모델을 해석하여 응답 데이터를 미리 추출, 정확한 메타모델을 생성하고 임의의 응답 데이터가 획득되었을 때 그 응답 정보에 대한 메타모델 상에서의 설계변수, 즉 손상 부재 및 손상도를 추정하는 방법을 제안한다. 외팔보와 2차원 자켓구조를 대상으로 손상 시나리오를 작성하여 제시된 기법의 효용성을 검증하였다.
메타모델 기법은 설계변수와 응답함수 사이의 관계를 통계적인 기법을 이용하여 간단한 수학 모델을 만드는 기법이다(Morris and Mitchell, 1995). 이러한 메타모델은 최적설계 과정에서 반복적으로 수행되는 계산비용이 큰 해석모델을 대체하여 최적설계 과정의 시간과 비용을 줄이는 효과를 얻기 위해 연구되었다. 메타모델을 적용하게 되면 해석모델은 설계변수와 응답에 대한 메타모델을 구성할 때만 사용되고 최적설계 알고리듬은 구해진 메타모델과 연동하게 된다. 메타모델은 주어진 입력에 대해서 응답의 실시간 평가가 가능하기 때문에 최적설계 과정의 추가적인 수치적 비용이 필요하지 않다. 특히 메타모델링 기법은 계산비용이 많이 드는 시뮬레이션모델의 해석과 최적설계 과정이 분리됨으로써 설계자가 보다 다양한 설계정식화를 시도하여 시스템에 대한 설계정보를 얻는 설계도구로도 활용될 수 있다는 장점이 있다. 메타모델은 모집단(Population)인 모사모델(Simulation model)에서 실험계획(Design of experiment, DOE)을 통해 표본(Sample)을 추출하고, 표본자료(Sample data)의 통계적 추정(Statistical estimation)을 통해 메타모델을 구성한다. 메타모델은 특성에 따라 크게 회귀모델과 보간모델로 분류된다. 회귀모델은 사전지식(Prior knowledge)에 따라 임의의 수학적 모형을 가정하고, 이 모형을 표본으로부터 추정하는 통계적 분석방법이며 보간모델은 표본의 정보를 중심으로 모집단의 정보를 추정하는 형태로 구성된다. 따라서 회귀모델은 모든 표본을 정확하게 표현하는 보간모델에 비해 현재 표본들을 정확하게 표현하지는 못하지만 경향성을 확인하는데 적합하며, 강건한 모델을 생성할 수 있다는 장점이 있다. 또한 국부 변화가 심하지 않은 선형적인 경향을 보이는 응답에 대해서 정확한 해를 제공한다는 장점이 있다. 구조물의 손상 추정에 사용되는 응답들은 고유진동수, 고유모드와 같이 사전지식이 존재하고 국부적 비선형성이 크지 않다는 점에서 본 연구에서 메타모델은 대표적 회귀모델인 반응표면모델을 사용하였다(Montgomery, 2007). 반응표면모델은 설계변수와 응답함수 사이의 관계를 다음과 같이 다항식의 형태로 나타낼 수 있다고 가정한다.
여기서
반응표면모델과 데이터의 오차제곱합은 다음과 같이 표현할 수 있다.
최소제곱법은 오차제곱합을 최소로 하는
이 추정계수를 이용하여 다음과 같은 반응표면모델을 얻을 수 있다.
여기서
일반적으로 반응표면모델은 계수의 개수보다 더 많은 샘플점들을 사용하기 때문에 추정된 모델은 데이터를 지나지 않는 회귀모델이 된다. 또한 반응표면모델은 계수를 추정하는 과정이 단순한 역행렬 계산만을 요구하기 때문에 크리깅에 비해 구현이 간단하다. 한편 방사형기저함수와 같이 기저함수의 폭을 정해주어야 하는 모수(Parameter)가 없지만 설계변수와 응답의 다항식 관계를 어떻게 설정하는가가 반응표면모델의 정확성에 중요한 인자이다.
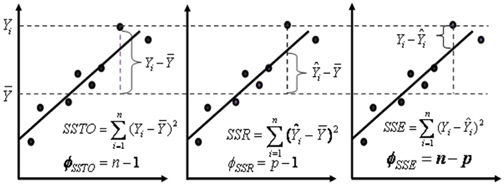
반응표면모델을 생성하면 구해진 반응표면모델이 실제 데이터의 변화 특성을 얼마나 잘 반영하고 있는지 검증이 가능하다. 이것은 총 변동(Total sum of squares, SSTO)에 대한 반응표면모델이 설명할 수 있는 변동(Regression sum of squares, SSR)의 비(Ratio)를 이용하여 평가할 수 있다.
SSTO는 평균으로부터 각 데이터까지의 변동에 대한 제곱합이고, SSR은 이러한 변동 중에서 반응표면모델에 의해 설명될 수 있는 변동 에 대한 제곱합으로 Fig. 1에서 확인할 수 있다. 따라서 구성된 반응표면모델이 정확하다는 것은 SSR이 SSTO에 가까워 오차제곱합(SSE)가 매우 작게 되는 것을 의미한다. 이러한 SSR에 대한 SSTO의 비가 결정계수(Coefficient of determinant)이며, 반응표면모델이 정확할수록 1에 가까운 값을 갖고, 모델의 정확성이 떨어질수록 0에 가까운 값을 갖는다.
본 장에서는 메타모델의 장점을 활용하여 구조물의 손상 추정을 위한 새로운 기법을 제시하고자 한다. 구조물의 손상추정을 위해서는 공간-손상 변화를 동시에 고려할 수 있는 통계적 메타모델 생성이 필요하다. 즉 구조물이 위치하는 공간 변화에대해서 응답이 예측되어야 하며 이와 더불어 각 위치의 손상 정도에 대해서도 응답이 예측될 수 있어야 한다. 그래야만 특정 응답에 대한 공간 위치와 손상 정도를 제공할 수 있기 때문이다. 하지만 공간-손상 변화를 동시에 변수로 취급하여 하나의 메타모델로 생성할 경우 실험점이 많이 필요하다는 문제와 전혀 다른 성향의 공간변수와 손상변수를 동시에 취급함에 따라 불필요한 교호작용의 발생 등의 문제가 존재한다. 이는 공간-시간 변화에 대한 접근법과 유사하다는 특징이 있다. 공간변수와 시간변수 역시 다른 특징을 지니고 있으며 공간-시간변수를 동시에 고려할 경우 문제가 발생하는 부분에 대해 많은 연구가 이루어졌다. 이 중 Lee and Lee(2010)가 제안한 다중응답접근법(Multiple response approach)은 공간변수만 메타모델을 구성하는 변수로 고려하고 각 시간점(Time point)에서의 응답들은 다중응답으로 고려하여 시간점 개수만큼의 메타모델을 구성하여 효율적으로 시간변수를 고려할 수 있는 기법으로 알려져 있다. 본 연구에서는 공간변수보다 손상변수가 비선형성이 적기 때문에 손상변수에 대한 메타모델을 구성하고 각 공간에 대한 각각의 메타모델을 다중응답 형태로 고려하는 새로운 개념의 손상추정 기법을 제안한다.
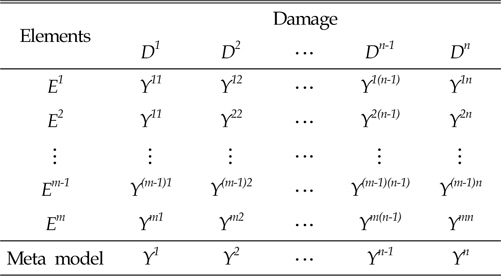
Table 1은 공간변수에 대한 다중응답을 나타낸다. 손상변수에 대한 실험점
[Table 1] Multiple responses for element numbers
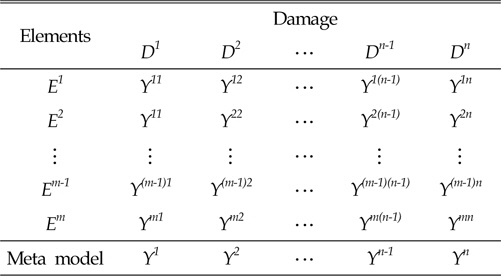
Multiple responses for element numbers
여기서, 아래 첨자는 행렬의 차원을 나타낸다
다중응답접근법 기반 통계적 공간-손상 메타모델은 공간변수를 메타모델을 구성하는 변수가 아닌 다중응답으로 고려하기 때문에 공간변수인 요소개수가 늘어나더라도 메타모델이 많아지지 메타모델을 구성하는 설계변수가 늘어나는 문제는 나타나지 않는다. 이는 향후 복잡한 구조물의 손상위치 및 정도를 추정할 때 제안된 기법의 장점이 될 수 있을 것으로 판단된다.
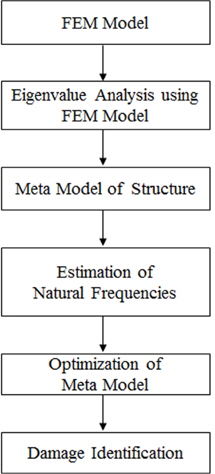
이제 구조물의 손상을 추정하기 위하여 요소-손상에 대한 고유진동수 메타모델(즉, 요소 위치와 강성 변화에 따른 고유진동수 변화를 수식적으로 표현하는 모델)을 이용하는 방법을 Fig. 2와 같이 구성하였다. 우선, 구조물 제작에 사용된 최종 설계도를 기반으로 유한요소 모델을 생성한다. 생성된 유한요소 모델의 각 요소위치에 대한 강성변화를 미리 구성한 손상 시나리오에 따라 다양하게 변경해가며 고유치 해석을 반복하여 수행한다. 반복 해석을 통해 획득된 고유진동수 데이터를 이용하여 각 요소에 대한 요소-손상에 대한 고유진동수 메타모델을 생성한다. 다음으로, 실제 구조물에 부착된 센서를 통해 응답신호를 획득하고, 획득된 신호를 분석하여 구조물의 고유진동수를 계측한다. 이 단계에서 계측된 고유진동수, EXP(
제안된 손상추정기법을 검증하기 위하여 원형 외팔보 모델을 Fig. 3과 같이 생성하였다. 수치해석 모델에 사용된 물성치와 수치는 Table 2와 같다. 총 20개의 요소와 21개의 절점으로 구성되었으며, 각 절점 당 2개의 자유도(회전과 병진 자유도)를 가지고 있다.
[Table 2] Properties of a FE model

Properties of a FE model
본 연구에서는 요소의
[Table 3] Damage scenarios of the FE model

Damage scenarios of the FE model
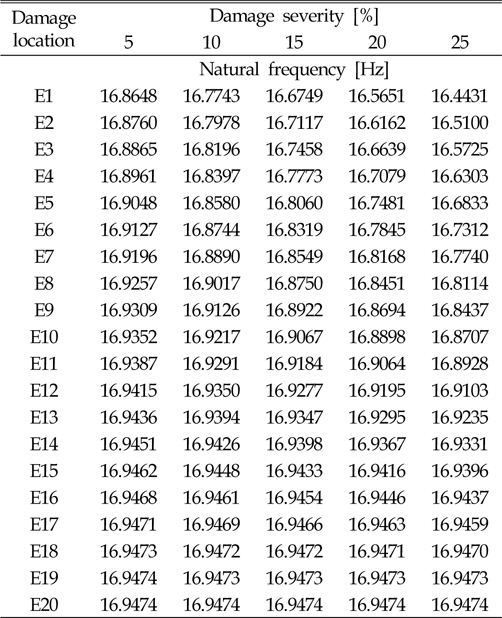
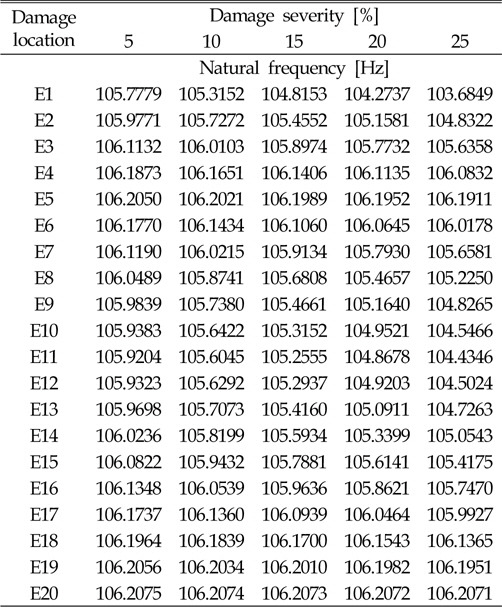
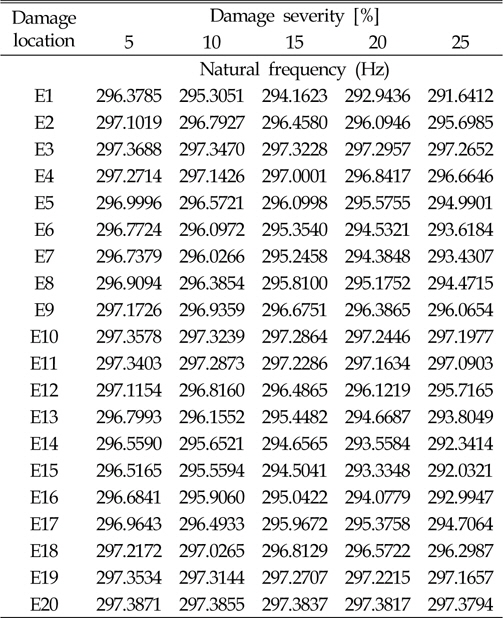
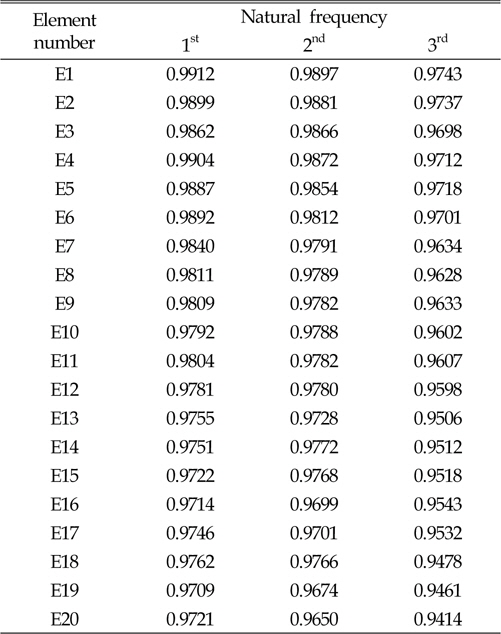
본 연구에서는 설계변수와 응답함수 사이의 관계를 다항식의 형태로 나타내는 반응표면모델을 사용하였다(Lee et al., 2006). 고유진동수는 재료의 강성변화의 제곱근에 비례하기 때문에 비선형성이 크지 않아 적용 및 검증이 용이한 반응표면모델을 적합모델로 선정하였다. 반응표면모델은 각 요소마다 개별적으로 생성이 되어 요소 개수만큼의 반응표면모델이 손상추정에 사용된다. 따라서 본 연구에 사용된 모델은 1개 요소의 손상을 추정할 수 있으며 요소간의 교호작용은 고려하지 않는다. 손상위치와 고유진동수 변화관계 메타모델을 생성하기 위하여 각 요소마다 손상정도를 5%, 10%, 15%, 20%, 25%로 변경하며 1~3차 고유진동수를 계산하였으며, Table 4~6에 각각 정리하였다. 생성된 모델의 정확도는 Table 7과 같이 94% 이상으로 정확한 모델임을 확인하였다.
[Table 4] First natural frequencies at different damage location and damage severity
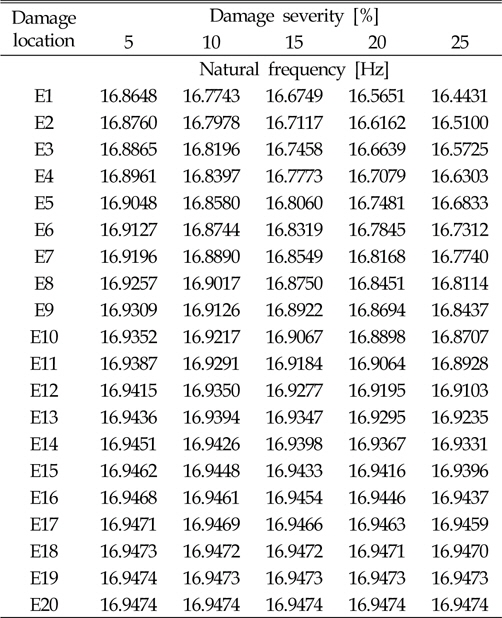
First natural frequencies at different damage location and damage severity
[Table 5] Second natural frequencies at different damage location and damage severity
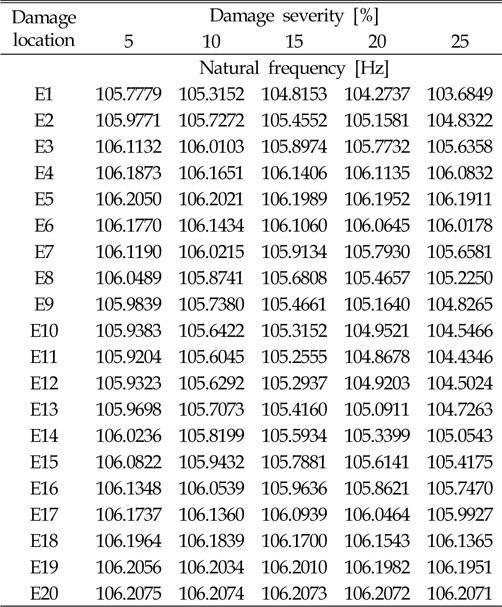
Second natural frequencies at different damage location and damage severity
[Table 6] Third natural frequencies at different damage location and damage severity
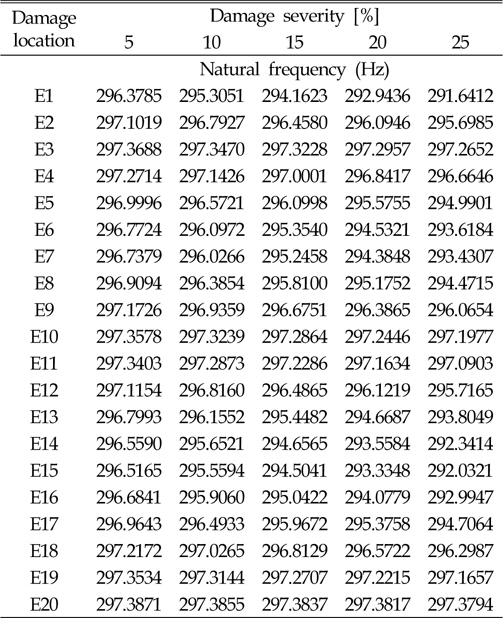
Third natural frequencies at different damage location and damage severity
[Table 7] R2 of response surface model(RSM)
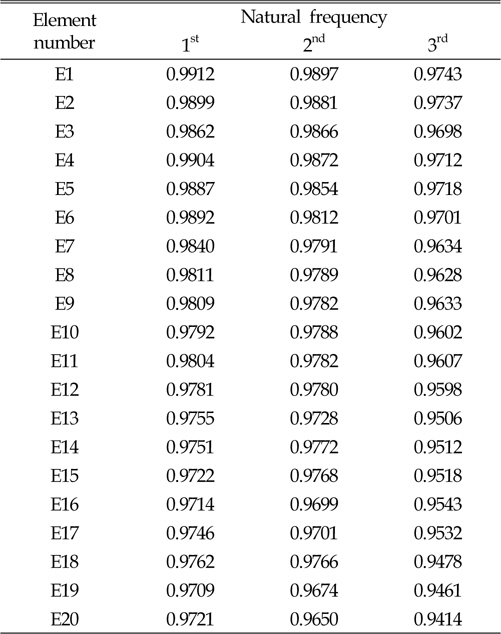
R2 of response surface model(RSM)
손상 위치 및 손상도를 추정하기 위해 다음과 같이 설계 정식화를 수행하였다.
여기에서
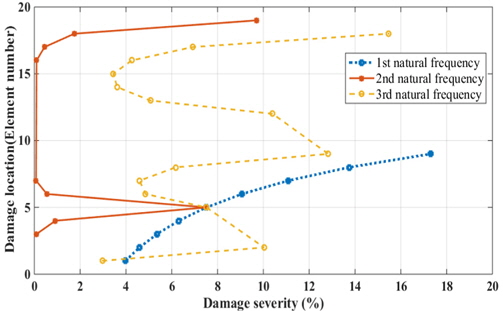
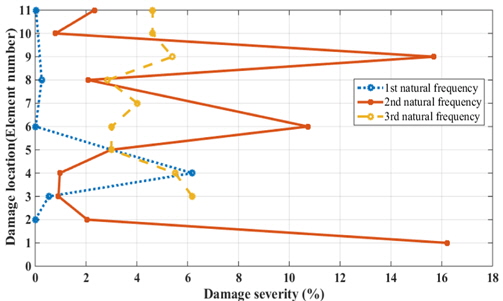
제안된 손상추정 기법의 정확도를 알아보기 위해 두 개의 손상 모델에 대한 1~3차 고유진동수를 추출하여 손상 부재 및 손상도를 추정하였다. 두 개의 손상 모델에 대한 정보 및 추정 결과는 Table 8과 같으며 각 손상 모델의 추정 결과는 Fig. 4와 Fig. 5에 나타냈다. Fig. 4와 Fig. 5는 제공된 손상 모델의 각 고유진동수(
[Table 8] Information of two damage models and predicted damage information from RSM models

Information of two damage models and predicted damage information from RSM models
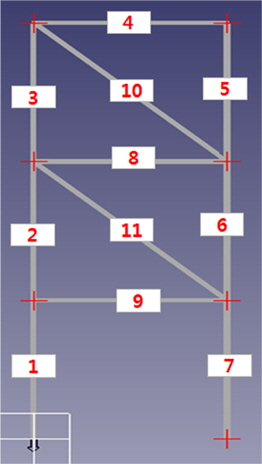
보요소 11개로 구성된 2차원 자켓 구조물을 상용 소프트웨어인 DAFUL 5.0을 사용하여 Fig. 6과 같이 모델링 하였다. 수평부재(4번, 8번, 9번 요소)와 수직 부재(1번, 2번, 3번, 5번, 6번, 7번 요소)의 길이는 모두 1m이며, 1번 요소와 7번 요소의 지지점은 모두 고정된 상태이다. 수치해석 모델에 사용된 요소의 물성치와 수치는 Table 9와 같다.
[Table 9] Properties of a FE model

Properties of a FE model
이번 수치 모델에서도 요소의
[Table 10] Damage scenarios of the FE model

Damage scenarios of the FE model
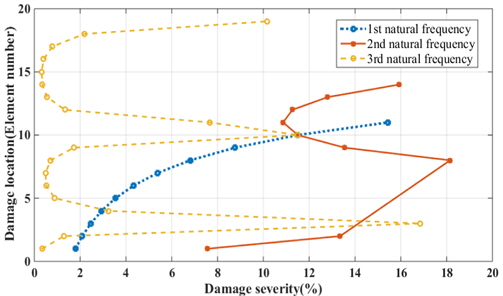
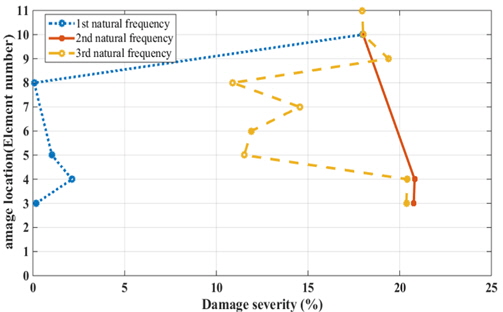
각 요소마다 손상정도를 5%, 10%, 15%, 20%로 변경하며 1~3차 고유진동수를 계산하였다. 계산된 고유진동수 데이터를 이용하여 손상위치와 고유진동수 변화관계 메타모델을 획득하였으며, 식 (8)을 통해 2차원 자켓 구조물의 손상을 추정하였다. Case 3과 Case 4의 손상 모델에 대한 추정 결과와 정확도는 Table 11과 같다. Fig. 7과 Fig. 8은 제공된 손상 모델의 각 고유진동수(
[Table 11] Information of two damage models and predicted damage information from RSM models

Information of two damage models and predicted damage information from RSM models
본 연구에서는 해양플랜트 구조물의 손상추정을 위해 메타 모델을 이용하는 기법을 제안하였으며, 제안된 기법을 외팔보와 2차원 자켓 구조물 수치 손상 모델을 통해 검증하였다. 그 결과 다음과 같은 결론을 얻을 수 있었다.
(1) 메타모델을 이용할 경우 신호 계측 이외의 추가적인 해석절차가 필요하지 않았다. 이러한 장점은 현장 관리자들의 사용편의성을 극대화 할 수 있을 것으로 생각된다. (2) 구조물 제작과 동시에 수치모델을 이용한 손상위치-손상정도에 대한 고유진동수 변화 데이터베이스를 작성하면, 구조물 유지/관리를 위한 시스템 제공이 가능할 것으로 생각된다. (3) 손상위치를 탐색하기 위한 최적설계 진행 시 시뮬레이션 모델이 직접 사용되지 않고 실시간으로 응답이 도출되는 메타모델이 시뮬레이션 모델을 대체함으로써 계산 비용을 감소시킬 수 있으며, 실시간 모니터링이 가능할 것으로 판단된다. (4) 각 고유진동수의 진동 모드가 다르기 때문에 한 개의 손상에 대한 반응표면모델 예측은 단일 해를 가지며 제시한 두 개의 손상모델에 대해 손상위치를 정확히 탐색하였으며 손상정도는 0.27% 이내의 정확도로 추정하였다.
하지만 제한된 기법을 실제 해양플랜트 구조물에 적용하기 위해서는 다음과 같은 사항들을 고려하여야 한다.
(1) 다중 손상점에 대한 메타모델 생성 기법이 연구되어야 한다. 이를 위해서 요소간의 교호작용이 고려된 메타모델 생성기법이 필요하며 다중 솔루션에 대한 처리기법이 필요하다. (2) 고유진동수 이외의 응답 데이터(모드형상, 스트레인 등)를 이용한 메타모델 기법도 추가로 연구되어야 한다.
위의 사항들을 고려하여 해양플랜트 구조물에 적용 가능한 손상추정기법을 향후 개발하고자 한다.