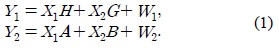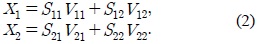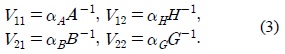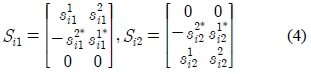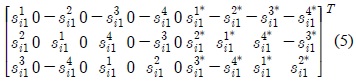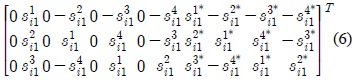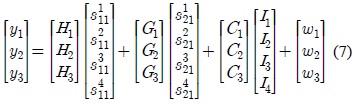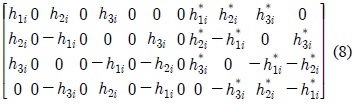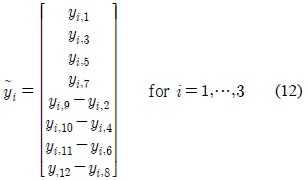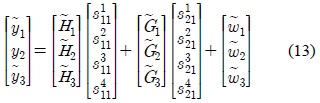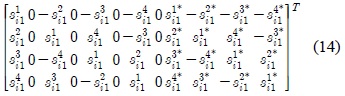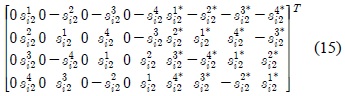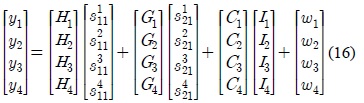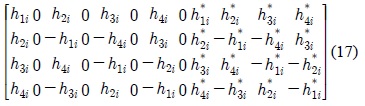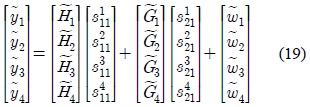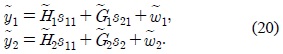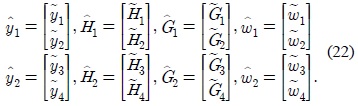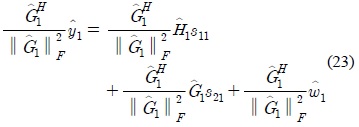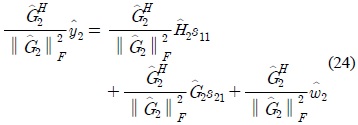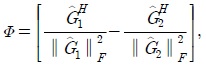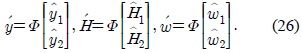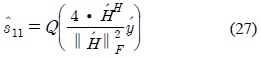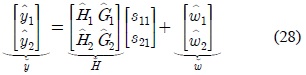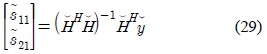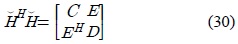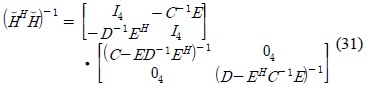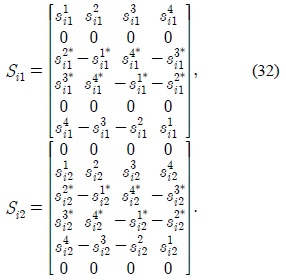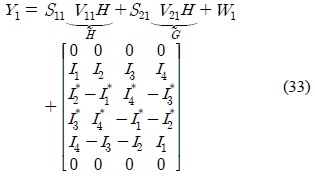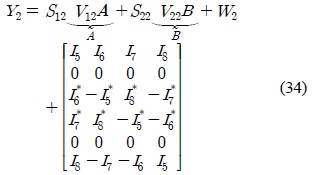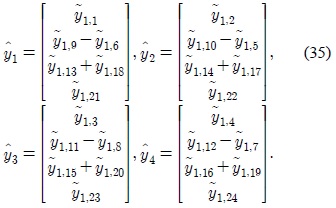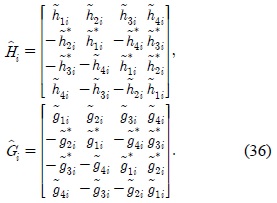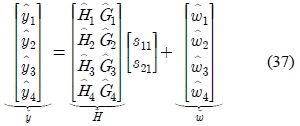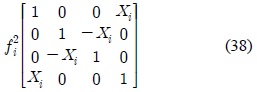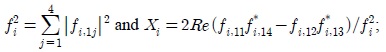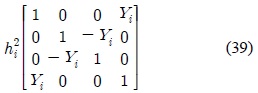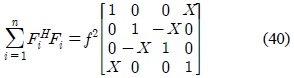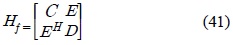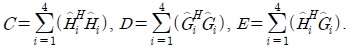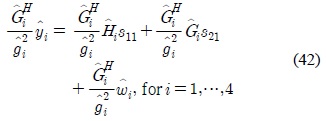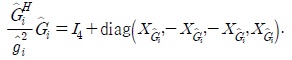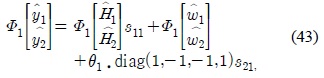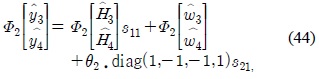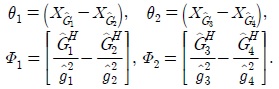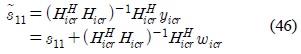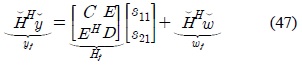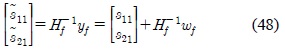In wireless communications systems, interference plays a major role in defining the achievable performance and capacity [1,2]. In conventional receivers, in multi-user scenarios, the interference is either ignored, hence considered as an additional noise, or jointly decoded via employing successive interference cancellation (SIC) detectors [3-5]. In both cases, the dimension of the interference remains the same, leading to degraded performance and diversity gain in the first case, while powerful algorithms should be employed in the case of SIC so as to avoid degradation in the performance.

Interference alignment is a transmission technique used to reduce the dimensions of the interference while maintaining the useful signals discernible at the intended receivers. This is achievable by precoding the transmit signals such that the interference is aligned at unintended receivers [6]. As such, interference is removed at the intended receivers using simple mathematical operations leading to an interference-free system, where appropriate decoding algorithms can then be used to decode the useful signals. In [6], Jafar and Shamai proposed a linear alignment algorithm for the two-user X channel, that achieves the maximum data rate of (4/3 × n_T) symbols/channel use and a diversity gain of 1, with n_T denoting the number of antennas at each terminal.

In addition to the multiplexing gain, quantified by symbols/channel use, the diversity gain is an important measure of the system performance. When the channel is in deep fading, systems with unity diversity gain suffer from low signal-to-noise ratio (SNR) at the receiver side, leading to degradation in the bit-error rate (BER). Several diversity techniques have been proposed in the literature to explore further diversity gain [7-9]. In [10], a technique that combines interference alignment in X channel and Alamouti diversity scheme with two transmit antennas has been proposed to achieve the maximum multiplexing gain of (n_T × 4/3 = 8/3) and the full diversity gain of 2, which is equal to the number of antennas at each of the four nodes. Furthermore, the proposed scheme inherits the space-time orthogonality of the Alamouti algorithm, hence a simple linear receiver, that avoids computationally complex matrix inversion, is required to achieve the aforementioned gains.

In this paper, we propose several transmitter and receiver structures for the case of more than 2 transmit antennas aiming to increase the diversity and power gains. First, we examine the combination of orthogonal space-time block codes (OSTBC) for n_T = 3 and 4 with code rate R_c = 1/2 built on the 2-user X channel system with interference alignment. Due to the orthogonality of the codes, a modified interference cancellation receiver (ICR) is used to decouple the symbols transmitted from the two transmitters. Surprisingly enough, due to the special structure of the effective channel matrices, we show that the simple linear zero-forcing(ZF) receiver achieves the full diversity without requiring explicit matrix inversion. We extend this scenario to the quasi-orthogonal STBCs (quasi-OSTBCs) with n_T = 4, where in addition to proposing the interference alignment structure, we introduce a modified version of the ICR that takes into consideration the non-orthogonal nature of the codes. Note that the extension to the case of n_T = 2⁽ⁿ⁺²⁾ for any positive integer n is possible. Furthermore, we show once again that the simple ZF receiver is superior to the ICR in terms of power and diversity gains. Due to the non-orthogonality of the effective channel matrices, the achieved diversity in this later case slightly lacks the optimum value. Further research will be conducted to detail the reasons behind such a degradation and investigate methods to minimize it. It is fundamental to mention that in this paper we don't claim that our proposed techniques achieve the maximum multiplexing gain of (n_T × 4/3). However, at the same spectrum efficiency, quantified by bits/Hz/channel use, our proposed schemes achieve far better performance in terms of power and diversity gains.

The rest of the paper is as follows. In Section II we introduce the system model and review the LJJ scheme. In Sections III and IV, we introduce the OSTBCs and quasi-OSTBCs built on the 2-user X channel with interference alignment, respectively. In Section V we present the simulation results and in Section VI we draw the final conclusions.

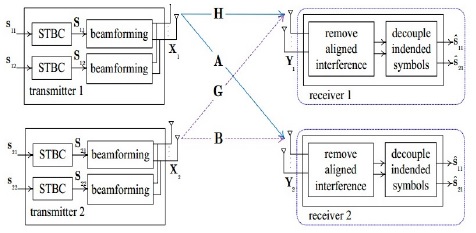
Consider a two-user X channel system as depicted in Figure 1, with each of the two transmitters equipped with n_R antennas and each of the receivers equipped with antennas, where in the deployed scenario n_T = n_R. Each transmitter has independent symbols intended for each of the receivers. These symbols are drawn independently from a finite modulation set Ω. Transmitter 1 has intended for receiver 1 and receiver 2, respectively. In , the superscript k denotes the index of the symbol, the first subscript denotes the index of the transmitter, and the second subscript denotes the index of the intended receiver. Likewise, transmitter 2 has intended for receiver 1 and receiver 2, respectively. Vectors s_ij , for i,j = 1,2 are encoded by the STBC block to generate the T × n_T matrices s_ij, for i,j = 1,2, with T denoting the number of channel uses. Finally, encoded symbols are beamformed and linearly combined to generate the T × n_T block codes X_i, for i = 1,2. To denote the channels between the transmitters’ and the receivers’ antennas, we use H, G, A and B to denote the n_T × n_R matrices coupling transmitter 1 and receiver 1, transmitter 2 and receiver 1, transmitter 1 and receiver 2, transmitter 2 and receiver 2, respectively. Each entry in the channel matrices is i.i.d.CN(0,1), where CN(μ,σ²) denotes a complex Gaussian random variable with mean and variance of μ and σ². The T × n_T signal matrices received at the antennas of receiver 1 and receiver 2, respectively, are given by:

The elements of the noise matrices W₁ and W₂ are i.i.d.. The block codes are given as following:

The beamforming matrices V_ij for i,j = 1,2 are designed to align the interference at the unintended receivers. That is, are aligned at receiver 2, whereas are aligned at receiver 1. The zero-forcing precoding is a suitable choice to design the beamforming matrices V_ij for i,j = 1,2. As such, they are given by:

where the real-valued scalars α_A, α_H, α_B, and α_G satisfy the power constraint , where tr(•) denotes the transpose operator. Hence, for any matrix R.

In the LJJ scheme [10], each node is equipped with 2 antennas where each transmitter has K = 2 symbols intended for each of the two receivers. As such, at each channel use a total of 4 × K = 8 symbols are transmitted. These symbols are encoded using Alamouti scheme as following:

for i = 1, 2, where i refers to the index of the transmitter. Note that the conjugated symbols are present in the same row of S_i1 and S_i2. At the receivers, the corresponding rows in the receive block codes are conjugated so that the system can be re-written as a function of conjugate-free symbols. The details of the decoding process which is partially similar to that depicted in [10].

It is proven that Alamouti scheme is the only OSTBC with rate R_c = 1. For more than 2 transmit antennas, several orthogonal codes have been derived with lower rates (i.e., R_c < 1). In the following section, we investigate the integration of OSTBC with R_c < 1 in the system depicted in Figure 1. Our goal is to increase the diversity gain [12], while maintaining the same capacity, quantified by bits/channel use, as compared to the LJJ algorithm.

For the case of n_T = 3, the matrices S_i1 and S_i2 for i = 1,2 are designed as follows.

and

with (•)^T denoting the transpose operator. The received signal matrices at receiver 1 and 2 are given in (1), where X₁ and X₂ are given in (2) with H, G, A, B and V_ij for i,j = 1,2 ∈ C^3×3, whereas Y₁ and Y₂ ∈ C^12×3. Due to system symmetry, we focus in the sequel on the decoding at receiver 1. Let y_i, whose j-th element denoted by y_i,j, be the i-th column of Y₁ with conjugate operator applied to rows 9 to 12, then

where H_i and G_i have the same structure. Due to space limit, we give only H_i as follows:

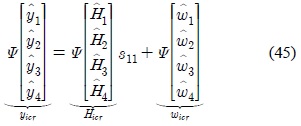
The aligned interference coefficient matrices are given by:

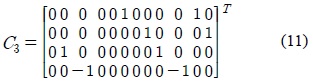
where , for i = 1,⋯,4.

The aligned interference can be simply removed by constructing the set of vectors.

where the system becomes interference-free and is represented by the following equation.

with the 8×4 matrices being derived from H_i and G_i by removing their zero rows.

For the case of n_T = 4, the matrices S_i1 and S_i2 for i = 1,2 are designed as follows.

and

The 12×4 received matrices Y₁ and Y₂ are given as in (1). Rows 9 to 12 are then conjugated and received matrices are remodeled as in (7) as follows.

where H_i and G_i have the same structure. H_i is given by:

In (16), C₁ to C₃ are given in (9) to (10), respectively, while C₄ is given by

Now, let the vectors , for i = 1,⋯,4, be constructed as in (12), then the interference-free system is given by

with the 8×4 matrices being derived from H_i and G_i by removing their zero rows.

In the following, we introduce two decoupling algorithms; the first is an interference cancellation receiver (ICR) based on the work given in [10] and [11], whereas the second algorithm is the linear zero-forcing (ZF), where we shed light on the simplicity of the channel inversion due to the structure of the resulting interference-free system.

3.3.1. Interference cancellation receiver

Let the interference-free system be represented by the following two equations.

where in the case of n_T = 3.

In the case of n_T = 4, the following holds.

To decouple the vector s₁₁, s₁₂ is decoupled similarly, we construct the following two equations.

where ║G║_F is the Frobenius norm of G. Since the matrices in (20) are orthogonal, then subtracting (24) from (23) results in

Let

then

Due the operation completeness of the matrices in 20, is also orthogonal. Then, the estimate of s₁₁ is given by

where Q(•) denoting the vector demodulation operator.

3.3.2. Linear receiver

Let the system in (20) be reformulated as following.

The estimate of the symbols from the transmitters are then obtained using the linear ZF detector as follows.

with the estimate of si1 is given by . Due to the structure of the matrices , for i = 1,⋯,n_R, the following holds.

where the matrices C, D and E are real-valued with C and D being diagonal with diagonal elements equal to , respectively.

Based on the block matrix inverse lemma,

Note that the matrix (C - ED^-1E^H) is a scaled identity matrix, and hence calculating its inverse requires a single real division operation. The same holds for the inversion of the matrices C and D. As such, the complexity of the ZF detection reduces to simple real operations rather than fully computing the inverse of an 8×8 complex-valued matrix.

To achieve higher diversity gains employing a single receive antenna, the conventional Alamouti code [7] with two transmit antennas is extended to the 2^m transmit antennas case with m ≥ 2 [13-15]. In the following, we introduce alignment design and receiver structures for the case of the extended Alamouti with n_T = n_R = 4 built on the system depicted in Figure 1.

In the current design, (2) and (3) still hold with the difference that the matrices V_ij for i = 1,2, A, B, G, and H are of size 4×4, and S_i1 and S_i2, for i = 1,2, are respectively designed as

Based on (1), the 6×4 received signal matrices at receiver 1 and 2 are respectively written as

where , for i = 1,⋯,4. Without loss of generality, we will focus on the decoding at receiver 1, where receiver 2 has the same decoding and performance due to system symmetry. The system in (33) is converted to the equivalent 24×1 vector , where the elements of are filled in row-wise. That is, the first 6 elements of are the first row of Y1, elements 7 to 12 are the second row of Y1. The conjugate operator is applied to rows 3 and 4 before being inserted in .

The aligned interference at receiver 1, i.e., I_i terms, is removed by performing simple addition and subtraction operations on the elements of . To this end, let us define the following 4×1 vectors

where the vectors for i = 1,⋯,4 are derived similarly from Then, with

Note that , for i = 1,⋯,4, have the same structure of the extended Alamouti matrices, which implies that they have the same properties. After aligned interference cancellation, the system can be rewritten as

where the noise is still white with a covariance matrix , where ⊗ denotes the Kronecker product and I₄ is the 4×4 identity matrix.

Before introducing the decoupling schemes, it is worthy to shed some light on the properties of the matrices given in (36), where these properties are essential in the design of the receiver. Let F_i for i = 1,⋯,n have the same structure of the matrices given in (36), then

1) The matrix is real-valued, having the form

where

2) These matrices are complete in terms of matrix addition, matrix subtraction, and matrix multiplication. That is, the Gram matrix of F_iF_j, for j ≠ i, has the same structure explained in Property I. This can be simply proven using the block form of each matrix and perform each of the aforementioned operations.

3) The inverse of given in Property I, has the following form

with

4) The sum of Gramians of the matrices defined in (36) is given by

with

Having that been said about the properties of the matrices given in (36), we introduce the properties of the Gramian matrix which will be used in the decoupling algorithms to be introduced in the sequel. The (8×8) Gramian matrix is given by:

where

Note that the 4×4 matrices C and D have the structure explained in Property 4, while the 4×4 matrix E has the structure given in (36). As such, it comes with no surprise that the inverse of H_f has the same structure given (41), as will be explained later on.

In the literature, several detection techniques have been proposed [10], which can be used to decouple the symbols from different receivers in (37). However, the effective channel matrix, or matrices, in (37) has a special structure that motivates the proposal of modified receivers that take into account the particular structure of these matrices. In the following, we introduce the details of two receiver structures.

4.2.1. Interference cancellation receiver

The idea of the ICR is based on the work introduced in [10] and [11], with the particularity that the system discussed here is not orthogonal. That is, the Gram matrix of in (37) include both diagonal and skew-diagonal elements. As such, to decouple s₁₁ the terms which include s₂₁ should be canceled, where two IC stages are required rather than a single stage as in [10].

A) Cancellation of the diagonal elements: Starting with (38), we construct the following four vectors.

Where based on property 1

where diag() is a skew-diagonal matrix. Subtracting the second equation, i.e., i = 2 in (42), from the first one, and the fourth equation from the third one, cancels the diagonal elements of the channel matrix associated with s₂₁, resulting in the following equations

where

B) Cancellation of the off-diagonal elements: Let (43) and (44) be divided by θ₁ and θ₂, respectively, then subtract the second equation from the first one, results in

where . It is worth mentioning that based on Property II, the structure of is defined by Property I.

Finally, the ZF decoder can be used to recover the transmitted vector s₁₁ as following

where the estimate . Note that can be computed using Property III to reduce the computational complexity.

4.2.2 Linear zero-forcing receiver

The system modeled in (37) is first filtered using resulting in

where , and the subscript f refers to filtered. As such, C and D have the structure given in Property 1, as well as satisfying Property 4, while E satisfies Property II. The transmitted vectors are recovered as follows

To avoid the inversion of the 8×8 matrix H_f, we introduce a cost-effective method to compute the inverse without explicitly inverting H_f. Based on the block matrix inverse lemma, we make the following remarks:

1) C, D, (C - ED^-1E^H), and (D - E^HC^-1E) are real-valued and have the structure given in Property I, which implies that their inverses are simply computed using Property III. The inverse of each of these matrices requires only three operations - two real multiplication and one division operations.

2) E^HC^-1E = C^-1E^HE, where E^HE has the structure given in Property I. The same applies for ED^-1E^H. Using Property II, E^HE can be obtained where 9 multiplication and 6 addition operations are required. Multiplying the result by C^-1 requires 4 multiplication and 2 addition operations.

3) H_f is a Hermitian matrix, which implies that only the elements of an upper triangular matrix are computed.

Based on these remarks, it stems out that the computational complexity of the linear ZF detector is low due to the special structure of the effective channel matrices.

In this section, we consider that each transmitter has full knowledge of only the channels coupling his transmit antennas with those of the two receivers. The elements in the channel matrices are independent and follow the circular-symmetric complex Gaussian distribution with mean and variance of zero and unity, respectively.

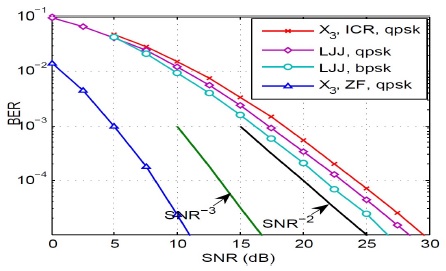
Figure 2 depicts the performance of OSTBC with code rate of 1/2 and n_T, referred to as X₃, built on the system depicted in Figure1.

To hold a fair comparison between the proposed scheme and the LJJ scheme, we fix the spectral efficiency to 8/3 bits/s/Hz, implying that the modulation schemes used for and LJJ schemes are QPSK and BPSK, respectively. Starting with the ICR, due the increased dimensionality of the interference, this receiver fails to achieve the full diversity gain of n_R = n_T = 3. Due to the special structure of the effective channel matrix, as explained in Section III, the simple linear ZF receiver achieves the full diversity order of n_T = n_R = 3 while attaining high gain in the bit error rate. At a target BER of 10^-4, the proposed X₃ outperforms the conventional LJJ schemes by 14dB.

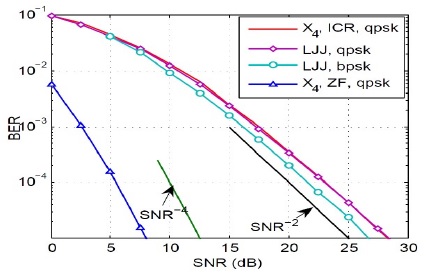
Figure 3 depicts the performance of OSTBC with code rate of 1/2 and n_T = 4, referred to as X₄, built on the system depicted in Fig. 1. Again, for the same spectral efficiency of 8/3 bits/s/Hz, we employ QPSK and BPSK bit-to-symbol mapping for the proposed X₄ scheme and the conventional LJJ scheme, respectively. The ICR shows similar performance as in the case of the X₃ scheme. The simple linear ZF receiver achieves the full diversity order of n_T = n_R = 4 with a gain of about 16.5dB at a target BER of 10^-4.

Finally, Figure 4 depicts the performance of the quasi-OSTBC with n_T = 4, referred to as T₄, built on the system depicted in Figure 1. Since the ICR employed a two-stage SIC scheme to cancel the diagonal and skew-diagonal interference, the performance is therefore even worsen as compared to that in the cases of the X₃ and X₄. Despite the quasi-orthogonality of the effective channel matrices, the linear ZF receiver for the proposed X₄ scheme achieves a superior performance of about 10dB at a target BER of 10^-4 as compared to the LJJ algorithm both employing QPSK modulation, resulting in an equal spectral efficiency of 8/3 bits/s/Hz. Our proposed scheme performs close to the optimum diversity order of n_T = n_R = 4. The small degradation in the diversity order is due to the quasi-orthogonality of the effective channel matrices. A further research will be conducted to optimize the code matrices so as to achieve the full diversity order, or at least to reduce the degradation.

In this paper, we introduced three schemes that achieve superior performances as compared to the conventional LJJ scheme in terms of BER and diversity order all at the same spectral efficiency. The first two proposed schemes, namely X₃ and X₄, employ orthogonal STBCs to generate the code matrices, resulting in orthogonal effective matrices, hence achieving the optimum diversity order of 3 and 4, respectively. The third proposed scheme, referred to as T₄, is superior to the conventional LJJ algorithm in terms of BER and diversity order, however, due to the quasi-orthogonality of the effective channel matrices, the diversity order of this scheme slightly lacks the optimum one.

As a future work, we plan to investigate the implementation of several quasi-OSTBCs with n_T > 4 built on the described system in this paper. Besides, a careful analysis of the diversity gain will be carried out and methods to achieve the optimum diversity order will be introduced.