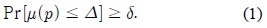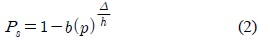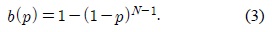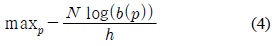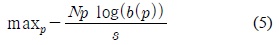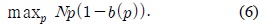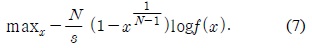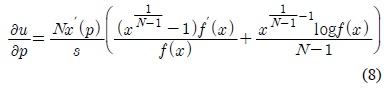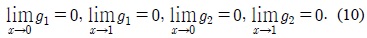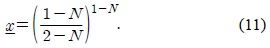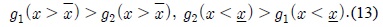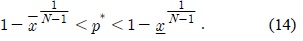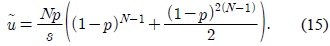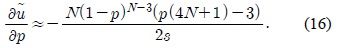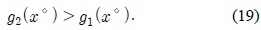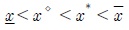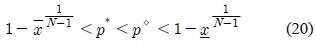네트워크 제어 시스템을 위한 최적화된 매체 접근 확률

doi:10.6109/jkiice.2015.19.10.2457

OA학술지
Journal of the Korea Institute of Information and Communication Engineering

네트워크 제어 시스템을 위한 최적화된 매체 접근 확률 Optimized Medium Access Probability for Networked Control Systems

DOI : 10.6109/jkiice.2015.19.10.2457
Publish: Journal of the Korea Institute of Information and Communication Engineering Volume 19, Issue10, p2457~2464, 31 Oct 2015

ABSTRACT

무선 네트워크를 통한 네트워크 제어 시스템 (NCS: Networked Control Systems)은 다양한 제어 시스템의 효율성을 극대화 할 수 있는 잠재력을 가지고 있다. 본 연구에서는 네트워크 제어 시스템으로부터 이끌어낸 상태갱신주기(SUI: State Update Interval)라는 성능 메트릭을 정의한다. 제시된 상태갱신주기는 제어와 통신 시스템 계층 사이의 핵심적인 상호작용을 포함하고 있다. 제시된 성능 메트릭은 NCS를 위한 최적화 문제를 도출하는데 사용이 되었으며, 이러한 최적화 문제의 목적 함수는 상태갱신주기의 제한 요소를 만족하는 확률이며 변수는 매체접근 확률로 표현되었다. 본 연구에서는 제시된 최적화 문제의 최적 매체접근 확률이 유일한 해를 가진다는 것을 증명하였다. 또한 NCS를 위한 최적의 매체접근 확률은 전송률을 극대화하는 기존의 매체접근 확률보다 낮다는 결론을 도출하였다. 성능 분석 결과를 통하여 시스템의 안정도가 상태갱신주기를 고려한 최적의 매체접근 확률을 사용하였을 때가 전송률을 최대화하는 매체접근 확률을 사용 했을 때 보다 높다는 점을 보였다.

Distributed Networked Control Systems (NCSs) through wireless networks have a tremendous potential to improve the efficiency of various control systems. In this paper, we define the State Update Interval (SUI) as the elapsed time between successful state vector reports derived from the NCSs. A simple expression of the SUI is derived to characterize the key interactions between the control and communication layers. This performance measure is used to formulate a novel optimization problem where the objective function is the probability to meet the SUI constraint and the decision parameter is the channel access probability. We prove the existence and uniqueness of the optimal channel access probability of the optimization problem. Furthermore, the optimal channel access probability for NCSs is lower than the channel access probability to maximize the throughput. Numerical results indicate that the improvement of the success probability to meet the SUI constraint using the optimal channel access probability increases as the number of nodes increases with respect to that using the channel access probability to maximize the throughput.

KEYWORD

무선통신 , 매체접근제어 , 네트워크 제어 시스템 , 상태갱신주기

본문

Collapse all

Ⅰ. 서 론

무선 센서 및 액추에이터 네트워크를 통한 네트워크 제어 시스템 (NCS: Networked Control Systems)은 산업 자동화 시스템, 차량 네트워크 시스템, 항공 교통 시스템과 같은 다양한 스케일의 분산 제어 시스템의 효율성을 극대화 할 수 있는 잠재력을 가지고 있다[1-3]. NCS는 센서, 액추에이터, 제어기가 공간적으로 분산화 되어있으며, 이들이 기존의 point-to-point 연결에서 벗어나 무선 네트워크를 통하여 연결된 시스템을 말한다. 제어 응용 시스템에서 무선 네트워크를 통하여 센서 측정 데이터 및 제어 신호를 전송하게 되면 케이블 설치비용 등을 포함한 시스템 구축 비용을 획기적으로 절약 할 수 있다. 그러나 현재의 무선 네트워크 프로토콜은 이러한 NCS의 안정성을 보장하지 못하는 치명적인 결함을 갖고 있다[1].

네트워크는 제어 시스템의 안정성을 보장하기 위하여 어떠한 불완전한 트래픽 상황, 예측 가능하지 못한 혼잡 및 부분적인 장애에도 항상 적시에 적절한 정보를 전달할 수 있어야 한다. 그러나 제어와 통신 시스템 사이의 복잡한 상호작용을 효율적으로 모델링 할 수 없기 때문에, NCS를 위한 무선 네트워크 프로토콜의 설계는 아직까지 미진한 연구 결과를 보이고 있다. 이러한 문제의 가장 핵심적인 이유는 현재까지 제어와 통신 계층사이의 연구가 상호 유기적으로 진행되지 못한데서 기인한다.

기존 대부분의 연구는 중앙 집중적인 시분할다중접속 (TDMA: Time Division Multiple Access) 기반의 매체접근방식에서 주어진 트래픽 또는 지연 요구 조건에 따른 스케줄링 기법 [4,5]과 제어 시스템의 성능 요구조건을 만족하도록 트래픽 및 지연과 같은 파라미터를 최적화하는 방식에 [6,7] 적용되었다. 따라서 기존에는 제어와 통신 계층이 분리된 형태로 많은 연구가 진행되었다.

본 연구에서는 기존의 연구와 다르게 NCS를 위한 무선 네트워크 프로토콜 설계 방향의 새로운 측면을 고려하고자 한다.

특히, NCS를 위한 경쟁기반 매체접근제어(MAC: Medium Access Control)의 채널 접근 확률에 관한 최적화문제를 다루고자 한다.

본 연구는 주요 4가지 핵심 내용을 포함하고 있다.

Ⅱ. 시스템 모델

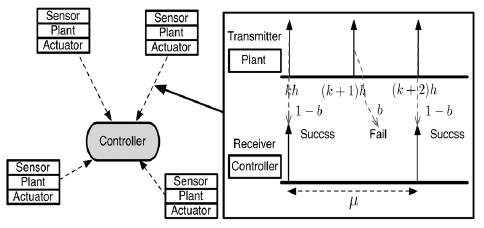
그림 1은 다수의 물리적 시스템들이 무선 네트워크를 통하여 제어가 이루어지는 네트워크 제어 시스템의 구조를 표현하고 있다[8].

[그림 1.] 네트워크 제어 시스템 구조도

기본적으로 각 센서는 물리적 시스템에 부착되어 상태 정보를 읽어 들이고, 이러한 정보를 제어기에 전달하며 계산된 제어 신호는 다시 액추에이터에 전송된다. 따라서 NCS를 위한 무선 네트워크는 센서에서 제어기로 전달되는 상향 링크와 제어기에서 각 액추에이터로 연결되는 하향 링크로 구성된다. 이러한 시스템에서 무선 네트워크는 정보 전송 시에 지연이나 패킷 손실을 가져올 수 있다. 따라서 무선 네트워크의 성능은 NCS의 안정성에 직접적인 영향을 줄 수 있으며, 극심한 네트워크 성능 저하 시 전체 시스템의 안정성에 치명적인 영향을 줄 수 있다[1].

물리적 시스템의 상태 정보는 갱기주기 h에 따라 센서에 의해 샘플링되고 이때 패킷의 전송 손실 확률은 b로 가정한다. 이러한 시스템의 무선 네트워크 부분은 N개의 플랜트 정보가 제어기로 전달되는 Uplink로 생각할 수 있으며, 따라서 N개의 제어 시스템이 공동의 무선 자원을 사용하여 제어 시스템에 정보를 전달하는 하나의 셀 네트워크로 가정할 수 있다. 모든 네트워크의 노드는 시간 동기화가 되어있으며, 패킷의 전송은 슬롯시간의 범위에서만 발생한다고 가정한다. 또한 각 패킷의 전송 시간은 하나의 슬롯 시간과 길이와 같다고 가정한다. 무선 채널은 완벽하다고 가정하여, NCS에 관한 순수한 매체접근방식의 영향을 분석한다.

각 노드는 [1,h/s] 사이의 슬롯 시간을 랜덤하게 선택하여 패킷을 전송하며 이때 s는 슬롯 길이를 의미하고 h/s는 정수값으로 가정한다. 채널 접근 확률은 p = s/h으로 표현하며 0 < p < 1을 가정한다. 따라서 채널 접근 확률은 샘플링 주기에 반비례하는 관계를 가지고 있음을 알 수 있다. 예를 들어 동종의 제어 시스템을 가정하면, 네트워크 노드의 자원 할당 측면에서의 공평성을 고려하여, 모든 노드는 같은 채널 접근 확률 p를 갖게 된다. 각 노드가 패킷을 전송하고자 하면, 샘플링을 통하여 물리적 시스템의 상태 정보를 전송한다. 따라서 성공적으로 전송된 패킷의 총 지연 시간은 패킷 의 전송 시간과 전파 지연 시간의 합으로 표현 된다. 대부분의 제어 응용에서 전송 지연은 샘플링 주기보다 매우 짧다고 할 수 있으며, 따라서 이러한 짧은 지연 시간동안의 물리적 시스템의 변화는 상태갱신주기보다 매우 작다고 가정할 수 있다[1].

패킷 손실은 기본적인 Bernoulli 랜덤 프로세스에 따라 모델이 되었으며, 패킷손실률은 물리적 시스템과 제어기 사이의 확률 b로 가정한다. 같은 슬롯 시간에 두개 이상의 패킷이 전송이 되면 관련된 모든 패킷은 충돌로 인하서 손실된다고 가정한다. 각 노드는 버퍼를 가지고 있지 않다고 가정하여 노드는 절대로 두 개 이상의 패킷을 동시에 가지고 있을 수 없다. 따라서 제어기에 도착하는 패킷은 일정한 시간적 순서를 갖는다. 참고로 일반적인 제어 시스템의 경우 전송에 실패한 패킷을 연속적으로 재전송하는 것은 시스템의 안정화에 크게 도움이 되지 않는다[1].

   2.1. 상태 갱신 주기

기존의 제어 시스템은 주로 연속적인 샘플링에 패킷이 무손실과 무지연의 이상적인 네트워크를 통하여 전송 되는 것을 가정하였다. 그러나 어떠한 무선 네트워크 프로토콜을 사용하더라도 이러한 이상적인 네트워크 성능을 만족 시킬 수는 없다. 특히, 이러한 성능 요구 조건은 경쟁기반 랜덤 매체접근방식의 무선 네트워크에서는 만족시키기 어려운 기술적 한계를 갖고 있다. 경쟁기반 랜덤 접근 프로토콜 미래의 항공 및 교통 관제 시스템과 같은 제어 시스템에서 사용이 되고 있다[2,3].

본 연구에서는 상태갱신주기를 성공적인 상태 정보 업데이트 사이의 경과 시간으로 정의하고 이를 최적화 문제에 사용한다. 즉, 그림 1에서 보는 것과 같이 센서와 제어기 사이의 상향 링크 통신에서 샘플링 된 센싱값이 성공적으로 제어기에 수신된 패킷 사이의 경과 시간을 의미한다. 최근 많은 제어 시스템 연구들은 이러한 NCS의 안정성과 직결되는 최대 허용 가능한 상태갱신주기에 관한 내용을 포함하고 있다[1,9]. 관련 논문에서는 손실 및 지연이 없는 이상적인 네트워크 시스템을 가정하여, 제어 시스템의 안정성을 보장 할 수 있는 최대 허용 가능한 상태갱신주기의 길이를 이끌어 내고 있다. 각 노드는 최대 허용 가능한 상태갱신주기 동안에 적어도 한 개 이상의 패킷을 성공적으로 전송해야만 제어 시스템의 안정성을 보장 할 수 있다. 따라서 최대 허용 가능한 상태갱신주기와 관련한 제약 조건은 다음과 같이 패킷의 신뢰도 요구 조건으로 표현 된다.

여기에서 μ는 상태갱신주기, p는 채널접근확률, Δ는 최대 허용 가능한 상태갱신주기, δ는 이러한 최대 허용 가능한 상태갱신주기 조건을 만족해야 하는 최소 확률 조건이다. 예를 들어, 항공 관제 시스템의 경우 Δ = 4.8s, δ = 0.95와 같은 요구 조건을 정의한다 [10]. 협력 기반 자율주행 차량의 경우는 이보다 더 엄격한 요구조건인 Δ = 4.8ms, δ = 0.95을 갖는다[3].

Δ ≫ h를 가정하면, 시간 Δ동안에 총 전송 기회는 로 근사화 할 수 있다. 따라서 Δ시간 동안에 적어도 하나 이상의 성공적인 전송이 일어날 수 있는 확률은 다음과 같다.

이 제한 조건은 Δ시간 동안에 모든 주기에서 성공적으로 패킷이 전송되어 상태 업데이트가 이루어지는 것을 의미한다. 제어 알고리즘 설계자는 물리적 시스템의 특성에 따라 Δ와 δ를 조절 할 수 있으며, 이러한 제한 조건이 제어와 통신 시스템 사이의 중요한 상호작용을 포함하게 된다.

성공적인 패킷 전송은 하나의 슬롯 시간에 적확히 하나의 노드만 패킷을 전송 할 때 이루어지므로, 네트워크의 패킷 손실률은 다음과 같다.

따라서 b(p)는 N-1개의 다른 노드 중에 적어도 하나의 노드가 같은 슬롯 시간에 전송을 하는 확률을 의미한다.

Ⅲ. 최적화 문제

제어 시스템 설계자에 의하여 Δ와 δ 값이 정해지면, 각 노드는 최적화 문제의 목적 함수인 식(2)의 P_s 확률을 최대화하고자 한다. 따라서 NCS를 위한 최적화 문제는 다음과 같이 표현된다.

여기에서 N은 전체 노드의 수를 의미한다. 이 최적화 문제는 동종의 제어 시스템을 가정하였기 때문에 제어 변수에 독립적인 형태를 갖는다. 채널 접근 확률 p = s/h을 고려한 최적화 문제는 다음과 같이 다시 표현 될 수 있다.

기존의 매체접근제어 관련 연구는 네트워크의 전송량을 최대화하는데 집중되어 있다. 따라서 제안된 NCS를 위한 최적화 문제는 전송량 최대화 문제와 비교 될 수 있다. h ≫ s로 가정하면, 전송량 최대화 문제는 다음과 같이 표현 될 수 있다.

NCS를 위한 최적화 문제의 목적 함수인 식(5)는 전송량 최대화 문제의 목적 함수인 식(6)번과 다른 것을 확인 할 수 있다. 제시된 NCS를 위한 최적화 문제는 전송량 최대화 문제보다는 엔트로피의 최적화 문제와 흡사함을 알 수 있다.

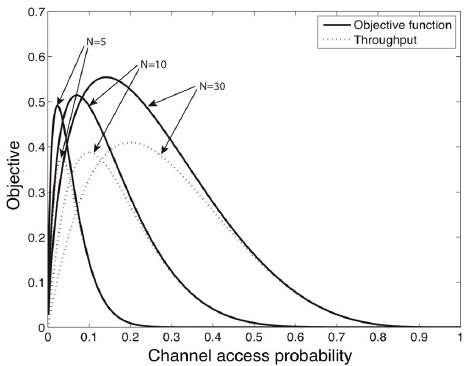
그림 2는 다양한 노드 수와 채널 접근 확률에 따른 NCS 최적화 문제의 목적 함수인 식(5)와 전송량인 식 (6)를 비교하고 있다. 채널 접근 확률이 높을 수 록 트래픽의 양이 늘어나기 때문에 시스템의 상태갱신주기는 최대 허용 가능한 상태갱신주기에 근접함을 확인할 수 있다.

[그림 2.] 다양한 채널 접근 확률과 노드 수에 따른 목적함수 식 (5)과 전송률 식(6)

Ⅳ. 최적 채널 접근 확률

   4.1. 최적화 문제해의 존재성과 유일성

본 절에서는 제시된 최적화 문제의 목적 함수를 최대화 할 수 있는 최적 채널 접근 확률값의 존재성과 유일성을 증명한다.

정리 1: N > 2 일 때, 최적화 문제인 식(5)는 유일한 최적 채널 접근 확률값 p^*를 갖는다.

증명: 먼저 최적화 문제인 식(5)를 재정립하면

여기에서 f(x) = 1 - x 이며 x = (1 - p)^N-1. 최적 해답 조건의 필요조건은 목적 함수 u의 일차 미분이 ∂u/∂p = 0을 만족해야 한다. 목적 함수 u를 p에 대하여 편미분을 하면

여기에서 f′(x) = ∂f(x)/∂X 이며 0 < x 1. 식 (8)에서 0 < p < 1이기 때문에, N > 2 일 때 x′ > 0이다. 가능한 채널 접근 확률의 범주를 고려하여 수식을 재정립하면, 변수 x는 다음 등식을 만족 해야 한다.

여기에서 이며 g₂ = (1-x)log(1-x). 먼저 변수 x에 대하여 함수 g₁과 g₂가 컨벡스 함수임을 증명하고자 한다. 함수 g₁의 이차 미분이 양수이므로 , g₁은 컨벡스 함수이다.

또한, N > 2일때 이므로, 함수 g₂는 컨벡스 함수이다. 변수 x에 대한 함수 g₁과 g₂의 극한은 다음과 같다.

두 함수 g₁과 g₂는 변곡점 에서 부등식의 관계를 가지며, 관련 함수 g₁과 g₂의 변곡점을 다음과 같이 계산할 수 있다. 변수 x에 대한 함수 g₁의 편미분 값은

따라서 함수 g₁의 변곡점은 다음과 같다.

비슷한 방식으로 함수 g₂의 일차 미분값 을 이용하면, g₂의 변곡점은

여기에서 N > 2 일 때 이다. 따라서 켄벡스 함수인 g₁과 g₂의 부등 관계는

유일한 해답 x^*는 구간 에서 존재하며, 여기에서 x^*는 식(9)으로부터 수치법을 통하여 계산할 수 있다.

x^*가 목적 함수의 유일한 최대값이며 p와 x사이에 일대일 매칭의 관계가 성립하기 때문에, 목적 함수를 최대화하는 최적의 채널 접근 확률 p^* 또한 유일한 값이 된다. 따라서 x^*에 상응하는 최적 채널 접근 확률값 p^*는 다음과 같다.

이것으로 정리에 대한 증명을 마무리한다.

   4.2. 대체 방안

정리 1의 증명에서 확인 했듯이 최적의 채널 접근 확률 p^*는 비선형 방정식을 풀어서 얻어 낼 수 있다. 이러한 해결책의 문제점은 p^*의 값을 복잡한 수치 해석법을 사용해야만 얻을 수 있다는 것이다. 그러나 이러한 방식을 임베디드 디바이스에 적용하기에는 그 계산 복잡도가 매우 높아 구현하기에 적당하지 않다. 따라서 식 (5)의 로그 함수에 테일러 급수를 적용하여 관련 식을 간소한 후, 대체 가능한 최적 채널 접근 확률값을 계산하고자 한다. log b(p) 는 식(5)의 비선형 관계의 주요원인이 되는 부분이며, 테일러 급수에서 처음 2개의 시리즈 만을 고려하여 목적 함수를 간소화하면

N > 2 인 노드의 수를 고려하면, (1-p)^N-1 ≈ 1와 p² ≈ 0 같은 간소화가 가능하다. p에 대한 ũ 함수의 편미분을 간소화하면

N > 2 에서 가능한 영역인 0 < p < 1를 고려하면 대체 가능한 채널 접근 확률은 다음과 같다.

   4.3. 비교

본 절에서는 NCS를 위한 최적화 문제의 최적 채널 접근 확률 p^*과 전송률을 최대화 할 수 있는 채널 접근확률 p^⋄을 비교하고자 한다. 일차 미분의 최적화 필요조건을 고려하여 전송률을 최대화 할 수 있는 채널 접근 확률은 다음과 같다.

정리 1의 증명에서 컨벡스 함수 g₁과 g₂는 x^⋄ = (1-p^⋄)^N-1에서 다음과 같은 부등의 관계를 갖는다.

따라서 NCS의 안정성을 위한 최적의 채널 접근 확률은 전송률을 최대화하는 채널 접근 확률보다 낮다는 것을 알 수 있다.

Ⅴ. 성능 분석

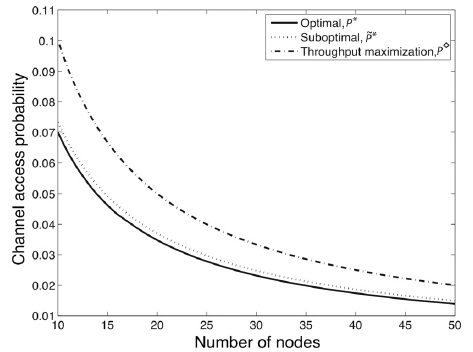
본 절에서는 NCS를 위하여 제안된 최적 채널 접근 확률과 기존의 네트워크 전송량 최대화를 위한 채널 접근 확률의 성능을 비교 분석한다. 그림 3은 식(9)의 최적 채널 접근 확률 p^*, 식(17)의 대체 가능한 채널 접근확률 , 식(18)의 전송률을 최대화하는 채널 접근 확률 p^⋄을 다양한 노드의 수에 따라 비교하고 있다. 최적 채널 접근 확률 p^*는 노드의 수가 늘어남에 따라 감소하는 것을 확인 할 수 있으며, 최적 채널 접근 확률 p^*는 p^⋄ 보다 낮은 것을 확인 할 수 있다. 또한, 대체 가능한 채널 접근 확률 는 최적 채널 접근 확률과 거의 비슷하다는 것을 확인 할 수 있다.

[그림 3.] 채널 접근 확률

제어 시스템의 특성을 정량적으로 정규화하기 위하여, 시스템 지표 β를 최대 허용 가능한 상태갱신주기 Δ와 슬롯 시간의 크기 s의 비로 정의하였다. 성능 지표 β가 0에 가까울수록, 제어 시스템은 빠른 샘플링울 필요로 하는 제어 시스템임을 의미한다.

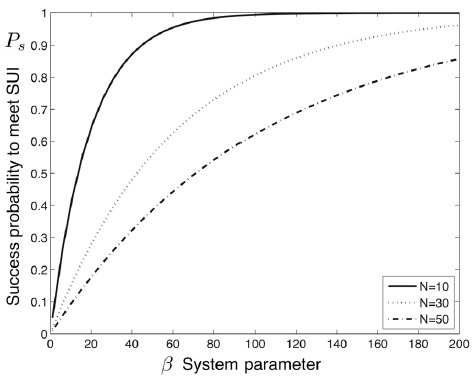
그림 4는 Monte-Carlo 시뮬레이션을 통한 최대 허용 가능한 상태갱신주기 요구 조건을 만족하는 확률을 다양한 노드 수와 β 값에 따라 표현하고 있다.

[그림 4.] 최대 허용 가능한 상태갱신주기의 요구 조건을 만족하는 확률

NCS의 요구 조건을 만족하는 확률은 높은 β 일수록 증가함을 확인할 수 있다. N = 30 과 같이 많은 노드 수의 노드로 이루어진 네트워크의 경우 높은 간섭으로 인하여, 요구 조건 만족 확률이 0.9 보다 낮음을 확인할 수 있다. 높은 β > 120 와 적은 노드 수 N = 10 에서는 요구 조건을 만족하는 확률이 거의 1에 접근하는 것을 확인 할 수 있다.

NCS를 위한 최적화 문제의 최적 채널 접근 확률 p^*와 전송률을 최대화하는 채널 접근 확률 p^⋄를 사용하였을 때의 요구 조건 만족 확률의 차이에 기반하여 성능 이득을 정의할 수 있다.

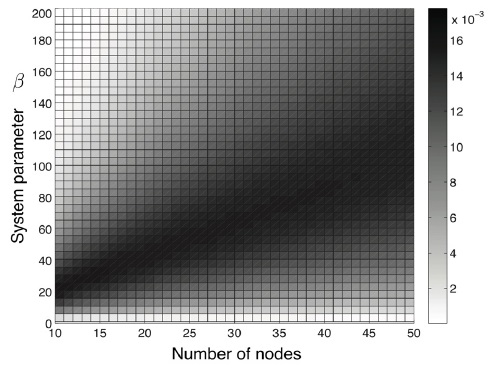
그림 5에서는 다양한 노드 수와 β 값에 따라 이러한 성능 이득을 시뮬레이션을 통하여 표현하고 있다. 비록 성능 이득이 노드 수 및 β 값과 높은 상관관계를 가지고 있으나, 최적 채널 접근 확률 p^*를 사용했을 시 채널 접근 확률 p^⋄를 사용 했을 때보다 높은 성능을 보이고 있는 것을 확인 할 수 있다. 또한 높은 β > 120와 적은 노드 수 N < 20의 경우 요구 조건을 만족 시키는 것이 어렵지 않기 때문에 성능 이득이 그리 높지 않음을 확인 할 수 있다. 최적의 채널 접근 확률은 최대 허용 가능한 상태갱신주기의 요구 조건을 만족하는 확률을 향상 시킬 수 있으나, β ≤ 5와 같이 매우 빠른 제어 시스템의 안정성을 보장하기에는 충분하지 않다. 따라서 제어시스템이 빨라질수록 간단한 경쟁 기반의 매체접근제어 방식의 무선 네트워크 프로토콜로는 NCS의 안정성을 보장 할 수 없는 것을 확인할 수 있다.

[그림 5.] SUI 조건을 만족하는 확률의 성능 이득

Ⅵ. 결 론

본 연구는 네트워크 제어 시스템을 위한 무선 네트워크 프로토콜의 최적화 방안을 제시하고 있다. 특히, 상태정보갱신주기라는 성능 메트릭을 사용하여 제어시스템의 네트워크 요구 사항을 만족시킬 수 있는 효율적인 무선 네트워크의 매체접근방안을 제공하였다. 이러한 방안의 핵심은 최적화 문제에 기반하는데, 문제의 목적 함수는 상태갱신주기의 제한 요소를 만족하는 확률이며 변수는 매체접근 확률로 정의되었다. 제시된 최적화 문제의 최적 채널 접근 확률값은 그해가 유일하다는 것을 수학적으로 증명 하였다. 또한, 네트워크 제어 시스템을 위한 최적 채널 접근 확률이 기존의 전송률을 최대화 하는 채널 접근 확률보다 낮다는 것을 증명하였다.

성능 분석 결과는 시스템의 안정도가 상태갱신주기를 고려한 최적의 매체접근 확률을 사용하였을 때가 전송률을 최대화하는 매체접근 확률을 사용 했을 때 보다 높다는 것을 보이고 있다.

참고문헌

1. Hespanha J. P., Naghshtabrizi P., Xu Y. 2007 “A survey of recent results in networked control systems,” [Proceedings of the IEEE] P.138-162
2. Park P., Khadilkar H., Balakrishnan H., Tomlin C. 2014 High Confidence Networked Control for Next Generation Air Transportation Systems [IEEE Transactions on Automatic Control] Vol.59 P.3357-3372
3. Vinel A. 2012 “3GPP LTE versus IEEE 802.11p/WAVE: Which technology is able to support cooperative vehicular safety applications?” [IEEE Wireless Communications Letters] Vol.1 P.125-128
4. Gupta R. A., Chow M. 2010 "Networked control system: Overview and research trends," [IEEE Transactions on Industrial Electronics] Vol.57 P.2527-2535
5. Pereira N., Andersson B., Tovar E. 2007 "Widom: A dominance protocol for wireless medium access," [IEEE Transactions on Industrial Informatics] Vol.3 P.120-130
6. Liu X., Goldsmith A. 2004 "Wireless network design for distributed control," [in IEEE Conference on Decision and Control] P.2823-2829
7. Wu Y., Buttazzo G., Bini E., Cervin A. 2010 "Parameter selection for real-time controllers in resource-constrained systems," [IEEE Transactions on Industrial Informatics] Vol.6 P.610-620
8. Park P. 2015 "Traffic Generation Rate Control of Wireless Sensor and Actuator Networks," [IEEE Communications Letters] Vol.19 P.827-830
9. Carnevale D., Teel A. R., Nesic D. 2007 “A Lyapunov proof of an improved maximum allowable transfer interval for networked control systems,” [IEEE Transactions on Automatic Control] Vol.52 P.892-897
10. Park P., Tomlin C. 2015 "Performance Evaluation and Optimization of Communication Infrastructure for the Next Generation Air Transportation System," [in IEEE Transactions on Parallel and Distributed Systems] P.1106-1116