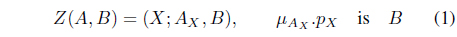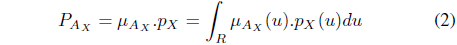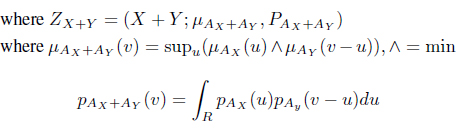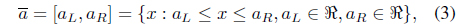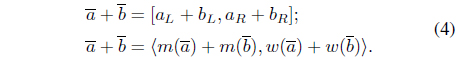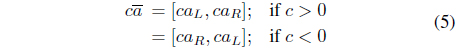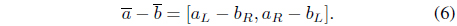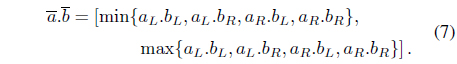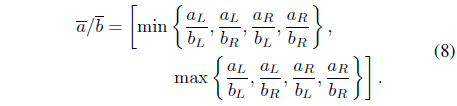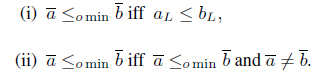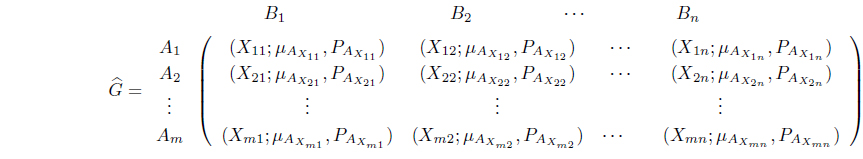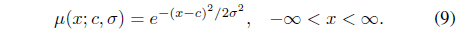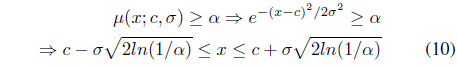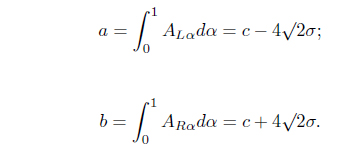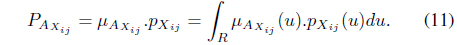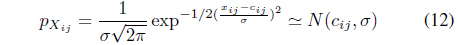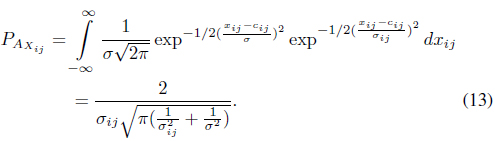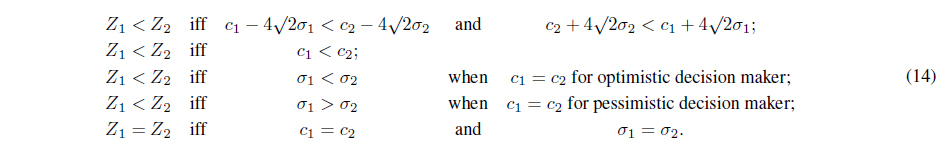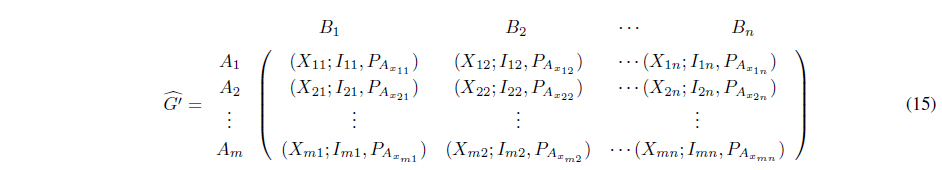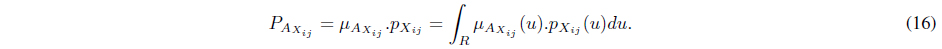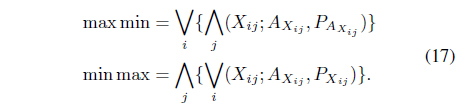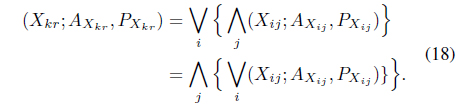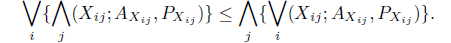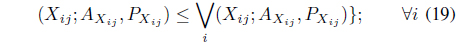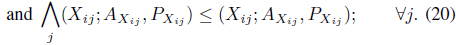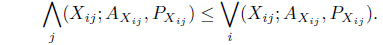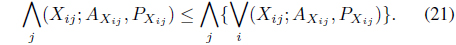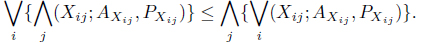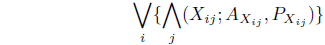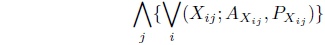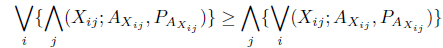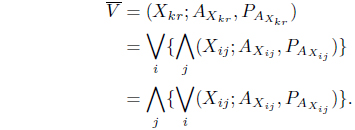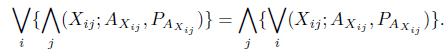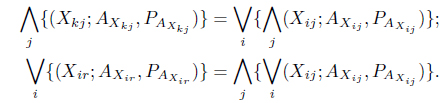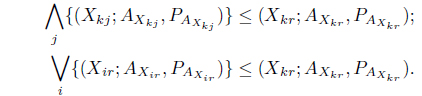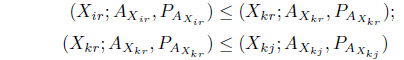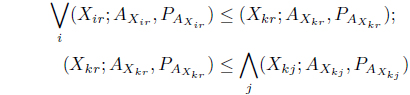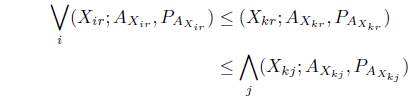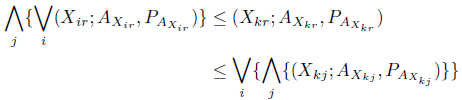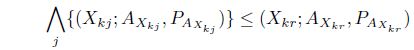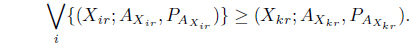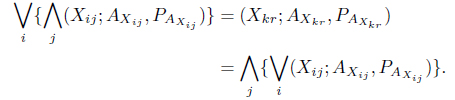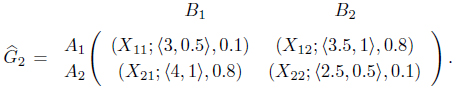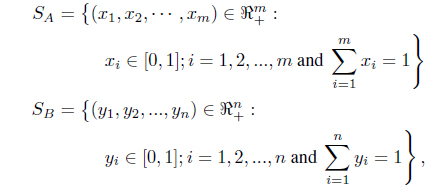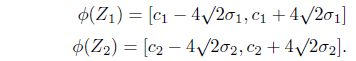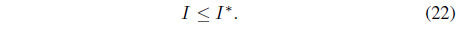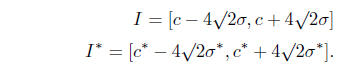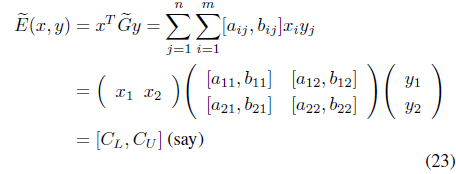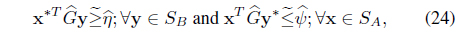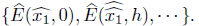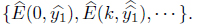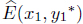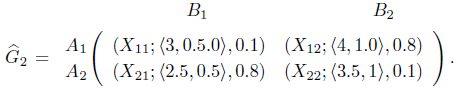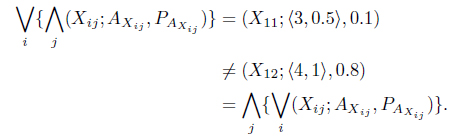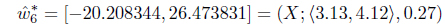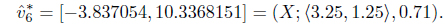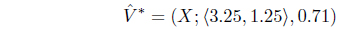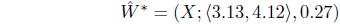In this paper, a matrix game is considered in which the elements are represented as Z-numbers. The objective is to formalize the human capability for solving decision-making problems in uncertain situations. A ranking method of Z-numbers is proposed and used to define pure and mixed strategies. These strategies are then applied to find the optimal solution to the game problem with an induced pay off matrix using a min max, max min algorithm and the multi-section technique. Numerical examples are given in support of the proposed method.
In the modern world, one is faced with innumerable problems arising from existing socioeconomic conditions that involve varying degrees of imprecision and uncertainty. We often need to take decisions in conflicting situations based on uncertain, ambiguous, or incomplete information. Human beings have a tremendous capability to form rational decisions based on such imprecise information. It is hard to formalize these human capabilities. This challenge has motivated us to consider a game theoretic model under conditions of uncertainty.
Game theory problems under uncertainty have been considered by many researchers, e.g., Nayak and Pal [1–3], Narayanan [4], and Nishizaki [5]. Narayanan [4] solved a 2 × 2 interval game using the probability and possibility approach but no certain distribution function has been used. Nayak and Pal [3] established a method of solution of a matrix game using interval numbers. But the solution has been considered under a certain condition which has been obviated by the authors in their work [6]. Biswas and Bose [7] constructed a quadratic programming model under fuzzily described system constraints on the basis of degree of satisfaction. Veeramani and Duraisamy [8] suggested a new approach for solving fuzzy linear programming problem using the concept of nearest symmetric triangular fuzzy number approximations with preserve expected interval. But this approach is not efficient when a primal basic feasible solution is not in hand. Ebrahimnejad and Nasseri [9] overcame this shortcoming using a new algorithm. Iskander [10] proposed a new approach for solving stochastic fuzzy linear programming problem using triangular fuzzy probabilities. Apart from this Kumar and Kar [11], Marbini and Tavana [12], Ebrahemnijad and Nasseri [13] have contributed substantially to the application of fuzzy mathematics in operations research. However, there are many shortcomings in the above-mentioned techniques for solving game problems in uncertain situations. These can be categorized as follows:
We consider the theory of fuzzy sets to address the uncertainty that occurs in industrial problems or machine learning. It is unlikely that we always have complete knowledge about the domain set. For example, when we try to address an object as ‘beautiful,’ we may not have complete knowledge about the parameters by which the beauty of an object can be explained, or the parameters, if assumed, may not match other people’s choices, i.e., they may not be unique. However, the reliability of the information must be taken into consideration, and this aspect is lacking in the fuzzy set description. We use soft set theory or rough set theory to describe uncertain situations. However, we may not know the complete set of parameters E in the case of a soft set, i.e., there is an issue regarding the reliability of the information concerned. In the rough set description, the lower or upper approximation or boundary region may not always be described, because knowledge or information about the equivalence relation R or domain U are only approximations or assumptions, and may not be known in advance. Additionally, it is not guaranteed that the desired optimal solution will be compatible with industrial applications. Different optimization techniques give rise to different optimal results, and we can only compare these results with those obtained by existing techniques. We cannot, however, ensure that a technique gives an actual optimal solution that will be universally accepted. The main reason behind this is that we cannot address the uncertainty properly, and thus use a number of assumptions.
Thus, we need to develop the mathematical structures that provide a generalization of uncertain situations and that consider the reliability of available information. Zadeh [14] has made an attempt towards such a generalization by proposing Z-numbers. A Z-number is an ordered pair (
The remainder of this paper is organized as follows. In Section 2, we discuss the concept of Z-numbers, before presenting some basic definitions, notation, and comparisons related to interval numbers in Section 3. In Section 4, a matrix game with Z-numbers is proposed, and then Section 5 discusses the interval approximation of Z-numbers, and introduces some definitions, explanations, theorems about matrix games with Z-numbers, pure and mixed strategies, and saddle points. In section 6, a computational procedure is proposed along with a min-max algorithm, max-min algorithm, and multi-section technique. Section 7 presents an example in support of the proposed method, along with discussions related to our algorithm and the results of the numerical example. Brief conclusions are given in Section 8.
Let us consider a fuzzy set defined over a universe of discourse
where,
prob(
This situation, inspires us to define a
where,
Here, we recall that
To consider an arithmetic operation, let
Let us consider that ℜ represents the set of all real numbers. We define an interval, Moore [16], as
where
For,
The order relation of interval numbers is discussed in several literature [16, 17]. Recently Chakrabortty et al. [18] proposed a revised definition of order relations between interval costs(or times) for minimization problems and interval profits for maximization problems for optimistic and pessimistic decision making. Let us suppose, the intervals and represent the uncertain interval costs (or times) or profits in center-radius form.
For minimization problems the order relation ‘ ≤
This implies that is superior to and is accepted. This order relation is not symmetric.
In pessimistic decision making, the decision maker expects the minimum cost/time for minimization problems according to the principle ‘Less uncertainty is better than more uncertainty’.
For minimization problems, the order relation ‘ <
(i) iff , for type-I and type-II intervals, (ii) iff and , for type-III intervals.
which is said to be matrix game with Z-numbers.
In this paper, arithmetic operations on interval [
Now, we define an
and let us consider that and . Let [
Therefore, if
Here, we get the probability density function
where . Then, we obtain from Eq. (9) that
Now, let us consider two
Suppose, the pay-off for player
where ,
Theorem 4.1.
In the context of Z-number, a pure strategy may be considered as a decision making rule in which one particular course of action is selected with some degree of reliability or certainty for the pay off considered. Actually, Z-number gives higher level of generality compared to interval numbers where length of the interval actually measures the certainty. For lack of informativeness of Z-number, we develop the concept of pure strategy in the domain of interval numbers with parallel computation. For matrix game with Z-number, we define the min max and max min as
where ‘∨
Definition 4.1. (Saddle Point) The concept of saddle point in classical form was proposed by Von Neumann and Morgenstern [20]. The (
The position (
Theorem 4.2.
From (19) and (20) we have,
Here, we see that is independent of
Again, the right-hand side of (21) is independent of
Hence the theorem.
Theorem 4.3.
Let
As, , we have . Also, using the order relation over Z-numbers in
This is one of the conditions for (
or,
or,
or,
as
and
Using the above Theorem 4.2 we have,
Hence the necessary and sufficient condition for the existence of a saddle point is proved.
Example 4.1. Let us consider the 2 × 2 matrix game with Z-number having the pay-off matrix as in the following:
It can be easily verified that Therefore, the matrix game with Z-number has a saddle point at (1, 1) and the optimal strategies for players
In a situation where the saddle point of a pay off matrix does not exist we allow mixed strategies to get a solution. In mixed strategies, the probability with which a player chooses a particular strategy is considered. In the context of Z-number, we can say that in mixed strategy game we find an expected pay off with some reliability or certainty of the pay off obtained. Suppose and be the
respectively. Vectors x ∈
Theorem 4.4.
Using interval arithmetic, we can easily verify that
Similarly, using interval arithmetic, we can easily verify that for every interval
Now, let us construct
Using equation (4.2) we have either
Since,
Definition 4.2. (Interval expected pay-off ): If the mixed strategies x = (
where,
CL = (a11 + a22 − b12 − b21)x1y1 + (a12 − b22)x1 + (a21 − b22)y1 + a22 CU = (b11 + b22 − a12 − a21)x1y1 + (b12 − a22)x1 + (b21 − a22)y1 + b22
The composition rules on interval numbers [6] are used in this definition (3) of expected pay-offs.
Definition 4.3. Suppose, and be two intervals defined over ℜ. Let us consider that there exist strategies x∗ ∈
then, x ∈
Let
Definition 4.4. Let us consider that there exist two reasonable values and If there do not exist reasonable values and such that they satisfy both and , then is said to be a solution of the interval matrix game ; x∗ is called an optimal (or a maximin) strategy for player
In this section, we discuss the computation procedure to find out the solution to a matrix game with Z-number. We first transform (through approximation) the pay off matrix with Z-numbers to a pay off matrix with corresponding interval-number. We then use multisection technique and min max algorithm [6] to solve the matrix game. The multisection algorithm is formulated according to the approach given in the work of Chakrabortty et al. [18]. The concept of multisection is inspired by the concept of multiple bi-section, where more than one bi-section is made at a single iteration cycle. The basis of this method is the comparison of intervals (as described in Section 3 of this paper) according to the decision makers point of view.
Algorithm for multisection technique
Input:
Output: Probability
Step 1://calculation of step lengths//calculate step length
end for
Step 2://Division of concerned region into equal subregions //
Step 2.1: For
Step 2.2: //Call the function
Section 3,
Calculate
obtained by as in Eq.
(23)
Calculate
obtained by as in Eq.
(23)
Step 2.3: For
Step 2.4: Calculate
obtained by as in Eq.
(23) at
Calculate
obtained by as in Eq.
(23) at
Calculate
obtained by as in Eq.
(23) at
Calculate
obtained by as in Eq.
(23) at
Step 2.5: Applying required order relation (defined in Section 3)
between any two interval numbers [
end
Step 2.6: Choose the subregion
Step 3: //calculation of widths//.
Step 3.1: Calculate widths
Step 3.2: While
break
Step 3.3: Set
Return to step 2.1
end for
endwhile.
end
Output
END MULTISECTION
On the basis of this technique we have developed an algorithm for max min and min max solutions of a single objective interval game.
Algorithm for min max principle
We conduct operations not on the degree of certainty
Step 1: Put
Step 2: For
Find max/optimistic order relation of ,
where 0 ≤
Step 3: Let the solution set for
Using pessimistic order relation find minimum of
Suppose it occurs at
Step 4: Calculate
Step 5: Using pessimistic order relation calculate for 0 ≤
by multisection technique. Suppose, the minimum value is (say).
Then (by Theorem 4.2) and
Therefore (
Algorithm for max min principle 4.2.1
Step 1: Put
Step 2: For
Find min/pessimistic order relation of
where 0 ≤
Step 3: Let the solution set for
Using optimistic order relation find maximum of
Suppose it occurs at
Step 4: Calculate .
Step 5: Using optimistic order relation calculate
by multisection technique. Suppose the maximum value is (say).
Then (by Theorem 4.2) and
Therefore e (
Thus is a reasonable solution of the interval matrix game , is player
Suppose, a company conducts an opinion pole about an election. They place some questions in front of the voters and get answers as ‘We are not very sure that the candidate A’s honesty is high’ or ‘It is very likely that inflation during the period of the present government is high’. In such cases, we can consider the statements as (A’s degree of honesty, high, not sure) or (price hike, high, very likely). These conditions are representation of Z-numbers. When this happens between two candidates in an election, then it forms a matrix game with Z-number. Suppose, the pay-off matrix is given by
What are the optimal strategies and what is the value of game?
This is an example of 2 × 2 matrix game with Z-number which has no saddle point because
Using the definition of interval expected pay off (4.2) When we run min max and max min programmes in TURBOC we get the reasonable solutions as
and
In this example, we obtain a reasonable solution
and
as respectively gain-floor and loss-ceiling of players
(i) Here the pay off actually means some restriction on the measure of possibility that one can gain or loose with some degree of certainty and value of the game actually means measure of possibility of a solution to be an optimum solution. (ii) We have tried to arrive at a reasonable solution with some degree of certainty which is compatible with the real world situation as most of the optimization results obtained with other numbers or intervals lack some compatibility with the real world situation. For example, there are several kinds of imprecisions. What imprecision will then be modelled using a particular approach is a matter of concern as compared to the existing techniques [6]. In our approach, we have tried to consider a typical imprecision by using Z-number. (iii) We have tried to arrive at a higher degree of generality in the decision making process by using Z-number.
In a decision-making process, the information is often found to be imprecise, incomplete, e.g., ‘about 5%’, ‘high price” etc. In such a situation it is unlikely that usual approach would give a desired result. Again, formalization of the imprecision hardly occurs in our optimization models and there is no universal model which can consider all types of imprecisions. We often model certain types of imprecise data with certain type of membership function or interval numbers. It does not, however, ensure the optimization universally, i.e., there may be a chance to arrive at a better optimal solution if we model it otherwise. So, there is a need for formalization of imprecision and for that purpose we have used Z-number as a pay off which actually gives the degree of certainty. On the restriction of the measure of possibility of pay off one would gain or loose. Though we have modelled a Z-number with a particular type of membership and density function there is scope of further generalization. There is also scope for using this procedure to solve multi-objective decision-making problems.