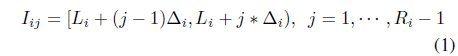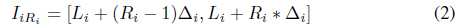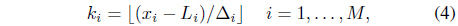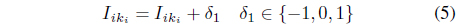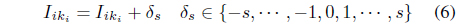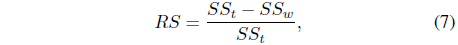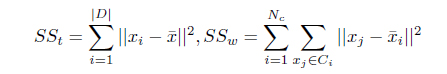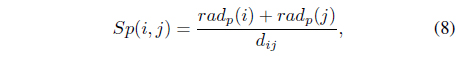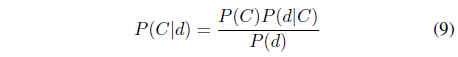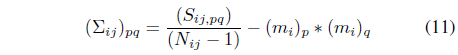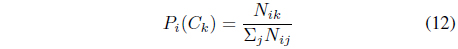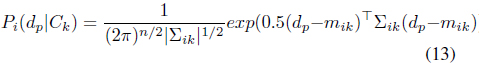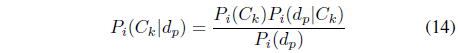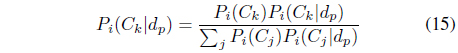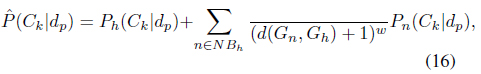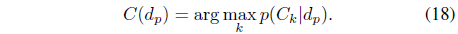The recent technological advances in sensors and storage devices, as well as the advent of various multimedia-based applications, mean that huge volumes of data are accumulated, which need to be processed. Big data present new practical and theoretical challenges in terms of the volume of data, the variety of data types, and the speed of processing. Thus, various platforms and algorithms have been developed and put into practice to address these issues [1, 2, 5, 6].

In the present study, we address the problem of constructing classifiers from a big data training set that comprises continuous attributes. As the volume of data increases, classification techniques that require multiple-pass processing experience severe resource demands. Thus, existing algorithms can be parallelized to handle this problem, or new single-pass algorithms need to be developed. In general, many machine learning algorithms assume that the training dataset is not large and they have been developed for training datasets that are moderate in size. Indeed, some of these techniques are not considered to be applicable to high dimensional data due to the curse of dimensionality. However, big data application domains can be free from the curse of dimensionality because the volume of data is sufficiently large.

The k-nearest neighbor classification methods determine the class of data objects based on the class distribution of proximity-based nearest neighbors [7]. They do not require any preliminary training of a classifier because they determine the classes of data objects based on the class distributions of their neighbors. These methods might not be good choices in the big data application domain because they take a long time to locate the nearest neighbors and to compute the distances between the query data objects and the data objects in the training dataset. Grid-based approaches partition the data space into regularly organized grid cells [8] and they can handle a dataset in cell units instead of individual data objects. In the present study, we propose a classification method that exploits the concepts of k-nearest neighbor classification, grid-based partitioning, and Bayesian inference, which can be applied to big data classification. To handle big data in an efficient manner, some parts of the proposed method are implemented using the MapReduce paradigm [1] in the Hadoop framework [2].

The remainder of this paper is organized as follows. Section 2 provides a brief introduction to the Hadoop framework and the MapReduce programming paradigm, as well as k-nearest neighbor classifiers. Section 3 explains the proposed method for building a classifier from big data with continuous attributes. Section 4 presents some experiment results obtained using the proposed method and Section 5 gives our conclusions.

Considerable amounts of time and space are required to handle large volumes of data. Occasionally, it might not be possible to accommodate a large dataset on a single computer. This is one of the main reasons for using a distributed file system, where a file system can be networked among multiple servers to manage big files. The servers in the distributed file system need to be robust against failure because a failure at any point could cause the entire system to malfunction. Thus, the files are partitioned into blocks and multiple replicas of the blocks are stored in different servers. Hadoop is an Apache project for a distributed computing platform and it provides a distributed file system called the Hadoop Distributed File System [2].

It is not sufficient to process or analyze big data to obtain a distributed file system. Instead, it is necessary to produce a framework for developing distributed parallel processing applications that can handle big data files. A simple approach to performing a task in a distributed, parallel manner is to decompose the task into independent subtasks, where they can be processed without communication between them. The MapReduce model [1] is a programming paradigm that allows a program to be organized with independently executable processing modules called map and reduce. map is an operation that takes an input and produces one or more pairs of (key, value), where key usually acts as the identifier of a pair for which value’s are later collected. reduce is an operation that processes the values with the same key. The map functions cannot share any information, which allows multiple instances to be executed simultaneously for different parts of the input data. To employ the MapReduce paradigm in data processing, we need to devise a method for describing data processing tasks as a sequence of map and reduce operations, which requires a suitable algorithm. The map and reduce operations are paired, but sometimes it is not sufficient to have a pair of map and reduce. In this case, a pair of map and reduce can be chained, where the reduce output from the preceding phase is used as an input for map in the following phase.

To execute MapReduce-based programs, a framework is required to deploy them in a distributed system and to manage resources, such as instantiating multiple map and reduce tasks, delivering data from and to the distributed file system, recovering from failure, and monitoring the status of the working tasks and the networks. Hadoop provides an efficient framework for running MapReduce-based programs [2].

The k-nearest neighbor classifiers comprise nonparametric classification methods for classifying data objects based on the k closest training data objects in the data space. They classify a data object based on a majority vote among its neighbors, i.e., the k nearest neighbors of the data object. These methods do not construct explicit classifier models and they determine the class labels of incoming data by referring to their neighbors on the fly. These approaches are among the simplest machine learning classifiers.

When a query data object arrives, a search is performed to find the k nearest neighbors to the object. The distances between the query object and training data objects in the training set must be evaluated to determine the neighbors. Various distance measures for numeric data have been developed such as the Euclidean distance, Manhattan distance, Mahalanobis distance, and cosine distance [8]. If the data contain categorical attributes, other distance measures are needed such as the Jaccard distance and Tanimoto distance [14].

If the data occupy a high dimensional space and the number of data objects is large, it is not easy to locate the k nearest neighbors. Thus, several data structures have been developed for indexing neighbors, e.g., k-d tree, hierarchical k-means, ball tree, spill tree, and spatial tree [11]. However, the performance of the indexing structure degrades as the volume of data increases. To overcome this difficulty, locality-sensitive hashing techniques [11] have been developed, which use hashing functions to make similar data objects collide in the same or neighboring buckets. These techniques require the maintenance of special hashing structures to record the data objects that belong to each bucket.

In this study, we consider a classification problem for a dataset that comprises numeric data with continuous attributes. Each training data object is labeled with its class. The volume of data can be huge and thus we cannot construct classifiers by scanning the training data multiple times in practical applications. The volume of data can be a bottleneck for conventional k-nearest neighbor classifiers. Thus, we propose a new k-nearest neighbor classification method where we employ grid partitioning of the data space and Bayesian inference to make class decisions. To process big data in an effective manner, the time-consuming tasks in the proposed method are implemented using MapReduce operations.

It is assumed that the dataset D = {d_i|i = 1, . . . , N, d_i = (a_i1, . . . , a_iM; c_i)} comprises a collection of data d_i with M numeric attribute values (a_i1, . . . , a_iM) with class label c_i . Thus, there are M attributes (A₁, . . . , A_M) such that a_ij ∈ Range(A_j) = [L_j,U_j], i = 1, . . . , N, j = 1, . . . , M. Each data object has a class label, s.t., c_i ∈ {K₁, . . . , K_p}.

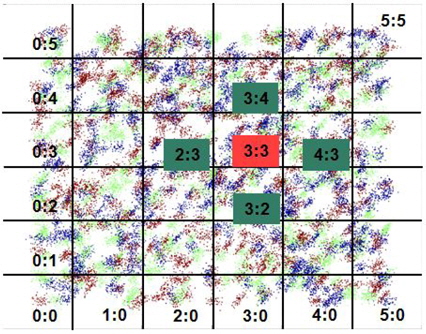
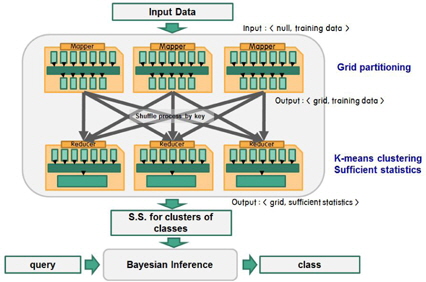
To handle large volumes of data, the proposed method organizes the data space into a grid structure where the dimension of each attribute is partitioned at equidistant intervals. This partitioning process divides the data space into cells, where each cell maintains the class-wise statistical information for the data subset that belongs to the cell. Instead of using individual training data objects, the method models them based on the probability distributions of each class. The classification of query data is performed by Bayesian inference using the prior probabilities and likelihoods of the neighboring cells of the query data.

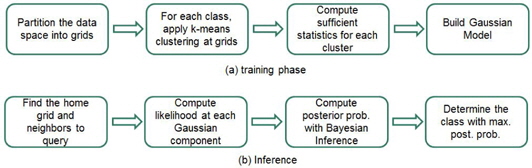
The proposed strategy has two phases: the training phase and inference phase. The inference phase comprises the following steps.

Step 1. Partition the data space into grids. Step 2. Apply the k-means clustering algorithm to class-wise data in the grids with different numbers of clusters. Determine the appropriate number of clusters for each class in the grids. Step 3. Compute the statistics for each cluster. Step 4. Build Gaussian models of the grids.

After constructing Gaussian models for the grids, class inference is performed for a query according to the following sequence.

Step 1. Find the home grid and the neighbors of a query. Step 2. Compute the likelihoods of the query for each Gaussian component. Step 3. Compute the posterior probabilities of the classes by Bayesian inference. Step 4. Determine the class of the query with the highest posterior probability.

The continuous attribute domains are partitioned into several intervals, e.g., equidistant intervals, user-specified intervals, equi-frequency intervals, or data distribution-based partitions. Data processing is straightforward for equidistant interval partitioning and user-specified partitioning, but equi-frequency interval partitioning requires that the attribute values are sorted, which is a computationally intensive task. Distribution-based partitioning requires some baseline information for each attribute, such as the means and standard deviations.

The proposed method partitions each attribute dimension at an equidistant interval. If we suppose that attribute A_i(i = 1, ··· , M) with the range [L_i,U_i ] is partitioned into R_i intervals, then the j-th interval I_ij of A_i is the following interval.

Each attribute may have a different numbers of intervals. A cell in the data space is indexed by (k₁, k₂, ··· , k_M), where the corresponding cell is specified by the intervals (I_1k1, I_2k2, ··· , I_MkM).

When a data object d_p is described by (x₁, x₂, ··· , x_M), the index (k₁, k₂, ··· , k_M) of its corresponding cell is determined as follows:

which means that we can easily locate the home cell of a data object via a simple arithmetic operation even in a high dimensional space. The neighboring cells are easily determined by the indices. The indices (I_1k1, I_2k2, ··· , I_MkM) of 1-distance cells for a cell (I_1k1, I_2k2, ··· , I_MkM) are determined as follows.

In a similar manner, the indices of s-distance cells are determined as follows.

An s-distance cell is a cell located at a grid distance s from the home cell.

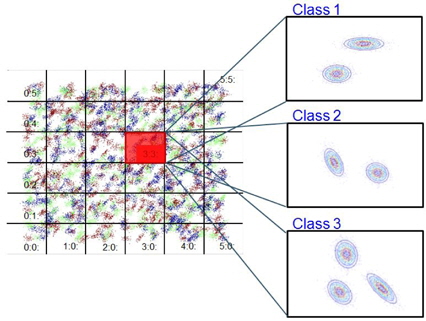
The proposed method models each grid as a mixture of Gaussians for each class. The constituent clusters are determined for each class using the k-means algorithm, which requires a pre-specified number of clusters. No information is available about how many clusters exist in a class of grids. Thus, a cluster validity index is used to determine the number of clusters. In a grid, a class usually has a small number of clusters, which might possibly be a single cluster.

Several cluster validity indices can be used to measure how well the clusters are formed [8, 20]. The R-squared (RS) index is a cluster validity index that measures the dissimilarity of clusters [20] as the degree of homogeneity between groups using values from 0 to 1, where 0 indicates that there is no difference among the clusters and 1 indicates that there are significant differences among the clusters. RS is defined as follows:

where

, where x_i is the i-th data point, is the mean of all the data, |D| is the overall data size, C_i is the i-cluster, is the centroid of the i-cluster, and N_c is the number of clusters. The RS index is always 0 for a dataset with a single cluster, and thus it is preferable to have more than one cluster.

In a mixture of Gaussian models, it is better to merge two neighboring clusters because small condensed Gaussian components can have biased effects on Bayesian inference. To measure the proximity of two clusters, we propose a so-called separability index Sp(i, j) for a pair of clusters C_i and C_j :

where rad_P (i) indicates the distance to the centroid of the cluster C_i for data where the distance from the centroid is ranked among the p percentages of the top distances, and d_ij is the distance between the cluster centroids of clusters i and j.

The following strategy is used to determine the number of clusters for each class in a grid:

procedure Determine_No._of_Clusters   For i = 2 to K do       Apply the k-means algorithm to the dataset with i clusters       Compute the RS index score RS(i) for the clustering results   end   Choose the number of clusters that yield the highest RS index score   For each pair of clusters among the selected number of clusters       Compute the separability index Sp(i, j) for the pair(Ci, Cj)       If the index score Sp(i, j) > the specified threshold θs           Merge the corresponding pair of clusters

Bayesian inference uses the Bayes’ rule to derive the posterior probability P(C|d) of a class C for the given data d as the product of the prior probability P(C) of class C and the likelihood P(d|C), which is the probability that class C generates the data d. The Bayes’ rule is represented as follows.

In the Bayesian-based classifier, a probability model is constructed for the likelihood function from the training dataset and the prior probability is determined for each class. When a data object d is given, the posterior probability for each class C is computed, and its class is assigned the class label with the highest posterior probability. In the Bayesian rule, the denominator P(d) is not evaluated because it applies to each posterior computation, and thus it does not affect the determination of the class label with the highest posterior probability.

The proposed method models the probability distributions of the classes for each cell. The probability distributions are assumed to be Gaussian. Gaussian distributions can be specified by the mean and covariance matrix. The method keeps track of the sufficient statistics required for the Gaussian distributions, i.e., the numbers of data objects, sums of the attribute values, and squared sums of the attribute values for each class. To consider the correlations between attribute variables, we must maintain the sums of the products for each pair of attribute variables. Let N_ij be the size of the data subset D_ij that belongs to class C_j in cell G_i , where M_ij is the sum of the attribute values of data subset D_ij and S_ij,pq is the sum of the products of the p-th and q-th attribute values of the data subset D_ij. After obtaining the sufficient statistics, the mean m_ij and covariance matrix ∑_ij for D_ij are computed as follows.

The sufficient statistics-based method can acquire statistical information during a single scan of the dataset, which can be updated incrementally when additional data objects are available due to the additive property of the sufficient statistics.

The following MapReduce operations are used to obtain the sufficient statistics for the mean and covariance matrix of the attribute values. The map function assumes that the first element of the input records is the class label and that the remaining elements are attribute values listed in a specific order. First, the map function finds the index k₁k₂ ··· k_M of the grid cell occupied by the data R using Eq. (4). Next, it generates a list where the element ‘1’ indicates the count of records, the elements from the second place to the (M+1)-th place contain the attribute values as they appear in the data R, and the pairwise products of the attribute values are appended to the end of the list.

procedure: map(key = null, value = record R)   L[ ] := splits(R)   Compute the index k1k2 ··· kM of the data that correspond to L[2..M + 1]       Using Eq. (4)   V al := ‘1’   For i := 2 to M + 1       V al := V al + “ ” + L[i]   For i : = 2 to M + 1       For j:= i to M + 1       V al := V al + “ ” + L[i] ∗ L[j]   write((k1k2 ··· kM,L[1]), V al)

The reduce function aggregates all of the records that belong to the same cell by adding them in a position-wise manner. The output generated by the function comprises the key-value pair(s), where key is the index for the corresponding grid cell, and value comprises the class label, the list of means, and the upper triangular portion of the covariance matrix.

procedure: reduce(key = (k1k2 ··· kM, class), values)   count := 0   Sum[1..M] := 0   V ar[1..(M(M + 1)/2)] := 0   Foreach val in values       L[ ] = splits(val)       count := count + L[1]       For i : = 1 to M         Sum[i] = L[i+1]       For i : = 1 to M         For j := i + 1 to M           V ar[i ∗ (i − 1)/2 + j] := V ar[i ∗ (i − 1)/2 + j] + L[i ∗ (i − 1)/2 + j + M + 1]   Mean[1..M] := 0   for i : = 1 to M       Mean[i] := Sum[i]/count   Cov[1..M][1..M] = 0   For i := 1 to M       For j := i + 1 to M         Cov[i][j] := V ar[i ∗ (i − 1)/2 + j]/(count − 1)   For i := 1 to M       For j := i to M         Cov[i][j] := Cov[i][j] − Mean[i] ∗ Mean[j]   V al := class + “ ” + count   For i : = 1 to M       V al := V al + “ ” + Mean[i]   For i : = 1 to M       For j := i to M         V al := V al + “ ” + Cov[i][j]   Write(k1k2 ··· kM, V al))

The map function produces an extended record, which is M²/2 + 3M/2 times the original size M. This may impose a large burden when handling the intermediate files between map processes and reduce processes. To handle this problem, we apply the combine function after the map processes and before the reduce processes. The combine processes run on every node that runs the map processes. The input for the combine process comprises all of the data generated by the map processes on a given node. The output from the combine processes is then sent to the designated reduce processes. The proposed method uses the reduce function as the combine function because their roles are similar, except for the computation of the model parameters such as the means and covariances. Using the combine function dramatically reduces the bandwidth usage and the size of the intermediate files.

procedure: combine(key = (k1k2 ··· kM, class), values)   count := 0   Sum[1..M] := 0   V ar[1..(M(M + 1)/2)] := 0   Foreach val in values       L[ ] = splits(val)       count := count + L[1]       For i : = 1 to M         Sum[i] = L[i+1]       For i : = 1 to M         For j := i + 1 to M           V ar[i ∗ (i − 1)/2 + j] := V ar[i ∗ (i − 1)/2 + j] + L[i ∗ (i − 1)/2 + j + M + 1]   V al := count   For i : = 1 to M       V al := V al + “ ” + Sum[i]   For i : = 1 to M       For j := i + 1 to M         V al := V al + “ ” + V ar[i]   Write(key, V al))

To classify a new query data, the proposed method uses the Bayesian inference rule. The MapReduce functions provide the model parameters for the Gaussian probability distributions of the classes in each grid cell. Each cell maintains the model parameters for the probability distributions of the classes. We refer to the cell that contains the query data as the home cell G_h. Let NB_h be the index set of neighboring cells and d(G_i, G_h) is the distance of a cell G_i from the home cell G_h. d(G_i, G_h) = s if G_i is an s-distance cell from G_h.

The prior probability of class C_k in cell G_i is defined as follows.

The likelihood P_i(d_p|C_k) of data d_p in class C_k at grid G_i is defined as follows.

The posterior probability P_i(C_k|d_p) of class C_k for data d_p is given as follows.

The denominator P_i(d_p) is the same for all classes C_k at G_i. Thus, we can compute the posterior probability without using P_i(d_p), as follows.

The probability support of class C_k to d_p is accumulated as follows:

where (d(G_n,G_h)+1)^w is a weighting factor that makes closer cells contribute more to class determination and w(w > 0) is a control factor that determines the level of contribution. The scope of the neighbors can be controlled by fixing the maximum grid distance s from the home cell to the neighboring cells.

The final probability P(C_k|d_p) is determined by computing the normalization of the probability supports, as follows.

The data object d_p is classified into the class C(d_p) with the maximum final probability:

The proposed algorithm was implemented using the MapReduce libraries in Hadoop. The programs developed were executed on a Hadoop cluster with eight commodity computers. To assess the applicability of the proposed method, we applied the method to a numeric benchmark dataset: Iris[10], which comprised 150 objects with four numeric attributes and three classes. A tenfold cross-validation was performed using the dataset. To determine the appropriate probability distributions, we required a sufficiently large dataset; thus, we enlarged the dataset by sampling new data and adding Gaussian noise to the attribute values in the existing dataset, thereby obtaining a training dataset of 10,000 objects. Each attribute domain was partitioned into five equidistant intervals. The number of cells was 625. The accuracy obtained in the experiment was comparable to that obtained with the C4.5 algorithm using Iris data with 150 data objects. We found that the proposed method performed adequately in the classification of big data. The use of the combine function dramatically reduced the volume of intermediate files, thereby making the reduce phase execute over two times faster.

Another artificial dataset with three attributes and three classes was generated randomly using 900 Gaussian distributions, where the centroids of the covariance matrices were selected randomly. For each Gaussian distribution, 500 data points were generated that formed a cluster in the space. In the experiments, the range of each attribute was partitioned into five intervals. A tenfold cross-validation was performed using the dataset. According to the experiments, the average accuracy was 94.3%.

In other experimental settings, we changed the number of partitions of the attributes from two to six. There was no significant change in the accuracy, but there was a trade-off between the execution time and the storage required to maintain sufficient statistics for the grids as the number of partitions changed. The increase in the number of partitions decreased the data volume handled by a single reducer and more reducers were instantiated, so the degree of parallelism was also increased. Because the reducers ran the k-means algorithm several times, the reduction in the data volume for each reducer improved the execution time significantly.

The merging of neighboring clusters using the separability index improved the accuracy considerably, as shown in Table 1. Thus, small condensed Gaussian distributions with small determinants in their covariance matrices had higher likelihoods for queries.

The MapReduce model is an efficient computational model for distributed parallel processing with big data. In this study, we proposed a grid-based Bayesian inference classification method that can handle big data.

The proposed method has the following advantages. It is a single-pass algorithm that does not require multiple scans of the training data to construct a classifier. It is very efficient at locating the neighbors because the home cell of a data query is determined by simple arithmetic computation and the neighboring cells are determined by index manipulation. It is scalable for big volumes of data because only the sufficient statistics for the probability distributions are maintained, which can be updated by simple arithmetic operations as data objects arrive. The neighboring class distribution can be visualized readily because the neighboring cells are easily located and their class probability distributions can be computed simply.

The proposed method has the following disadvantages. Fixed length interval-based partitioning of the data space might not capture the appropriate probability distributions of the classes. To mitigate this problem, we could decrease the interval lengths but there might be too many cells to be maintained in a highdimensional data space. A sufficiently large training dataset is required to ensure that each grid cell has sufficient data subsets to characterize the parameters of the probability distributions. The proposed approach is not appropriate for classification problems with small training sets but it works well for big data. The costly k-means clustering algorithm is executed multiple times on each grid. As the number of grids increase, the volume of data handled by a reducer decreases and the processing time on a reducer also declines. This problem can be resolved by increasing the size of the Hadoop clusters. Further improvements can be achieved by employing a sampling technique that uses a subset of the dataset to determine the number of clusters and their centroids and covariance matrices, before collecting the sufficient statistics for the corresponding clusters with respect to the overall dataset.

Our experiments showed that the proposed system performed well as a classifier for big data. Thus, the method could be used for solving big data classification problems. In future research, we aim to extend the proposed method to the simultaneous handling of datasets with both categorical and numerical attributes.