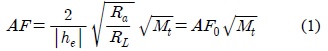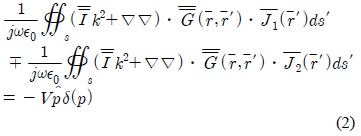논문은 하이브리드 발룬을 갖는 계산가능 다이폴안테나가 접지판 위에 수평 및 수직으로 놓여 있을 경우의 안테나 인자 특성을 모멘트법으로 검토하고 있다. 안테나 인자의 표현식은 전력부정합손실의 개념을 적용하여 도출한 식을 사용하였으며, 안테나 인자의 계산에서 나타나는 안테나의 입력 임피던스 및 유효길이는 모멘트법을 적용하여 계산하고 있다. 그 결과, 접지판 위에서의 안테나 인자 특성은 안테나의 편파상태에 따라 달라지며 자유공간 안테나 인자와는 최대 ± 0.14 dB 의 차이가 발생함을 알 수 있었다. 또한, 수평편파인 경우의 안테나 인자 변동폭이 수직편파인 경우보다 0.2 dB 정도 더 크다는 것도 확인할 수 있었다.
This paper presents the antenna factor characteristics of a calculable dipole antenna with a hybrid balun, installed above ground plane vertically and horizontally, using Method of Moments (MoM). An expression for the antenna factor is formulated using the concept of power mismatch loss. The input impedance and effective length of the antenna, which are in the formula of the antenna factor, are calculated using the MoM. The results show that the antenna factors above a ground plane are agreed with the free space antenna factors within ± 0.14 dB. The horizontal antenna factors are varied more by 0.2 dB than the vertical antenna factors.
30∼1000 MHz의 주파수 대역에서 사용하는 Roberts 발룬을 내장한 다이폴안테나는 ANSI 규격에 제시되어 있으나[1], 최근에는 계산가능 다이폴안테나 (calculable dipole antenna)가 제안되어 안테나 인자의 교정과 안테나시험장 또는 EMC 시험 야외시험장의 적합성 평가에 사용된다[2]. 이러한 계산가능 다이폴안테나에 대한 연구는 30∼1000 MHz의 주파수 대역에 걸쳐 안테나 인자의 교정 및 안테나시험장 평가용으로 보고되고 있다[2-10]. 하이브리드 발룬을 내장한 계산가능 표준 다이폴안테나는 4개의 다이폴안테나를 사용한 30∼1000 MHz 주파수 대역용 표준 안테나가 보고되어 있으며[4,5], 850 MHz∼2.2 GHz 주파수 대역용[6] 및 1∼3 GHz 주파수 대역용[7,8]뿐만 아니라, 3개의 안테나 A (1∼2 GHz),B (2∼4 GHz),C (4∼6 GHz)를 사용하여 1∼6 GHz의 주파수 대역을 커버하기 위한 계산가능 다이폴안테나도 보고되어 있다[9]. 30 MHz∼2 GHz대역을 커버하기 위해 광대역 발룬을 사용한 계산가능 다이폴안테나[11] 및 다이폴 안테나의 안테나 인자에 대한 불확도 산출에 관한 연구도 보고되어 있다[12].
계산가능한 다이폴안테나의 기본 개념은 문헌[8]에서 언급한 바와 같이, 안테나 소자를 제외한 balun 부분의 S-파라미터 측정결과를 안테나 소자에 대한 이론계산 결과 (입력 임피던스, 유효길이)와 결합하여 안테나의 특성 (안테나 인자)을 결정하는 것이다.
이와 같은 계산가능 다이폴안테나의 안테나 인자에 대한 이론해석과 실험적 연구는 영국의 측정표준기관인 NPL (National Physical Laboratory)을 중심으로[3-6] 많은 연구자들에 의해 연구되고 있다. 자유공간에서 공진하도록 설계된 다이폴안테나를 무한히 넓은 접지판 위에서 사용하게 되면 안테나 높이에 따라서 안테나의 급전점 임피던스가 변하게 되어 안테나 인자도 변한다. 즉, 접지판 위의 안테나 인자는 자유공간 안테나 인자와는 다른 값을 가지게 된다. 실제로 야외시험장에서 EMC 시험을 실시할 때에는 접지판 위에서 시험하도록 규정하고 있으므로 측정용 EMC 안테나는 접지판 위에서 사용하게 된다.
이 경우에는 EMC 안테나가 접지판과의 결합에 의한 영향뿐만 아니라 EUT와의 결합에 의한 영향도 동시에 받게 된다. 또한, 야외시험장의 적합성을 평가할 때에는 자유공간에서 설계된 다이폴안테나가 접지판 위의 송수신 위치에 각각 놓이므로 접지판 및 안테나 간의 상호결합에 의해 송·수신 안테나의 안테나 인자는 변하게 된다.
본 논문에서는 자유공간에서 설계된 계산가능 다이폴안테나가 접지판 위에 놓여질 때 접지판 위에서 안테나 인자가 어떻게 변하는지를 수평편파 및 수직편파에 대하여 모멘트법 (MoM, Method of Moments)을 적용하여 계산한 결과를 비교 검토하였다. 그 결과, 접지판 위에서의 안테나 인자 특성은 안테나의 편파상태 (수평편파 및 수직편파)에 따라 달라지며 자유공간 안테나 인자와는 최대 ± 0.14 dB 의 차이가 발생함을 알 수 있었다. 이론해석의 타당성을 검증하기 위해 실험결과와도 비교하였다.
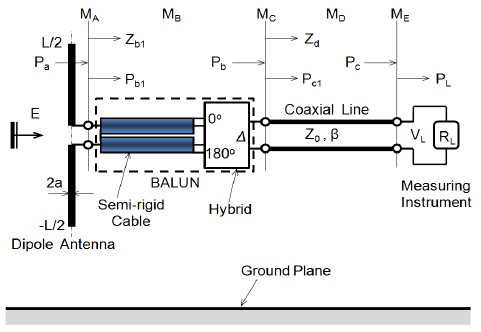
그림 1은 접지판 위에 놓여진 하이브리드 balun을 사용한 계산가능 다이폴 안테나의 구조를 나타낸다. 그림 1에서 보는 것처럼, 3 dB 180° 하이브리드 커플러는 입력단 (0° 단자와 180° 단자)과 출력단 (Δ 단자, Σ 단자는 50 Ω으로 종단함)으로 구성되며, 안테나 소자에서 하이브리드의 입력단까지는 50 Ω 동축 케이블 (semirigid coaxial cable)을 이용하여 연결한다. 동축 케이블과 하이브리드 커플러의 입력단 사이에는 3 dB pad가 삽입되어 있으며, 하이브리드 커플러 출력단의 Δ 단자는 동축 케이블 (coaxial line)을 통하여 측정기와 연결되어 있다.
그림 1에서 보는 것처럼, balun은 다이폴 소자의 급전부에서 하이브리드 커플러의 Δ 단자까지이며, 위상 정합된 2개의 동축 케이블과 2개의 50 Ω 3 dB pad, 3 dB 180° 하이브리드 커플러 (50 Ω이 연결된 Σ 단자는 내장되어 있음)로 구성된다.
본 논문에서 사용한 하이브리드 커플러는 3개의 외부 단자로 구성 (50 Ω이 연결된 Σ 단자는 내장되어 있음)된 Picosecond Pulse Labs, Inc.사의 Model 5310A-104 Phase-Matched Balun (4 MHz∼6.5 GHz)을 사용하였다[15].
그림 1에서 안테나 소자에 입사하는 전기장의 세기
여기서,
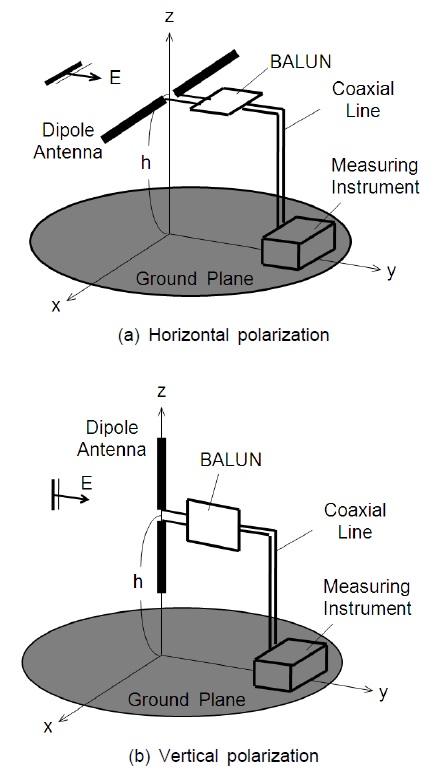
그림 2와 같은 접지판 위의 수평 및 수직 다이폴안테나의 중앙에서 전압 V로 급전하면 전류분포에 관한 적분 방정식은 각각 다음과 같이 주어진다.
여기서, 는 단위 다이애딕, 는 Dirac의 델타함수,
전류분포에 관한 적분방정식 (2)의 해는 구분적정현 함수를 사용한 Galerkin의 모멘트법으로 해석하였으며[14], 구체적인 정식화 과정의 기술은 생략하기로 한다. 안테나인자를 계산하기 위해서는 다이폴안테나의 입력 임피던스뿐만 아니라, 유효길이도 계산하여야 한다[8]. 또한, 본 논문의 계산에 사용한 안테나는 자유공간에서 공진하는 반파장 공진 다이폴 안테나를 사용하였다[7].
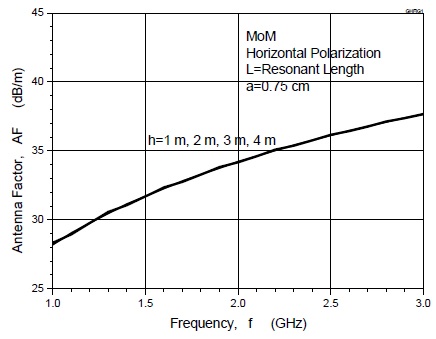
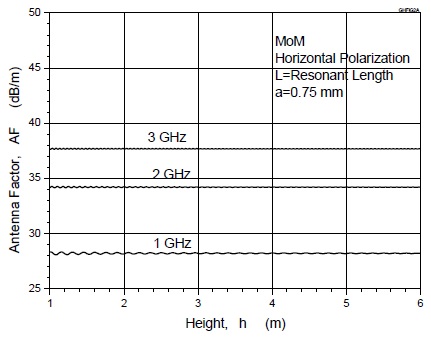
그림 3 및 그림 4는 접지판 위에 놓인 수평 다이폴안테나의 안테나 인자를 모멘트법으로 계산한 결과를 나타낸다. 그림 3으로부터 알 수 있는 것처럼, 안테나 높이가 h=1 m, 2 m, 3 m, 4 m에서 계산한 안테나 인자의 주파수 특성은 거의 같은 값을 가진다. 또한, 그림 4에서 보는 것처럼, 접지판 위의 안테나 높이에 따라서 안테나 인자는 주기적으로 변동하는 특성을 가지는데 변동의 폭은 최대 0.28 dB (주파수 1 GHz의 1 m에서 최대 변동폭을 가짐)이내로서 매우 작다는 것을 알 수 있다.
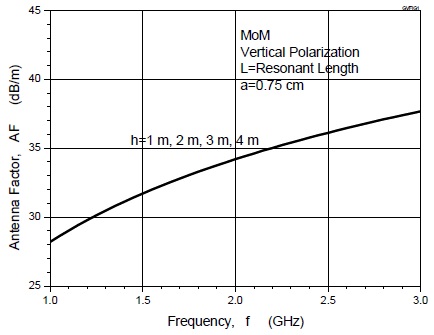
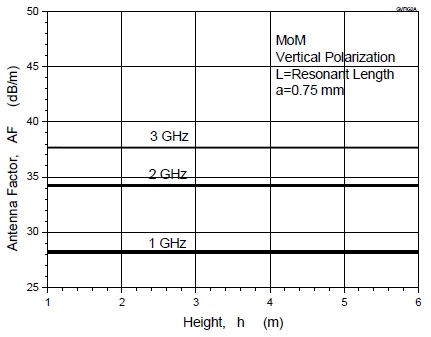
그림 5 및 그림 6은 접지판 위에 놓인 수직 다이폴안테나의 안테나 인자를 모멘트법으로 계산한 결과를 나타낸다. 그림 5로부터 알 수 있는 것처럼, 안테나 높이가 h=1 m, 2 m, 3 m, 4 m에서 계산한 안테나 인자의 주파수 특성은 수평편파의 경우와 마찬가지로 거의 같은 값을 가진다.
또한, 그림 6에서 보는 것처럼, 접지판 위의 안테나 높이에 따라서 안테나 인자는 주기적으로 변동하는 특성을 가지는데 변동의 폭은 최대 0.11 dB (주파수 1 GHz의 1 m에서 최대 변동폭을 가짐)이내로서 무시할 수 있을 정도로 작다는 것을 알 수 있다.
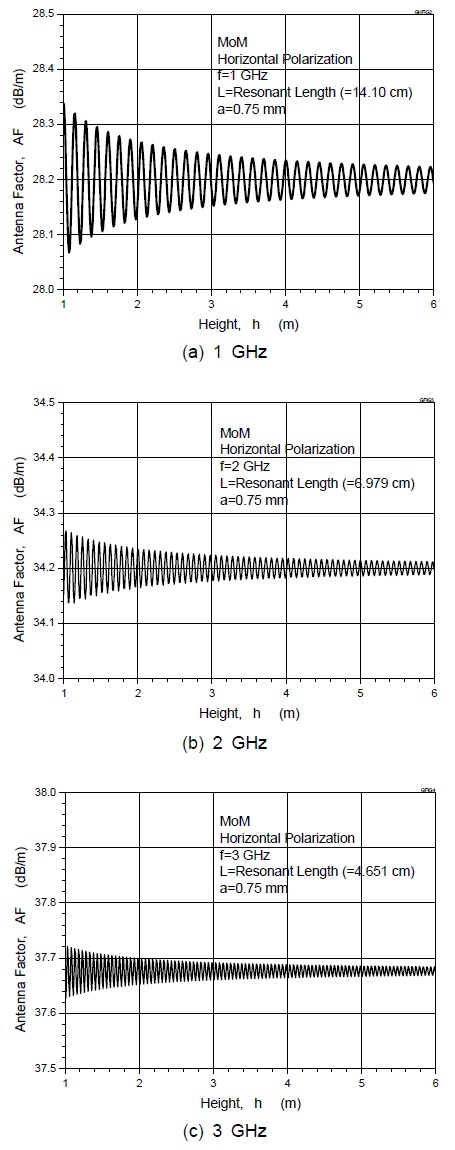
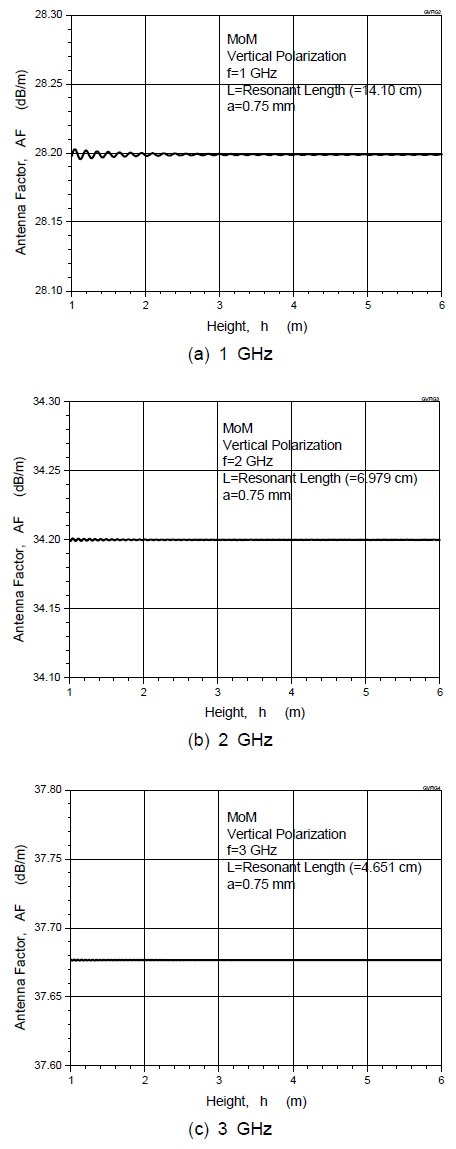
그림 4 및 그림 6에 나타낸 안테나 인자의 높이 특성은 안테나 높이에 따라서 주기적으로 변하는 특성을 가지는데 그림 4 및 그림 6에서는 구체적인 변화 양상이 잘 나타나 있지 않다. 안테나 높이에 따른 안테나 인자의 변화를 구체적으로 파악하기 위하여 수평편파에 대해서는 그림 7에, 수직편파에 대해서는 그림 8에 자세한 변화 특성을 나타내었다.
그림 7 및 그림 8에서 알 수 있는 것처럼, 접지판 위에서는 안테나 인자가 주기적으로 변하며 접지판에서 멀어질수록 (높이가 높아질수록) 자유공간 안테나 인자에 수렴하게 된다. 접지판 위에서 안테나 인자가 주기적으로 변하는 것은 안테나의 입력 임피던스가 주기적으로 변화하기 때문이다.
그림 7 및 그림 8에서 알 수 있는 것처럼, 접지판 위에 수평으로 놓여진 다이폴안테나 (수평편파)는 수직으로 놓여진 안테나 (수직편파)보다 접지판과의 결합이 강하므로 수평편파인 경우의 안테나 인자 변동폭이 수직편파인 경우보다 0.2 dB 정도 더 크다.
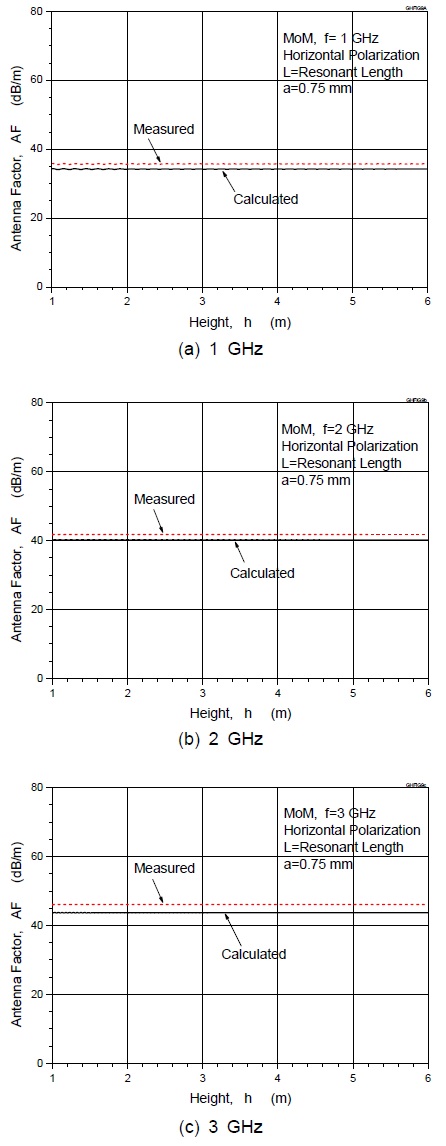
그림 9는 안테나 발룬의 산란행렬 측정값을 사용하여 구한 안테나 인자의 높이 특성을 나타낸다. 그림 9의 이론 계산값은 이상적인 발룬을 사용한 경우의 접지판 위에서의 안테나 인자이며, 산란행렬 측정값을 사용한 안테나 인자와도 그 경향이 잘 일치하고 있음을 알 수 있다. 그림 9에는 1 GHz, 2 GHz, 3 GHz의 3가지 주파수에 대하여 나타내었으며, 안테나 높이에 대한 주기적 감쇠진동의 모양 (그림 7 참조)은 안테나 인자의 다이나믹 레인지를 작게 하면 확인할 수 있다. 본 논문에서는 3가지의 주파수 전체를 비교하기 위하여 다이나믹 레인지를 크게 하였기 때문에 주기적 진동의 모양은 직선의 형태를 보이고 있다.
자유공간에서 설계된 다이폴안테나가 접지판 위에 수평 또는 수직으로 놓여 지면 안테나 인자의 특성이 변하게 되는데, 본 논문에서는 접지판 위의 안테나 높이에 따른 안테나 인자의 변화 특성을 모멘트법으로 검토하였다. 그 결과, 안테나 높이에 따라 안테나 인자는 주기적인 변동을 하며 수평편파인 경우의 변동폭은 0.28 dB이내이며, 수직편파인 경우의 변동폭은 0.11 dB 이내임을 알 수 있었다. 안테나 높이가 접지판에서 멀어질수록 안테나 인자는 자유공간 안테나 인자로 수렴함을 확인할 수 있었다. 또한, 수평편파는 수직편파보다 접지판과의 결합이 강하므로 수평편파인 경우의 안테나 인자 변동폭이 수직편파인 경우보다 0.2 dB 정도 더 크다는 것도 확인할 수 있었다.