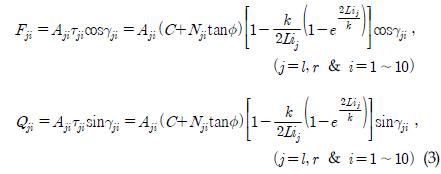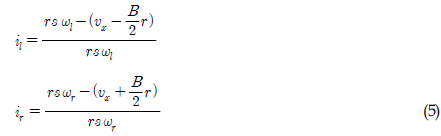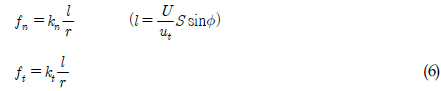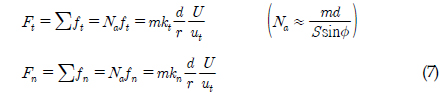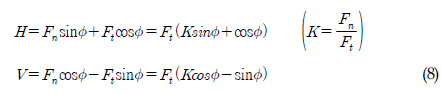해저플랜트 및 해양영토 확대와 무한한 자원의 보고인 해양을 개발하기 위한 수중건설 시장의 증가로 인해 해양의 열악한 입지조건에도 불구하고 더욱 다양한 형태의 해저작업이 필요하게 되었다. 이 때 수중에서의 구조물을 효율적으로 건설할 수 있는 장비인 수중건설용 로봇을 필요로 한다. 특히 다양한 해양플랜트 및 해양구조물을 잇는 해저 광통신 케이블, 전력 케이블 및 파이프라인을 해저에 매설하는 작업의 경우 주로 점착성이 강하거나 단단한 해저지반에서 이루어진다. 이 때 Trenching cutter, Water jet등을 이용한 매설작업 시 발생하는 반력을 견디기 위한 견인력과 기동성능을 얻는데 있어 트랙방식의 궤도차량이 큰 장점을 가지고 있다.
이러한 궤도차량의 동적거동을 해석하기 위해 운동 모델링과 수치 시뮬레이션 대한 연구가 많이 진행되어 왔다(Baladi and Rohani, 1979; Kim et al., 2004; Le et al., 1997; Murakami et al., 1992; Wong, 1993). 특히, Kim et al.(2004)는 궤도차량의 동적거동 해석에 있어 Murakami et al.(1992)에 의해 제안된 강체차량 모델과 다물체 동역학 해석 프로그램을 이용하여 모델링된 다물체 차량 모델의 동역학 해석결과들을 비교하는 연구를 수행하였다.
본 논문에서는 Baladi and Rohani(1979), Wong(1993) 그리고 Malcolm(1978)의 연구결과를 바탕으로 수중건설용 트랙기반 작업용 로봇의 차체인 궤도차량의 운동 모델링과 작업용 툴인 Trenching cutter의 모델링을 수행하고, 시뮬레이션을 통한 좌, 우 궤도의 속도에 따른 직진 및 선회운동, 그리고 Trenching 작업 시 궤도차량의 필요 견인력을 해석하고자 한다.
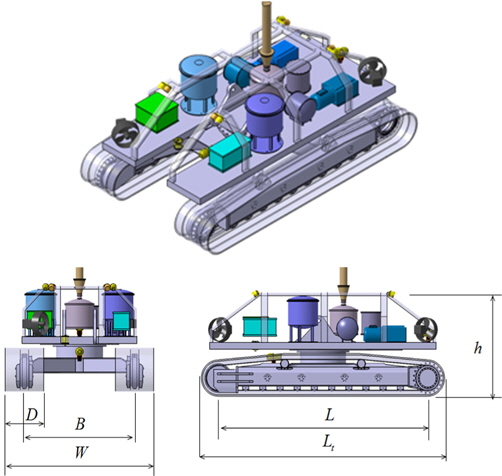
본 논문의 궤도차량 모델은 수중건설로봇사업단(후기 참고)에서 개발 중인 트랙기반 해저 중작업용 로봇이며 외형은 Fig. 1의 개념설계도와 같으며, 하부는 좌, 우 궤도가 있으며 상부프레임에는 내압용기, 케이블 연결부, 수중 추진기 그리고 작업용 툴 브래킷으로 구성되어 있다. 또한 주요부의 치수와 기호는 Table 1과 Fig. 1에 나타낸 바와 같다(Lee et al., 2015).
[Table 1] Specifications of the tracked vehicle model

Specifications of the tracked vehicle model
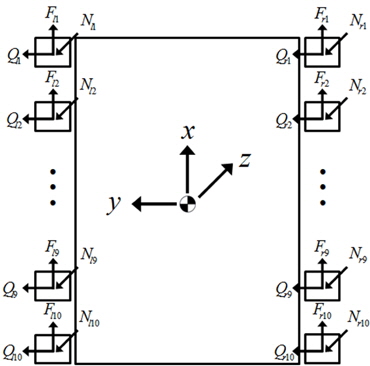
Fig. 2는 궤도차량의 차량고정좌표계와 각각의 궤도요소들과 지면사이에 작용하는 직진방향, 횡방향 그리고 수직방향의 힘들을 나타내었고, 차량고정좌표계의 원점은 차량의 기하학적 중심에 위치하도록 하고, 차량의 진행방향을 x축 그리고 z축을 연직 위 방향으로 하였으며, y축은 오른손법칙에 의하여 결정하였다(Lee et al., 2015). 이때 각각의 Surge, Sway, Yaw방향의 3 자유도 운동방정식은 식 (1)과 같다.
여기서
여기서
Wong(1993)은 궤도차량의 직진, 횡방향의 전단력을 아래 식(3)과 같이 궤도 슬립과 지면의 특성 그리고 수직응력의 함수로 제안하였다.
여기서
좌, 우 트랙의 스프라켓(Sprocket) 각속도를
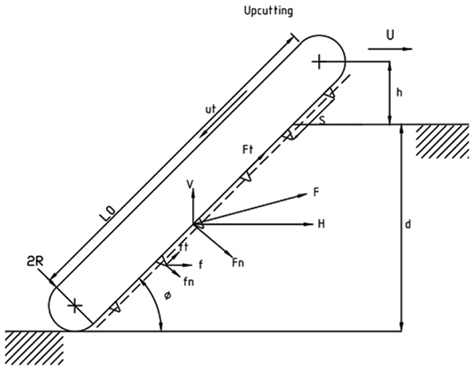
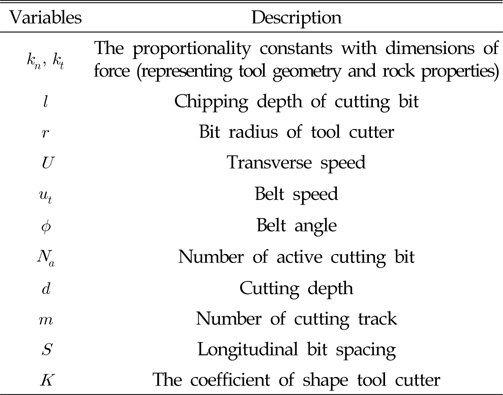
궤도차량에 부착되어 해저케이블 매설을 위해 해저 바닥을 파내는데 사용하는 작업용 툴을 Trenching cutter 또는 Trencher라고 하며, Fig. 3은 Trenching 작업 시 Cutter bar와 토양사이에서 발생하는 힘들을 나타내고 있으며, 이때 Trencher 모델에서 사용된 변수들은 Table 2와 같다.
[Table 2] Definition of variables
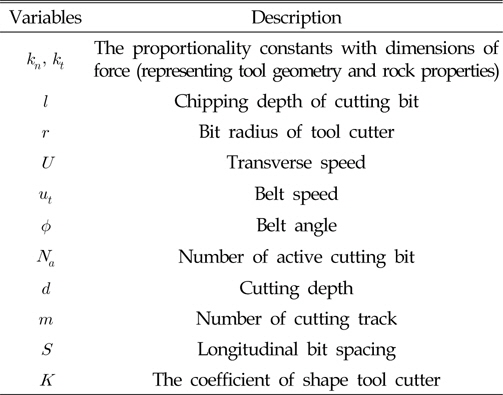
Definition of variables
Fig. 3 으로부터 Trencher의 각각의 Bit와 토양과의 경계면에서의 발생하는 수직, 수평방향의 힘은 식 (6)과 같이 나타 낼 수 있다.
이때 각각의 Tip에서 발생하는 힘의 합력을 구하면 아래 식(7)에 의해 툴과 토양의 경계면에서의 수평, 수직방향의 힘을 구할 수 있다(Malcolm, 1978).
또한, 궤도차량의 차량고정좌표계의
모델링된 궤도차량의 운동방정식과 Trencher 모델의 수치 시뮬레이션을 수행하여 동적거동을 확인하였다. 이때 사용된 시뮬레이션 프로그램은 Matlab/Simulink를 이용하였다. 수치 시뮬레이션에 사용된 입력은 좌, 우 궤도의 스프라켓 회전속도이며 노면은 경사가 없으며 장애물 및 굴곡이 없는 평탄한 지형 그리고 토양의 재질은 Dense sand로 가정하였다.
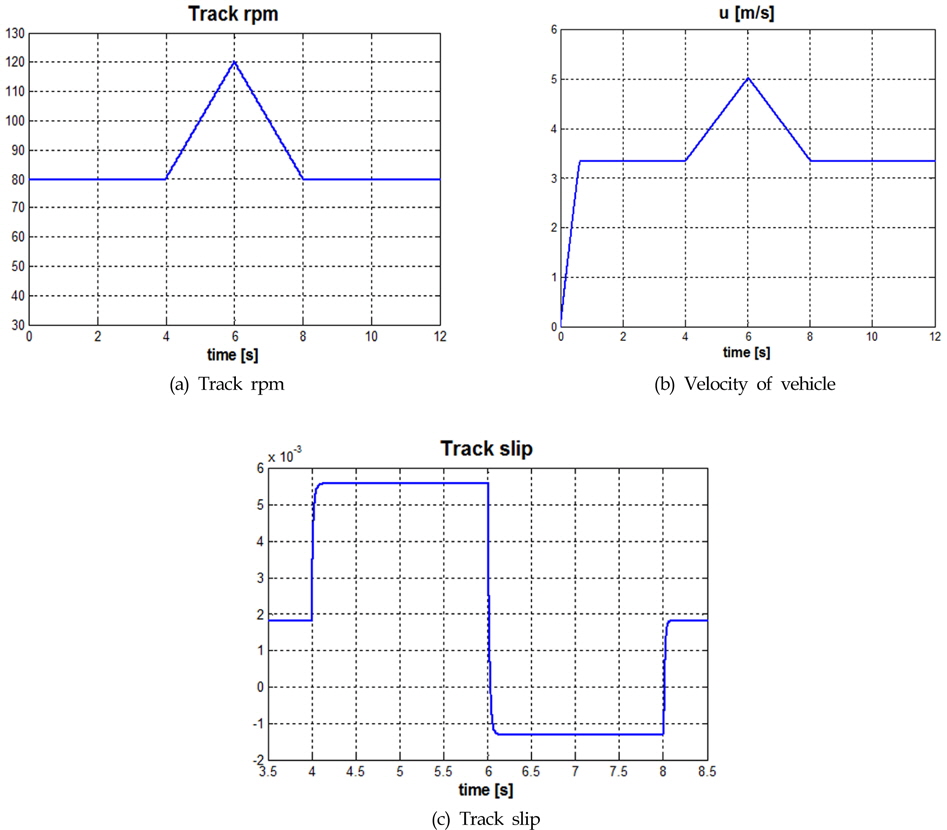
직진주행 시뮬레이션의 경우 양쪽 궤도의 입력은 Fig. 5 (a)에서처럼 초기 80rpm으로 시작하여 4~8초 구간에서는 120rpm으로 증가 후 다시 80rpm으로 감소시켰다. 이때 Fig. 5 (b)와 같이 초기 차량의 속도가 0m/s으로 시작하여 약 0.6초에 3.3m/s로 등속운동을 하다 궤도의 입력이 변하는 구간(6초~8초)에서 가속 및 감속운동을 하는 것을 볼 수 있다. 또한, Fig. 5 (c)의 그래프에서 시간에 따른 궤도 슬립의 변화를 보면 궤도입력에 따라 식 (4)와 식 (5)에 의해 가속구간(4초~6초)에서는 궤도차량의 속도에 비해 궤도가 빠르게 회전하므로 슬립이 증가하고 감속구간(6초~8초)에서는 반대의 현상이 일어남을 알 수 있다.
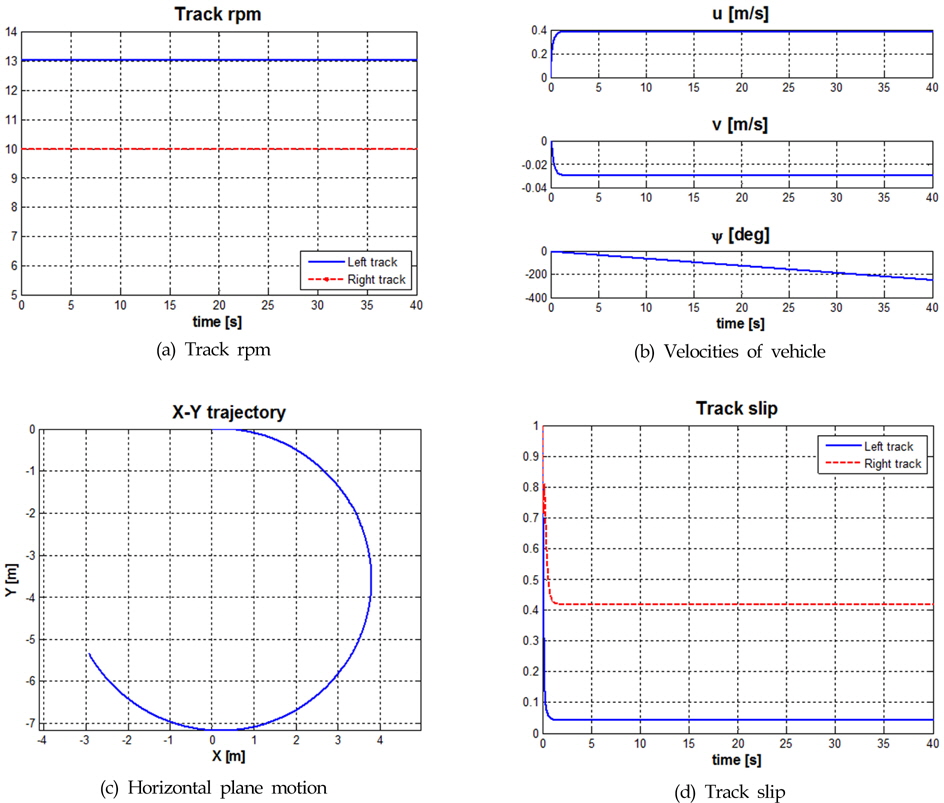
선회운동 시뮬레이션의 경우 양쪽 궤도의 입력은 Fig. 6 (a)에서처럼 좌, 우 궤도의 회전속도를 각각 13, 10rpm을 설정하였다. 이때 직진주행과는 다르게 좌, 우 궤도의 속도차이에 따른 횡방향의 속도와 방향각이 생김을 Fig. 6 (b)를 통해 알 수 있고, 그에 따른 미끄럼 조향을 하여 Fig. 6 (c)와 같이 선회운동이 이루어짐을 확인 할 수 있다. Fig. 6 (d)는 그때의 좌, 우 궤도의 슬립을 나타낸다.
Trenching 작업 시 주행 시뮬레이션의 경우 개념설계상 설정해 둔 운용 목표인 최고 주행속도 2km/h(0.56m/s)와 Trenching 작업 시 최대 작업 속도인 300m/h(0.08m/s)을 가지도록 궤도 회전속도를 조절하여 시뮬레이션을 수행하였다. 이때 Trenching cutter bar의 회전각도
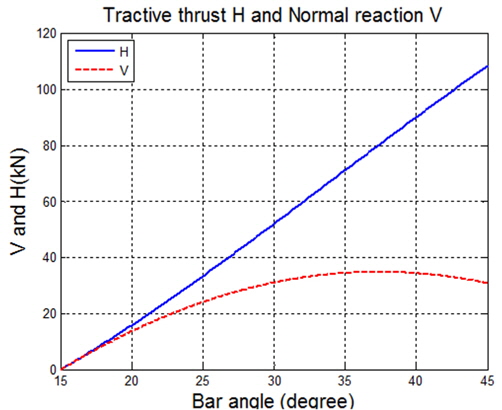
이때 시뮬레이션 결과는 Table 3에서 나타낸 바와 같고, 툴의 각도가 15°에서부터 지면과 맞닿기 시작하므로 그때의 수평, 수직방향의 반력은 0이다. 또한 툴의 각도가 증가할수록 Trencher와 지면과 닿는 면적이 증가함에 따라 생기는 반력도 증가하므로 궤도 스프라켓에서 필요 토크 또한 증가함을 알 수 있다. 이때 토크는 궤도 슬립에 의해 발생하는 직진방향의 전단력과 궤도 스프라켓의 반경에 의해 구할 수 있다.
[Table 3] Simulation of linear motion on trenching

Simulation of linear motion on trenching
본 논문에서는 트랙기반 해저 중작업용 수중로봇의 하부프레임인 궤도차량의 운동 모델링 및 작업용 툴인 Trencher의 모델링을 수행하였다. 모델링된 시스템의 동적거동 및 설계목표 성능을 확인하기 위하여 Matlab/Simulink 프로그램을 이용하여 수치 시뮬레이션을 수행하였다. 이를 통해 궤도가 회전함에 따라 토양과 궤도사이에서 생기는 전단력에 의해 차량이 주행하고, 선회운동의 경우 좌, 우 궤도의 속도차이에 의한 미끄럼 조향을 하는 것을 확인하였다. 또한, 설계목표인 Trenching 작업시 최대 속도로 운용할시 필요한 궤도 스프라켓의 최대 토크를 계산하였다.
궤도차량의 운동모델을 이용하여 운동성능해석은 물론 궤도차량의 자율이동을 위한 제어기 설계 모델로도 사용하고자 하며, Trencher의 모델을 이용하여 필요한 최대토크 계산을 함으로써 궤도차량과 Trencher를 구동하는데 필요한 구동모터 용량의 설계에 필요한 자료를 제공할 수가 있다.
향후 연구로는 토양모델을 해저지반과 유사한 물성치를 가지는 토양 또는 해저지반의 실험모델을 추가하고, 험지 및 경사로가 고려된 운동 모델링을 수행할 계획이다. 추가적으로 조류 및 여러 가지 외란이 발생하여도 Trenching 작업을 하면서 방향각을 유지할 수 있도록 하는 직진주행 알고리듬을 개발해 나갈 계획이다.