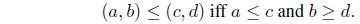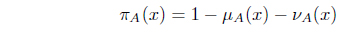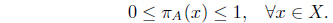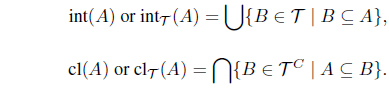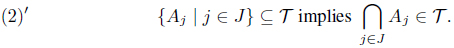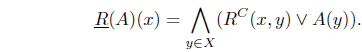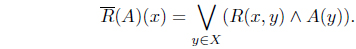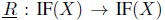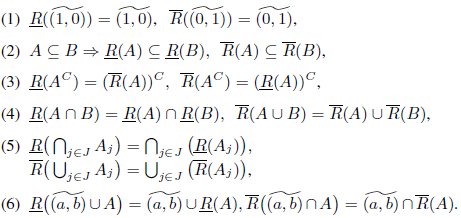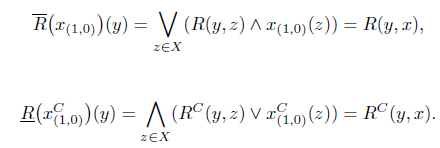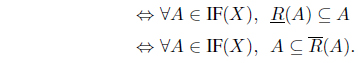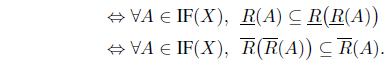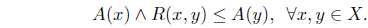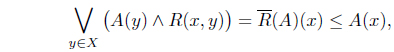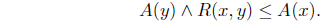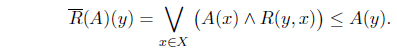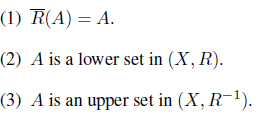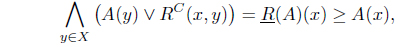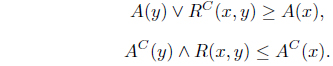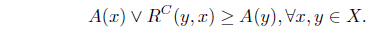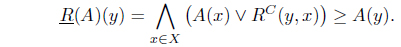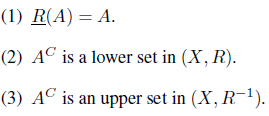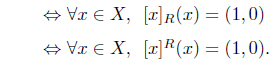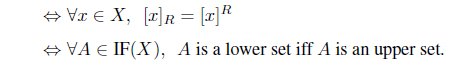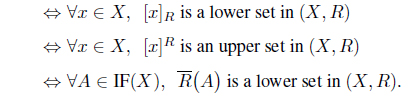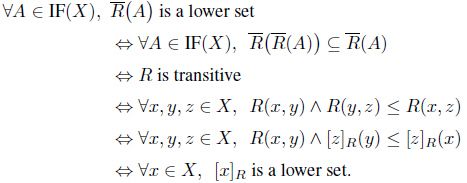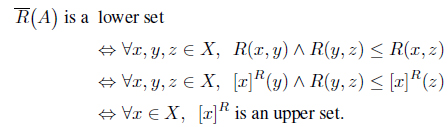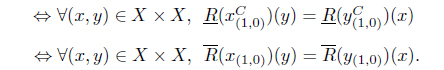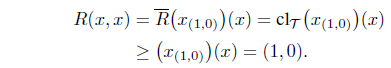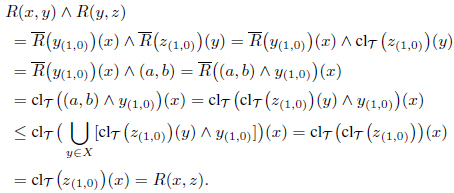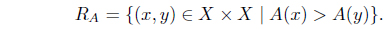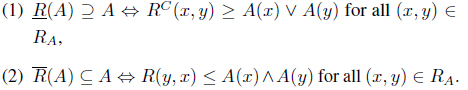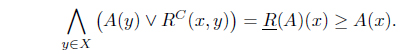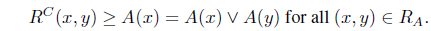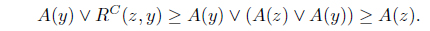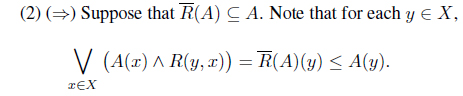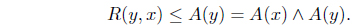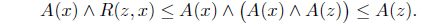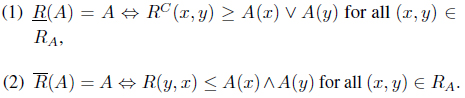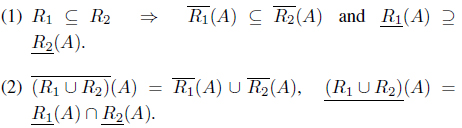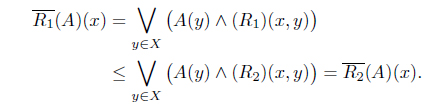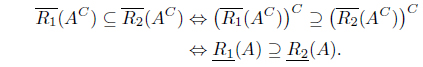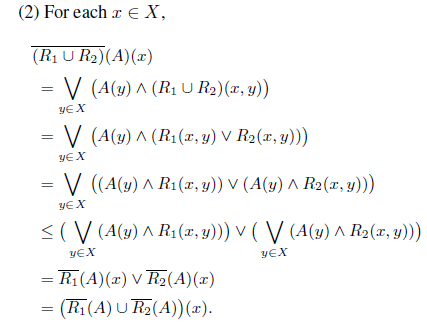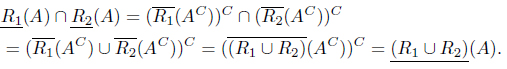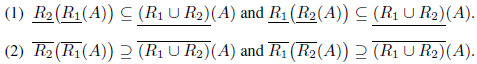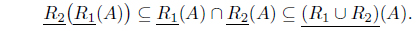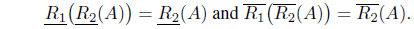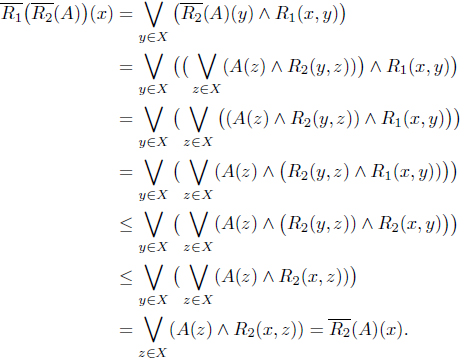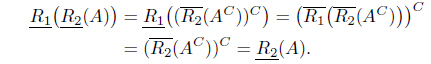A Chang’s fuzzy topology [1] is a crisp subfamily of fuzzy sets, and hence fuzziness in the notion of openness of a fuzzy set has not been considered, which seems to be a drawback in the process of fuzzification of the concept of topological spaces. In order to give fuzziness of the fuzzy sets, Çoker [2] introduced intuitionistic fuzzy topological spaces using the idea of intuitionistic fuzzy sets which was proposed by Atanassov [3]. Also Çoker and Demirci [4] defined intuitionistic fuzzy topological spaces in Šostak’s sense as a generalization of smooth topological spaces and intuitionistic fuzzy topological spaces. Since then, many researchers [5–9] investigated such intuitionistic fuzzy topological spaces.

On the other hand, the theory of rough sets was proposed by Z. Pawlak [10]. It is a new mathematical tool for the data reasoning, and it is an extension of set theory for the research of intelligent systems characterized by insufficient and incomplete informations. The fundamental structure of rough set theory is an approximation space. Based on rough set theory, upper and lower approximations could be induced. By using these approximations, knowledge hidden in information systems may be exposed and expressed in the form of decision rules(see [10, 11]). The concept of fuzzy rough sets was proposed by replacing crisp binary relations with fuzzy relations by Dubois and Prade [12]. The relations between fuzzy rough sets and fuzzy topological spaces have been studied in some papers [13–15].

The main interest of this paper is to investigate characteristic properties of intuitionistic fuzzy rough approximation operators and intuitionistic fuzzy relations by means of topology. We prove that the upper approximation of a set is the set itself if and only if the set is a lower set whenever the intuitionistic fuzzy relation is reflexive. Also we have the result that if an intuitionistic fuzzy upper approximation operator is a closure operator or an intuitionistic fuzzy lower approximation operator is an interior operator in the intuitionistic fuzzy topology, then the order is an preorder.

Let X be a nonempty set. An intuitionistic fuzzy set A is an ordered pair

where the functions 𝜇_A : X → I and 𝜈_A : X → I denote the degree of membership and the degree of nonmembership respectively and 𝜇_A + 𝜈_A ≤ 1(see [3]). Obviously, every fuzzy set 𝜇 in X is an intuitionistic fuzzy set of the form .

Throughout this paper, ‘IF’ stands for ‘intuitionistic fuzzy.’ I ⊗ I denotes the family of all intuitionistic fuzzy numbers (a, b) such that a, b ∈ [0, 1] and a + b ≤ 1, with the order relation defined by

For any IF set A = (𝜇_A, 𝜈_A) of X, the value

is called an indeterminancy degree(or hesitancy degree) of 𝑥 to A(see [3]). Szmidt and Kacprzyk call 𝜋_A(𝑥) an intuitionistic index of 𝑥 in A(see [16]). Obviously

Note 𝜋_A(𝑥) = 0 iff 𝜈_A(𝑥) = 1 – 𝜇_A(𝑥). Hence any fuzzy set 𝜇_A can be regarded as an IF set (𝜇_A, 𝜈_A) with 𝜋_A = 0.

IF(X) denotes the family of all intuitionistic fuzzy sets in X, and cIF(X) denotes the family of all intuitionistic fuzzy sets in X with constant hesitancy degree, i.e., if A ∈ cIF(X), then 𝜋_A = c for some constant c ∈ [0, 1). When we process basic operations on IF(X), we do as in [3].

Definition 2.1. ( [2, 17]) Any subfamily of IF(X) is called an intuitionistic fuzzy topology on X in the sense of Lowen ([18]), if

(1) for each (a, b) ∈ I ⊗ I, , (2) A, B ∈ implies A ᑎ B ∈ , (3) {Aj ∣ j ∈ J} ⊆ implies ∪j∈J Aj ∈ .

The pair (X, ) is called an intuitionistic fuzzy topological space. Every member of is called an intuitionistic fuzzy open set in X. Its complement is called an intuitionistic fuzzy closed set in X. We denote . The interior and closure of A denoted by int(A) and cl(A) respectively for each A ∈ IF(X) are defined as follows:

An IF topology is called an Alexandrov topology [19] if (2) in Definition 2.1 is replaced by

Definition 2.2. ( [20]) An IF set R on X × X is called an intuitionistic fuzzy relation on X. Moreover, R is called

(i) reflexive if R(𝑥, 𝑥) = (1, 0) for all 𝑥 ∈ X, (ii) symmetric if R(𝑥, 𝓎) = R(𝓎, 𝑥) for all 𝑥, 𝓎 ∈ X, (iii) transitive if R(𝑥, 𝓎) Λ R(𝓎, z) ≤ R(𝑥, z) for all 𝑥, 𝓎, z ∈ X,

A reflexive and transitive IF relation is called an intuitionistic fuzzy preorder. A symmetric IF preorder is called an intuitionistic fuzzy equivalence. An IF preorder on X is called an intuitionistic fuzzy partial order if for any 𝑥, 𝓎 ∈ X, R(𝑥, 𝓎) = R(𝓎, 𝑥) = (1, 0) implies that 𝑥 = 𝓎.

Let R be an IF relation on X. R^–1 is called the inverse relation of R if R^–1(𝑥, 𝓎) = R(𝓎, 𝑥) for any 𝑥, 𝓎 ∈ X. Also, R^C is called the complement of R if R^C(𝑥, 𝓎) = (𝜈_{R(𝑥, 𝓎)}, 𝜇_{R(𝑥, 𝓎)}) for any 𝑥, 𝓎 ∈ X when R(𝑥, 𝓎) = (𝜇_{R(𝑥, 𝓎)}, 𝜈_{R(𝑥, 𝓎)}). It is obvious that R^–1 ≠ R^C.

Definition 2.3. ( [21]) Let R be an IF relation on X. The pair (X, R) is called an intuitionistic fuzzy approximation space. The intuitionistic fuzzy lower approximation of A ∈ IF(X) with respect to (X, R), denoted by , is defined as follows:

Similarly, the intuitionistic fuzzy upper approximation of A ∈ IF(X) with respect to (X, R), denoted by , is defined as follows:

The pair is called the intuitionistic fuzzy rough set of A with respect to (X, R).

Proposition 2.4. ( [17, 21]) Let (X, R) be an IF approximation space. Then for any A, B ∈ IF(X), {A_j ∣ j ∈ J} ⊆ IF(X) and (a, b) ∈ I ⊗ I,

Remark 2.5. Let (X, R) be an IF approximation space. Then

Let (X, R) be an IF approximation space. (X, R) is called a reflexive(resp., preordered) intuitionistic fuzzy approximation space, if R is a reflexive intuitionistic fuzzy relation (resp., an intuitionistic fuzzy preorder). If R is an intuitionistic fuzzy partial order, then (X, R) is called a partially ordered intuitionistic fuzzy approximation space. An intuitionistic fuzzy preorder R is called an intuitionistic fuzzy equality, if R is both an intuitionistic fuzzy equivalence and an intuitionistic fuzzy partial order.

Theorem 2.6. ( [17, 21]) Let (X, R) be an IF approximation space. Then

(1) R is reflexive

(2) R is transitive

Definition 3.1. ( [22]) Let (X, R) be an IF approximation space. Then A ∈ IF(X) is called an intuitionistic fuzzy upper set in (X, R) if

Dually, A is called an intuitionistic fuzzy lower set in (X, R) if A(𝓎) Λ R(𝑥, 𝓎) ≤ A(𝑥) for all 𝑥, 𝓎 ∈ X.

Let R be an IF preorder on X. For 𝑥, 𝓎 ∈ X, the real number R(𝑥, 𝓎) can be interpreted as the degree to which ‘𝑥 ≤ 𝓎 ’ holds true. The condition A(𝑥) Λ R(𝑥, 𝓎) ≤ A(𝓎) can be interpreted as the statement that if 𝑥 is in A and 𝑥 ≤ 𝓎, then 𝓎 is in A. Particularly, if R is an IF equivalence, then an IF set A is an upper set in (X, R) if and only if it is a lower set in (X, R).

The classical preorder 𝑥 ≤ 𝓎 can be naturally extended to R(𝑥, 𝓎) = (1, 0) in an IF preorder. Obviously, the notion of IF upper sets and IF lower sets agrees with that of upper sets and lower sets in classical preordered space.

Proposition 3.2. Let (X, R) be an IF approximation space and A ∈ IF(X). Then the following are equivalent:

Proof. (1) ⇒ (2). Suppose that . Since for each 𝑥 ∈ X,

we have

Thus A is a lower set in (X, R).

(2) ⇒ (3). This is obvious. (3) ⇒ (1). Suppose that A is an upper set in (X, R–1). Then for any 𝑥, 𝓎 ∈ X, A(𝑥) Λ R–1(𝑥, 𝓎) ≤ A(𝓎). So A(𝑥) Λ R(𝓎, 𝑥) ≤ A(𝓎). Thus

Hence .

Corollary 3.3. Let (X, R) be an IF approximation space and A ∈ IF(X). If R is reflexive, then the following are equivalent:

Proof. This holds by Theorem 2.6 and Proposition 3.2.

Proposition 3.4. Let (X, R) be an IF approximation space and A ∈ IF(X). Then the following are equivalent:

Proof. (1) ⇒ (2). Suppose that . Since for each 𝑥 ∈ X,

we have

Thus A^C is a lower set in (X, R).

(2) ⇒ (3). This is obvious. (3) ⇒ (1). Suppose that AC is an upper set in (X, R–1).

Then for any 𝑥, 𝓎 ∈ X, A^C(𝑥) Λ R^–1(𝑥, 𝓎) ≤ A^C(𝓎). So A^C(𝑥) Λ R(𝓎, 𝑥) ≤ A^C(𝓎). Thus

So

Hence .

Corollary 3.5. Let (X, R) be an IF approximation space and A ∈ IF(X). If R is reflexive, then the following are equivalent:

Proof. This holds by Theorem 2.6 and the above proposition.

For each z ∈ X, we define IF sets [z]^R : X → I ⊗ I by [z]^R(𝑥) = R(z, 𝑥), and [z]_R : X → I ⊗ I by [z]_R(𝑥) = R(𝑥, z).

Theorem 3.6. Let (X, R) be an IF approximation space. Then

(1) R is reflexive

(2) R is symmetric

(3) R is transitive

Proof. (1) and (2) are obvious. (3) By Proposition 3.2,

Also,

Proposition 3.7. Let (X, R) be an IF approximation space. Then

R is symmetric

Proof. By Remark 2.5, , because R is symmetric. Similarly we have that .

Theorem 3.8. Let R be an IF relation on X and let be an IF topology on X. If one of the following conditions is satisfied, then R is an IF preorder.

(1) is a closure operator of . (2) is an interior operator of .

Proof. Suppose that satisfies (1). By Remark 2.5, for each 𝑥 ∈ X. Since is a closure operator of , for each 𝑥 ∈ X,

Thus R is reflexive. For any 𝑥, 𝓎, z ∈ X, . Then by Remark 2.5 and Proposition 2.4,

Hence R is transitive. Therefore R is an IF preorder.

Similarly we can prove for the case of (2).

Definition 3.9. For each A ∈ IF(X), we define

Obviously, R_A = ∅ iff for some (a, b) ∈ I ⊗ I or A(𝑥) and A(𝓎) are non-comparable for all 𝑥, 𝓎 ∈ X.

Proposition 3.10. Let (X, R) be an IF approximation space. Let A be an IF set with constant hesitancy degree, i.e., A ∈ cIF(X) with R_A ≠ ∅. Then we have

Proof. (1) (⇒) Suppose that . Note that for each 𝑥 ∈ X,

Then A(𝓎) ∨ R^C(𝑥, 𝓎) ≥ A(𝑥) for any 𝑥, 𝓎 ∈ X. Since A(𝑥) > A(𝓎) for each (𝑥, 𝓎) ∈ R_A, we have

(⇐) Suppose that for each (𝑥, 𝓎) ∈ R_A, R^C(𝑥, 𝓎) ≥ A(𝑥) ∨ A(𝓎). Let z ∈ X.

(i) If A(z) > A(𝓎), then

(ii) If A(z) ≤ A(𝓎), then

A(𝓎) ∨ R^C(z, 𝓎) ≥ A(𝓎) ∨ (A(z) ∨ A(𝓎)) ≥ A(𝓎) ≥ A(z).

Hence for any z ∈ X. Thus .

Then A(𝑥) Λ R(𝓎, 𝑥) ≤ A(𝓎) for any 𝑥, 𝓎 ∈ X. Since A(𝑥) > A(𝓎) for each (𝑥, 𝓎) ∈ R_A, we have

(⇐) Suppose that for any (𝑥, 𝓎) ∈ R_A, R(𝓎, 𝑥) ≤ A(𝑥) Λ A(𝓎). Let z ∈ X.

(i) If A(𝑥) > A(z), then

(ii) If A(𝑥) ≤ A(z), then

A(𝑥) Λ R(z, 𝑥) ≤ A(𝑥) Λ (A(𝑥) Λ A(z)) ≤ A(𝑥) ≤ A(z).

Thus . Hence .

Corollary 3.11. Let (X, R) be a reflexive IF approximation space. Then for each A ∈ cIF(X) with R_A ≠ ∅,

Proof. By the above proposition and the reflexivity of R, it can be easily proved.

Let R₁ and R₂ be two IF relations on X. We denote R₁ ⊆ R₂ if R₁(𝑥, 𝓎) ≤ R₂(𝑥, 𝓎) for any 𝑥, 𝓎 ∈ X. And R₁ = R₂ if R₁ ⊆ R₂ and R₂ ⊆ R₁.

Proposition 3.12. Let (X, R₁) and (X, R₂) be two IF approximation spaces. Then for each A ∈ IF(X),

Proof. (1) For each 𝑥 ∈ X,

Thus we have . Dually,

Thus we have . Moreover, since R₁ ⊆ R₁ ∪ R₂ and R₂ ⊆ R₁ ∪ R₂, we have and Thus Hence we have . By Proposition 2.4,

Proposition 3.13. Let (X, R₁) and (X, R₂) be two reflexive IF approximation spaces. Then for each A ∈ IF(X),

Proof. (1) By Theorem 2.6, and . Thus we have

Similarly, we can prove that

(2) The proof is similar to (1).

Proposition 3.14. Let (X, R₁) and (X, R₂) be two IF approximation spaces. If R₁ is reflexive, R₂ is transitive and R₁ ⊆ R₂, then

Proof. By Theorem 2.6, For each 𝑥 ∈ X, by R₁ ⊆ R₂ and the transitivity of R₂, we have

Thus . So . By Proposition 2.4,

We obtained characteristic properties of intuitionistic fuzzy rough approximation operator and intuitionistic fuzzy relation by means of topology. Particularly, we proved that the upper approximation of a set is the set itself if and only if the set is a lower set whenever the intuitionistic fuzzy relation is reflexive. Also we had the result that if an intuitionistic fuzzy upper approximation operator is a closure operator or an intuitionistic fuzzy lower approximation operator is an interior operator in the intuitionistic fuzzy topology, then the order is an preorder.