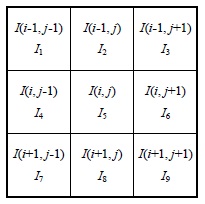Edge detection is an essential preprocessing for most image processing application, and there are several existing detection methods such as Sobel, Roberts, Laplacian, LoG(Laplacian of Gaussian) operators, etc. Those existing edge detection methods have not given satisfactory results since they do not offer enough pixel brightness change in low light level environment. Therefore, in this study new algorithms using brightness transfer function in the preprocessing and for edge detection applying standard deviation and average-weighted local masks are proposed. In addition, the performance of proposed algorithms was evaluated in comparison with the existing edge detection methods such as Sobel, Roberts, Prewitt, Laplacian, LoG operators.
에지 검출은 물체, 차선, 문자 검출 및 인식 과정 등에서 영상을 분할하기 위한 필수적인 전처리 과정이며, 군용 및 의료용 전자기기, 스마트 TV 및 스마트 폰, 자동 차량 인식기 등 여러 응용에 적용되고 있다[1].
일반적으로 널리 이용되고 있는 에지 검출 방법에는 Sobel, Roberts, Laplcian, LoG 방법 등이 있다. 이러한 방법들은 밝은 환경에서 에지 검출 특성이 대부분 우수하게 나타나며, 저조도 환경에서는 화소의 밝기 변화가 전반적으로 적으므로 에지 검출 특성이 미흡하다.
따라서 본 연구에서는 저조도 환경에서도 효과적으로 에지를 검출하기 위해, 전처리 과정에서 다항식을 사용한 휘도 변환 함수와 국부 마스크의 평균 및 표준편차에 따른 가중치를 적용하여 에지를 검출하는 알고리즘을 제안하였다. 그리고 제안한 알고리즘의 성능을 평가하기 위해, 저조도 환경에서 획득된 영상을 사용하여 기존의 Sobel, Roberts, Prewitt, Laplaician, LoG(Laplacian of Gaussian) 에지 검출 방법들과 제안한 알고리즘을 시뮬레이션하여 비교하였다.
본 논문의 구성은 다음과 같다. Ⅱ장에서 기존의 에지 검출 방법들에 대해 설명하고, Ⅲ장에서 휘도변환을 이용한 에지 검출 방법을 제안한다. Ⅳ장에서 기존의 방법과 제안한 방법을 시뮬레이션하여 결과를 비교한다. 마지막으로 Ⅴ장에서 본 논문의 결론을 내린다.
에지는 영상에서 물체와 물체 및 물체와 배경 사이의 화소 값이 급격하게 변화하는 영역에서 주로 나타난다. 이러한 특성을 갖는 에지를 검출하기 위한 기존의 에지 검출 방법에는 공간 영역에서 방향성 기울기 마스크들을 적용하는 방법과 2차 미분 연산자 Laplacian을 이용한 에지 검출 방법 등이 있다.
Sobel 에지 검출 방법은 공간 영역에서 수평 및 수직 방향의 기울기 마스크를 적용하는 방법이다. 이 방법으로 에지 검출 결과를 얻기 위해서는 먼저
여기서
Sobel 방법에 대한 최종 에지 출력은 식 (2)와 같이 수평 및 수직 기울기의 벡터합으로 구한다[2].
Roberts 에지 검출 방법은 공간 영역에서 45° 및 135° 대각선 방향의 기울기 마스크를 적용하는 방법이다. Roberts 방법에 사용되는 기울기 가중치 마스크를 영상에 적용하면 식 (3)과 같다[2].
Robert 방법에 대한 최종 에지 출력은 식 (2)와 같이 구한다.
Laplacian 에지 검출 방법은 공간 영역에서 2차 미분 연산자 Laplacian을 적용하여 에지를 구하는 방법이며, Laplacian 방법의 최종 에지 출력은 식 (4)와 같이 표현한다[3].
Laplacian 에지 검출 방법은 식 (4)와 같이 (
LoG 에지 검출 방법은 Gaussian 함수에 Laplacian을 적용하여 에지를 검출하는 방법이며, 이를 간단히 나타낸 것은 식 (5)와 같다[5].
여기서
일반적으로 저조도 환경에서 취득한 영상은 화소의 휘도 변화가 적으므로 에지 검출 특성이 미흡하게 된다. 이러한 문제점을 해결하기 위해 본 연구에서는 전처리 과정에서 화소를 적절한 크기로 변환하는 함수와 국부 마스크의 휘도 분포에 따라 적응 처리하여 에지를 검출하는 알고리즘을 제안하였다.
저조도 환경에서 에지 검출 특성이 미흡하므로 이를 보완하기 위해 저휘도, 중휘도, 고휘도의 화소를 적절한 크기로 변환하는 함수를 식 (6)과 같이 정의한다.
여기서
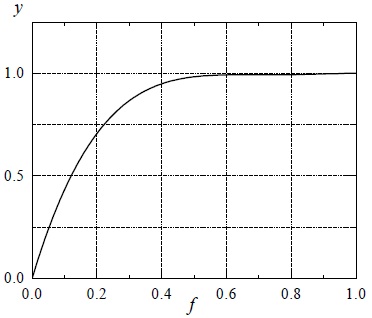
식 (6)의 다항식은 연산량이 많으므로 처리 시간이 길어지는 문제점이 있다. 따라서 휘도 변환을 적절히 하면서 연산량을 줄이기 위해 식 (6)의 휘도 변환 함수를 4차로 근사화하였으며, 그 변환 함수는 식 (7)과 같다.
식 (7)의 휘도 변환 함수의 형태는 그림 1과 같다.
영상에서 에지는 화소의 휘도가 급격하게 변하는 부분에 존재하며, 이러한 에지를 효과적으로 검출하기 위해 공간 영역에서 마스크의 평균 및 표준편차를 이용하여 가중치를 구한 후 에지를 검출한다. 제안한 알고리즘의 처리 과정은 다음과 같다.
먼저
일반적으로
여기서
국부 마스크의 화소 분포에 따라 적응 처리하기 위해, 분포 계수는 식 (8)과 (9)를 적용하여 식 (10)과 같이 구한다.
에지를 구하기 위한 임계값은 분포 계수를 마스크의 중심 화소에 가산하였으며, 식 (11)과 같다.
국부 마스크의 화소값들에 임계값을 적용하여 에지를 구하기 위한 가중치 마스크를 식 (12)와 같이 구한다.
최종 에지를 구하기 위한 추정 마스크는 원 영상에 가중치 마스크를 적용하여 식 (13)과 같이 구한다.
최종 에지 출력은 추정 마스크의 요소들 중 최대값과 최소값의 차에 의해 구하며, 식 (14)와 같이 나타낸다.
본 논문은 저조도 환경에서 기존의 에지 검출 방법들의 문제점을 보완하기 위해, 전처리 과정에서 조도를 개선하기 위한 휘도 변환 함수와 국부 마스크의 휘도 분포에 따라 적응 처리하여 에지를 구하는 알고리즘을 제안하였다. 제안한 알고리즘의 성능을 확인하기 위해 그림 3과 같이 저조도 환경에서 취득한 512×512 크기 8비트 그레이 레벨 영상을 사용하여 휘도 변환 함수를 적용하지 않은 경우의 에지 검출 성능과 휘도 변환 함수 적용한 경우의 에지 검출 성능을 시뮬레이션 하였다.
일반적으로 에지 검출의 정량적인 평가에는 PSNR(peak signal to noise ratio), PFOM(Pratt's figure of merit) 등이 있으며, 이러한 방법들은 평가 영상에 대한 ground truth 영상이 필요하다. 도형의 경우 이러한 ground truth 영상을 기준으로 평가하며, 대개의 경우는 영상이 복잡한 형태로 구성되고 이를 얻는 것이 불가하며 정량적인 평가가 어렵다[6-8]. 따라서 본 논문에서는 에지 검출 특성을 시각적 영상으로 나타내었다.
그림 4는 휘도 변환 함수 적용하지 않은 경우의 결과 이며, (a)는 Sobel, (b)는 Roberts, (c)는 Prewitt, (d)는 Laplacian, (e)는 LoG 에지 검출 방법으로 처리한 영상이고, (f)는 제안한 휘도 변환 함수 에지 검출 알고리즘으로 처리한 영상이다.
그리고 그림 5는 휘도 변환 함수 적용 한 경우의 결과이며, 휘도 변환 함수에 적용된 계수는 각각
그 결과, 그림 4에서 (a)는 비교적 양호한 에지 검출 결과를 나타내었고, (b)는 에지 검출 특성이 전반적으로 미흡하였다. (c)는 일부 영역에서 에지 검출 특성이 미흡하였고, (d)는 에지 검출 특성이 가장 미흡하였다. (e)는 특정 영역에서 에지 검출 특성이 양호하였으며, 일부 영역에서는 검출 오류를 나타내었다. 그리고 (f) 는 기존의 방법들에 비해 우수한 에지 검출 특성을 나타내었다.
그리고 그림 5에서 (a)는 고휘도 및 중휘도 영역에서 우수한 검출 특성을 나타내었으며, 저휘도 일부 영역에서는 에지를 검출 오류를 나타내었다. (b)는 일부 영역의 에지를 검출하였고, 많은 검출 오류를 나타내었다. (c)는 고휘도 및 중휘도 영역에서 우수한 에지 검출 특성을 나타내었으며, 일부 영역의 에지 검출 특성은 다소 미흡하였다. (d)는 전반적인 에지 검출 특성이 미흡하였다. (e)는 고휘도 영역 및 중휘도 영역에서 에지 검출 특성이 양호하였으며, 일부 영역에서는 에지를 누락하여 검출 결과가 다소 미흡하였다. 그리고 (f) 는 저휘도, 중휘도 및 고휘도 영역에서 우수한 에지 검출 특성을 나타내었다.
본 논문은 저조도 환경에서 기존의 에지 검출 방법들의 검출 특성을 개선하기 위해, 전처리 과정에서 휘도 변환 함수와 국부 마스크의 휘도 분포에 따라 적응 적으로 에지를 검출하는 알고리즘을 제안하였다.
제안한 알고리즘의 성능을 평가하기 위해 기존의 방법들과 제안한 알고리즘을 시뮬레이션하여 시각적 영상으로 비교하였으며, 그 결과, 휘도 변환 함수를 적용하지 않은 경우, Sobel 에지 검출 방법은 저휘도 영역에서 에지 검출 특성이 미흡하였으며, Roberts 에지 검출 방법은 중휘도 및 저휘도 영역에서 에지 검출 특성이 미흡하였다. Prewitt 에지 검출 방법은 Sobel 에지 검출 방법과 유사한 검출 특성을 나타내었으며, Laplacian 에지 검출 방법은 전반적으로 검출 특성이 미흡하였다.
그리고 LoG 에지 검출 방법은 특정 영역에서 에지 검출 특성이 양호하였으며, 일부 영역에서는 에지 검출 오류를 나타내었다. 그리고 제안한 휘도 변환 함수 에지 검출 알고리즘은 기존의 방법들에 비해 전반적으로 우수한 에지 검출 특성을 나타내었다. 그리고 휘도 변환 함수를 적용한 경우, 기존의 에지 검출 방법들에 비해 제안한 휘도 변환 함수 에지 검출 알고리즘은 고휘도, 중휘도 및 저휘도 영역에서 우수한 에지 검출 특성을 나타내었다.
따라서, 제안한 알고리즘은 저조도 환경의 물체 검출, 차선 인식, 문자 인식 등의 여러 응용 분야에서 유용하게 활용되리라 사료된다.
