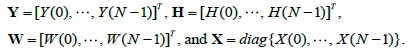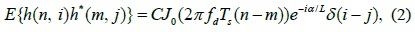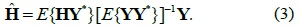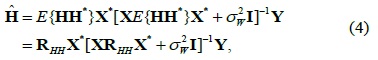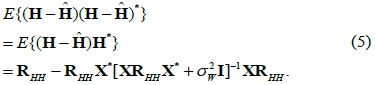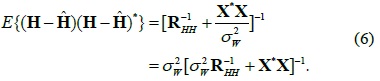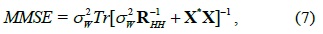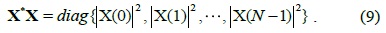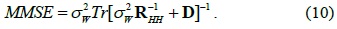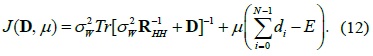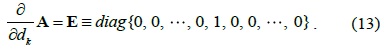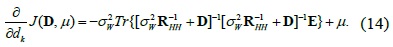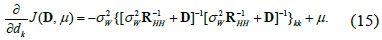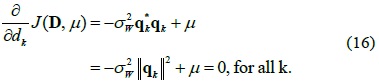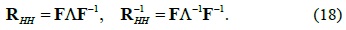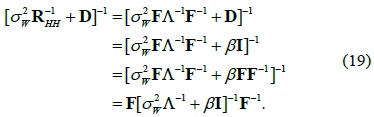Orthogonal frequency division multiplexing (OFDM) is a widely used technique for high-speed data transmission in a frequency-selective fading environment. To achieve a high data rate as well as good performance, coherent detection is commonly used in most of the existing OFDM systems [1]. Coherent detection relies on the knowledge of the channel state information (CSI). One simple approach to obtain CSI is to send sounding symbols from the transmitter.

Many studies have been conducted on sounding signal design and channel estimation in pilot symbol-assisted OFDM (PSA-OFDM) systems. The locations of these sounding symbols along with the data stream, i.e., the sounding signal pattern, were examined in [2] and [3]. Other techniques for optimal sounding signal design that use the least-squares (LS) or the minimum mean square error (MMSE) method for OFDM channel estimation can be found in [4] and [5]. In particular, in [6], necessary and sufficient conditions were derived for optimal training sequences for the LS method, and a lower bound on the variance of the channel estimation was derived. In [7], an optimal design was considered by minimizing the channel mean square error (MSE). In [8], the symbol error rate was employed as a criterion for the optimization of the sounding signal design. In [9], pilot signal optimization for channel estimation was considered to be a minimization problem and was solved with iterative algorithms. Several approaches have been proposed for the sounding signal of MIMO systems, but not all these approaches have been mathematically verified with prior statistical information about the channel. In [10], an MSE performance close to that obtained by optimal orthogonal sequences was achieved at a considerably low implementation complexity. There are several methods for MIMO-OFDM systems with the general case of spatial correlations reported in [11] and [12].

In this paper, we derive the optimal sounding signal characteristics for MMSE channel estimation assuming that second-order channel statistics are known in the SISOOFDM case. Furthermore, we show that a maximal-length shift register sequence (M-sequence) is appropriate for the optimal training sequence.

The rest of this paper is organized as follows: Section II presents the mathematical model of channel estimation for SISO-OFDM systems and implements the optimal training sequence design on the basis of the MMSE criterion. Section III verifies an optimal sounding signal design to optimize the training sequences for a general MMSE criterion. Simulation results are provided in Section IV, and conclusions are drawn in Section V.

We have formulated the following SISO-OFDM MMSE system model for channel sounding:

where

Note that Y(k) denotes the fast Fourier transform (FFT) of the received sounding signal, H(k) represents the channel frequency response, W(k) indicates the noise, and X(k) refers to the amplitude of the sounding signal in the k-th subcarrier out of N subcarriers.

Our model of the second-order statistics of the channel can be described as in [13]:

where E(•) reprents the expectation of a random variable, h(p, q) denotes the channel impulse response from the p-th time slot to the q-th channel tap, (•)^* denotes a complex conjugate transpose, C indicates a constant value of the amplitude of the channel element, J₀ (•) refers to the Bessel functions of the first kind, f_d indicates the Doppler frequency, T_s represents the symbol duration, α denotes the decay factor, L refers to the multipath delay spread in samples, and δ (•) denotes the Dirac delta function.

The standard MMSE estimate of H, based on the observation of Y, is written as follows:

Using (1), we can express as follows:

where denotes the variance of the noise, I represents the identity matrix, and R_HH = E {HH^*} indicates the covariance matrix of the channel matrix, H.

The covariance matrix can be expressed as follows:

By applying the well-known matrix identity, (A+BCD)^-1 = A^-1 - A^-1B (C^-1+DA^-1B)^-1DA^-1, we can rewrite (5) as follows:

Therefore, the MMSE of H can be derived as follows:

where Tr denotes the trace of an square matrix.

We consider finding a sounding signal that minimizes the MMSE, subject to the following energy constraint:

To solve this problem, we need to find the diagonal matrix X that minimizes (7) subject to the above constraint. Recall that the diagonal elements of X are the sounding signal amplitudes in all subcarriers as defined above.

As in (9), the MMSE depends not on the phase angles of the sounding signal in all subcarriers but on their magnitudes. Let us, therefore, assume that d_k = |X(k)|² and D = X^*X = diag {d₀,d₁,...,d_N-1}. Then, (7) can be expressed as follows:

Thus, we have the ultimate goal of obtaining the nonnegative diagonal elements d_k by minimizing (10) subject to the following constraint:

We can mathematize the objective function in (10) by using the Lagrange multiplier method with the constraint defined in (11). By letting μ be the Lagrange multiplier, we can formularize the Lagrange equation J (D, μ) as follows:

Thus, we set ∂J(D,μ)/∂d_k = 0. Using the property that for any matrix A depending on a parameter x, ∂A^-1/∂x = -A^-1 (∂A/∂x)A^-1, which involves AA^-1 = I, we can solve the partial differentiate ∂J(D,μ)/∂d_k by substituting and d_k for A and x, respectively, as follows:

Note that 1 in (13) is the k-th diagonal element. Thus, by applying the property Tr(AB) = Tr(BA) to (12), we acquire the following:

By considering Tr {ME} = M_kk , which is the k-th diagonal element of any diagonal matrix M, we can rewrite (14) as follows:

By defining q_k as the k-th column of in (15) and using the fact that is Hermitian, we conclude that

We can show that the optimum D results in all q_k having an equal norm. Further, we verify that the solution that satisfies these conditions is that all d_k should be equal; i.e., all sounding signal amplitudes in all subcarriers should have an equal magnitude, or equivalently, D should be a multiple of the identity matrix. First, the channel matrix can be expressed as follows:

where h denotes the impulse response matrix of the channel and F represents the FFT matrix. Therefore, it can be shown readily that R_HH represents a circulant matrix assuming that the impulse response taps are uncorrelated. As is well known, R_HH can be expressed as follows:

By assuming that D is a multiple of the identity matrix, D = βI, we can rewrite (18) as follows:

Since is a diagonal matrix, the matrix of (19) is a circulant matrix. Because its columns have an equal norm and the matrix D satisfies the equations of optimality, the optimum sounding signal has sounding signal amplitudes with equal magnitudes in all subcarriers across the frequency band.

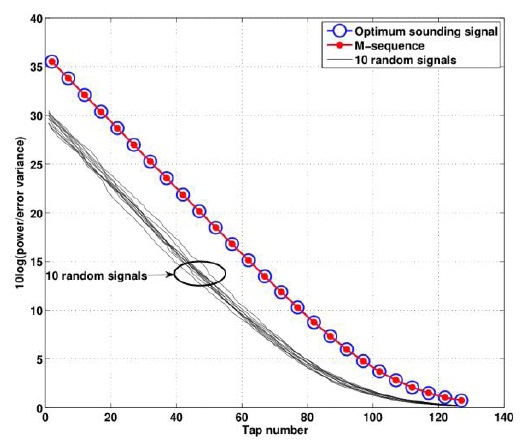
In Fig. 1, the curve marked with blue circles corresponds to the performance of the optimum sounding signal, and the other curves are for 10 different sounding signals whose amplitudes in all subcarriers are complex Gaussian random variables, independent of the frequency. The simulation parameters are as follows: guard interval of length 128, T_g = N = 128, average signal-to-noise power ratio (SNR) = 20 dB, decay parameter α = 10, the number of sounding symbols M_s = 1, and the Doppler bandwidth is f_dT_s = 0. The FFT of the autocorrelation function of the sounding signal is identical to the squared magnitude of the transform of the signal itself. Since the optimum autocorrelation function is an impulse in the time domain, the optimum sounding signal outperforms the random sounding signals.

In addition, Fig. 1 presents a comparison of the optimum sounding signal and an M-sequence. Note that the performance of the M-sequence is indistinguishable from that of the optimum sounding signal, since the autocorrelation of the M-sequence corresponds approximately to an impulse in the time domain.

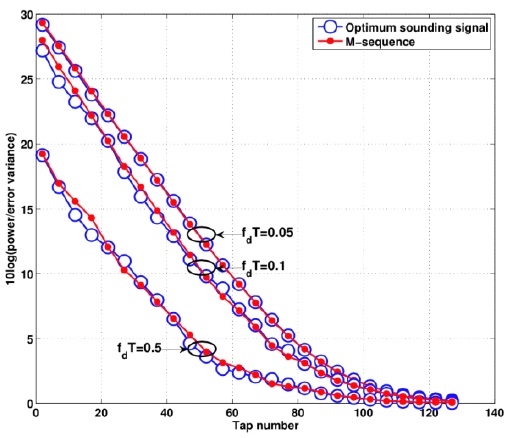
Fig. 2 presents a comparison of the BER performance in the cases of the optimum sounding signal and the M-sequence for several different Doppler effects. The simulation parameters are identical to those considered in Fig. 1, except for the Doppler effect . f_dT_s. We can show that the M-sequence has a comparable performance to the optimum sounding signal in all cases, f_dT_s = 0.05, 0.1, and 0.5.

In this paper, we derived the optimal sounding signal characteristics for MMSE channel estimation assuming that the second-order channel statistics are known in the SISO-OFDM case. We found that the optimum sounding signal has an equal magnitude in all subcarriers across the frequency band. Through simulations, we found that the optimal sounding signal outperforms random sounding signals. In addition, we showed that the M-sequence is appropriate as an optimal training sequence.