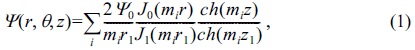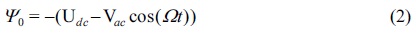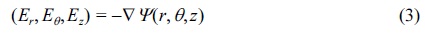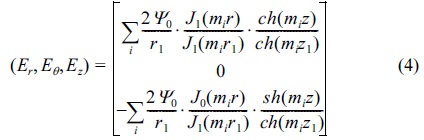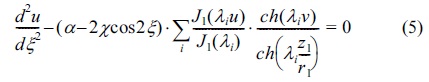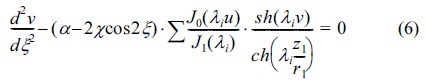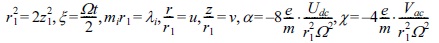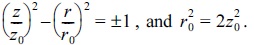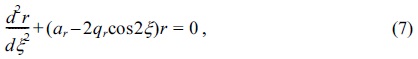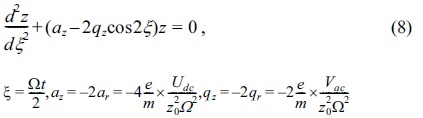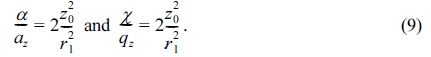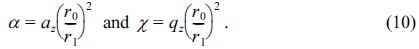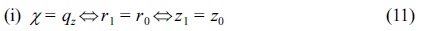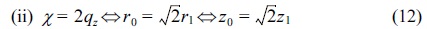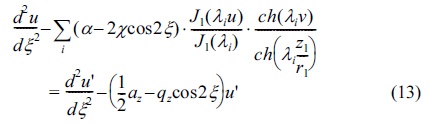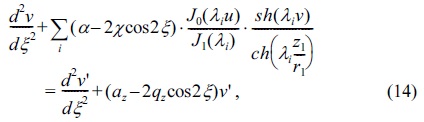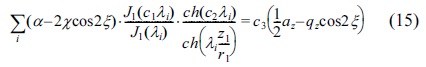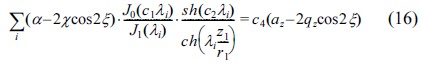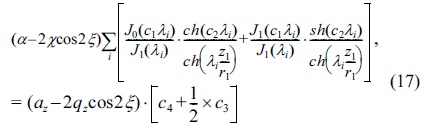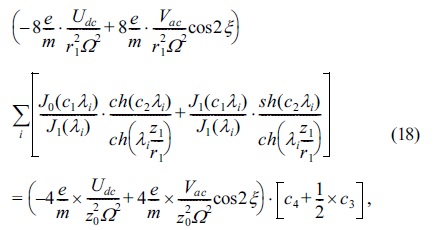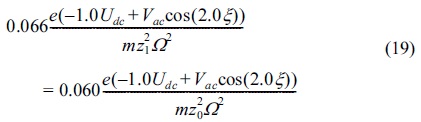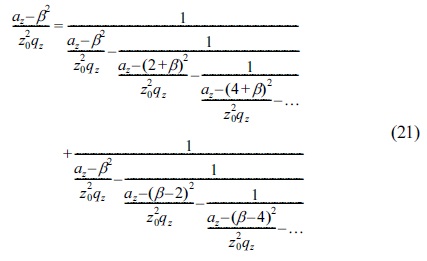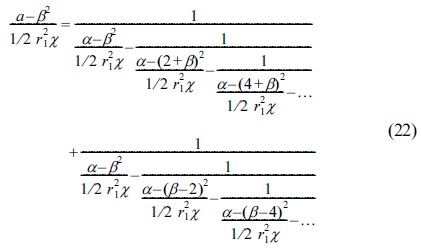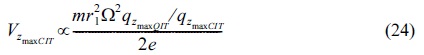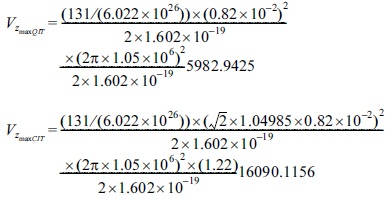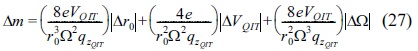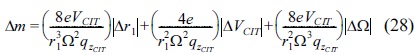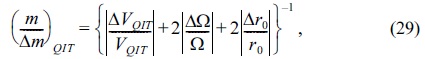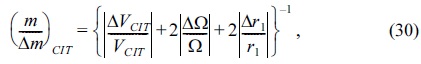Ion trap mass spectrometry has been developed through several stages to its present situation of relatively high performance and increasing popularity. Quadrupole ion trap (QIT), invented by Paul and Steinwedel,1 has been widely applied to mass spectrometry,2-11 ion cooling and spectroscopy,12 frequency standards, quantum computing,13 and so on. However, various geometries has been proposed and used for QIT.14

An ion trap mass spectrometer may incorporate a Penning trap,15 Paul trap16 or the Kingdon trap.17 The Orbitrap, introduced in 2005, is based on the Kingdon trap.18 Also, the cylindrical ion trap CIT has received much attention in a number of research groups because of several merits. The CIT is easier to fabricate than the Paul ion trap which has hyperbolic surfaces. In addition, the relatively simple and small sized CIT make it an ideal candidate for miniaturization. Experiments using a single miniature CIT showed acceptable resolution and sensitivity, and limited by the ion trapping capacity of the miniature device.19-21

With these interests, many groups such as Purdue University and Oak Ridge National Laboratory have researched on the applications of the CIT to miniaturize mass spectrometer.22,23

In CIT, the hyperbolic ring electrode,24 as in Paul ion trap, is replaced by a simple cylinder and the two hyperbolic end-cap electrodes are replaced by two planar end-plate electrodes.25 The potential difference applied to the electrodes24-26 is:

with

Where, U_dc is a direct potential, V_ac is the zero to peak amplitude of the RF voltage, Ω is RF angular frequency, and z₁ expresses the distance from the center of the CIT to the end cap and r₁ the distance from the center of the CIT to the nearest ring surface. The electric field in a cylindrical coordinate (r, z,θ) inside the CIT can be written as follows:

here, ▽ is gradient. From Eq.(3) (grad), the following is retrieved:

he equation of the motions10,21,24,25 of the ion of mass m and e can be written as

and the following

Where J₀ and J₁ are the Bessel functions of the first kind of order 0 and order 1, respectively, whereas ch is the hyperbolic cosine function, m_ir is the roots of equation J₀ (m_ir) = 0. To obtain λ_i’s the Maple software was employed to find J₀ (λ_i) = 0 roots. Eqs.(5) and (6) are coupled in u and v (respective r and z), and thus, can only be treated as a rough approximation.21,25 Therefore, studies on CIT equations are more difficult and complex compared to QIT equations. As stated earlier, the optimum radius size between CIT and QIT helps us to study QIT instead of CIT.27

A hyperbolic geometry for the Paul ion trap was assumed;

Here, z₀ is the distance from the center of the QIT to the end cap and r₀ is the distance from the center of the QIT to the nearest ring surface. In each of the perpendicular directions r and z, the ion motions of the ion of mass m and charge e5,24,28,29 may be treated independently with the following substitutions:

If the ions the same species are taken into consideration and the same potential amplitude and frequency, the following relations has been obtained:

From Eq.(9) and one can obtain

In some papers,21,24 stability parameters have been used to determine the optimum radius size for cylindrical ion trap compared to the radius size for the quadrupole ion trap, as following:

Eqs.(11) and (12) are from Refs,21,24 respectively. In this study, Eqs.(5), (6) and Eqs.(7), (8) were used for the same propose to find optimum radius size for cylindrical ion trap compared to the radius size for quadrupole ion trap, as:

with u' = r/r₀ and v' = z/z₀. Where α and χ are the trapping parameters, which λ_i is the root of equation J₀ (m_ir₁)=0. Eqs.(13) and (14) are true when (α,χ) and (a_z,q_z) vqlues belong to stability regions. In this case, u = u(0) = c₁, v = v(0) = v₂, u' = u'(0) = c₃, and v = v(0) = v₄, were assumed. Here, u(0), v(0), u'(0), v'(0) are the initial values for u,v,u' and v', respectively. Now, from Eqs.(13) and (14) with d²u/dξ² = d²c₁/dξ² = 0, d²v/dξ² = d²c₂/dξ² = 0, d²u'/dξ² = d²c₃/dξ² = 0 and d²v'/dξ² = d²c₄/dξ² = 0, the following can be obtained:

In adding Eqs.(15)and (16), we have:

After substituting α,χ,α_z and q_z we have,

with Eq.(18) gives the optimum value of z₁ and z₀ for CIT and QIT with conditions c₁ = c₃ and c₂ = c₄. After substituting λ_i',s,c₁ = c₃ = 0.01 and c₂ = c₄ = 0.01 ; in Eq.(18) and by simplification, we have:

Therefore, using the Maple software we will have,

In Eq.(20), z₁ = 1.01978z₀ is the optimum radius size between the quadrupole and the cylindrical ion traps. For any initial conditions we can obtain same answer with Eq.(20) almost. This optimal radius size (z₁ = 1.04978z₀) is almost comparable with the optimal radius size in Eq.(11)(z₁ = z₀) when χ = q_z21,24 For the various u; v; r; z when (α, χ) and (a_z,q_z) belongs to the stability regions, we found almost the comparable optimum values equivalent to Eq. (20) was found. For example with c₁ = c₃ = 0.005, c₂ = c₄ = 0.01 and c₁ = c₃ = 0.05, c₂ = c₄ = 0.01, we have z₁ = 1.4976z₀. and z₁ = 1.05024z₀.

There are two stability parameters which control the ion motion for each dimension z (z = u or z = v) and (z = z or z = r), and a_z, q_z in the case of cylindrical and quadrupole ion traps,24 respectively. In the plane (a_z, q_z) and for the z axis, the ion stable and unstable motions are determined by comparing the amplitude of the movement to one for various values of a_z, q_z.26,30 To compute the accurate elements of the motion equations for the stability diagrams, we have used the fifth order Runge-Kutta numerical method with a 0.001 steps increment for Matlab software and scanning method.

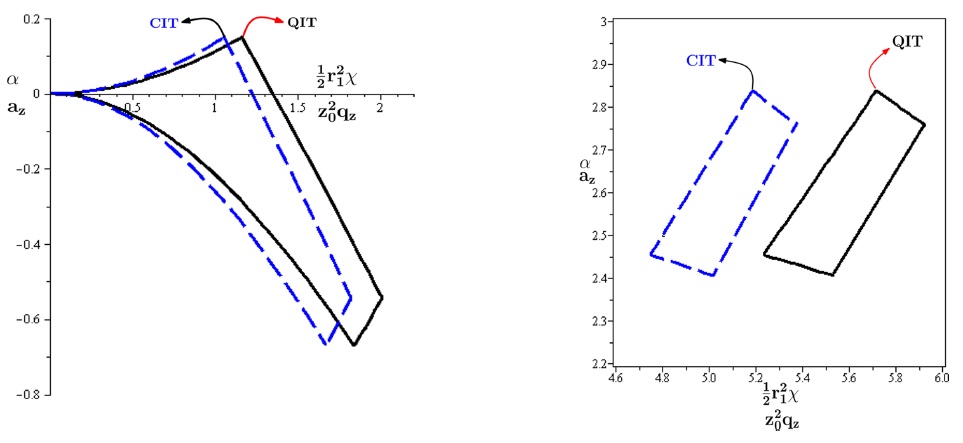
Figure 1 (a) and (b) shows the calculated first and second stability regions for the quadrupole ion trap and cylindrical ion trap,31) black line (solid line): QIT and blue line (dash line): CIT with optimum radius size z₁ = 1.04978z₀, (a): first stability region and (b): second stability region. Figure 1 shows that the apex of the stability parameters a_z stayed the same and the apex of the stability parameters q_z decrease for CIT to compare with QIT. Area of first stability regions for QIT and CIT are almost same, as 0.4136 and 0.4087, respectively. Figure 1 reveals almost a comparable stability diagram two methods.

Figure 2 shows evolution of different values of the phase ion trajectory for ξ₀ with red line : QIT with z₀ = 0.82 cm and blue line: CIT with the optimum radius size

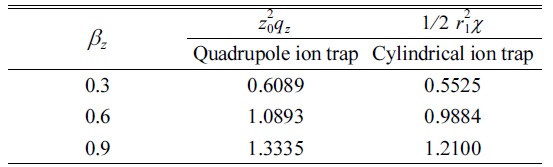
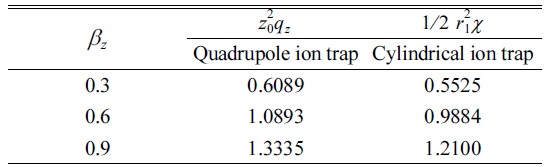
The results illustrated in Figure 2 show that for the same equivalent operating point in two stability diagrams (having the same β_z), the associated modulated secular ion frequencies behavior are almost same for the quadrupole and cylindrical ion traps with the optimum radius size z₁ = 1.04985z₀. Table 1 presents the values of for the quadrupole and cylindrical ion traps, when a_z = 0 and α = 0 with the optimum radius size z₁ = 1.04985z₀, respectively for β_z = 0.3.;0.6;0.9. For the computations presented in Table 1, the following formulas were used:

and

for QIT and CIT, respectively. Hence, it is important to know that β_z point are the equivalent points; two operating points located in their corresponding stability diagram have the same β_z.31 For the same 0< β_z <1 we have, Here, 1.35 and 1.23 are maximum values of stability diagrams for QIT and CIT when a_z = 0 and α = 0 respectively. Therefore, for β_z = 0 we have and for β_z = 1 we have for QIT and CIT, respectively. To compute Table 1, Maple software have been used.

he resolution of a quadrupole ion trap9 and cylindrical ion trap mass spectrometry in general with optimum radius size z₁ = 1.04985z₀, is a function of the mechanical accuracy of the hyperboloid of the QIT Δr₀, and the cylindrical of the CIT Δr₁, and the stability performances of the electronics device such as, veriations in voltage amplitude ΔV, the rf frequency ΔΩ,9 which tell us, how accurate is the form of the voltage signal.

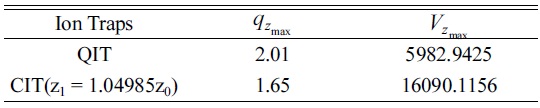
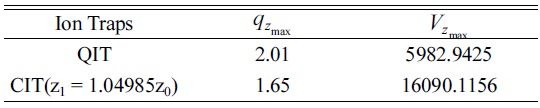
Table 2 shows the values of q_zmax and V_zmax or the quadrupole ion trap and cylindrical ion trap with optimum radius size size z₁ = 1.04985z₀ in the first stability region

when a_z = 0, respectively. The value of V_zmax has been obtained for ¹³¹Xe with Ω = 2Π × 1.05 × 10⁶ rad/s, U = 0 V and z₀ = 0.82 cm in the first stability region when a_z = 0.

To obtain the values of Table 2 we suppose V_zmax as function of for QIT and CIT with z₁ = 1.04985z₀, respectively as follows,

Now, we use Eqs.(23) and (24) to calculate V_zmaxQIT and V_zmaxCIT for ¹³¹Xe with Ω = 2Π×1.05×10⁶ rad/s, z₀ = 0.82 cm and z₁ = 1.04985z₀ as follows,

To derive a useful theoretical formula for the fractional resolution, one has to recall the stability parameters of the impulse excitation for the QIT and CIT with z₁ = 1.04985z₀, respectively as follows,

By taking the partial derivatives with respect to the variables of the stability parameters q_zQIT for Eq.(25) and q_zCIT for Eq.(26), then the expression of the resolution Δm of the QIT and CIT, respectively are as follows,

Now to find the fractional resolution we have,

Here Eqs.(29) and (30) are the fractional resolutions for QIT and CIT with optimum radius size z₁ = 1.04985z₀, respectively.

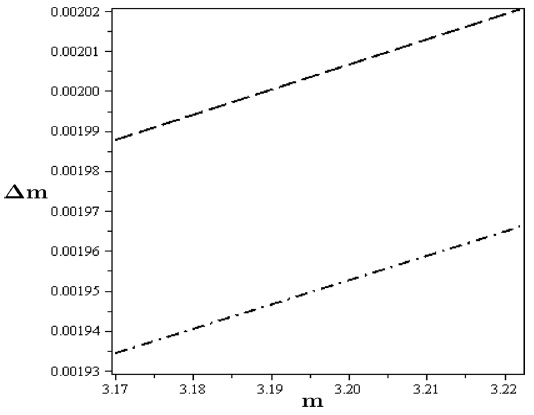
For the fractional mass resolution we have used the following uncertainties for the voltage, rf frequency and the geometry; ∆V / V = 10^-15, ∆Ω / Ω = 10^-7, ∆r₀ / r₀ = 3×10^-4. The fractional resolutions obtained are m/∆m = 1638.806949;1638.398047 for QIT and CIT with optimum radius size z₁ = 1.04985z₀, respectively. When optimum radius size z₁ = 1.04978z₀ is applied, the rf only limited voltage is increased by the factor of approximately 2.6893, therefore, we have taken the voltage uncertainties as ∆V_CIT / V_CIT = 2.6893 × 10^-5. From Eqs.(29) and (30) we have (m/∆m)_QIT = 1638.8069 and (m/∆m)_CIT = 1598.6598 for QIT and CIT with optimum radius size z₁ = 1.04985z₀, recpectively. When these fractional resolutions are considered for the ¹³¹Xe isotope mass m = 3.18, then, we have ∆m = 0.001940436 and 0.001994156 for QIT and CIT with optimum radius size z₁ = 1.04978z₀, respectively. This means that, as the value of m/∆m is decreased, the resolving power is increased due to increment in ∆m. Experimentally, this means that the width of the mass signal spectra is better separated.

In this study, the behavior of the quadrupole and cylindrical ion traps with the optimum radius has been considered. Also, it is shown that for the same equivalent operating point in two stability diagrams (i.e. having the same β_z = 0.3), the associated modulated secular ion frequencies behavior are almost the same with a suitable optimum radius size z₁ = 1.04978z₀ with This optimal radius size (z₁ = 1.04978z₀) is almost comparable with the optimal radius size in Eq.(11) (z₁ = z₀) when x = q_z22,25

Table 1 also indicate that for the same equivalent operating point, almost a comparison physical size between two ion traps are shown; z₁ = 1.04978z₀ = 0.86 cm and z₀ = 0.82 cm. The CIT has a smaller trapping parameter compared to QIT; for example for β_z = 0.3 we have a difference of 0.0564 higher for the QIT.

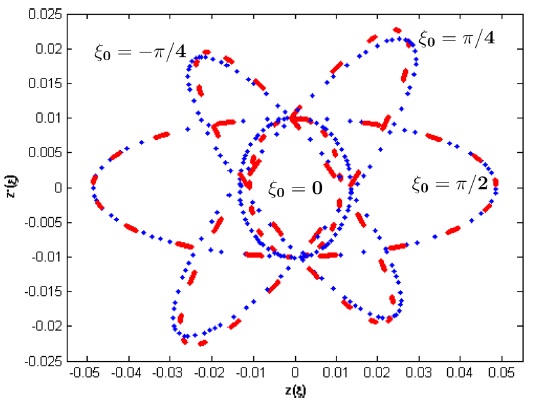
This difference in trapping parameters indicates that for the same rf and ion mass values, we need more confining voltage for CIT than QIT (see Table 2). So, higher fractional resolution can be obtained; higher separation confining voltages, especially for light isotopes9,31 (see Figure 3).