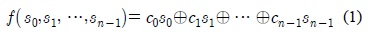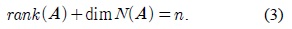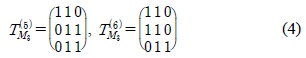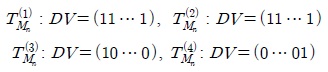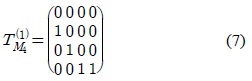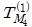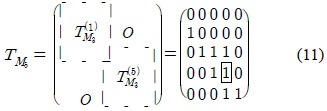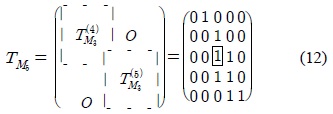LFSR 기반의 패턴분류기의 생성 및 분석

doi:10.6109/jkiice.2015.19.7.1577

OA학술지
Journal of the Korea Institute of Information and Communication Engineering

LFSR 기반의 패턴분류기의 생성 및 분석 Generation and Analysis of Pattern Classifier based on LFSRs

DOI : 10.6109/jkiice.2015.19.7.1577
Publish: Journal of the Korea Institute of Information and Communication Engineering Volume 19, Issue7, p1577~1584, July 2015

ABSTRACT

LFSR 기반의 패턴분류기의 생성 및 분석

In this paper, we propose a method for generating pattern classifier based on LFSR. The proposed pattern classifier bosed on LFSR is easy to see non-reachable state, and we can obtain dependency vector by using the 0-basic path. Also, we propose a method for generating pattern classifiers based on LFSR which correspond to given dependency vector.

KEYWORD

LFSR , 패턴분류기 , 의존벡터 , 끌개 , 0-기본경로

본문

Collapse all

Ⅰ. 서 론

패턴인식의 처리 과정은 패턴의 특징을 파악하여 패턴이 속한 부류로 분류하는 과정으로 구성되며, 패턴인식의 대부분인 분류 작업은 패턴분류기에 의하여 이루어진다. 패턴분류기는 데이터로부터 패턴들의 중요한 특징이나 속성을 추출하여 패턴을 특정한 클래스에 할당한다[1-3]. 패턴분류기의 설계는 작은 저장 공간, 큰 데이터 처리량, 낮은 가격대로 구현하는 것을 고려하여야 한다.

메모리 량을 최소화 할 수 있는 방법으로 Maji 등은 클래스의 수가 2개인 패턴을 효과적으로 분류할 수 있는 MACA(Multiple Attractor Cellular Automata)를 합성하여 패턴분류기를 설계하였다[3]. Maji 등은 의존벡터(Dependency Vector, 이하 DV)를 이용하여 시간복잡도를 O(n³)에서 O(n)으로 줄였다. 그러나 DV를 구하기 위하여 MACA에 대응하는 0-트리에 속하는 모든 원소를 구하여 그것을 계수로 하는 동차연립방정식의 해를 구하야 하므로 초기 설정시간이 오래 걸린다.

본 논문에서는 초기 설정시간을 효과적으로 줄이기 위해 LFSR(Linear feedback shift register) 기반의 패턴 분류기를 생성한다. 생성한 LFSR 기반의 패턴분류기 의 상태전이행렬에 대한 특성을 분석하여 주어진 의 상태전이그래프에서 0-트리의 한 도달불가능한 상태를 구하는 방법을 제안한다. 따라서 에 대응하는 DV를 구하는 시간을 효과적으로 줄일 수 있다. 또한 주어진 n-셀 DV에 대응하는 LFSR 기반의 패턴분류기 의 상태전이행렬 T_{M_n}에 대하여, DV_i 에 대응하는 T_{M_i}를 합성하여 생성할 수 있다.

Ⅱ. 배경 지식

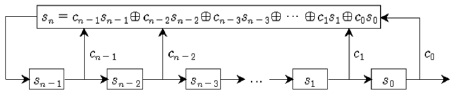
의사난수열 생성, 암호화 시스템 구현 등에 이용되는 LFSR은 시프트 레지스터의 일종으로, 레지스터에 입력되는 값이 이전 상태 값들의 선형 함수로 계산되고 유한체 위에서 정의된 선형점화식 수열을 효율적으로 발생시킬 수 있다. 이러한 수열의 특성은 점화식에 의해 유도되는 특성다항식에 의하여 결정된다[4,5]. n개의 셀과 선형 피드백 함수(Linear feedback function) f(s₀,s₁,⋯,s_n_-1) 로 구성되는 n차 LFSR은 식(1)과 같다[6].

여기서 s₀,s₁,⋯,s_n_-1는 레지스터에 입력되는 초깃값이고 c₀,c₁,⋯,c_n_-1 ∈ GF(2) 이다.

그림1은 n차 LFSR의 구조이다. 식(1)에 대한 다항식 c_T(x) = xⁿ + c_n_-1 xⁿ^-1 + ⋯ + c₀를 LFSR의 특성다항식 (Characteristic polynomial)이라 한다[7].

[그림 1.] LFSR의 구조

다음은 본 논문에서 사용되는 용어에 대한 정의이다.

<정의2.1[8-10]>

다항식 f(x) = xⁿ + c_n_-1 xⁿ^-1 + c_n_-2 xⁿ^-2 + ⋯ + c₁x + c₀ (c_i ∈ GF(2), 0 ≤ i ≤ n-1)에 대해 아래와 같은 n × n 행렬 T를 f (x)의 동반행렬(Companion matrix)이라고 하고[7], 다음 식(2)와 같이 4가지 형태로 나타낼 수 있다.

n차 LFSR은 X_t = TX_t_-1로 표현할 수 있다. 여기서, X_i는 시간 i 에서의 n × 1 상태벡터이고 T는 동반행렬로 표현할 수 있다. 동반행렬 T에 대하여 c_T(x) = m_T(x)이 성립한다[7]. 단 m_T(x)는 T의 최소 다항식(Minimal polynomial)이다.

<정리 2.2[11]> 임의의 m × n 행렬 A 에 대하여 다음이 성립한다.

앞으로 c_T(x) = m_T(x) = xⁿ^-1(x+1)인 2개의 끌개를 갖는 패턴분류기를 로 나타내기로 한다.

<정의 2.3[3]> 의존벡터(Dependency Vector, 이하 DV)는 n비트 패턴들로 구성된 벡터공간의 부분공간 의 모든 원소에 대하여 성립하는 변수들 간의 선형 종속 관계이다. DV와 0-트리의 성분의 내적은 0이다.

DV = (101)인 패턴분류기 의 상태전이행렬 T_M_₃은 다음 식(4)과 같이 두 가지 경우가 있다.

Ⅲ LFSR 기반의 패턴분류기

이 절에서는 LFSR을 이용한 패턴분류기를 생성하고 0-기본경로를 이용하여 DV를 구할 수 있는 방법을 제안한다. n-셀 패턴분류기 의 상태전이행렬 T_{M_n}에 대하여 C_{T_{M_n}}(x) = m_{T_{M_n}}(x) = xⁿ^-1(x+1)이 성립한다. 이때 끌개의 개수는 2개이고, 0-트리의 상태의 개수는 2ⁿ^-1개다. 그리고 rank(T_{M_n}) = n-1이다. c_{T_{M_n}}(x) = m_{T_{M_n}}(x) = xⁿ^-1(x+1)인 n-셀 패턴분류기 의 상태전이행렬 T_{M_n}에 대하여 대각성분의 1의 개수는 홀수이다.

<정리 3.1[12]> 상태전이행렬이 T_{M_n}인 n-셀 패턴분류기 의 상태전이그래프에서, x가 0-트리의 한 도달불가능상태일 때 DV는 0-기본경로 의 성분을 각 행으로 하는 행렬 (B₀)의 영공간 N(B₀)의 기저벡터이고 유일하다.

위 정리로부터 0-트리의 도달불가능상태를 알면 0-기본경로를 알 수 있으므로 DV를 구하기가 쉽다는 것을 알 수 있다.

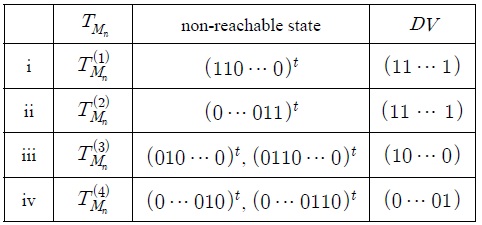
LFSR 기반의 n-셀 패턴분류기 의 상태전이행렬 T_{M_n}은 다음 식(5)과 같이 4가지 형태로 나타낼 수 있다.

<정리 3.2> 길이가 n인 LFSR 기반의 패턴분류기 의 상태전이행렬 T_{M_n}에 대하여, e_i 를 크기가 n이고 i번째 성분이 1인 단위벡터 일 때, 의 상태전이그래프에서 0-트리의 한 도달불가능한 상태 x는 다음과 같다.

증명> 의 상태전이그래프에서 0-트리의 도달가능상태는 T의 모든 열들의 일차결합으로 표현된다.

먼저 (i)에 대하여 첫 번째 행이 영벡터이므로 T_{M_n}e₁ ≠ e₁이다. 그런데 의 모든 열들의 일차결합으로 표현되지 않으므로 0-트리의 도달불가능 상태가 된다. 따라서 의 0-트리의 도달불가능한 상태이다.

(ii)는 (i)과 같은 방법으로 증명할 수 있다.

(iii)에서 은 1행과 2행이 같다. y를 라 하면 을 만족한다. 그런데 의 모든 열들의 일차결합으로 표현되지 않는다. 그리고 이므로 의 모든 열들의 일차결합으로 표현되지 않으므로 0-트리의 도달 불가능상태가 된다. 따라서 의0-트리의 도달불가능한 상태이다.

(iv)는 (iii)과 같은 방법으로 증명할 수 있다. □

<정리 3.3> 길이가 n인 LFSR 기반의 패턴분류기 의 상태전이행렬 에 대하여 DV는 다음과 같다.

증명> (i) 을 상태전이행렬로 갖는 의 상태 전이그래프에서 0-트리의 한 도달불가능상태는 정리 3.2에 의하여 x = (110 ⋯ 0)^t 이고 0-기본경로 는 (110 ⋯ 0)^t → (011 ⋯ 0)^t → ⋯ → (000 ⋯ 0)^t이다. 또한 0-기본경로의 성분을 각 행으로 하는 행렬 B₀는 식(6)과 같다.

따라서 N(B₀) = {(00 ⋯ 0)^t, (11 ⋯ 1)^t}이므로 정리 3.2에 의하여 DV = (1 ⋯ 1)이다.

(ii) , (iii), (iv)는 (i)과 같은 방법으로 증명할 수 있다.

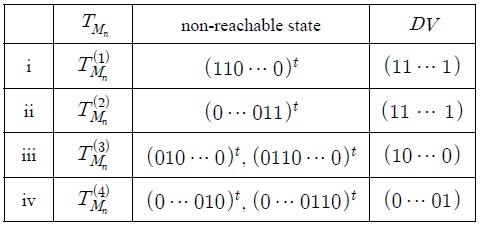
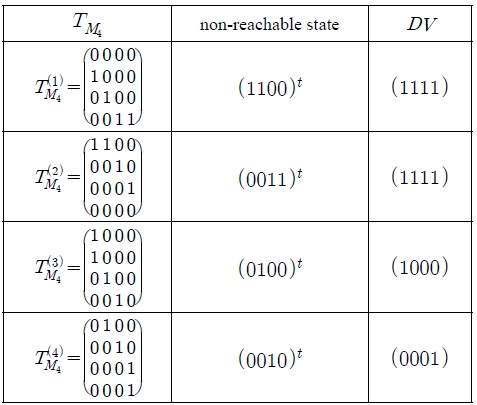
표 1은 n-셀 LFSR 기반의 패턴분류기 에 대하여 상태전이행렬 에 대응하는 상태전이 그래프에서 0-트리의 한 도달불가능한 상태와 의 DV를 나타낸다.

[표 1.] n-셀 LFSR 기반의 패턴분류기

n-셀 LFSR 기반의 패턴분류기

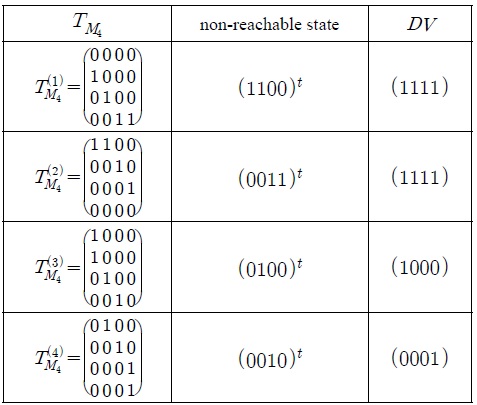
<예제 3.1> 길이가 4인 LFSR 기반의 패턴분류기 의 상태전이행렬이 이라 하자. 은 식(7)과 같고, 0이 아닌 끌개는 1이고 도달불가능상태는 정리 3.2에 의해 x = (1100)^t이다.

[그림 2.] 의 상태전이그래프

따라서 N(B₀) = {(0000)^t, (1111)^t}이므로 DV = (1111)이다.

길이가 4인 LFSR 기반의 패턴분류기 의 상태전이행렬 에 대하여 DV는 표 2와 같다.

[표 2.] n-셀 LFSR 기반의 패턴분류기 ？4M

n-셀 LFSR 기반의 패턴분류기 ？4M

Ⅳ. LFSR 기반의 패턴분류기 합성

이 절에서는 주어진 DV에 대응하는 LFSR 기반의 패턴분류기를 합성하는 방법을 제안한다.

[1,12]에서 언급한 인 경우와 DV = (0∗⋯∗0)인 경우를 제외하고 n-셀 DV에 대응하는 패턴분류기 의 상태전이행렬 T_{M_n}를 구성하는 방법이다. 다음 정리는 주어진 DV에 대응하는 LFSR 기반의 패턴분류기를 합성하는 방법이다.

<정리4.1> 길이가 n인 LFSR 기반의 패턴분류기 의 상태전이행렬 T_{M_n}에 대하여 n-셀 패턴분류기 의 상태전이행렬 T_{M_n}은 다음 표 3과 같다.

[표 3.] n-셀 LFSR 기반의 패턴분류기 ？nM

n-셀 LFSR 기반의 패턴분류기 ？nM

여기서 DV = (101) 인 패턴분류기 의 상태전이행렬 T_M_₃은 다음 식(4)과 같다.

증명> 정리 3.2에 의하여 도달불가능상태 x는 (110 ⋯ 0)^t이고 0-기본경로((110 ⋯ 0)^t → (0110 ⋯ 0)^t → ⋯ → (0 ⋯ 0110)^t → (0 ⋯ 010)^t → (0 ⋯ 001)^t의 성분을 각 행으로 하는 행렬 B₀는 식(9)과 같다.

N(B₀) = {(00 ⋯ 00)^t, (1 ⋯ 10)^t} 이므로 DV = (1 ⋯ 10 ⋯ 0)이다.

(ii), (iii), (iv), (v), (vi)의 경우 (i)과 같은 방법으로 증명할 수 있다.

<예제 4.1> (i) DV = (11110)인 LFSR 기반의 패턴분류기 의 상태전이행렬 T_M_₅은 식(10)과 같다.

(ii) DV = (11101)인 LFSR 기반의 패턴분류기 의 상태전이행렬 T_M_₅은 식(11)과 같다.

(iii) DV = (00101)인 LFSR 기반의 패턴분류기 의 상태전이행렬 T_M_₅은 식(12)와 같다.

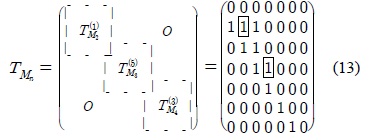
<예제 4.2> (i) DV = (1101000)인 LFSR 기반의 패턴분류기 의 상태전이행렬 T_M_₇은 식(13)과 같다.

(ii) DV = (1101000)인 LFSR 기반의 패턴분류기 의 상태전이행렬 T_M_₇은 식(14)와 같다.

다음은 LFSR 기반의 패턴분류기 합성에 대한 알고리즘이다.

[]

Ⅴ. 결 론

본 논문에서는 LFSR 기반의 패턴분류기를 생성하 였다. 생성한 LFSR 기반의 패턴분류기의 분석을 통해 상태전이그래프에서 0-트리의 한 도달불가능상태를 찾 는 방법을 제안하였고 이를 통해 DV를 구하는 시간을 효과적으로 줄였다. 또한 주어진 길이가 n인 DV에 대응하는 LFSR 기반의 패턴분류기 의 상태전이행렬 T_{M_n}을 기본형이 되는 T_{M_i}를 합성하여 생성하는 방법을 제안하였다.

참고문헌

1. Ganguly N. 2003 “Cellular Automata Evolution: Theory and Applications in Pattern Recognition and Classification,”
2. Krishna C., Jas A., Touba N.A. 2004 “Achieving high encoding efficiency with partial dynamic LFSR reseeding,” [ACM Trans. Design Automation of Electronic Systems] Vol.9 P.500-516
3. Maji P., Shaw C., Ganguly N., Sikdar B.K., Chaudhuri P.P. 2003 “Theory and application of cellular automata for pattern classification,” [Fundamenta Informaticae] Vol.58 P.321-354
4. Krishna C., Jas A., Touba N.A. 2004 “Achieving high encoding efficiency with partial dynamic LFSR reseeding,” [ACM Trans. Design Automation of Electronic Systems] Vol.9 P.500-516
5. Krishna C.C., Touba N.A. 2002 “Reducing test data volume using LFSR reseeding with seed compression,” [in Proc. IEEE ITC] P.321-330
6. Golomb S. 1967 Shift Register Sequences
7. Lidl R., Niederreiter H. 1997 Finite Fields
8. Das A.K., Chaudhuri P.P. 1993 “Vector space theoretic analysis of additive cellular automata and its application for pseudo-exhaustive test pattern generation,” [IEEE Trans. Comput-Aided Des. Integr. Circuits Syst.] Vol.42 P.340-352
9. Chaudhuri P.P., Chowdhury D.R., Nandy S., Chattopadhyay C. 1997 Additive Cellular Automata; Theory and Applications
10. Cho S.J., Choi U.S., Kim H.D. 2002 “Behavior of complemented cellular automata derived from a linear cellular automata,” [Mathematical and Computer Modelling] Vol.36 P.979-986
11. Strang G. 2009 Introduction to Linear Algebra
12. Cho S.J., Kim H.D., Choi U.S., Kim S.T., Kim J.G., Kwon S.H., Gong G.T. 2014 “Generation of TPMACA for Pattern Classification,” [LNCS] Vol.8751 P.408-416