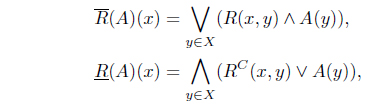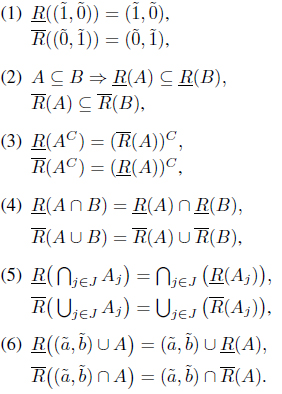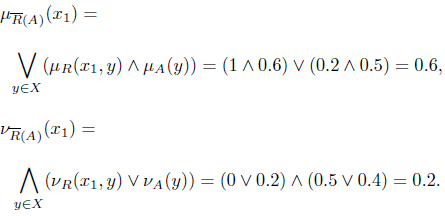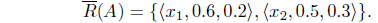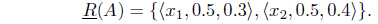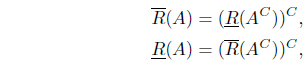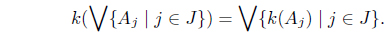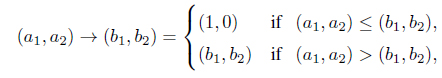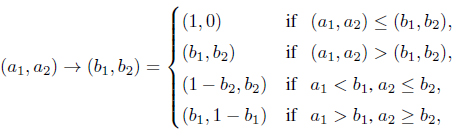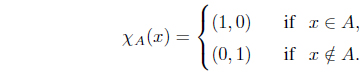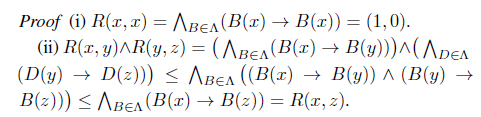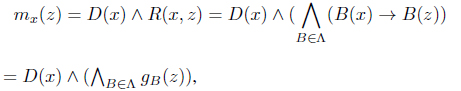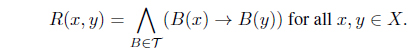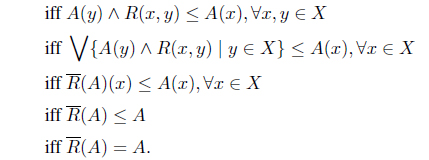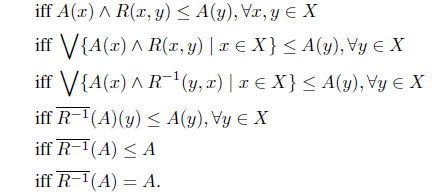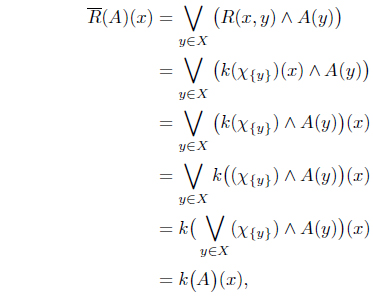Let X be a nonempty set. An intuitionistic fuzzy set A is an ordered pair
A = (µA, νA).
where the functions µA : X → I and νA : X → I denote the degree of membership and the degree of nonmembership, respectively and µA +νA ≤ 1 (See [9]). Obviously every fuzzy set µ in X is an intuitionistic fuzzy set of the form .
Throughout this paper, I ⊗ I denotes the family of all intuitionistic fuzzy numbers (a, b) such that a, b ∈ [0, 1] and a + b ≤ 1, with the order relation defined by
(a, b) ≤ (c, d) iff a ≤ c and b ≥ d.
And IF(X) denotes the family of all intuitionistic fuzzy sets in X, and ‘IF’ stands for ‘intuitionistic fuzzy.’
Any IF set A = (µA, νA) on X can be naturally written as a function A : X → I ⊗ I defined by A(x) = (µA(x), νA(x)) for any x ∈ X.
For any IF set A = (µA, νA) of X, the value
πA(x) = 1 − µA(x) − νA(x)
is called an indeterminancy degree (or hesitancy degree) of x to A (See [9]). Szmidt and Kacprzyk [10] call πA(x) an intuitionistic index of x in A. Obviously
0 ≤ πA(x) ≤ 1, ∀x ∈ X.
Note πA(x) = 0 iff νA(x) = 1 − µA(x). Hence any fuzzy set µA can be regarded as an IF set (µA, νA) with πA = 0.
Definition 2.1 ( [11]). An IF set R on X × X is called an IF relation on X. Moreover, R is called
(i) reflexive if R(x, x) = (1, 0) for all x ∈ X, (ii) symmetric if R(x, y) = R(y, x) for all x, y ∈ X, (iii) transitive if R(x, y) ∧ R(y, z) ≤ R(x, z) for all x, y, z ∈ X.
A reflexive and transitive IF relation is called an IF preorder. A symmetric IF preorder is called an IF equivalence. An IF preorder on X is called an IF partial order if for any x, y ∈ X, R(x, y) = R(y, x) = (1, 0) implies that x = y. In this case, (X, R) is called an IF partially ordered space. An IF preorder R is called an IF equality if R is both an IF equivalence and an IF partial order.
Remark 2.2. R−1 is called the inverse of R if R−1 (x, y) = R(y, x) for any x, y ∈ X. If R is an IF preorder, so is R−1 . RC is called the complement of R if RC (x, y) = (νR(x,y) , µR(x,y)) where R(x, y) = (µR(x,y) , νR(x,y)). It is obvious that R−1 ≠ RC .
Definition 2.3 ( [12]). Let R be an IF relation on X. Then the two functions , : IF(X) → IF(X), defined by
are called the upper approximation operator and the lower approximation operator on X, respectively. Moreover, (X, R) is called an IF approximation space.
For any IF number (a, b) ∈ I ⊗ I, is an IF set which has the membership value a constant ”a” and the nonmembership value a constant ”b” for all x ∈ X.
Proposition 2.4 ( [12, 13]). Let (X, R) be an IF approximation space. Let A, B ∈ IF(X), {Aj | j ∈ J} ⊆ IF(X) and (a, b) ∈ I ⊗ I. Then we have
Theorem 2.5 ( [12, 13]). Let (X, R) be an IF approximation space. Then
(1) R is reflexive
(2) R is transitive
Theorem 2.6. Let (X, R) be a reflexive IF approximation space. If for each j ∈ J, then .
Proof By the reflexivity of R and Theorem 2.5, . By Proposition 2.4,
Thus .
Example 2.7. Let X = {x1, x2}. Let R = {<(x1, x1), 1, 0>, <(x1, x2), 0.2, 0.5>,<(x2, x1), 0.4, 0.3>,<(x2, x2), 1, 0>}. Then (X, R) is an IF approximation space. Let A = {<x1, 0.6, 0.3>, <x2, 0.5, 0.4>} be an IF set on X, then
Similarly, we obtain
Hence,
Similarly, we have
Proposition 2.8 ( [12]). For an IF relation R on X and A ∈ IF(X), the pair and are “dual”, i.e.,
where AC is the complement of A.
Definition 2.9 ( [13, 14]). An IF topology T on X in the sense of Lowen [15] is a family of IF sets in X that is closed under arbitrary suprema and finite infima, and contains all constant IF sets. The IF sets in T are called open, and their complements, closed.
Definition 2.10 ( [8]). A Kuratowski IF closure operator on X is a function k : IF(X) → IF(X) satisfying for (a, b) ∈ I ⊗ I, A, B ∈ IF(X),
(i) , (ii) A ≤ k(A), (iii) k(A ∨ B) = k(A) ∨ k(B), (iv) k(k(A)) = k(A).
A Kuratowski IF closure operator k on X is called saturated if for all Aj ∈ IF(X), j ∈ J,
Furthermore, an IF topology is called saturated if it has a saturated IF closure operator.
Remark 2.11 ( [13]). Every Kuratowski IF closure operator k on X gives rise to an IF topology on X in which an IF set B is closed iff k(B) = B.
Generally, for (a1, a2),(b1, b2) ∈ I ⊗ I, the implication operator (or residual implicator) [16, 17] is defined as follows;
(a1, a2) → (b1, b2) = sup{(d1, d2) ∈ I ⊗ I | (a1, a2) ∧ (d1, d2) ≤ (b1, b2)}.
If given IF numbers (a1, a2),(b1, b2) are comparable, then the IF implication operator is clearly given by
for all (a1, a2),(b1, b2) ∈ I ⊗ I.
But it is not always able to compare given IF numbers. Nevertheless, in many papers the IF implication operator is studied where given IF numbers are comparable. In this paper, we consider the IF implication operator to the extend that the given IF numbers are not comparable with some restrictions.
Remark 3.1. The IF residual implicator is clearly given by
for all (a1, a2),(b1, b2) ∈ I ⊗ I.
Definition 3.2. (1) For (a1, a2) ∈ I ⊗ I, A ∈ IF(X) and x ∈ X, the map ((a1, a2) ∧ A) : I ⊗ I × IF(X) → IF(X) is defined by
((a1, a2) ∧ A)(x) = (a1, a2) ∧ A(x).
(2) For (a1, a2) ∈ I ⊗ I, A ∈ IF(X) and x ∈ X, the map ((a1, a2) → A) : I ⊗ I × IF(X) → IF(X) is defined by
((a1, a2) → A)(x) = (a1, a2) → A(x).
(3) For A, B ∈ IF(X), the map (A → B) : IF(X) × IF(X) → IF(X) is defined by
(A → B)(x) = A(x) → B(x), ∀x ∈ X.
Remark 3.3. (1) We denote by [(a1, a2),(1, 0)] the rectangular plane which represents [a1, 1]×[0, a2]. For a set A ⊆ X, an IF set χA : X → I ⊗ I is a map defined by
From the above, if (a1, a2) ∈ I ⊗ I and A ∈ IF(X) are comparable, then we have that
(a1, a2) → A = χA−1[(a1, a2),(1,0)] ∨ A.
(2) If (a1, a2),(b1, b2),(c1, c2) ∈ I ⊗ I are all comparable, then
(a1, a2) ∧ (b1, b2) ≤ (c1, c2) iff (b1, b2) ≤ (a1, a2) → (c1, c2).
Clearly the following holds;
((a1, a2) → (b1, b2)) ∧ ((b1, b2) → (c1, c2)) ≤ ((a1, a2) → (c1, c2)).
Theorem 3.4. The implication operator ”→” is an IF preorder on I ⊗ I.
Proof By the above property and the fact
(a1, a2) → (a1, a2) = (1, 0),
it follows.
Let (X, ≤) be a preordered space and A ⊆ X. Let ↑ A = {y ∈ X | y ≥ x, for some x ∈ A}. If ↑ A = A, then A is called an upper set. Dually if B =↓ B = {y ∈ X | y ≤ x, for some x ∈ B}, then B is called a lower set. The family of all the upper sets of X is clearly a topology on X, which is called the Alexandrov topology (See [18]) on X, and denoted Γ(≤). We write simply Γ(X) for the topological space (X, Γ(≤)).
On the other hand, for a topological space (X, T) and x, y ∈ X, let x ≤ y if x ∈ U implies y ∈ U for any open set U of X, or equivalently, . Then ≤ is a preorder on X, called the specialization order (See [18]) on X. Denote this preorder by Ω(T). We also write simply Ω(X) for (X, Ω(T)).
A function f : (X, ≤1) → (Y, ≤2) between two preordered sets is called order-preserving if x ≤1 y implies f(x) ≤2 f(y).
From now on we are going to enlarge the above ideas to the IF theories in a natural way.
Definition 4.1. Let (X, R) be an IF preordered space. Then A ∈ IF(X) is called an IF upper set in (X, R) if
A(x) ∧ R(x, y) ≤ A(y), ∀x, y ∈ X.
Dually, A is called an IF lower set if A(y) ∧ R(x, y) ≤ A(x) for all x, y ∈ X.
Let R be an IF preorder on X. For x, y ∈ X, the real number R(x, y) can be interpreted as the degree to which x is less than or equal to y. The condition A(x) ∧ R(x, y) ≤ A(y) can be interpreted as the statement that if x is in A and x ≤ y then y is in A. Particularly, if R is an IF equivalence relation, then an IF set A is an upper set in (X, R) if and only if it is a lower set in (X, R).
The classical preorder relation x ≤ y can be naturally extended to R(x, y) = (1, 0) in IF preorder relation. Since (1, 0) = R(x, y) ≤ A(x) → A(y), A(x) ≤ A(y) for any IF upper set A. That is, x ≤ y means A(x) ≤ A(y). Obviously, the notion of IF upper sets and IF lower sets agrees with that of upper sets and lower sets in classical preordered space.
Definition 4.2. A function f : (X, R1) → (Y, R2) between IF preordered spaces is called order-preserving if
R1(x, y) ≤ R2(f(x), f(y)), ∀x, y ∈ X.
Definition 4.3. Let X be a totally ordered set. An IF set A on X is called
(i) increasing if for all x, y ∈ X with x < y, A(x) ≤ A(y), (ii) decreasing if for all x, y ∈ X with x < y, A(x) ≥ A(y), (iii) monotone if A is increasing or decreasing.
Definition 4.4. Let A = (µA, νA) be an IF set. A is called simple if µA or νA is a constant function.
Remark 4.5. (1) If indeterminancy degree πA is a constant function t, then for any two different elements x, y ∈ X, πA(x) = πA(y) = t. So, if µA(x) ≤ µA(y), then νA(x) ≥ νA(y). Hence A(x) ≤ A(y). Therefore A(x) and A(y) are comparable for any x, y ∈ X provided that the hesitancy degree of an IF set A is a constant function.
(2) Suppose that the universal set X is a totally ordered set. If A is monotone or simple, then A(x) and A(y) are comparable for any different element x, y ∈ X.
From now on, in order to avoid getting imprecise value in acting with the implication operator, we will consider only the IF set A : X → I ⊗ I such that A(x) and A(y) are comparable for any x, y ∈ X. By Remark 4.5, any function which is monotone or simple or of constant hesitancy degree is an example of such function.
Lemma 4.6. For a given IF preordered space (X, R), an IF set B : X → I ⊗ I is an IF upper set of (X, R) if and only if B : (X, R) → (I ⊗ I, →) is an order-preserving function.
Proof For any B ∈ IF(X), we have the following relations.
B is an IF upper set in (X, R)
⇔ B(x) ∧ R(x, y) ≤ B(y) for all x, y ∈ X ⇔ R(x, y) ≤ B(x) → B(y) for all x, y ∈ X ⇔ The map B : (X, R) → (I ⊗ I, →) defined by preserves order.
Theorem 4.7. If (X, R) is an IF preordered space, then the family T of all the upper sets in X satisfies the following conditions, and hence it is an IF topology on X.
For any IF sets Aj , A ∈ T ;
(i) , (ii) , (iii) , (iv) , (v) Suppose that for any A ∈ T and x, y ∈ X and (a, b) ∈ I ⊗ I, A(x) and A(y) and (a, b) are all comparable. Then ((a, b) → A) ∈ T .
Proof (i) Let (a, b) ∈ I ⊗ I, then . So .
(ii) .
(iii) .
(iv) If A is an upper set, then A(x) ∧ R(x, y) ≤ A(y) for any x, y ∈ X. So, we obtain that
((a, b) ∧ A(x)) ∧ R(x, y) ≤ ((a, b) ∧ A(y)),
for all (a, b) ∈ I ⊗ I. This means that ((a, b) ∧ A) ∈ T .
(v) By Remark 3.3, ((a, b) → A(x)) ∧ (A(x) → A(y)) ≤ ((a, b) → A(y)). Thus((a, b) → A(x)) → ((a, b) → A(y)) ≥ (A(x) → A(y)) ≥ R(x, y). Hence ((a, b) → A(x)) ∧ R(x, y) ≤ ((a, b) → A(y)).
Definition 4.8. For an IF preordered space (X, R), let
If T is a family of IF sets in X which satisfies conditions (i)-(v) of Theorem 4.7, then there exists an IF preorder R on X such that T consists of all the upper sets of the IF preordered space (X, R). It will be shown in the following theorem.
Lemma 4.9. Let Λ be a subfamily of IF(X) such that for any A ∈ Λ and for any x, y ∈ X, A(x) and A(y) are comparable. Let . Then R is an IF preorder.
Theorem 4.10. Let Λ be a subfamily of IF(X) satisfying (i)-(v) of Theorem 4.7 such that for any A ∈ Λ and for any x, y ∈ X, A(x) and A(y) are comparable. Then there exists an IF preorder R such that Λ is the family T of all upper sets in X with respect to R.
Proof Suppose that Λ ⊆ IF(X) satisfy the conditions (i)-(v) of Theorem 4.7. Define . By the above lemma, R is an IF preorder on X. Let B ∈ Λ. Since B(x) and B(y) are comparable for any x, y ∈ X, we have R(x, y) ≤ B(x) → B(y). Hence B(x) ∧ R(x, y) ≤ B(y), i.e. B is an IF upper set. Thus Λ ⊆ T .
What remains is to show that T ⊆ Λ. Take D ∈ T . For a given x ∈ X, define mx : X → I ⊗ I by mx(z) = D(x) ∧ R(x, z) for all z ∈ X. Then mx(x) = D(x) and mx(z) ≤ D(z) for all z ∈ X. Thus .
For each B ∈ Λ and previously given x, define gB : X → I ⊗ I by gB(z) = B(x) → B(z) for all z ∈ X. By (v), gB ∈ Λ. By (iii), we obtain that . Since
we have mx ∈ Λ. Note that . Therefore D ∈ Λ by (ii).
Example 4.11. Let X = [0, 1] be the universal set. Let Λ be the family of all constant IF sets on X and the IF set A = (µA, νA), where µA(x) = 1−x, νA(x) = x. Take Γ by arbitrary suprema and arbitrary infima with members of Λ. Then clearly Γ ⊆ IF(X) and it satisfies (i)-(v) of Theorem 4.7. We can define the order R on X by
Then clearly R is reflexive. Take x, y ∈ X such that x ≤ y, then R(x, y) = A(y) and R(y, x) = (1, 0). So we know that R is transitive. Therefore R is a preorder on X. Consider A(x)∧ R(x, y) when x ≤ y. Then R(x, y) = A(y), and hence A(x) ∧ R(x, y) = A(x) ∧ A(y) ≤ A(y). Consequently we know that Γ is the family of all upper sets in X with respect to R.
The following result relates lower sets and upper sets in an IF preordered space (X, R) with the upper approximation operator and , respectively.
Proposition 4.12. Let (X, R) be an IF preordered space and A ∈ IF(X). Then A is a lower set iff .
Proof A is a lower set
Proposition 4.13. Let (X, R) be an IF preordered space and A ∈ IF(X). Then A is an upper set iff .
Proof A is an upper set
Remark 4.14. Let T be the family of all upper sets of an IF preordered space (X, R). By Theorem 4.7, T is an Alexandrov IF topology on X. Furthermore by the above proposition.
Proposition 4.15. Let (X, R) be an IF preordered space. Then is an Alexandrov IF topology on X.
Proof (1) Take (a, b) ∈ I ⊗ I, then we know that . So . Clearly . Hence . Therefore for any (a, b) ∈ I ⊗ I.
(2) Take . Then for each j ∈ J. So . Thus .
(3) Take . Then for each j ∈ J. So . Thus .
Remark 4.16. The IF topology is dual to the IF topology . It follows from the fact that for . In addition, the IF topologies and are Alexandrov IF topologies.
Proposition 4.17. Let (X, R) be an IF preordered space and A ∈ IF(X). Then
(i) is the IF interior operator for the IF topology , (ii) is the IF closure operator for the IF topology .
Proof (i) We will show that for any A ∈ IF(X). Since , . Since , . By Theorem 2.6, . So . On the other hand, by , we obtain . Hence . Therefore .
(ii) We will show that for any A ∈ IF(X). Since , . By the duality, . Hence .
Proposition 4.18. Let k be a saturated IF closure operator on X. Then there exists an IF preorder R on X such that k = iff
(i) for any Aj ∈ IF(X), and (ii) k((a, b) ∧ A) = (a, b) ∧ k(A) for any A ∈ IF(X) and (a, b) ∈ I ⊗ I.
Proof Suppose that k satisfies (i) and (ii). By using k, we define an IF relation R on X as
R(x, y) = k(χ{y})(x), x, y ∈ X.
For each A ∈ IF(X), if x ≠ y, we have
(χ{y}∧A(y))(x) = (χ{y})(x)∧A(y) = (0, 1)∧A(y) = (0, 1).
So , hence .
For every x ∈ X, we have
which implies .
Conversely suppose the assumptions. Since k is a Kuratowski IF closure operator, T = {AC ∈ IF(X) | k(A) = A} is an IF topology T on X, and it satisfies (i). By Lemma 4.9, there exists an IF preorder R on X with respect to the family T . Since , k satisfies (ii) by Proposition 2.4.