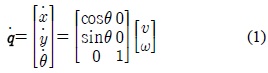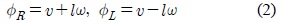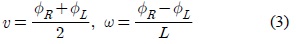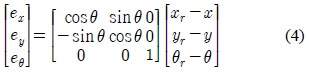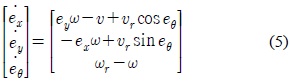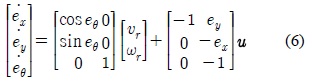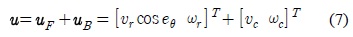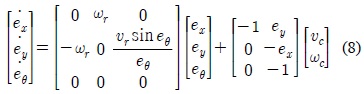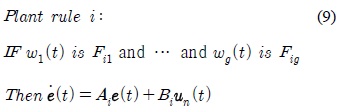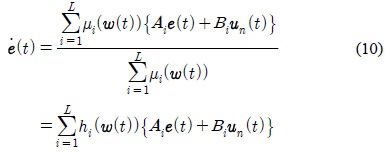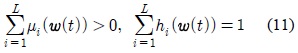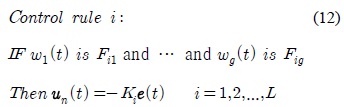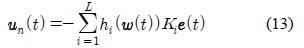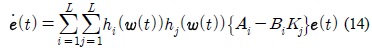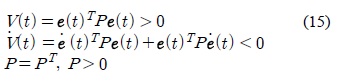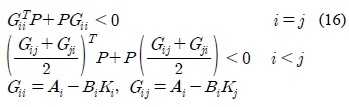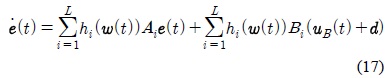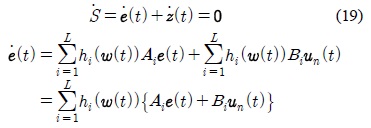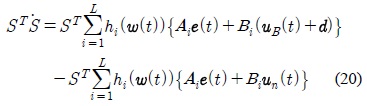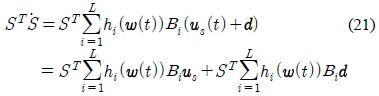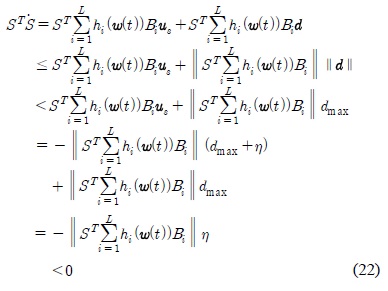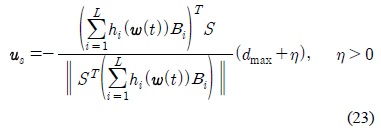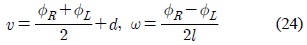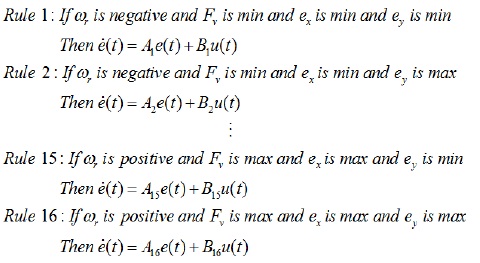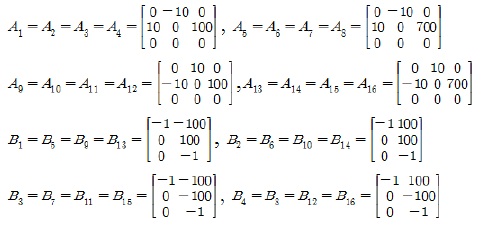In this paper, a robust trajectory tracking control method of a wheeled mobile robot is newly proposed combining the PDC and the ISMC. The PDC is a relatively simple and easy control method for nonlinear system compared to the other non-linear control methods. And the ISMC can have robust and stable control characteristics against model uncertainties and disturbances from the initial time by placing the states on the sliding plane with desired nominal dynamics. Therefore, the proposed PDC+ISMC trajectory tracking control method shows robust trajectory tracking performance in spite of external disturbance. The tracking performance of the proposed method is verified through simulations. Even though the disturbance increases, the proposed method keeps the performance of the PDC method when there is no disturbance. However, the PDC trajectory tracking control method has increasing tracking error unlike the proposed method when the disturbance increases.
이동 로봇의 궤도 추적 제어(trajectory tracking control) 문제는 이동 로봇의 자율 주행에 있어 중요한 주제로서 이동 로봇으로 하여금 주어진 기준 궤도를 따라가게 하는 것을 목표로 한다. 이동 로봇의 기준 궤도추적에 있어 기준 궤도와 이동로봇의 에러 동특성은 비선형 시스템이다. 이러한 비선형 시스템의 제어를 위한 기법들이 지금까지 많이 소개되어 왔다[1].
그 중에서, 일반적으로 많이 사용되는 방법 중의 하나가 T-S 퍼지 제어 기법이다[2]. 이러한 T-S 퍼지 제어기법 중에서 일반적으로 다른 방법에 비해 상대적으로 간단하고 사용하기 쉬운 PDC (Parallel Distributed Compensation)라는 제어 기법이 많이 사용된다. PDC 제어 기법은 선형 모델의 결합으로 나타낸 T-S 퍼지 모델에 선형 제어 기법의 하나인 상태 궤환 제어를 사용하며, 설계 과정에서 Lypunov 안정 조건을 이용하여 전체 제어 시스템의 안정도를 보장 받는다[3,4]. 이 기법은 다른 비선형 제어 기법이나 T-S 퍼지 제어 기법들에 비하여 보다 간단한 방법으로 제어를 할 수 있다는 장점이 있지만, 입력 신호에 외란이 존재하는 경우 제어 성능 면에 있어 다른 복잡한 제어 기법들에 비하여 부족함이 있다. 그렇기 때문에 외란이 있는 경우 PDC를 이용해 정확한 제어를 하기 위해서는 이 점을 보완할 방법이 필요하다.
시스템의 불확실성과 외란에 강인한 제어 기법의 하나로서 슬라이딩 모드 제어(sliding mode control) 기법[5]이 있는데, 이 기법은 시스템의 구조를 변경하여, 시스템의 상태를 슬라이딩 평면상에 구속시킴으로써 강인성을 얻을 수 있는 비선형 제어 기법이다. 그러나, 슬라이딩 모드 제어 기법은 도달 모드(reaching mode)에서 외란에 영향을 받을 수 있는 단점이 있다. 이 단점을 보완하고자 도달 모드가 존재하지 않고 초기시간부터 슬라이딩 모드가 존재하는 적분 슬라이딩 모드 제어(ISMC : Integral Sliding Mode Control:) 기법이 제안되었다[6,7]. 이는 공칭 시스템에 대해서 공칭 제어 입력을 미리 결정해 놓고 그 공칭 시스템의 응답 특성과 같은 동특성을 갖도록 슬라이딩 평면을 결정하는 방법이다. 다시 말해 적분 슬라이딩 모드 제어기는 슬라이딩 평면에 동특성을 부여하여 도달 모드를 제거함으로써전 영역에서 모델의 불확실성과 외란에 강인한 특성을 보여주는 제어기로서, 초기시간부터 오차 동력학에서의 궤적이 슬라이딩 평면에 있게 하며, 적절한 제어 입력에 의해 지속적으로 그 평면상에 머물러 있도록 하여 외란이 있는 경우에도 공칭계통의 동특성을 유지할 수있도록 한다. 한편, 이동로봇의 궤도 추적 제어를 위하여 Lyapunov 함수를 이용해 안정도를 보장 받는 제어기가 제안되었고, 이동 로봇의 궤적과 기준궤적 간의 오차 방정식을 제어 시스템으로 놓고 그 오차 값을 평형 상태로 보내어 오차를 0으로 만드는 궤도 추적 제어방법이 제안되었다[8]. 그리고 제어 입력이 피드포워드 입력과 피드백 입력으로 구성되어진 구조의 제어 시스템을 가지며, 기준 궤도 주위에서 선형화된 에러 동특성을 가지는 모델에 선형 예측 제어 기법을 적용하여 제어기를 설계하는 궤도 추적 제어 방법이 제안되었다[9]. 근래에는 [9]에서 제시된 기준 궤도 주위에서 선형화된 에러 동특성 모델에 다항식 퍼지 모델링과 제곱합 (sum of squares) 기법을 사용하여 작은 제어 입력을 갖는 제어기를 설계하는 궤도 추적 제어 방법이 제안되었다[10]. 또한, 기준 궤도 주위에서의 선형화 없이 비선형 에러 동특성 모델에 직접 PDC 기법을 적용하여 제어기를 설계하는 궤도 추적 제어 방법이 제안되었다[11,12]. 이와 함께, 드리프트(drift) 불확실성을 갖는 이동 로봇의 안정적이고 강인한 궤도 추적을 위하여 적분 슬라이딩 모드 제어 기법을 적용한 추적 방법이 제시되었으며[13], 모델링 불확실성과 외란이 존재할 때 이동 로봇의 효과적인 궤도 추적 제어를 위하여 슬라이딩 모드 이론과 신경망 보상기를 이용한 궤도 추적 방법이 제시되었다[14]. 그러나 이 방법들은 제어기 설계가 간단하지 않거나 실시간으로 사용하는데 문제가 있다. 따라서, 본 논문에서는 일반적인 PDC 기법에 ISMC 기법을 결합하여 위의 방법에 비해 상대적으로 간단하고 실용적인 외란에 강인한 궤도 추적 제어 방법을 새롭게 제안하기로 한다.
본 연구에서는 [9]에서 제시된 궤도 추적 제어 시스템에 PDC 기법과 ISMC 기법을 결합하여 피드백 제어입력을 설계함으로써 외란이 있는 경우에도 공칭 계통의 동특성을 유지할 수 있도록 한다. 즉, 이동 로봇에 외란이 가해지더라도 외란이 없는 경우의 PDC 제어 기법에 의한 궤도 추적 성능을 유지하도록 하는 강인한 궤도 추적 방법을 제안한다. 이를 위하여, 먼저 비선형 시스템인 이동로봇의 주행 궤도와 기준궤도 간의 에러 동특성 방정식을 T-S 퍼지 모델링 한 후 Lyapunov 안정조건 및 LMI 연산을 이용해 상태 궤환 이득을 구하여 공칭 시스템의 동특성을 갖도록 하는 공칭 제어 입력을 얻는다. 그런후, T-S 퍼지 모델에 ISMC 기법을 적용하여 외란이 있는 경우에도 공칭계통의 동특성을 유지할 수 있도록 하는 불연속 제어 입력을 얻는다. 또한, matlab/simulink 시뮬레이션을 통해 본 논문에서 제안한 궤도 추적 방법을 검증하기로 한다. 외란이 있는 경우, PDC 제어 입력만을 사용한 경우와 PDC 제어 입력에 ISMC로부터 설계한 제어 입력을 추가한 경우를 비교함으로써 제안한 궤도 추적 방법의 성능을 증명하도록 한다.
본 논문의 구성은 다음과 같다. Ⅱ절의 2.1절 에서는 바퀴형 이동로봇의 기구학 모델과 궤도 추적을 위한 에러 동특성 방정식에 대해 기술한다. 그리고 2.2절에서는 제안하는 PDC와 ISMC를 결합한 강인 궤도 추적 제어기의 제어 입력 설계 방법에 대하여 기술하고, 2.3절에서는 시뮬레이션 결과를 보여준다. 마지막으로 Ⅲ절에 결론을 기술한다.
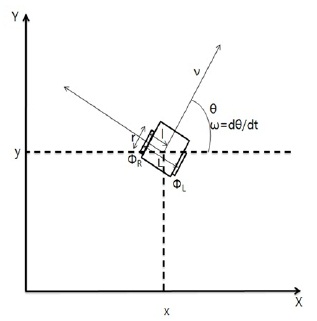
이동로봇이 그림 1 과 같이 지면의 굴곡이 없는 평면 좌표계
위의 식 (1)에서
이동로봇의 오른쪽 바퀴와 왼쪽 바퀴의 속도를 각각
여기서 이며 이동로봇의 중심으로부터 바퀴까지의 거리이다. 식 (2)를
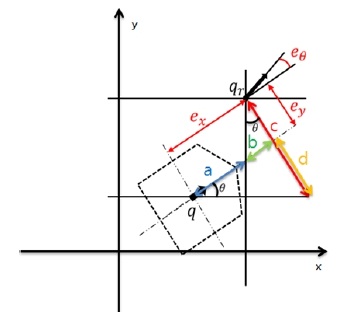
그림 2는 이동로봇과 기준궤도의 자세 오차를 보여 주고 있는데,
위의 식 (4)를 시간에 대해 미분을 하면, 다음 식 (5)와 같은 방정식을 얻을 수 있다.
식 (5)는 식 (6)과 같이 다시 나타낼 수 있다.
여기서
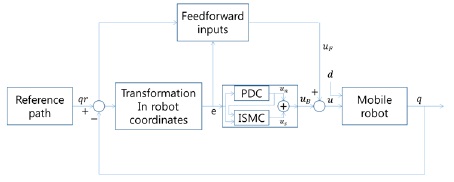
그림 3은 본 논문에서 사용한 이동 로봇의 전체적인 궤도 추적 제어 시스템의 구조 이다. 이동로봇의 입력 벡터 즉 제어 입력 벡터
위의 식 (7)을 식 (6)에 대입하면 다음의 식 (8)과 같은 이동 로봇의 기준궤도 추적 제어를 위한 에러 동특성 방정식을 얻을 수 있다[10-12].
2.2. PDC와 ISMC를 결합한 궤도 추적 제어기 설계
본 논문에서는 위의 식 (8)에 PDC 기법과 ISMC 기법을 적용하여 외란에 대해 강인하면서 정확한 궤도 추적 성능을 갖는 이동 로봇의 궤도 추적 제어기를 제안하기로 한다.
2.2.1. PDC를 이용한 제어 입력
PDC 기법[3,4]은 선형 시스템의 결합으로 표현된 T-S 퍼지 모델에 Lyapunov 안정 조건을 이용하여 상태 궤환 이득을 구한 후 각 규칙의 적합도를 반영해서 결합한 상태 궤환 제어 입력으로 전체 시스템을 제어하는 기법이다.
Takagi와 Sugeno에 의해서 제안된 T-S 퍼지 모델은 비선형 시스템을 여러 개의 선형 모델들의 결합으로 표현한다.
식 (8)에 대한 T-S 퍼지 모델의
여기서
PDC 제어 기법의 퍼지 제어 규칙은 다음 식 (12)와 같은 형태를 가지며, 전체 제어 입력은 식 (13)과 같이 추론된다. 여기서,
식 (13)을 식 (10)에 대입하면, 전체 제어 시스템은 다음 식 (14)처럼 된다.
위의 식 (14)에 식 (15)와 같은 Lyapunov 안정 조건을 적용하여
2.2.2. ISMC를 이용한 제어 입력
적분 슬라이딩 모드 제어(ISMC) 기법[6,7]은 초기시간부터 오차 동력학에서의 궤적이 슬라이딩 평면에 있게 하며, 적절한 제어입력에 의해 지속적으로 그 평면상에 머물러 있도록 하여 외란이 있는 경우에도 공칭계통의 동특성을 유지할 수 있도록 한다.
그림 3의 궤도 추적 제어 시스템에서, 외란
ISMC의 슬라이딩 평면은 다음과 같이 선정한다.
식 (20)에서
여기서, 외란의 크기를 ||
여기서,
여기서는 matlab / simulink를 이용한 시뮬레이션을 통하여 제안된 궤도 추적 제어 방법의 추적 성능을 확인한다.
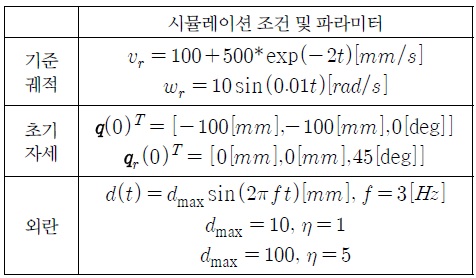
식 (6)의 에러 동특성 방정식을 이용하여 2.2절에서 제시된 궤도 추적 방법에 의해 이동 로봇의 궤도 추적 제어기를 설계하고 시뮬레이션을 통하여 궤도 추적 성능을 살펴보았다. 시뮬레이션은 matlab / simulink로 수행하였으며, 기준 궤적의 선속도
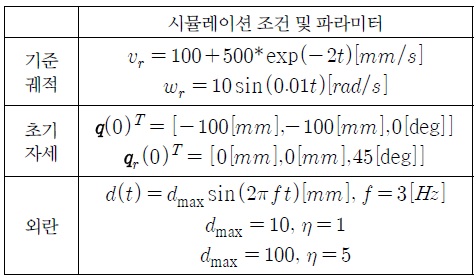
시뮬레이션 조건 및 파라미터
외란
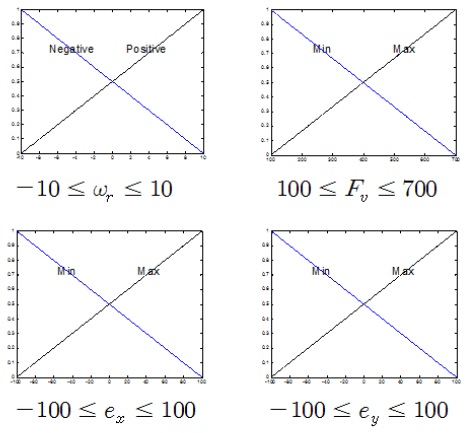
제어기 설계를 위해서 먼저 식 (8)에 대한 T-S 퍼지 모델링이 필요하다. 먼저 식 (8)의 비선형 성분을 전건부 변수로 선정하여 그에 따른 소속 함수를 정하고, T-S 퍼지 모델링을 위한 퍼지 규칙을 만든다. 그림 4와 같이식 (8)의 네 가지 비선형 성분에 대해 각각 두 가지 경우의 소속 함수를 정하였다. 각 전반부 변수의 범위는 실제 파라미터의 변동 범위를 고려하여 선정하여야 한다. 여기서는 기준 궤적의 입력의 범위와 오차의 변동 범위에 따라 전반부 변수들의 범위를 결정하였다.
이렇게 결정된 소속 함수들을 이용해 퍼지 규칙을 정하게 되는데, 본 논문에서는 각 네 변수의 두 가지 경우를 이용하여 총 16 가지의 규칙을 다음 그림 5와 같이 정하였다. 그림 4와 그림 5에서 이다.
각 규칙의 후반부 선형 모델에 대한
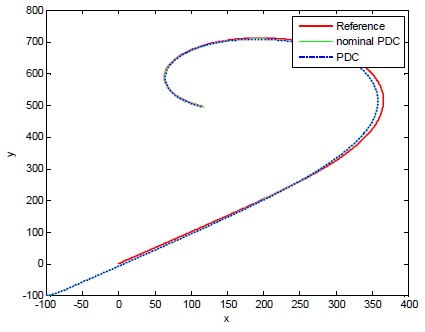
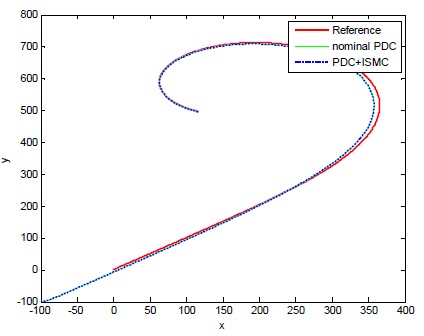
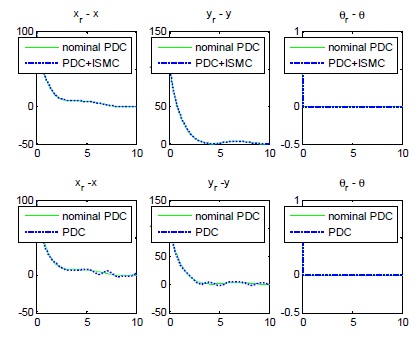
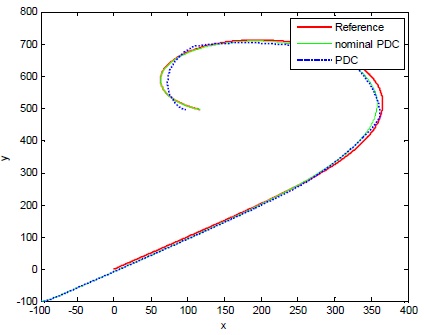
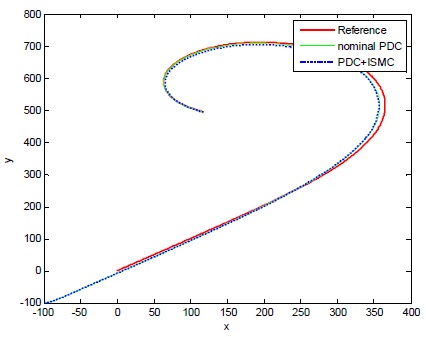
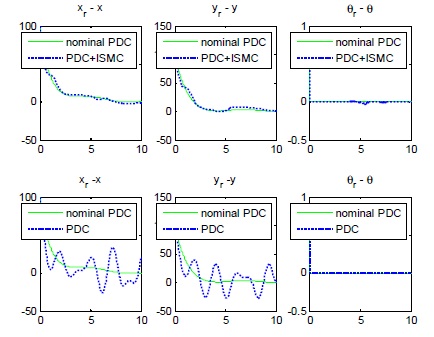
그림 7과 8은 각각
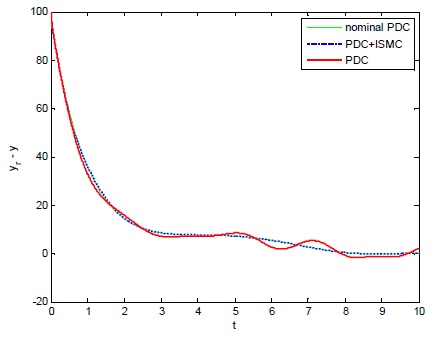
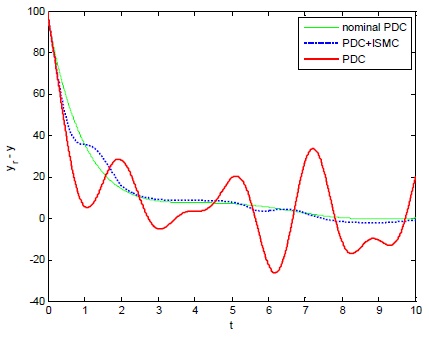
정량적인 차이를 좀 더 보기 쉽게 살펴보기 위하여, 그림 9와 그림 13에 대해서
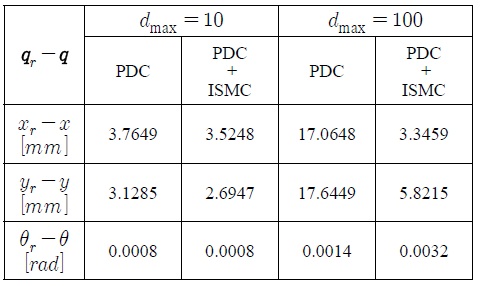
[표 2.] PDC와 PDC+ISMC 제어기의 궤도 추적 오차의 r.m.s. 값 비교
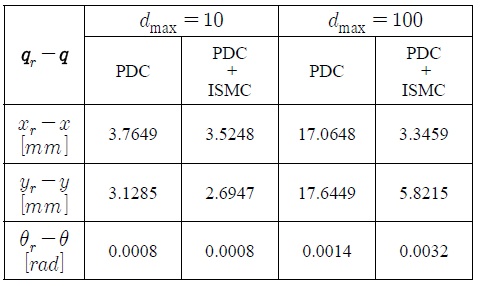
PDC와 PDC+ISMC 제어기의 궤도 추적 오차의 r.m.s. 값 비교
표 2를 살펴보면 외란이
본 논문에서는 바퀴형 이동 로봇의 궤도 추적 제어를 위하여 PDC 기법에 ISMC 기법을 추가하여 외란에 강인한 궤도 추적 제어 시스템을 설계하였고, 시뮬레이션을 통하여 제안한 방법의 우수성을 증명하였다.
본 논문에서는 이동로봇에 외란이 가해지더라도 외란이 없는 경우의 PDC 제어 기법에 의한 궤도 추적 성능을 유지하도록 하는 강인한 궤도 추적 방법을 제안하였다. 비선형 시스템인 이동로봇의 주행 궤도와 기준궤도 간의 에러 동특성 방정식을 T-S 퍼지 모델링 한 후 Lyapunov 안정 조건 및 LMI 연산을 이용해 상태 궤환이득을 구하여 공칭 제어 입력을 얻었고, ISMC 기법을 적용하여 외란이 있는 경우에도 공칭계통의 동특성을 유지할 수 있도록 하는 불연속 제어 입력을 얻었다. 이 두 제어 입력을 더하여 이동로봇에 인가함으로써 외란에 강인한 궤도 추적 성능을 얻을 수 있었다.